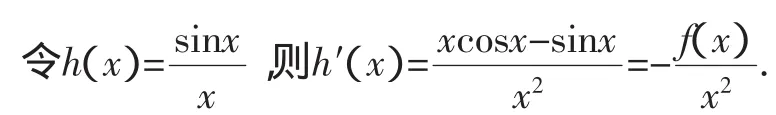三角函数背景下导数命题赏析
2016-11-19江苏省南通第一中学葛小萍
☉江苏省南通第一中学葛小萍
三角函数背景下导数命题赏析
☉江苏省南通第一中学葛小萍
以三角函数为背景综合考查导数的应用是近年高考命题的一个新的亮点,问题的求解中除了导数的基本运算外,还要充分结合三角函数的基本性质和运算.下面引例说明.

解析:有关比较大小问题,通常转化为判断函数的单调性来处理,而导数又是判断函数单调性的有利工具.因为条件中所要判断的三个函数值均在内,结合函数的奇偶性(易判断函数f(x)为偶函数),因此进一步判断函数f(x)=xsinx在)内的单调性即可.求导得f′(x)=sinx+xcosx,当x∈f′(x)>0,所以f(x)为增函数.由函数f(x)为偶函数知f(-1)=f(1)
答案A.
评析:对于x与sinx的组合函数,除了本例所述形式外,还有的形式(见后面变式),处理相关问题时要注意x与sinx的关系,如当x>0时,有sinx
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)求集合A={x|f(x)=0}中元素的个数.
解析:(1)函数f(x)是偶函数,证明如下:
因为f(-x)=acos(-x)-xsin(-x)=acosx+xsinx=f(x),
所以f(x)是偶函数.
(2)当a>0时,因为f(x)=acosx+xsinx>0恒成立,所以集合A={x|f(x)=0}中元素的个数为0.
所以集合A={x|f(x)=0}中元素的个数为1.
当a<0时,因为f′(x)=-asinx+sinx+xcosx=(1-a)sinx+
由f(x)是偶函数可知,集合A={x|f(x)=0}中元素的个数为2.
综上所述,当a>0时,集合A={x|f(x)=0}中元素的个数为0;当a=0时,集合A={x|f(x)=0}中元素的个数为1;当a<0时,集合A={x|f(x)=0}中元素的个数为2.
评析:本题函数奇偶性与单调性的判断与引例如出一辙.对于零点个数问题的常规处理策略是将其转化为函数图像与x轴交点个数问题,再利用导数来判断函数的单调性、求极值最值来处理.此处若一开始就直接对函数进行求导,那么对于当a>0时,f′(x)=(1-a)sinx+xcosx的x∈内的正负符号不易判断,导致解题无法进行.因此在处理相关问题时切忌直接求导,应先根据参数的不同取值范围,直接来判断原函数的零点情况,即当a=0与a>0时,根据零点问题相关知识可直接判断,当a<0时,无法直接判断时,再利用导数进一步求解.
(1)求证:f(x)≤0;
g′(x)=cosx-c.
当c≤0时,g(x)=sinx-cx>0恒成立.
当c≥1时,g′(x)=cosx-c<0,此时g(x)=sinx-cx在)上是减函数,
g(x) 当0 当x∈(0,x0)时,g′(x)>0; 所以g(x)=sinx-cx在区间(0,x0)上单调递增,在区间上单调递减. 当c≥1时,g(x)<0. 评析:第(1)问证明f(x)≤0,即函数的最大值小于等于0,利用导数即可简捷求解.第(2)问与引例相比,将的形式体现出来.若令,则g′(x)=,其中分子就是第(1)问中的f(x),由(1)知g′(x)<0对x∈)恒成立,则g(x)在)上是单调递减函数,所以,a的最大值是但是在利用同种方法处理时,陷入困境.注意到在恒成立,等价于,因此只需研究函数y= sinx-bx和y=sinx-ax,的最值情况.由于这两个函数在形式上一致,故可构造一个新函数g(x)=sinxcx,c为常数,再利用导数法研究新函数的最值即可. 变式3已知函数f(x)=sinx-xcosx. (1)求曲线y=f(x)在点(π,f(π))处的切线方程; 解析:f′(x)=cosx-(cosx-xsinx)=xsinx. (1)因为f′(π)=0,f(π)=π,所以切线方程为y=π. 则g′(x)=xsinx-x2=x(sinx-x). 评析:本题在第(2)问求解中,利用了二次求导法,即当导函数正负不易判断时,可将导函数或其中的一部分视为新的函数,再次求导来判断.对于第(3)问分离出参数k后,不难发现它就是变式2第(2)问的部分.因此可借助变式2点评中所述的方法求解.另外如果是客观题,我们也可以借助函数的几何意义,即将f(x)=视为y=sinx图象上的点(x,sinx)与坐标原点连线的斜率,结合函数图像易知当点(x,sinx)与坐标原点重合时,即在点(0,0)处直线变为切线,此时斜率最大且最大值为1;当点(x,sinx)为)直线的斜率最小且最小值为,从而使问题简捷获解.