热方程边界值决定反问题的数值方法
2016-11-19陈风雷马正义
陈风雷,马正义,2
(1.浙江理工大学理学院,杭州 310018;2.丽水学院工程与设计学院,浙江丽水 323000)
热方程边界值决定反问题的数值方法
陈风雷1,马正义1,2
(1.浙江理工大学理学院,杭州 310018;2.丽水学院工程与设计学院,浙江丽水 323000)
给出了求解热方程边界值决定反问题的直接差分法和配置法两种数值算法。直接差分法采用Euler向后差分格式;配置法把反问题化为拟解问题,利用Lagrange插值基函数构造有限维逼近,从而将问题转化为求解一个代数方程组,最后采用正则化方法求解。数值结果表明:直接差分法的反演结果在区间的左端有较强的振荡,而配置法能够整体恢复左边界值,并且配置法可灵活选择正问题的数值格式获得较高的精度。
边界值决定反问题;直接差分法;配置法;正则化; Lagrange插值
0 引 言
自然科学与工程技术上的许多问题都可以归结为反问题,其中一类重要的反问题称为边界值决定反问题,即由可接触的边界或容易接触的边界(值)的信息决定不可接触或不易接触的边界(值)的信息。例如,织物外侧的温度和湿度容易测量,但织物与人体之间的温度不易测量。类似的例子还有无损检测、高炉炼铁等,甚至地震预测也可以归为这类问题[1-2]。
本文研究热方程的边界值决定反问题。该问题是不适定的,输入数据的微小误差可能导致数值解的巨大变化,因此需要采用正则化技巧给出稳定的数值方法[3]。目前已有不少这方面的工作,主要可以归为两类方法:差分法和Fourier变换方法。
对于差分法,Murio[3]提出了完全显示且稳定的空间差分推进格式。利用具有平均核的离散卷积过滤噪声数据,Murio把该类反问题转化为一个适定性问题,然后使用空间推进的差分格式求解。Elden[4]研究了时间差分推进格式的正则化效应,发现时间差分可以防止解在高频部分发生爆破,即时间方向的差分具有正则化效应。
另外一类为Fourier变换方法,该方法把偏微分方程从空间域转化到频率域,从而获得复变量的常微分方程。对该常微分方程,Hao[5]给出了Fourier逆变换下的显示解,发现反问题不稳定正是高频部分造成的。对显示解的不同处理可获得不同的数值方法,如Fourier正则化方法、谱正则化方法、Tikhonov法、小波方法和最优过滤法等[6-9],这些方法统称为Fourier变换方法。
以上两类方法各有优缺点。差分方法简单,容易实施,但对复杂方程很难给出误差估计,而且不同差分格式的结果往往呈现较大差异。Fourier变换方法对空间变量进行Fourier变换,这要求方程系数仅依赖于空间变量,尤其对非线性问题,Fourier变换难以实施,这限制了Fourier变换方法的适用范围。
Hasanov等[10]用配置法求解了一类反问题,即时间后向的抛物型问题(backward parabolic problems,BPP),获得了稳定且较高精度的数值解。本文将配置法用于求解热方程边界值决定反问题。配置法是对原问题的有限维逼近,通过对反演函数进行插值,将反问题转化为一系列以插值基函数为输入数据的正问题和一个不适定的代数方程组,而正问题是稳定的,因此配置法可以有效地抑制反问题的不稳定性。本文给出了直接差分法和配置法的数值结果,并对两种方法进行了比较。
1 热方程边界值决定反问题
热方程边界值决定反问题可用下面一般的方程表示:
(1)
其中:u∈C2,1((0,1)×(0,T))为温度;κ(x,t)∈C1,0((0,1)×(0,T))表示热传导率;Θ(x,t)表示源项(辐射项和蒸发冷凝项);v(x,t)为初始条件;φ(t),Q(t)表示该方程边界条件; T表示时间变量的上界。反问题的目的是通过求解问题(1)来决定左边界值u(0,t)。本文称问题(1)为IP(inverse problems)。
上述反问题可等价描述为求解P(t),使得满足方程组:
(2)
且
(3)
易知,对于可测量数据:初边值、热传导率κ(x,t)和源项Θ(x,t),若初边值发生变化时,若问题(2)的解并不是线性依赖于左边界值P(t)的解,但可以通过如下处理进行线性化。令u=w+z,其中w、z分别满足:
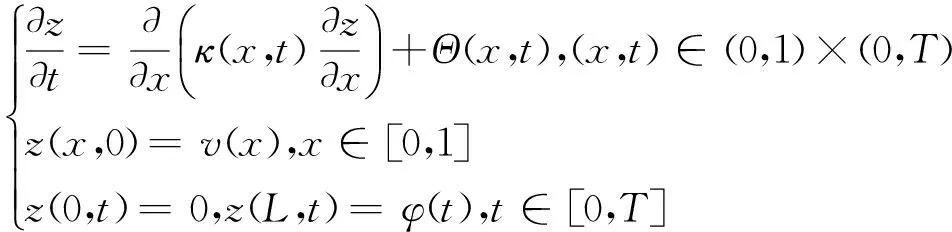
显然w关于P(t)是线性的,而z可以直接求解。
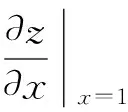
则反问题归结为求算子方程
f(P)=0
的零点。可考虑最小二乘解,即求如下泛函的极小元:
F:L2[0,T]→[0,+∞),
(4)
以上优化问题的解称为IP的拟解。
2 数值算法
本节考虑IP的数值算法,即直接差分法和配置法。
2.1 直接差分法
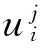
(5)
令s=τ/h2,式(5)可等价如下线性方程组:
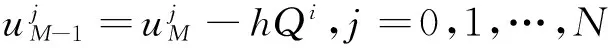
即:
(6)
其中:
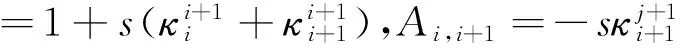
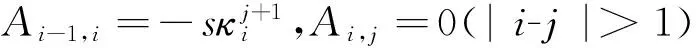
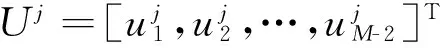
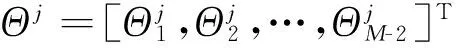
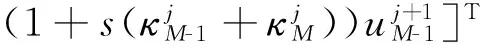
2.2 配置法
用配置法求解(4)的算法如下:
Step 1 用Lagrange基函数对边界值P(t)进行插值,即:
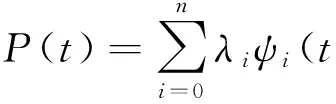
由于所考虑的问题是线性的,因此有:
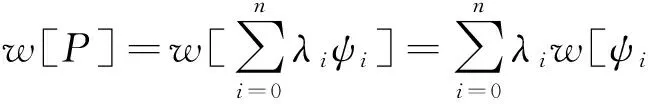
Step 2 泛函(4)可写为
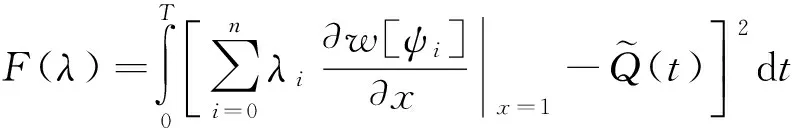
由极值的必要性:

从而有线性方程组
Aλ=b
(7)
其中A=(aij),b=(b0,b1,…,bn)T,而

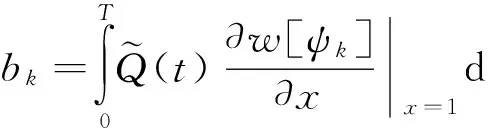

Step 4 如果矩阵A的条件数较大,则采用正则化方法求解,如广义交叉校验Tikhonov正则化法、广义交叉校验TSVD正则化法[11-13],否则直接用最速下降法[14]求解。
3 数值模拟
算例1:考虑如下问题:
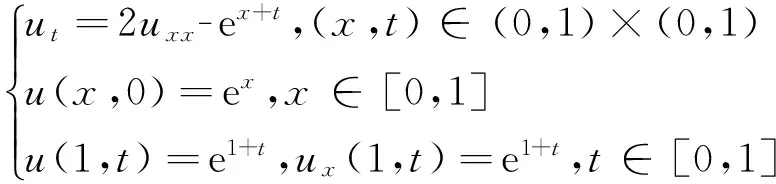
易知该问题有唯一解u(x,t)=ex+t,从而u(0,t)=et。
a)直接差分法的数值结果
取步长τ=1/100,h=1/200,直接差分法的数值解与精确解见图1和图2。
从图1和图2中可以得出,左边界值在区间的左侧具有明显的振荡,为此进行截断,见图3。

(a)精确解
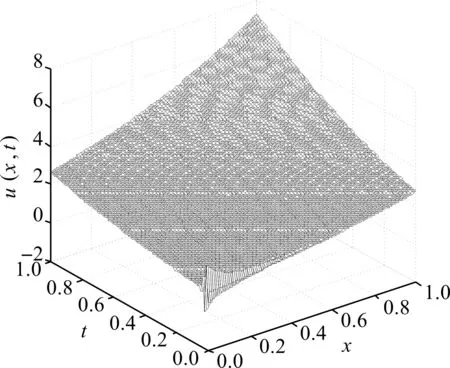
(b)数值解图1 u(x,t)精确解与数值解
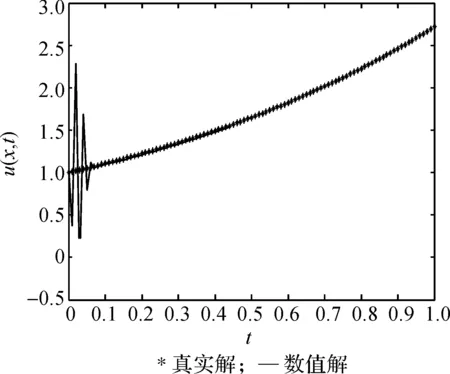
图2 u(0,t)数值解与精确解
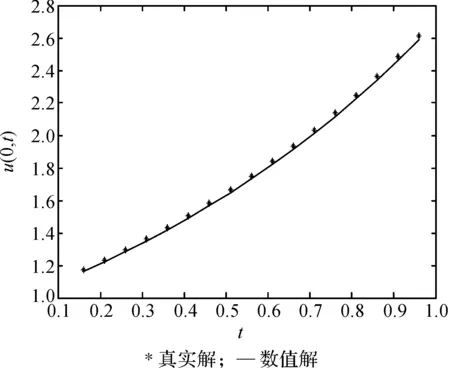
图3 u(0,t)截断后的数值解与精确解
图3表明,截断后的图像与精确解吻合。在实际运用中,若考虑长时间后的扩散或传递行为,差分法不论在计算时间上还是数值精度上都满足工业要求。
b)配置法的数值结果
取Lagrange基函数的阶n=5,反问题离散为N=100,M=200,计算(7)时矩阵A的条件数为1.594×104,可直接采用最速下降法求解。
对右边界u(L,T)数据在不同噪声水平下,u(0,t)数值解与精确解如图4所示。
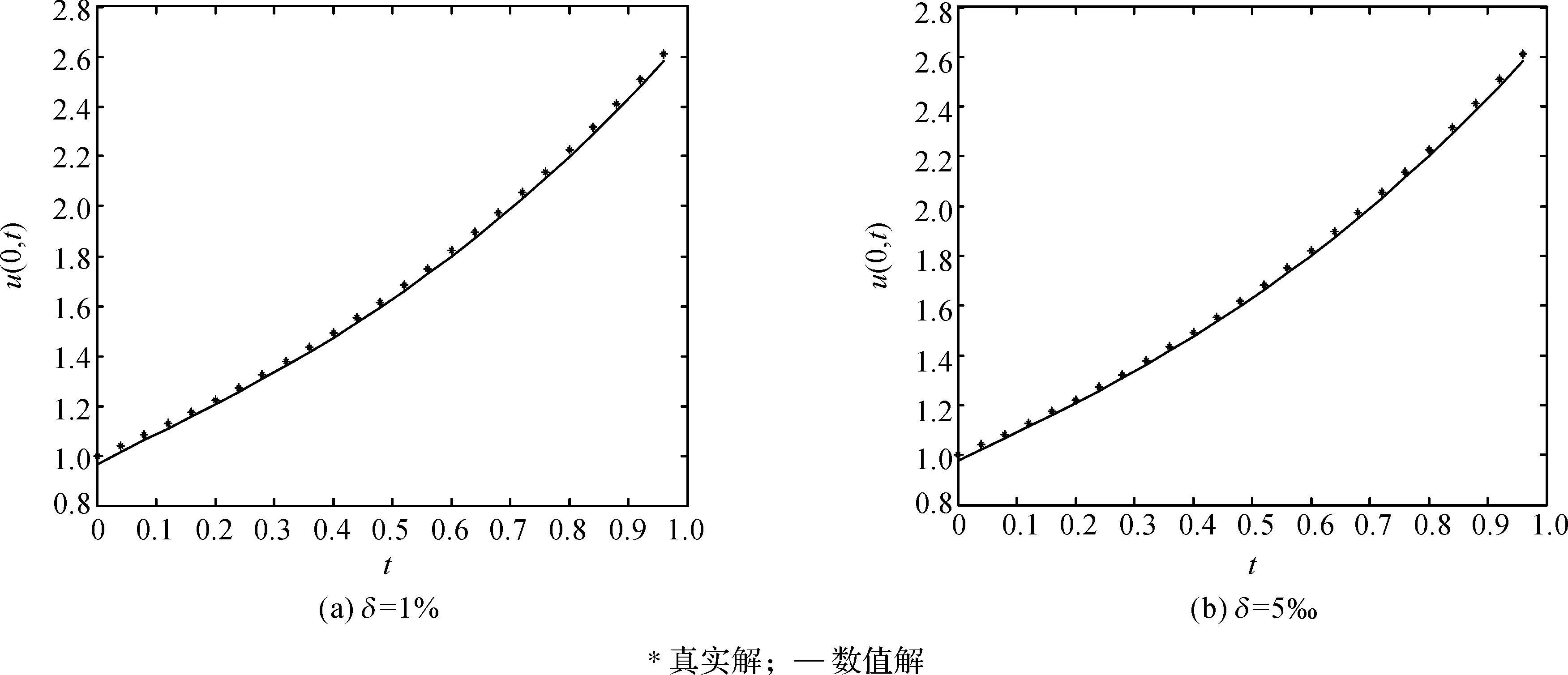
图4 不同噪声δ下u(0,t)数值解与精确解
图4表明:配置法的反演结果并没有产生振荡,且具有较高的精度,因此对整体反演结果,配置法比较合适。

表1 配置法误差结果
通过不同阶的Lagrange基函数进行数值计算,结果如图5所示。
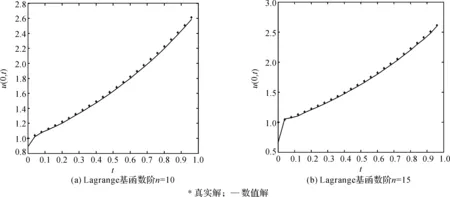
图5 噪声δ=1%时u(0,t)的数值解与精确解
从图5(a)可以发现数值解误差比较小,但在提高Lagrange基函数的阶数为15时(见图5(b)),计算精度并没有因为阶的增大而提高,这可能是高次插值的龙格现象[14]。为此可尝试采用Chebyshev多项式的零点作为插值节点以避免龙格现象,数值结果如图6所示。从图6中可以发现,在端点处同样出现较大误差,这是算法本身的原因。事实上,对以每个基函数为左边界值的正问题,误差在原点附近都是最大,因此误差是由正问题的数值算法导致的。

图6 噪声δ=1%时u(0,t)的数值解和精确解
算例2 考虑如下方程:

已知上述方程精确解:u(x,t)=exsint,从而初始条件为:u(0,t)=sint.
a)差分法的数值结果
取步长为τ=1/100,h=1/400边界u(0,t)数值解与精确解如图7所示。
图7中同样发现:在若干个时刻的数值结果有明显的振荡,并且在振荡后数值解与真实解非常接近。
b)配置法的数值结果
取Lagrange基函数的次数n=5,反问题空间离散取N=100,M=200,计算(7)时其矩阵的条件数为86.3437,直接采用最速下降法。
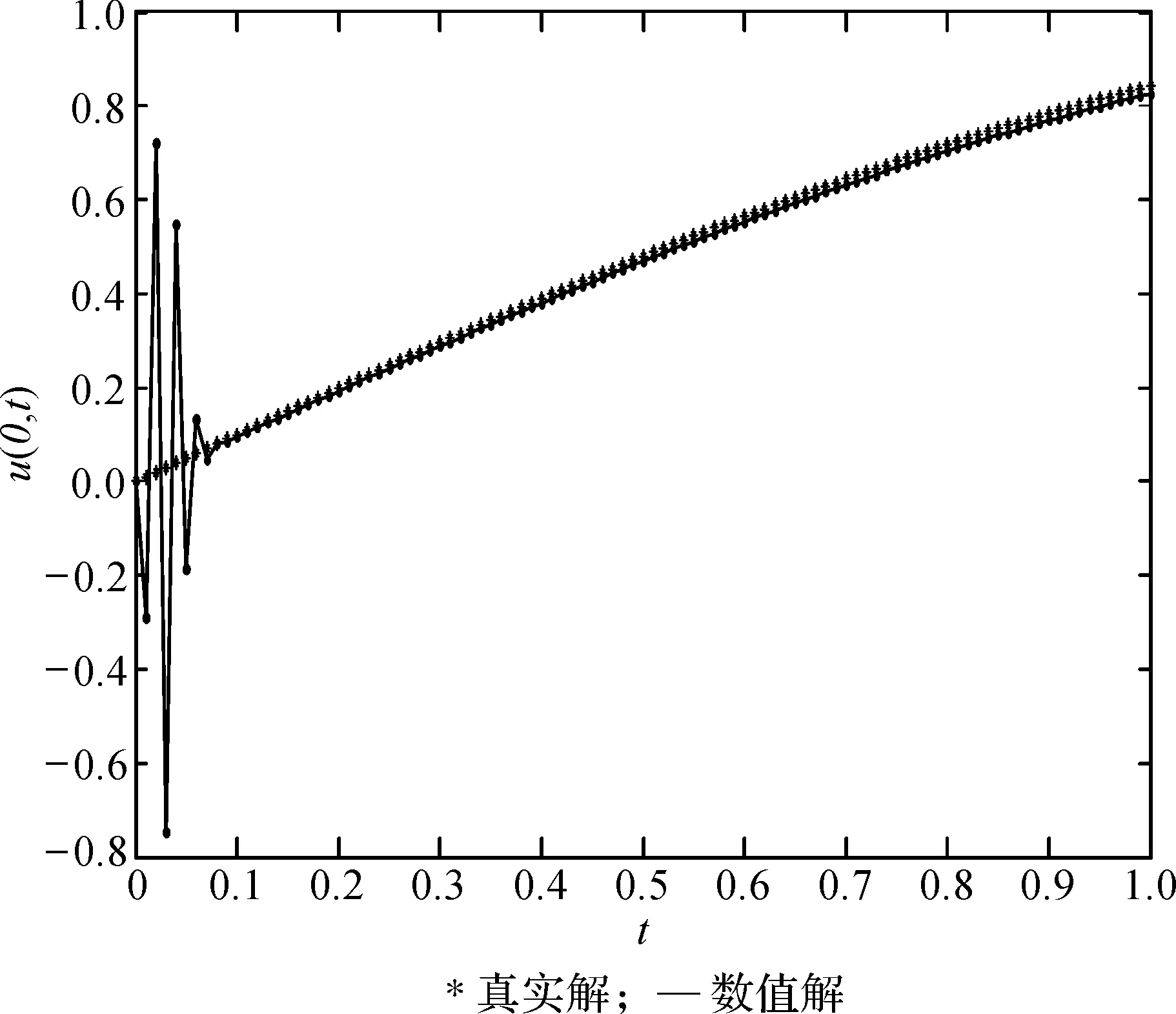
图7 u(0,t)数值解与精确解
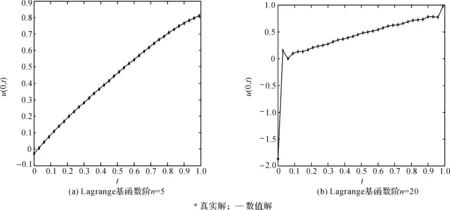
图8 噪声δ=0.01时u(0,t)数值解与真实解
从图8可以看出,配置法克服了直接差分法在起始时刻产生的较强的振荡,从而获得整个区间上的稳定解。
4 结 论
本文采用直接差分法和配置法研究了一类热方程边界值决定反问题,并给出相关数值计算。直接差分法只需简单迭代,用时短,但数值结果表明,直接差分法在区间左端具有明显的振荡。因此,若考虑长时间后的扩散或传递行为,直接差分法在时间损耗和数值精度上都能满足工业要求。配置法把反问题转化为一系列的正问题,通过灵活选取正问题的数值格式,不仅能够获得较高的精度,而且对于初边值在不同的噪声水平下都可以避免较强的振荡。但是配置法需要求解大量正问题,为此可采用并行计算缩短计算时间。综上分析,配置法对热方程边界值决定反问题比直接差分法具有更强的适用性。
[1] 徐定华.纺织材料热湿传递数学模型及设计反问题[M].北京:科学出版社,2014:1-12.
[2] 戴会超,王玲玲.工程水力学反问题研究及应用[J].四川大学学报,2006,38(1):15-19.
[3] MURIO D A. The mollification method and the numerical solution of the inverse heat conduction problem by finite differences [J]. Computers & Mathematics with Applications,1989,17(10):1385-1396.
[4] ELDEN L. Numerical solution of the sideways heat equation bydifference approximation in time [J]. Inverse Problem,1995,11(4):913-923.
[5]HAO D N. On a sideways parabolic equation[J]. Inverse Problems,1998,13(2):297-309.
[6] CARASSO A. Determining surface temperatures from interior observations[J]. SIAM JAppl Math,1982,42(3):558-574.
[7] CHOUDHURYAH. Wavelet Method for Numerical Solution of Parabolic Equations[J/OL]. Journal of Computational Engineering,2014:1-12.http://dx.doi.org/10.1155/2014/346731.
[8] SEIDMAN T I,ELDEN L. An optimal filtering method for the sideways heat equation[J].Inverse Problems,1990,6(4):681-696.
[9] TAUTENHAHN U. Optimal stable approximations for the sideways heat equation[J]. Inverse Ill-Posed Problems,1997,5(3):287-307.
[10] HASANOVA,MUELLER J L .A numerical method for backward parabolic problems with non-self adjoint elliptic operators[J].Applied Numerical Mathematics,2001,37(1/2):55-78.
[11] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005:46-55.
[12] 韩波,李莉.非线性不适定问题的求解方法及应用[M].北京:科学出版社,2011:25-118.
[13] HANSEN PC. The truncated SVD as a method for regularization [J]. Bit Numerical Mathematics,2010,27(4):534-553.
[14] 李庆扬,王能超,易大义.数值分析[M].北京:清华大学出版社,2012:202-204.
(责任编辑: 康 锋)
Numerical Methods of Inverse Problem of Boundary Value Determination of Heat Equation
CHENFenglei1,MAZhengyi1,2
(1.School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China; 2.Institute of Engineering and Design, Zhejiang Lishui University, Lishui 323000, China)
In this paper, a direct difference method and a collocation method are applied to solve an inverse problem of boundary value determination of heat equation. The direct difference method adopts the Euler backward difference scheme. The collocation method first formulates the inverse problem to a quasi-solution problem and then uses base function of Lagrange interpolation to construct finite dimension approximation. In this way, the original problem is turned into solution of a system of algebraic equations. Finally, regularization method is used to solve. Numerical result shows that the inversion result of direct difference method presents strong fluctuation at the left end of interval, while the collocation method can recover the left boundary value on the whole and is easy to obtain higher precision by choosing appropriate numerical format of the direct problem.
inverse problem of boundary value determination; direct difference method; collocation method; regularization; Lagrange interpolation
10.3969/j.issn.1673-3851.2016.11.025
2016-04-16
国家自然科学基金项目(11071221);浙江省自然科学基金项目(LY14A010005)
陈风雷(1990-),男,安徽淮北人,硕士研究生,主要从事数理方程的反问题方面的研究。
马正义,E-mail:ma-zhengyi@163.com
O241.5; O241.82
A
1673- 3851 (2016) 06- 0945- 06 引用页码: 110802
