OST方程初值问题的低正则性
2016-11-18贾红艳王宏伟
贾红艳,王宏伟
(安阳师范学院 数学与统计学院,河南 安阳 455002)
OST方程初值问题的低正则性
贾红艳,王宏伟
(安阳师范学院 数学与统计学院,河南 安阳 455002)
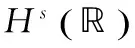
OST方程;初值问题;低正则性
笔者将研究如下一类OST方程的初值问题,它是Ostrovsky等[1]在研究非线性长波的辐射不稳定性问题时建立的数学模型
(1)
其中:u=u(x,t)是未知函数,H表示Hilbert变换
OST方程是一类具有扰动项的KdV方程.许多学者对这种方程进行了研究,得到了大量的研究成果[2-8].各种非线性项的OST方程初值问题的适定性,也受到了广泛关注.如Alvarez[9]在Hs()(s>1/2)和(s≥1)中分别证明了具有平方非线性OST方程初值问题局部解和整体解的适定性.Zhao[10-11]利用Bougain空间中的双线性估计在(s>-5/4) 中证明了局部解的适定性.对具有3次非线性项的OST方程,Carvajal[12]在(s≥0)中证明了初值问题局部解的适定性.对非线性是2的OST方程的初值问题,目前还没有相关结果.笔者将利用Carvajal[13]的方法研究具有非线性项2的OST 方程的初值问题.通过构造一类新的辅助空间,利用中的先验估计,在索伯列夫空间(s>-1/2)中证明了局部解的适定性.主要结论如下:
定理1 如果s>-1/2,那么对任意的φ∈Hs(),存在,使得方程(1)有唯一解u(t)满足.另外,方程的解映射
是光滑的,且
(2)
1 先验估计
引理1 如果a>0,b<0,f(t)=taetb,那么对任意的t≥0,有
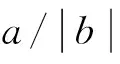
引理2 如果0 即 引理3 如果0 (3) 证明 首先估计‖V(t)φ‖Hs,有 利用引理2,得到 注意到 即I2≤C.引理3得到证明. 引理4 如果-1/2 (4) (5) (6) (7) (8) 合并(7),(8)两式有 (9) 把(6)和(9)式代入(5)式中,得到 作变量替换t′=tτ,有 根据a的定义和s的范围,上式右端项的积分是有限数,有 (10) (11) 类似(9)式,可以估计 (12) 把(6),(11)式代入(10)式,得 (13) 作变量替换t′=tτ,利用上式,有 上式右端的欧拉积分是有限的,于是 (14) 合并(10)和(14)式,引理得到证明. 是从[0,T]到Hs+μ的连续映射. 应用Lebesgue控制收敛定理,当t→t0时,I1(t,t0)→0.类似地, 故当t→t0时,I2(t,t0)→0.引理证毕. 定理1的证明:如果s>-1/2,φ∈Hs(),0 定义一个映射 定理得到证明. [1] OSTROVSKY L A,STEPANYAMS Y A,TSIMRING L S.Radiation instability in a stratified shear flow[J].Int J Non-Linear Mech,1984,19:151-161. [2] MOLINER L,RIBAUD F.The Cauchy problem for dissipative Korteweg-de Vries equations in Sobolev spaces of negative order[J].Indiana Univ Math J,2001,50:1745-1776. [3] MOLINET L,RIBAUD F.The global Cauchy problem in Bourgain type spaces for a dispersive dissipative semilinear equation[J].SIAM J Math Anal,2002,33:1269-1296. [4] MOLINET L,RIBAUD F.On the low regularity of the Kortewef-de Vries-Burgers equation[J].Int Math Res Not,2002,37:1979-2005. [5] DIX D B,Nonuniqueness and uniqueness in the initial-value problem for Burgers equation[J].SIAM J Math Anal,1996,27:708-724. [6] GUO Z,WANG B.Global well-posedness and inviscid limit for the Korteweg-de Vries-Burgers equation[J].J Diff Equa,2009,246:3864-3901. [7] CHEN W,LI J.On the low regularity of the modifiedKorteweg-de Vries equation with a dissipative term[J].J Diff Equa,2007,240:125-144. [8] KENIG C E,PONCE G,VEGA L.Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle[J].Comm Pure Appl Math,1993,46:527-620. [9] ALVAREZ B.The Cauchy problem for a nonlocal perturbation of the KdV equation[J].Differential Integral Equations,2003,16 (10):1249-1280. [10] ZHAO X.On low regularity of the Ostrovsky,Stepanyams and Tsimring equation[J].J Math Anal Appl,2011,378:687-699. [11] ZHAO X,CUI S.Local well-posedness of the Ostrovsky Stepanyams and Tsinmring eqution in Sobolev spaces of negative indices[J].Nonliner Anal,2009,70:3843-3510 [12] CARVAJAL X,SCIALOM M.On the well-posedness for the generalized Ostrovsky,Stepanyams and Tsimring equation[J].Nonlinear Anal,2005,62:1277-1287. [13] CARVAJAL X,PANTHEE M.On the well-posedness of higher order viscous Burgers equations[J].J Math Anal Appl,2014,417:1-22. (责任编辑 朱夜明) On low regularity for initial value problem of OST equation JIA Hongyan,WANG Hongwei (School of Mathematics and Statistics,Anyang Normal University,Anyang 455002,China) OST equation;initial value problem;low regularity 10.3969/j.issn.1000-2162.2016.06.003 2015-02-05 国家自然科学基金资助项目(10771166);河南省教育厅科学技术研究重点项目(14B110028,16A110007);安阳师范学院科研培育基金资助项目(AYNU-KP-B04) 贾红艳(1981-),女,河南安阳人,安阳师范学院讲师. O175 A 1000-2162(2016)06-0010-05
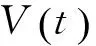

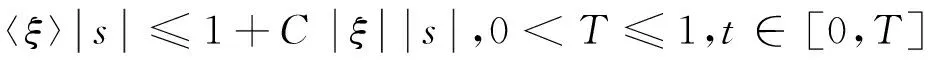

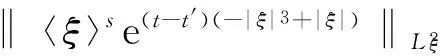
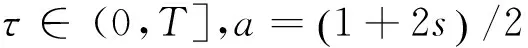

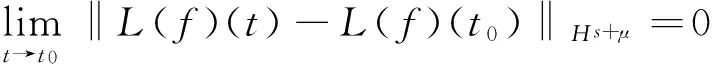

2 主要定理的证明





