吡啶基离子液体[C6py][DCA]热力学性质及利用新Eötvös方程预测其表面张力
2016-11-18卜晓雪樊本汉魏杰邢楠楠2马晓雪关
卜晓雪樊本汉魏 杰邢楠楠,2马晓雪关 伟,*
(1辽宁大学化学院,沈阳 110036;2黄山学院化学化工学院,安徽 黄山 245041)
吡啶基离子液体[C6py][DCA]热力学性质及利用新Eötvös方程预测其表面张力
卜晓雪1樊本汉1魏 杰1邢楠楠1,2马晓雪1关 伟1,*
(1辽宁大学化学院,沈阳 110036;2黄山学院化学化工学院,安徽 黄山 245041)
制备了吡啶类离子液体N-己基吡啶二氰胺盐[C6py][DCA],并用核磁共振氢谱(1H NMR)、核磁共振碳谱(13C NMR)、差热扫描量热(DSC)、傅里叶变换红外(FT-IR)光谱对其进行表征。在288.15–338.15 K温度范围内,采用标准加入法,测定其密度(ρ)、表面张力(γ)和折光率(nD)。在测得的实验数据的基础上,得到了离子液体[C6py][DCA]的分子体积(Vm)、表面能(Ea)、摩尔极化度(Rm)和极化率(αp)。结果显示Ea、Rm和αp几乎不随温度的变化而发生改变。本文还提出了摩尔表面Gibbs自由能(gs)的概念,并改进了Eötνös方程。同时还计算了gs、临界温度(Tc)和Eötνös方程经验参数(kE),并预测了离子液体[C6py][DCA]的表面张力,预测值与实验值具有较好的一致性。
吡啶基离子液体;密度;表面张力;摩尔表面Gibbs自由能;Eötνös方程
1 引 言
近年来,离子液体(ILs)因其独特的物理化学性质如蒸气压小、热容大、导热性高、热稳定性好、液态温度宽等而备受关注1。这些性质使离子液体在制药、物理和化学等诸多领域有着广阔的应用前景2–6。其中,吡啶基离子液体除了具有咪唑基离子液体的特性外,还具有热稳定性好、热容高、毒性低及价格更加低廉等特点7–10,这就使得其在环境科学等研究领域得到了更多的关注11–14。同时,含有二氰胺阴离子的离子液体可以用作新型自燃材料和推进剂等15,16。
在工业生产中,离子液体物理化学性质的基础数据可以指导设备选型或工艺设计,因而十分重要。由于离子液体具有“可设计”性,故合成并测定所有离子液体的相关性质的基础数据是一项几乎不可能实现的工程。如果能够预测所需离子液体的物理化学性质,并使其相关特性能够满足需求,就显得很重要了。近年来,运用估算和预测的方法研究物质的物理化学性质已成为一种发展趋势,尤其是在用半经验方法研究离子液体的相关性质方面17–20。
作为本课题组前期工作21–25的延续,本文报道了如下工作:(1) 制备了N-己基吡啶二氰胺盐离子液体[C6py][DCA];(2) 在288.15–338.15 K,运用标准加入法(SAM)21,25,26,测定离子液体[C6py][DCA]的密度(ρ),表面张力(γ)和折光率(nD);(3) 计算了离子液体[C6py][DCA]的分子体积(Vm)、表面能(Ea)、摩尔极化度(Rm)和极化率(αp),并讨论了这些性质与温度的关系;(4) 提出了摩尔表面Gibbs自由能(gs)的概念,改进了Eötvös方程,并预测了离子液体[C6py][DCA]的表面张力;(5) 计算了gs,临界温度(Tc)和Eötvös方程经验参数(kE)。
2 实验部分
2.1 实验药品
吡啶(> 99.9%)、1-溴代己烷(> 99.9%)、二氰胺钠(> 99%)、硝酸银(> 99%)、乙酸乙酯(> 99.9%)均购自于化学试剂国药控股有限公司。
2.2 [C6py][DCA]的制备
根据文献25,27,28方法,将等体积比的吡啶和乙酸乙酯置于斜三口球瓶中,再将适量的1-溴代己烷置于恒压分液漏斗中。恒温至301.15 K后,向体系中滴加1-溴代己烷,反应72 h。反应结束后,加入乙酸乙酯并搅拌,重结晶,直至生成白色颗粒,真空干燥48 h。所得产物即为中间体[C6py][Br],密封保存。
称取一定量的AgNO3和NaDCA溶解水中,将二氰胺钠溶液置于恒压分液漏斗中,并滴加至硝酸银溶液中。滴加完成后,静置、分层、抽滤,得到白色沉淀中间体AgDCA待用。将一定量的[C6py][Br]溶于水中置于斜三口球瓶中,加入上述得到的白色中间体AgDCA,搅拌24 h。反应结束后,抽滤、旋蒸,得到淡黄色离子液体[C6py][DCA],干燥24 h。
对合成产物进行1H NMR、13C NMR、DSC、FT-IR (见Supporting Information的图S1–S4及表S1–S2)。经核磁共振谱分析没有发现杂质共振峰。对DSC谱图分析,[C6py][DCA]的玻璃化转变温度Tg为–82.74 °C。目标产物[C6py][DCA]的纯度(HPCL/质量分数)为99.02%(见图S5)。
2.3 [C6py][DCA]密度、表面张力和折光率的测定
考虑到N-烷基-吡啶二氰胺离子液体[C6py][DCA]与水能够形成很强的氢键29,使得用常规的方法很难除尽其中的微量水,这会对离子液体ρ、γ和nD的测定产生影响。故采用标准加入法(SAM)来消除这种影响。用SFY-3000型微量水分测定仪对[C6py][DCA]的含水量w2(质量分数)进行测定,根据SAM,配置一系列不同含水量的[C6py][DCA]样品。
本文使用安东帕DMA 4500密度计在288.15– 338.15 K下测定具有不同含水量的离子液体[C6py][DCA]的密度,测量精确度为±0.00005g·cm–3,控温精确度为±0.03 K。测定前对仪器进行校正,校正值与其文献值30基本一致,实验误差为±0.00001 g·cm–3。测定时,样品在每个温度下测定三次,取平均值列于表S3。将测定温度下的密度值对含水量作图(见图S6),能够得到拟合标准偏差在实验误差范围内,相关系数大于0.99的直线,直线的截距为纯离子液体的密度,相关数据均列于表S3中。
本文使用南京桑力DP-AW表面张力实验装置测定离子液体[C6py][DCA]的表面张力,测量精确度为±0.2 mJ·m–2。测定前,对仪器进行校正,校正值与文献值30基本一致。在288.15–338.15 K下,分别测定一系列不同含水量的[C6py][DCA]的表面张力。升温时,待温度达到预设值后恒温30 min再开始读数。测定三次,取平均值列于表S4。将相应温度下测得的表面张力对含水量作图(见图S7),能得到很好的直线,拟合系数大于0.99,拟合标准偏差在实验误差范围内,截距为纯离子液体[C6py][DCA]的表面张力,相关数据列于表S4。
在288.15–338.15 K下,使用WYA-2W双目阿贝折光仪测定离子液体[C6py][DCA]的折光率,测量精确度为±0.0002。实验前对仪器进行校正,实验误差为±0.0001。测定时,待温度升至预设值后恒温30 min再读数。测定三次,取平均值,列于表S5中。将指定温度下测得的折光率对含水量作图(见图S8),能得到拟合系数大于0.99的直线,拟合标准偏差在实验误差范围内,截距为无水离子液体[C6py][DCA]的折光率,相关数据列于表S5中。
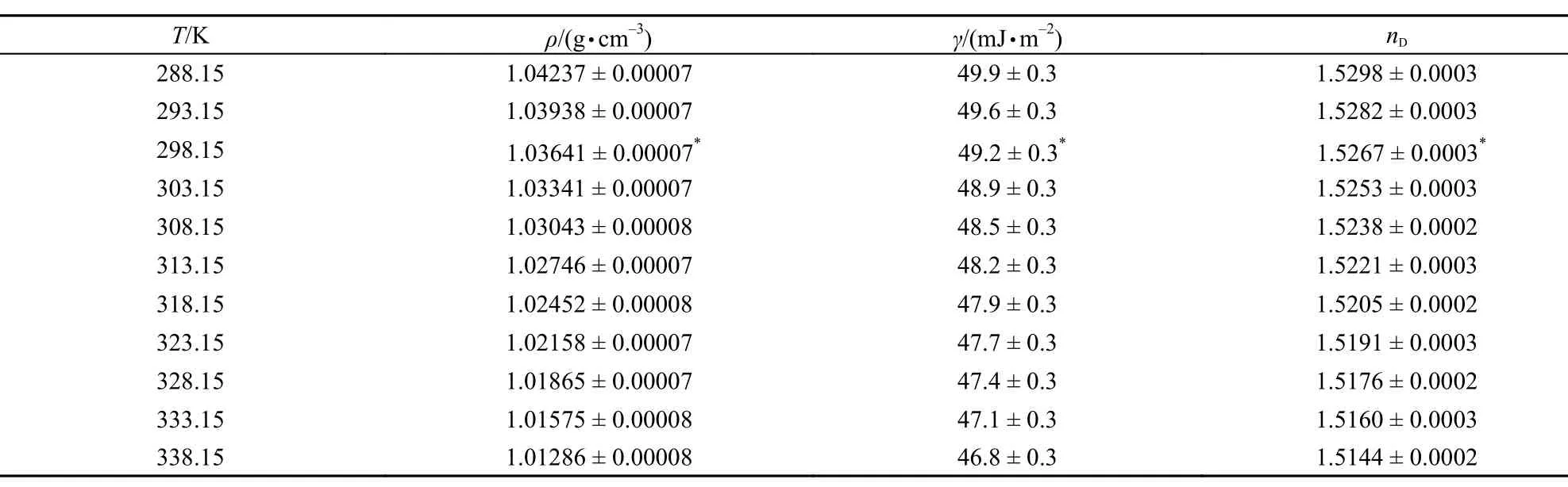
表1 在 288.15-338.15 K、0.1 MPa下, [C6py][DCA]的ρ、γ和nDTable 1 Density (ρ), surface tension (γ), and refractive index (nD) for [C6py][DCA] at the temperature range from 288.5 to 338.15 K and pressure of 0.1 MPa

表2 288.15 - 338.15 K, [C6py][DCA]的Vm、Ea、Rm和αpTable 2 Molecular volume (Vm), energy of surface (Ea), molar refraction (Rm), and polarization coefficient (αp) for[C6py][DCA] from 288.15 to 338.15 K
3 结果与讨论
3.1 [C6py][DCA]密度、表面张力和折光率
根据SAM,测定不同含水量[C6py][DCA]的ρ、γ和nD,通过线性回归外推得到纯离子液体,即不含水的离子液体的ρ、γ和nD值。其值及其在0.95置信水平的实验扩展不确定度列于表1。
从表1中可以看出,随着温度的升高,离子液体[C6py][DCA]的ρ、γ及nD值均减小。
3.2 [C6py][DCA]的体积性质
根据上文测得的离子液体[C6py][DCA]的ρ,可以得到其分子体积Vm(阴、阳离子体积之和)31,计算公式如下:

式中M是离子液体的摩尔质量,N是Avogadro常数。根据公式(1)可计算出[C6py][DCA]的Vm,并将计算结果列于表2中。为了讨论其与温度的关系,以Vm为Y轴,温度(T)为X轴作图(见图1),线性拟合得到一条斜率非常小的直线,这说明Vm随着T的升高而略微增大。

图1 288.15-338.15 K, [C6py][DCA]的Vm对T作图Fig.1 Plot of Vmvs T of ILs [C6py][DCA] at the temperature range from 288.15 to 338.15 K
3.3 [C6py][DCA]的表面性质
根据最小二乘法线性经验方程, 将利用SAM得到纯离子液体[C6py][DCA]的γ值对T作图(见图2),拟合得到如下方程:


图2 288.15-338.15 K, [C6py][DCA]的γ对T作图Fig.2 Plot of γ vs T of ILs [C6py][DCA] at the temperature range from 288.15 to 338.15 K
式中A0是经验参数, Sa= – (∂γ/∂T)p, 是表面熵。通过计算得到[C6py][DCA]的标准熵Sa= 61.6 × 10–3mJ·K–1·m–2。
另外,在不同温度下的表面能Ea可通过纯离子液体的表面张力值计算得到,计算公式如下:

将[C6py][DCA]的表面能Ea值列于表2。为了讨论表面能随温度的变化趋势,将Ea对T作图(见图3),拟合得到一条几乎平行于X轴的直线。这表明Ea与温度无关,而表面熵Sa是影响与温度有关的表面性质的主要因素。
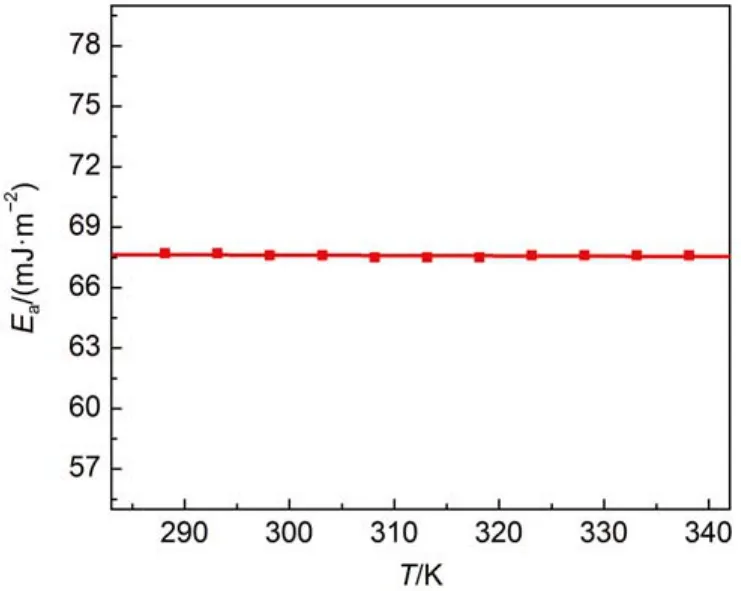
图3 288.15-338.15 K, [C6py][DCA]的Ea对T作图Fig.3 Plot of Eavs T of ILs [C6py][DCA] at the temperature range from 288.15 to 338.15 K
从表2的数据可以看出,离子液体的表面能比熔融盐要小,与有机液体更为接近(如熔融NaNO3的Ea= 146 mJ·m–2,苯的Ea= 72.1 mJ·m–2,正辛烷的Ea= 51.1 mJ·m–2)30,32。这说明,与无机熔融盐相比,离子液体的离子间相互作用相对较低,因为Ea只取决于离子之间的相互作用能。

图4 288.15-338.15 K, [C6py][DCA]的Rm和1024αp分别对T作图Fig.4 Plots of Rmand the polarization coefficient (1024αp) vs T of ILs [C6py][DCA] at the temperature range from 288.15 to 338.15 K
3.4 [C6py][DCA]的摩尔极化度和极化率

由Rm和αp间的Lorentz-Lorenz关系,可得到Rm的定义式33:根据上式,可以计算出在288.15–338.15 K温度范围内,离子液体[C6py][DCA]的Rm和αp,并将结果列于表2中。分别将得到的Rm和αp值对T做图(见图4),拟合后可以看出,Rm和αp的值与温度无关,Rm和αp反映了离子液体的诱导偶极作用。
3.5 用Eötvös方程预测离子液体[C6py][DCA]的表面张力
对于大多数的离子液体,其表面张力值随着温度的升高而减小,其关系可用下列Eötvös方程32,34表示:


图5 288.15-338.15 K, [C6py][DCA]的γV2/3对T作图Fig.5 Plot of γV2/3vs T of [C6py][DCA] at the temperature range from 288.15 to 338.15 K
Eötvös经验方程可以很好地解释表面张力和温度的关系,但是其中γV2/3的物理意义不明确且其单位J·mol–2/3也不方便使用。故本文提出了摩尔表面Gibbs自由能概念并对Eötvös经验方程进行了改进。
摩尔表面Gibbs自由能gs 可定义为

将公式(6)代入公式(5),摩尔表面Gibbs自由能和温度的关系可用下列经验方程表示:
式中Ci是经验参数,C1= – kEN1/3,C0= kEN1/3Tc,Tc=–C0/C1。由方程(6)计算得到的离子液体[C6py][DCA]的gs(exp)值对T作图,得到一条很好的直线(见图6),直线的拟合系数均大于0.99,标准偏差值在实验误差范围内。参数Ci值,标准偏差s,相关系数r及通过计算得到的离子液体的临界温度Tc值均列于表3,gs(exp)值列于表4。

图6 288.15-338.15 K, [C6py][DCA]的gs对T作图Fig.6 Plot of gsvs T of [C6py][DCA] at the temperature range from 288.15 to 338.15 K

表3 从方程(7)得到的C0, C1, r, s和Tc参数值Table 3 Parameter values of C0, C1, r, s, and Tcby empirical Eq.(7)
当温度升至临界温度Tc时,摩尔表面Gibbs自由能减至0,这样就从方程(7)变形得到了新的Eötvös方程:

上式为改进的Eötvös方程,参数C1和kE的关系与传统方程一样,C1= N1/3kE,单位是J·mol–1·K–1。尽管方程(5)和方程(8)都是经验方程,但后者中的每一项均有明显的物理意义和能量单位,这样更便于应用。在这个改进中,可以注意到方程将摩尔表面Gibbs自由能与液体的体积、密度和表面张力联系在一起,因此它可以发展为一种用来预测物质的物理性质的方法。
将方程(8)中的C1和Tc代入后,可以用来估算指定温度下离子液体的摩尔表面Gibbs自由能gs(est),gs(est)的估算值列于表4。再根据方程(6),就可以用得到的gs(est)值来估算离子液体的表面张力,γ(est)的估算值列于表4。将表面张力估算值γ(est)对其实验值γ(exp)作图,就可得到一条较好的直线(见图7)。拟合直线的斜率接近于1,拟合相关系数r = 0.999。上述事实说明表4中的γ(est)与表1中的γ(exp)能够较好的吻合。
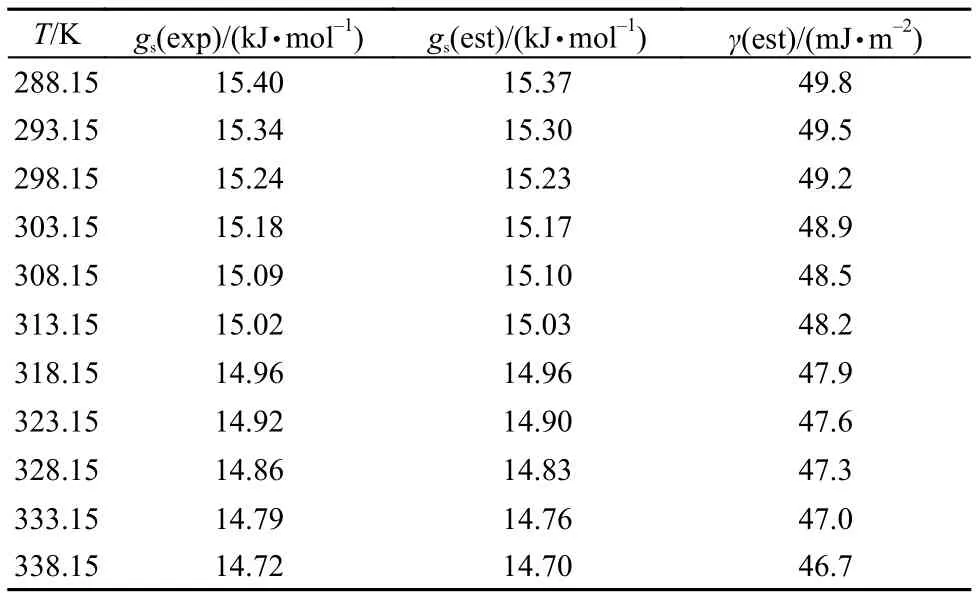
表4 288.15-338.15 K, [C6py][DCA]的gs(exp)、gs(est)及γ(est)值Table 4 gs(exp), gs(est), and γ(est) for [C6py][DCA] at the temperature range from 288.15 to 338.15 K

图7 表面张力的实验值γ(exp)对估算值γ(est)作图Fig.7 Plot of experimental γ(exp) values vs estimated γ(est) values
4 结 论
计算得到了离子液体[C6py][DCA]的Vm、Ea、Rm、αp,其中,Vm随着温度的升高略微增大,Ea、Rm和αp并不随温度的变化发生改变;本文还提出了摩尔表面积Gibbs自由能gs的概念,并对Eötvös方程进行改进,改进后的Eötvös方程的每一项物理量具有明确的物理意义,并可以与液体体积、密度、表面张力等联系一起,可以用来预测物质的物理化学性质。用新型Eötvös方程预测的离子液体[C6py][DCA]的表面张力值与实验值具有较好的一致性。
Supporting lnformation: available free of charge via the internet at http://www.whxb.pku.edu.cn.
(1)Seddon, K. R. J. Chem. Tech. Biotechnol. 1997, 68 (4), 351.
(2)Tao, G. H.; He, L.; Liu, W. S.; Xu, L.; Xiong, W.; Wang, T.;Kou, Y. Green Chem. 2006, 8, 639. doi: 10.1039/b600813e
(3)Muhammad, N.; Omar, W. N.; Man, Z.; Bustam, M. A.; Rafiq, S.; Uemura, Y. Ind. Eng. Chem. Res. 2012, 51 (5), 2280. doi: 10.1021/ie2014313
(4)Rout, A.; Binnemans, K. Ind. Eng. Chem. Res. 2014, 53 (8), 6500.
(5)Zhong, H. X.; Zhao, C. B.; Luo, H.; Zhang, L. Z. Acta Phys. -Chim. Sin. 2012, 28 (11), 2641. [仲皓想, 赵春宝, 骆 浩,张灵志. 物理化学学报, 2012, 28 (11), 2641.] doi: 10.3866/PKU.WHXB201207181
(6)Wang, H.; Xu, X. Q.; Shi, J. F.; Xu, G. Acta Phys. -Chim. Sin. 2013, 29 (3), 525. [王 海, 徐雪青, 史继富, 徐 刚. 物理化学学报, 2013, 29 (3), 525.] doi: 10.3866/PKU.WHXB201301091
(7)Zhao, D. B.; Fei, Z. F.; Geldbach, T. J.; Scopelliti, R.; Dyson, P. J. J. Am. Chem. Soc. 2004, 126 (48), 15876. doi: 10.1021/ja0463482
(8)Yunus, N. M.; Abdul Mutalib, M. I.; Man, Z.; Bustam, M. A.;Murugesan, T. Chemical Engineering Journal 2012, 189, 94.
(9)Calvar, N.; Gomez, E.; Macedo, E. A.; Dominguez, A. Thermochimica Acta 2013, 565, 178. doi: 10.1016/j.tca.2013.05.007
(10)Crosthwaite, J. M.; Muldoon, M. J.; Dixon, J. K.; Anderson, J. L.; Brennecke, J. F. Journal of Chemical Thermodynamics 2005,37 (6), 559. doi: 10.1016/j.jct.2005.03.013
(11)Xu, F.; Gao, H. S.; Dong, H. F.; Wang, Z. L.; Zhang, X. P.; Ren, B. Z.; Zhang, S. J. Fluid Phase Equilibria 2014, 365, 80. doi: 10.1016/j.fluid.2013.12.020
(12)Ye, Q.; Gao, T. T.; Wan, F.; Yu, B.; Pei, X. M.; Zhou, F.; Xue, Q. J. Journal of Materials Chemistry 2012, 22 (26), 13123. doi: 10.1039/c2jm31527k
(13)Zeng, S. J.; Gao, H. S.; Zhang, X. C.; Dong, H. F.; Zhang, X. P.;Zhang, S. J. Chemical Engineering Journal 2014, 251, 248. doi: 10.1016/j.cej.2014.04.040
(14)Jie, X. M.; Chau, J.; Obuskovic, G.; Obuskovic, G.; Sirkar, K. K. Industrial & Engineering Chemistry Research 2014, 53 (8), 3305. doi: 10.1021/ie403596b
(15)Schneider, S.; Hawkins, T.; Rosander, M.; Vaghjiani, G.;Chambreau, S.; Drake, G. Energy & Fuels 2008, 22 (4), 2871. doi: 10.1021/ef800286b
(16)Bedrov, D.; Borodin, O. Journal of Physical Chemistry B 2010,114 (40), 12802. doi: 10.1021/jp1049827
(17)Tokuda, H.; Hayamizu, K.; Ishii, K.; Susan, M. A. B. H.;Watanabe, M. Journal of Physical Chemistry B 2004, 108 (42), 16593. doi: 10.1021/jp047480r
(18)Krossing, I.; Slattery, J. M.; Daguenet, C.; Dyson, P. J.;Oleinikova, A.; Weingärtner, H. J. Am. Chem. Soc. 2006, 128(41), 13427.
(19)Jenkins, H. D. B.; Glasser, L. Inorganic Chemistry 2002, 41 (17), 4378. doi: 10.1021/ic020222t
(20)Jenkins, H. D. B.; Glasser, L. Inorganic Chemistry 2003, 42 (26), 8702. doi: 10.1021/ic030219p
(21)Ma, X. X.; Wei, J.; Zhang, Q. B.; Tian, F.; Feng, Y. Y.; Guan, W. Ind. Eng. Chem. Res. 2013, 52, 9490. doi: 10.1021/ie401130d
(22)Wei, J.; Chang, C.; Zhang, Y. Y.; Hou, S. Y.; Fang, D. W.; Guan, W. J. Chem. Thermodynamics 2015, 90, 310.
(23)Wei, J.; Zhang, Q. B.; Tian, F.; Zheng, L.; Guan, W.; Yang, J. Z. Fluid Phase Equilibria 2014, 371, 1. doi: 10.1016/j.fluid.2014.03.011
(24)Guan, W.; Zhang, Q. B.; Ma, X. X.; Wei, J.; Pan, Y.; Yang, J. Z. Fluid Phase Equilibria 2013, 360, 63. doi: 10.1016/j.fluid.2013.09.032
(25)Ma, X. X.; Wei, J.; Guan, W.; Pan, Y.; Zheng, L.; Wu, Y.; Yang, J. Z. J. Chem. Thermodynamics 2015, 89, 51. doi: 10.1016/j.jct.2015.02.025
(26)Guan, W.; Wang, C. X.; Wang, Z.; Chen, S. P.; Gao, S. L. Acta Chim. Sin. 2011, 69 (11), 1280. [关 伟, 王彩霞, 王 珍, 陈三平, 高胜利. 化学学报, 2011, 69 (11), 1280.]
(27)Earle, M. J.; Gordon, C. M.; Plechkova, N. V.; Seddon, K. R.;Welton, T. Analytical Chemistry 2007, 79 (2), 758. doi: 10.1021/ac061481t
(28)Gordon, C. M.; Muldoon, M. J.; Wagner, M. Ionic Liquids in Synthesis; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, 2002.
(29)Zhang, S. G.; Qi, X. J.; Ma, X. Y.; Lu, L. J.; Deng, Y. Q. J. Phys. Chem. B 2010, 114 (11), 3912. doi: 10.1021/jp911430t
(30)Lide, D. R. Handbook of Chemistry and Physics, 82nd ed.; CRC Press: Boca Raton, FL, 2001.
(31)Glasser, L. Thermochimica Acta 2004, 421 (1–2), 87. doi: 10.1016/j.tca.2004.03.015
(32)Adamson, A. W. Physical Chemistry of Surfaces, 3rd ed.; John Wiley: New York, 1976; translated by Gu, T. R. Science Press: Beijing, 1986. [Adamson, A. W. 表面物理化学. 第三版. 顾惕人译. 北京: 科学出版社, 1986.]
(33)Ersfeld, B.; Felderhof, B. U. Phys. Rev. E 1998, 57 (1), 1118. doi: 10.1103/PhysRevE.57.1118
(34)Tong, J.; Liu, Q. S.; Zhang, P.; Yang, J. Z. J. Chem. Eng. Data 2007, 52 (4), 1497. doi: 10.1021/je700102g
Thermodynamic Properties and Predicting the Surface Tension of Pyridinium-Based lonic Liquids of [C6py][DCA] Using a New Eötvös Equation
BU Xiao-Xue1FAN Ben-Han1WEI Jie1XING Nan-Nan1,2MA Xiao-Xue1GUAN Wei1,*
(1College of Chemistry, Liaoning University, Shenyang 110036, P. R. China;2College of Chemistry and Chemical Engineering, Huangshang University, Huangshan 245041, Anhui Province, P. R. China)
The pyridinium-based ionic liquids [C6py][DCA] (N-hexyl-pyridinium dicyanamide) was prepared and characterized using1H and13C nuclear magnetic responancec (NMR) spectroscopies, Fourier transform infrared (FT-IR) spectroscopy, and differential scanning calorimetry (DSC). The density (ρ), surface tension(γ), and refractiνe indices (nD) were measured at the temperature range from 288.15 to 338.15 K. Molecular νolume (Vm), energy of surface (Ea), molar polarization (Rm), and polarization coefficient of [C6py][DCA] (αp)were calculated from the experimental data. Ea, Rm, and αpwere approximately temperature-independent. The concept of molar surface Gibbs free energy (gs) was conceiνed, for which a new Eötνös equation was deriνed. The gs, critical temperature (Tc), and Eötνös empirical parameter related to polarity (kE) were also obtained. The new Eötνös equation was used to predict the surface tension and the predicted νalues of [C6py][DCA] are in close agreement with the corresponding experimental ones.
Pyridinium-based ionic liquid; Density; Surface tension; Molar surface Gibbs free energy; Eötνös equation
O643
10.3866/PKU.WHXB201510303
Received: September 9, 2015; Revised: October 28, 2015; Published on Web: October 30, 2015.
*Corresponding author. Email: guanweiy@sina.com.
The project was supported by the National Natural Science Foundation of China (21173107) and Liaoning Excellent Talents in University, China(2015025).
国家自然科学基金(21173107)和辽宁省高等学校优秀人才支持计划(2015025)资助项目
©Editorial office of Acta Physico-Chimica Sinica
