基于Butler方程Al-Mg-Er三元合金表面张力的计算

孙顺平，易丹青，臧 冰

(中南大学 材料科学与工程学院，长沙 410083)

基于Butler方程Al-Mg-Er三元合金表面张力的计算

孙顺平，易丹青，臧 冰

(中南大学 材料科学与工程学院，长沙 410083)

基于Butler方程，结合热动力学数据和CALPHAD优化的过剩吉布斯自由能参数，计算Al-Mg、Mg-Er和Al-Er二元合金的表面张力。结果表明：在镁熔体中加入元素铝和铒时，将增加该熔体的表面张力。通过计算Al-Mg、Mg-Er和Al-Er二元合金的过剩表面张力，发现过剩表面张力与过剩吉布斯自由能之间相对理想溶液偏差性质相反。选择铒为非对称性组元，并在此基础上结合Toop模型计算Al-Mg-Er三元合金的表面张力。结果表明：Al-Mg-Er三元合金的表面张力值基本在0.356～0.783 N/m之间，且随着铒含量的增加，表面张力呈增大的趋势。

Al-Mg-Er三元合金；表面张力；Butler方程；Toop模型

Abstract:Based on Butler’s equation, the surface tensions of Al-Mg, Mg-Er and Al-Er binary alloys were calculated in combination with thermodynamic data and excess Gibbs energies parameters calculated by CALPHAD technology. The results show that the surface tension of Mg melts increases with the additions of Al and Er. Calculating the excess surface tensions of Al-Mg, Mg-Er and Al-Er binary alloys, the excess surface tensions and excess Gibbs energies have an opposite deviation compared with ideal solution. Choosing Er as the asymmetric component in asymmetric model and combining with Toop model, the surface tension of Al-Mg-Er ternary alloy were calculated. The results indicate that the surface tension of Al-Mg-Er ternary alloy is approximately in the range of 0.356−0.783 N/m, and the surface tension increases with increasing the addition of Er element.

Key words:Al-Mg-Er ternary alloy; surface tension; Butler’s equation; Toop model

液态金属和合金的表面张力是金属熔体的重要物理参数之一，在材料、冶金、表面科学和界面与胶体科学等学科中有着重要作用。目前，表面张力的测量方法主要有最大泡压法、静滴法、电磁悬浮液滴法等[1]。由于测定合金熔体表面张力的实验过程难度大、花费高、耗时长，而且对于多元体系而言，组元较多，其数据十分庞大，因此利用各种理论和经验模型对合金熔体表面张力进行计算和预测就很有必要。

Butler方程将金属熔体的表面张力与表面相和体相的热力学性质联系起来，是目前国内外广泛运用的表面张力计算模型[1]。

国内外的研究人员运用该模型对多种体系熔体的表面张力进行了研究。TANAKA等[2]计算了Bi-Sn二元合金的表面张力，并且提出了计算合金表面张力的程序设计思想。QIAO等[3]运用人工神经网络方法预测纯元素表面张力，并结合热力学数据和CALPHAD技术，计算了包括熔盐物质在内的多元物质的表面张力。YAN等[4]在这一思想指导下，结合几何模型和通用溶液模型计算了Ni3S2-FeS-Cu2S三元熔体物质和Sn-Ga-In三元合金的表面张力，其计算值与实验值基本一致。LI等[5]运用静滴法开展了大量的实验研究，研究了Sb对熔融Si表面张力的影响，并测定了Sn-Bi二元合金的表面张力，其结果与Butler方程的计算结果有较好的符合。

稀土元素铒在铝合金中作用与钪相似，可有效提高合金的力学性能，改善其耐蚀性，且价格相对低廉，已成为一种重要的微合金元素[6]。目前，已有学者针对铒在Al-Mg合金中的存在形式与作用机理进行了一系列研究[7−8]。结果表明：铒与铝形成A13Er相，与基体共格或半共格析出，可以有效细化晶粒、提高合金的时效强化效果、改善合金热稳定性。WU等[9]研究了铒对挤压态Al-Mg合金组织和性能的影响，认为热加工后的固溶处理是改善该合金力学性能的关键性步骤。

由于有关稀土元素表面张力的研究还不多，相关的表面张力值和数据还很有限，而关于铒在铝合金中的表面张力的报道还很缺乏，因此，从理论上开展Al-Mg-Er三元合金的表面张力的研究具有重要的意义。本文作者运用Butler方程和Toop模型，计算Al-Mg-Er三元合金两两组元的表面张力，并在此基础上对Al-Mg-Er三元合金表面张力进行计算和分析，从而为进一步研究Al-Mg-Er三元合金的凝固过程和界面行为提供数据基础。

1 表面张力计算模型

1.1 Butler方程

BUTLER[10]提出将溶液表面看成表面相，假设表面相内组分与体相内组分在热力学上达到平衡，在此基础上推导出表面张力与热力学的关系，其表达式如下：

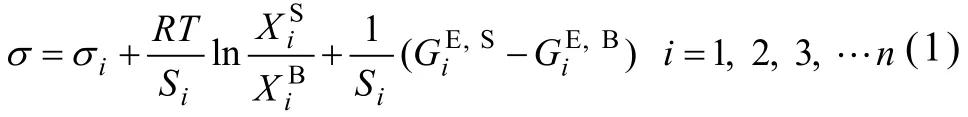
式中：σ和σi为溶液和纯组分i的表面张力，R为普适气体常数，T为绝对温度，和分别为组分i在表面相和体相中的摩尔分数，Si为组分i纯物质的单层表面积，其表达式如下：

式中：N0为阿伏伽德罗常数，ρi为纯组分i的密度，Mi为纯组分i的原子量。(GE,Si和GE,Bi分别为表面相和体相中组分i的偏摩尔吉布斯自由能，其中 G可以通过组分i的偏摩尔过剩自由能求的，组分i的偏摩尔过剩自由能和二元系的摩尔过剩自由能 GE的关系为

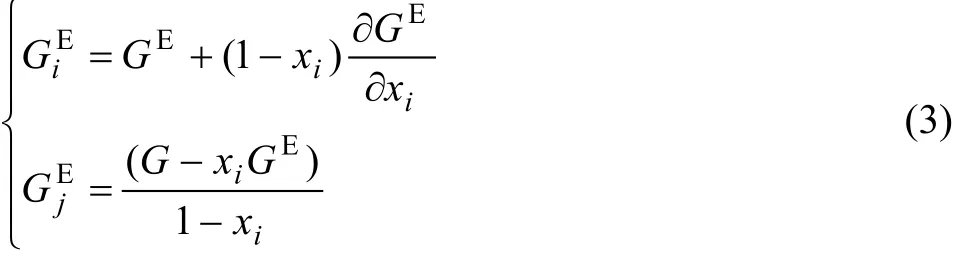
TANAKA等[2]认为表面相中组分i的偏摩尔吉布斯自由能与表面相中组分i的偏摩尔吉布斯自由能有相同的表达式，即

式中：β为半经验参数，主要取决于表面相和体相的配位数的比值ZS/ZB，假设熔体金属为密堆积结构，则体相原子配位数为12，而表相原子最近邻原子数为6，次近邻原子数为3，表相原子配位数为9，因此

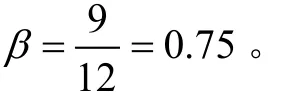
1.2 三元合金表面张力

三元系的性质可以通过几何模型由二元系的性质获得。目前常用的几何模型可分为两大类：对称模型(Kohler模型、Muggianu模型) 和非对称模型(Toop模型、Hillert模型)，还有近年来发展的通用溶液模型−Chou模型[11]。非对称模型由于考虑了组元之间的性质差异，因而相比对称模型有着更好的精度，而通用溶液模型−Chou模型克服了非对称组元选择上的困难，不过其计算过程包含大量的积分运算，相对繁琐，因而在外推三元系的热力学性质的计算中，仍较多采用Toop模型。

利用Toop模型计算三元系的过剩表面张力，首先要选取非对称组元，即以两个相互作用程度相近的二元系的公共组元作为三元系的非对称组元。在A-B-C三元系中，当组元B和C为对称组元，组元A为非对称组元时，可通过以下方程由3个二元系的过剩表面张力外推出三元系A-B-C的过剩表面张力[12]。σE=xBσE(x,1-x)+

ABC x+x ABA A

BC xCσE(x,1-x)+

x+x ACA A

BC

(x+ x)2σE(xB,xC) (5)

BCBCx+x x+x

BC BC

式中：xi(i=A, B, C)为组元i在三元系中的摩尔分数，和分别为A-B-C三元系和i−j二元系的过剩表面张力。其中可由i−j二元系的表面张力σ 与i和jij纯组分的表面张力求得，其表达式如下：

三元系的表面张力与三元系的过剩表面张力及其理想熔体的表面张力存在如下关系：

2 计算结果与讨论

二元系的过剩热力学函数用R-K多项式，其公式表示如下：

式中：xi为组元i的摩尔分数，为二元素过剩热力学函数，An和Bn为待定参数，可由热力学和相图的计算机耦合(CALPHAD)求得。Al-Mg、Mg-Er和Al-Er过剩热力学函数如表1所列。铝、镁和铒各元素的相关物理化学参数如表2所列。

表1 Al-Mg、Mg-Er和Al-Er过剩热力学函数Table 1 Excess Gibbs energies of Al-Mg, Mg-Er and Al-Er binary alloys at 1 773 K

2.1 Al-Mg、Mg-Er和Al-Er表面张力计算

图1所示为Al-Mg、Mg-Er和Al-Er二元合金在1 773 K的表面张力计算曲线，反映了3种合金表面张力随其组元成分的变化规律。从图1可以看出，在镁熔体中加入铝和铒都将增加合金的表面张力。值得注意的是，随着铝元素的摩尔分数增加，Al-Er二元合金表面张力呈现先增加后下降的趋势，出现明显的反常现象。

表2 纯金属的表面张力、密度和原子量数据Table 2 Data of surface tension, density and atomic mass of pure metal

从图1(b)所示的表面相与体相的成分关系可以看出，Al-Mg二元合金中的铝元素在该二元系表面相中含量较少，即镁元素在该二元系表面富集。另外，从图1(d)所示的表面相与体相的成分关系可以看出，Mg-Er二元合金中的镁元素在该二元系表面富集，我们认为这主要是由于纯镁表面张力值相比于铒和铝较小，易于表面偏聚。XIAO等[16]运用改进静滴法测量了Ni-(Cr, Co, W)合金中的表面张力，提出表面张力小的元素容易在表面偏聚。我们的计算结果与该观点相吻合。

2.2 Al-Mg、Mg-Er和Al-Er过剩表面张力

为了便于确定Al-Mg-Er三元合金的非对称组元，我们将Al-Mg、Mg-Er和Al-Er的过剩吉布斯自由能绘图，如图2所示。从图2可以看出，Mg-Er和Al-Er的过剩吉布斯自由能相似，且都不同于Al-Mg，因而Al-Mg-Er三元系是非对称的。在这非对称的三元系中，热力学性质对称的两个二元系的公共组元Er应该被选为热力学非对称组元。这一点可以从3种元素在元素周期表中的位置得到解释，铝元素和镁元素都是第三周期主族元素且原子序数相近，而铒元素是第六周期、ⅢB族元素，属重稀土元素，其性质与铝元素和镁元素有着较大差异。

由Al-Mg、Mg-Er和Al-Er二元合金的表面张力可以计算Al-Mg-Er三元合金的过剩表面张力，如图3所示。

比较图2和3可以看出，过剩表面张力与过剩吉布斯自由能之间存在一定的规律性，即GE和σE相对理想溶液偏差性质相反。当体系的过剩吉布斯自由能对理想溶液呈正偏差时，相应体系的表面张力对理想溶液呈负偏差；而当体系的过剩吉布斯自由能对理想溶液呈负偏差时，相应体系的表面张力对理想溶液呈正偏差。

这一点可以从Butler方程的表达式中找到解释。一般而言，Butler方程右式第二相的影响小于右式第三项，合金的表面张力主要由Butler方程右式第三项决定。当体系的过剩吉布斯自由能对理想溶液呈正偏差时，即过剩吉布斯自由能GE为正值时，依据式(4)，为负值，Butler方程的计算结果表现为合金的表面张力值比纯组元表面张力值要小，即相应体系的表面张力对理想溶液呈负偏差。反之，当体系的过剩吉布斯自由能对理想溶液呈负偏差时，即GE为负值时，为正值，合金的表面张力值比纯组元表面张力值要大，即相应体系的表面张力对理想溶液呈正偏差。

图1 Al-Mg、Mg-Er和Al-Er二元合金在1 773 K的计算表面张力曲线及表面相与体相的成分关系Fig.1 Calculated surface tensions of Al-Mg, Mg-Er and Al-Er binary alloys and relationship between compositions in surface and in bulk phases at 1 773 K: (a), (b) Al-Mg; (c), (d) Mg-Er; (e), (f) Al-Er

上述观点有利于我们解释Al-Er二元合金表面张力的反常现象。一方面，由于铝、铒元素之间亲和力较强，相互作用复杂，铝、铒元素之间过剩吉布斯自由能对理想溶液呈负偏差，且偏差数值较大，必然表现为Al-Er二元合金表面张力对理想溶液呈正偏差，其偏差数值也较大，这一原因导致Al-Er二元合金表面张力的增幅随着铝元素的摩尔分数增加而呈先增大后减少的趋势；另一方面，根据混合法则，Al-Er二元合金表面张力随着铝元素的摩尔分数增加有增大的趋势。这两种影响的共同作用导致了Al-Er二元合金表面张力的反常，即该二元合金表面张力的增幅总体上呈先增大后减小的趋势，并在x(Al)约为0.65处达到极大值。该结论仍需进一步深入的理论及实验研究来证实。

图2 Al-Mg, Mg-Er和Al-Er在1 773 K的过剩吉布斯自由能Fig.2 Excess Gibbs energies of Al-Mg, Mg-Er and Al-Er binary boundary alloys at 1 773 K(x=x(Al), x(Mg))

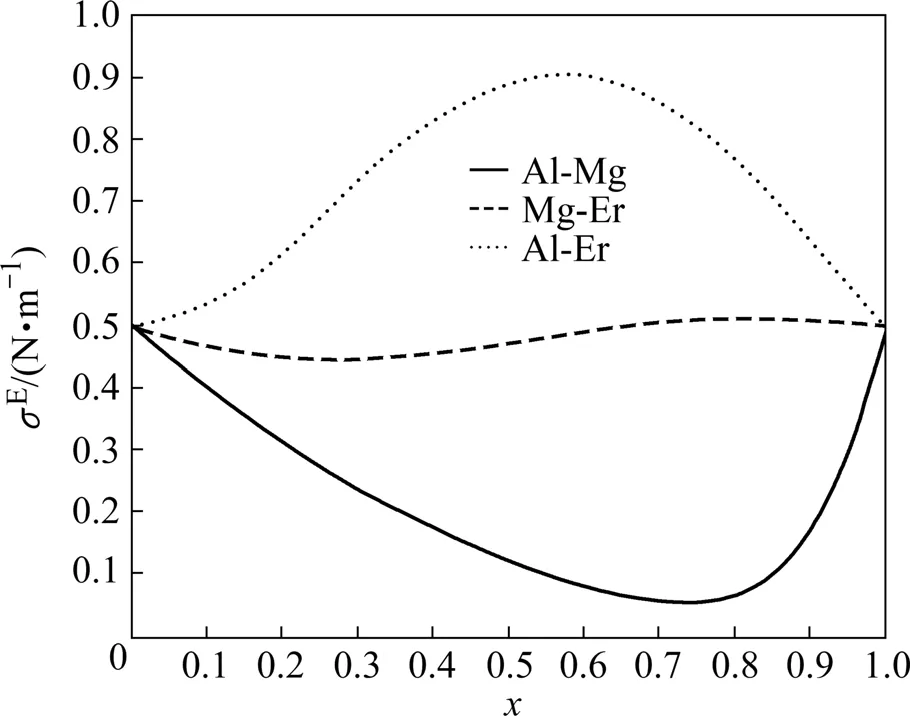
图3 Al-Mg、Mg-Er和Al-Er在1 773 K的过剩表面张力Fig.3 Excess surface tensions of Al-Mg, Mg-Er and Al-Er binary boundary alloys at 1 773 K(x=x(Al), x(Mg))

2.3 Al-Mg-Er三元合金表面张力计算

为了更好地研究某一组元在三元系中的作用，可以将除此组元之外的另外两组元固定成一比例，研究该组元成分变化对该三元系表面张力的影响，即研究该三元系过一元素点的垂直截面。我们选择研究的各垂直截面的成分比例如表3所列。

表3 Al-Mg-Er系研究的各垂直截面Table 3 Cross sections in Al-Mg-Er system investigated

Al-Mg-Er三元合金表面张力与各元素的摩尔分数之间的关系如图4所示。从图4中可以看出，在Al-Mg-Er三元合金表面张力随各元素的摩尔分数的变化主要呈现单调增加或者减小的趋势，这一点与二元合金表面张力变化规律相一致。图4(a)中的D和E曲线呈现一定的抛物线特征，这主要是由于镁元素的摩尔分数较少，其曲线与Al-Er二元合金的表面张力曲线接近。

从图4中可以发现，过铒元素点的垂直截面表面张力曲线(见图4(a))和过铝元素点的垂直截面表面张力曲线(见图4(b))变化趋势接近，而过镁元素点的垂直截面的表面张力曲线(见图4(c))与前两者明显不同，这主要是由于其曲线受到Al-Er二元合金的表面张力的影响。Al-Er二元合金表面张力的增幅随着铝元素的摩尔分数的增加呈现先增加后下降的趋势，所以过镁元素点的垂直截面表面张力曲线随着铒铝摩尔分数比x(Er)/x(Al)增加也表现为先增大后减小。

将图4中各表面张力曲线外延可得到该曲线与纵坐标的交点，这些交点分别对应着Al-Mg-Er三元系特殊成分点的表面张力值。当该元素的摩尔分数趋于零时，Al-Mg-Er三元系转变为不含该组元的二元系，其表面张力值由三元系中另外两组元的表面张力及其相对摩尔分数决定；当摩尔分数为1时，Al-Mg-Er三元系转变为仅含该组元的一元系，其表面张力值即为该纯组元的表面张力。

为了更好地研究Al-Mg-Er三元合金表面张力，让结果显示更加清晰，我们计算了该三元系表面张力的等值线，将其投影到三元相图的等温截面上，结果如图5所示。

从图5中可以看出，Al-Mg-Er三元合金成分三角形对应的表面张力值基本处于0.356～0.783 N/m之间，且随着铒含量的增加，表面张力呈增大的趋势。三元合金表面张力的最大值为0.783 N/m，对应的成分点位于Al-Er二元合金边界上，x(Al)约为0.65；而表面张力的最小值为0.356 N/m[1]，且对应的成分点位于富镁角。

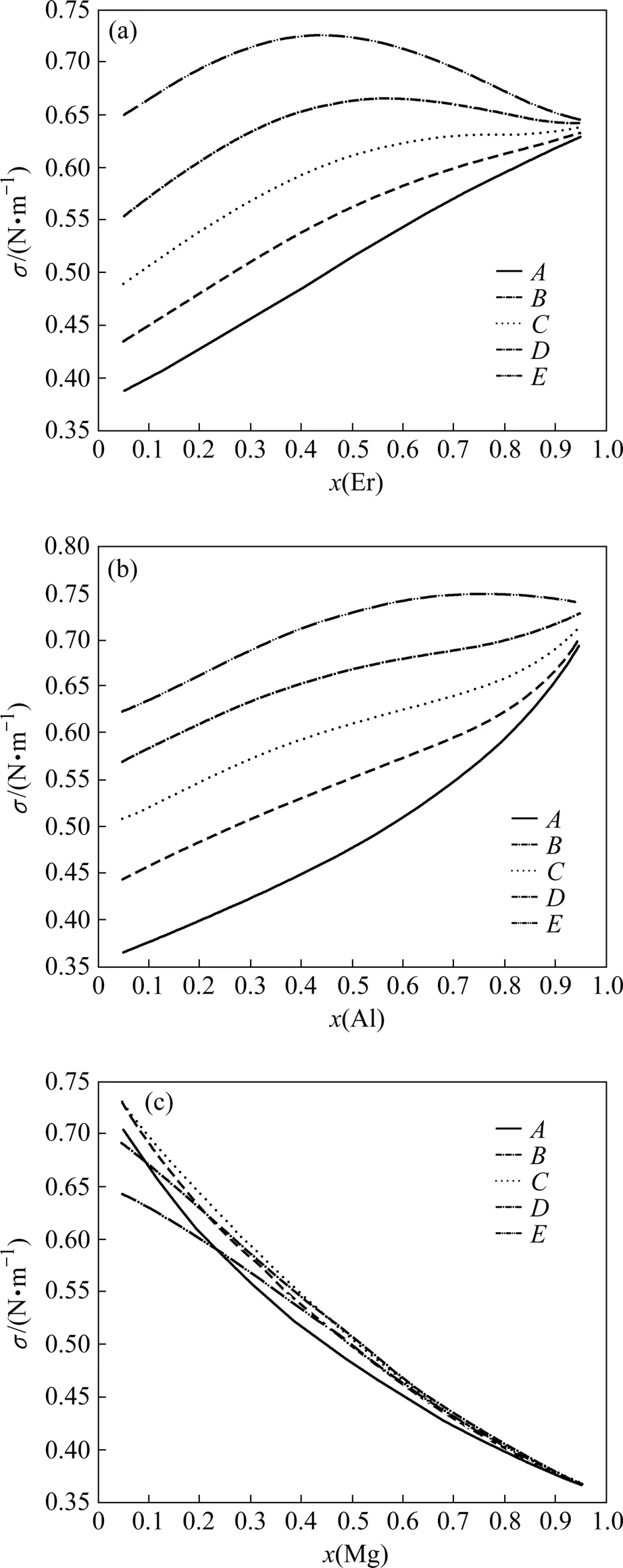
图4 Al-Mg-Er三元合金在1 773 K的表面张力Fig.4 Surface tensions of Al-Mg-Er ternary alloy at 1 773 K:(a) From Er corner; (b) From Al corner; (c) From Mg corner

图5 Al-Mg-Er三元合金在1 773 K的表面张力等值线投影图Fig.5 Plots of iso-lines of surface tensions in Al-Mg-Er ternary alloy at 1 773 K

3 结论

1) 在镁熔体中加入铝和铒，都将增加该熔体的表面张力，而Al-Er二元合金表面张力出现明显的反常现象。

2) 过剩表面张力与过剩吉布斯自由能之间存在一定的规律性，即GE和σE相对理想溶液偏差性质相反。

3) Al-Mg-Er三元合金成分三角形的表面张力值基本处于0.356～0.783 N/m之间，随着铒含量的增加，表面张力呈增大的趋势。

REFERENCES

[1] 袁章福, 柯家骏, 李 晶. 金属及合金的表面张力[M]. 北京:科学出版社, 2006.YUAN Zhang-fu, KE Jia-jun, LI Jing. Surface tension of metal and alloy[M]. Beijing: Science Press, 2006.

[2] TANAKA T, HACK K, HARA S.Calculation of surface tension of liquid Bi-Sn alloy using thermochemical application library Chem App[J]. Calphad, 2000, 24(4): 465−474.

[3] QIAO Zhi-yu, YAN Li-jun, CAO Zhan-min. Surface tension prediction of high-temperature melts[J]. Journal of Alloys and Compounds, 2001, 325(1): 180−189.

[4] YAN Li-jun, ZHENG Shao-bo, DING Guo-ji. Surface tension calculation of the Sn–Ga–In ternary alloy[J]. Calphad, 2007,31(1): 112−119.

[5] LI Jing, YUAN Zhang-fu, QIAO Zhi-yu. Measurement and calculation of surface tension of molten Sn–Bi alloy[J]. Journal of Colloid and Interface Science, 2006, 297(1): 261−265.

[6] ROSALBINO F, ANGELINI E, de NEGRI S, SACCONE A,DELFINO S. Influence of the rare earth content on the electrochemical behaviour of Al–Mg–Er alloys[J]. Intermetallics,2003, 11(5): 435−441.

[7] 徐国富, 杨军军, 金头男. 微量稀土Er对Al-5Mg合金组织与性能的影响[J]. 中国有色金属学报, 2006, 16(5): 768−774.XU Guo-fu,YANG Jun-jun, JIN Tou-nan. Effects of trace rare-earth element Er on microstructure and properties of Al-5Mg alloy[J]. The Chinese Journal of Nonferrous Metals,2006, 16(5): 768−774.

[8] 邢泽炳, 聂祚仁, 季小兰. 微量Er, Mn对Al-Mg合金组织与性能的影响[J].稀有金属材料与工程, 2006, 35(12): 1979−1982.XING Ze-bing, NIE Zuo-ren, JI Xiao-lan. Effect of trace element erbium and manganese on microstructure and properties of Al-Mg alloy[J]. Rare Metal Materials and Engineering, 2006,35(12): 1979−1982.

[9] WU Z G, SONG M, HE Y H. Effects of Er on the microstructure and mechanical properties of an as-extruded Al–Mg alloy[J].Mater Sci Eng A, 2009, 504(1): 183−187.

[10] BUTLER J A V. The thermodynamics of the surfaces of solutions[J]. Proceedings of the Royal Society of London A,1932, 135: 348−375.

[11] MANASIJEVIĆ D, ŽIVKOVIĆ D, ŽIVKOVIĆ Ž. Prediction of the thermodynamic properties for the Ga–Sb–Pb ternary system[J]. Calphad, 2003, 27(4): 361−366.

[12] TOOP G W. Predicting ternary activities using binary data[J].Transactions of the American Institute of Mining, 1965, 233(5):850−855.

[13] ZUO Y, CHANG Y A. Thermodynamic calculation of the Al-Mg phase diagram[J]. Calphad, 1993, 17(2): 161−174.

[14] CACCIAMANI G, SACCONE A, NEGRI S D. The Al-Mg-Er ternary system partⅡ: Thermodynamic modeling[J]. Journal of Phase Equilibria, 2002, 23(1): 38−50.

[15] ZHANG L G, LIU L B, HUANG G X, QI H Y, JIA B R, JIN Z P.Thermodynamic assessment of the Al–Cu–Er system[J]. Calphad,2008,32(3): 527−534.

[16] XIAO Feng, LIU Lan-xiao, YANG Ren-hui. Surface tension of molten Ni-(Cr, Co, W) alloys and segregation of elements[J].Trans Nonferrous Met Soc China, 2008, 18(5): 1184−1188.

(编辑 何学锋)

Calculation of surface tension of Al-Mg-Er ternary alloy based on Butler’s equation

SUN Shun-ping, YI Dan-qing, ZANG Bing(School of Materials Science and Engineering, Central South University, Changsha 410083, China)

TG146. 1

A

1004-0609(2010)05-0930-07

2009-07-15；

2009-12-16

易丹青，教授，博士；电话：0731-88830263；E-mail: yioffice@mail.csu.edu.cn