基于新一代密度泛函和神经网络势能面的量子反应动力学计算

2016-11-18苏乃强陈俊徐昕张东辉

物理化学学报 2016年1期

苏乃强陈俊徐昕张东辉

（1复旦大学化学系，分子催化与功能材料上海市重点实验室，物质计算科学教育部重点实验室，上海 200433；2中国科学院大连化学物理研究所，分子反应动力学国家重点实验室，理论与计算化学研究中心，辽宁大连 116023）

苏乃强1,§陈俊2,§徐昕1,*张东辉2,*

介绍了近年来发展起来的新一代密度泛函XYG3及利用神经网络构造分子体系势能面的最新进展。以H3和CH5等体系为实例，表明基于高效准确的密度泛函电子结构计算，与神经网络高精度势能面构造的理想结合，可以得到可靠的化学动力学结果，并有望用于更大更复杂的体系。

密度泛函；势能面；神经网络；第一性原理；反应动力学

1 引言

随着激光、分子束、微弱信号检测等技术的成功发展与应用，化学动力学实验研究的重点和前沿，已推进到“态-态反应动力学”的新阶段1–3。分子束技术可以选定反应物的平动能和测定产物的速度分布。激光可以用于选定反应物的内能态以及探测反应产物的内能态分布。根据这些详细的信息，人们已有办法深入到微观领域，在原子分子层面以及量子态的水平上研究化学反应过程。

与此同时，近几十年来量子化学理论方法和计算技术的发展，也大大促进了化学动力学的理论研究4–6。在Born-Oppenheimer近似下，首先进行电子和核运动的分开处理。然后通过求解电子运动的Schrödinger方程，获得不同核构型下的势能值。据此，人们可以构造出反应势能面（PES），并进一步地给出原子核运动的理论描述。所得到的分子振转光谱、化学反应速率常数、反应共振、态-态反应微分截面等信息，可以直接和相应的实验结果进行比对，揭示化学反应过程的微观机理。

特别是，近年来理论与实验的紧密结合，取得了丰硕的成果7–15。所研究的体系，涉及到激光化学、大气化学、燃烧化学等一系列极其重要的化学基元反应，极大地促进了人们对化学反应本质的理解。

从理论的角度，可靠的动力学结果的获得取决于势能面的准确性，而势能面的准确性又依次取决于计算势能值的电子结构方法的准确性，以及将一系列离散的势能计算值生成解析形式的势能函数的准确性。对于电子结构计算，现在普遍采用高等级的后自洽场方法，如多参考组态相互作用（MRCI）方法，或者耦合簇（CC）等方法，而且计算必须结合大的基函数。例如，最近的F + H2体系的计算16，就用到CCSD（T）及aug-cc-pV6Z。这样的电子结构计算极其昂贵，每步计算需要耗费极大的计算资源和时间，因而往往无法对反应所涉及的各种可能核构型进行充分取样，尤其是对包含较多原子的反应体系，随自由度的增加，举步维艰。另一方面，解析势能函数的获得，目前主要通过插值法和拟合法。较为常用的插值法有样条插值方法，和Collins等17–20发展的改进的Shepard插值方法等等。前者虽然可以达到很高的精度9,21，但需要大量的电子结构计算点，不适合于超过4原子的体系。后者则有一系列的多原子体系的势能面的成功构造例子，如四原子的OH3体系13,22，六原子的CH5体系23等。插值方法的一个严重缺点是，在随后的动力学计算过程中势能函数的计算量特别大，而函数拟合方法克服了这一缺点，因而从三原子到超过六原子的体系中都有应用24–29。很多种函数形式都被用于拟合势能面，这包括LEPS（London-Eyring-Polanyi-Sato）势函数30，多项式展开方法31–33以及Bowman等发展的交换不变多项式（PIP）方法34–39等等。但普通的函数拟合方法在高维体系中一个常见的缺点是拟合精度不足，这成为了动力学方法应用的一个亟待克服的瓶颈。

本文首先介绍密度泛函理论近年来的一个重要发展，XYG3型双杂化泛函40–45可以以类似于MP2的计算速度，获得和CCSD（T）相比拟的精度。然后介绍近年来在使用神经网络构造分子体系势能面的重要进展46。两者的结合，可以得到高精度的势能面，给出可靠的化学动力学结果47，并有望推广到更大更复杂的体系。

2 新一代的密度泛函方法XYG3

量子力学理论告诉我们，求解定态Schrödinger方程可以得到包括体系电子能量在内的大量信息。然而除了极少数的几个体系，关于这个方程的严格求解非常困难。尽管如此，我们仍然有一个个如何得到越来越精确解的方案——从头算后自洽场方法48，这种方法包括：多元体系微扰方法（MP2，MP3，···），组态相互作用方法（CID, CISD,···），耦合簇方法（CCD，CCSD，···）等。然而这样的方法对于越来越高的精度要求，计算量的增长却越来越快，这常常使我们望而却步。权衡精度和计算量，密度泛函理论（DFT）方法，特别是Kohn-Sham （KS）方法，往往是科学家们研究中进行各种能量和性质计算一种最佳的选择。

2.1 传统Kohn-Sham方法

传统的KS方法49首先定义了一个无相互作用体系，即KS体系，该体系的Hamiltonian Hs写为

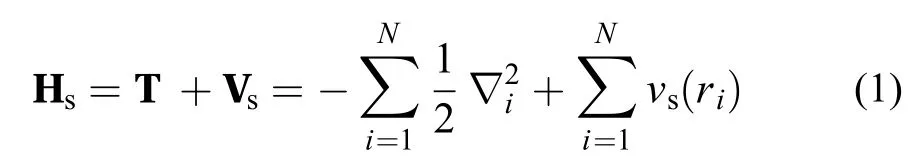
其中T为电子动能算符，而Vs为一选定的定域外势。由于不存在电子–电子相互作用，KS体系的Schrödinger方程容易求解，体系的波函数在无简并的情况下可表示为单Slater行列式，即这里的单电子函数 ψi 被称为KS轨道，可由KS本征方程得到。

其中前N个KS轨道为占据轨道，可以用来得到体系的基态密度

也用来构成KS态Ф，进而精确地求解出无相互作用体系的动能Ts［n］

这样体系的基态电子总能量可以写成如下的泛函形式：

并由此定义了交换相关能

其中T［n］为体系的动能，Vext［n］为电子与外势相互作用能（一般为电子–原子核库仑相互作用能），Vee［n］为电子–电子库仑相互作用能，U［n］为电子–电子间经典库仑相互作用能。因此，由（6）式所定义的交换相关能Exc［n］中不仅包含了电子–电子相互作用能中的量子效应，而且也包含了体系真实动能与KS体系动能的差异。

注意到，定域外势Vs的选取是为了保持KS体系的基态密度与真实体系的基态密度相等。这是通过比对两体系的化学势而实现的。由此给出

迄今，KS框架下精确的交换相关泛函仍然未知，但已经有大量的近似形式被提出，并被成功地运用于不同的化学问题研究中41–43。当Exc［n］取为电子密度n的纯泛函形式，而不显含KS轨道或轨道能时，如局域密度近似（LDA）50,51、广义梯度近似（GGA）52–54等，即为传统的KS方法。这类泛函精度有限，需要进一步推广。

2.2 绝热途径与杂化方法

绝热途径55,56是杂化泛函方法的理论基础。这里定义的绝热途径为，找一条平滑的路径连接KS体系和真实体系的基态，且在这条路径上的所有体系均保持基态密度不变。常用的途径为

λ称为耦合常数，用于开关电子–电子相互作用。体系Hλ的基态波函数用Ψλ表示，通过选择外势Vλ以保持体系的基态密度维持不变。当λ = 0，体系为电子–电子相互作用完全关闭的KS体系，Ψλ= Ф和Vλ= Vs；当λ = 1，体系为真实体系，Ψλ= Ψ和Vλ= Vext。

通过耦合常数积分，绝热途径给出了交换相关能的如下定义

其中

从式（9）可知，交换相关泛函可以通过被积函数Wλ的合理近似来得到，这就为设计近似泛函提供了另一个可行的方法。

基于绝热途径，Becke引入了杂化泛函57。首先利用简单的线性模型来近似函数Wλ，即

并通过绝热途径的起止点来最终确定模型

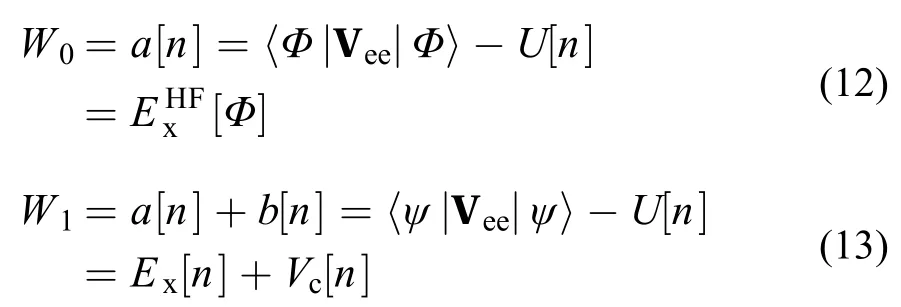
结合式（9）、（11）和（14）便可得到Becke的half and half杂化泛函57

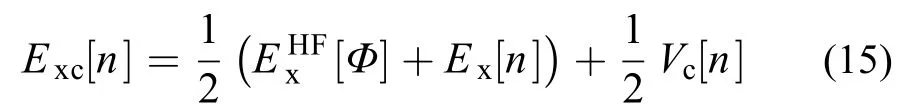
Becke这一工作强调了刻画好绝热途径起始点的重要性，为交换泛函中引入HF型交换能提供了一个理论依据。这促使了大量优秀的杂化泛函的诞生。其中以B3LYP58,59为代表

这里B88表示Becke88交换泛函52，LYP表示Lee-Yang-Parr相关泛函53；（16）式中的三个参数是通过和相应的实验值优化得到的，为｛c1, c2, c3｝ = ｛0.20, 0.72, 0.81｝。

杂化泛函的出现是近似密度泛函发展的一大飞越。相对于GGA近似泛函，其表现有了全面的改善。特别地，B3LYP泛函的整体表现出色，是目前运用最为广泛的泛函之一。

2.3 XYG3型双杂化泛函

XYG3型泛函的发展，继承和发展了Becke的杂化泛函发展的思路。同样从式（11）的线性模型出发，来近似函数。不同的是，模型是通过起点与起点的梯度来确定的60

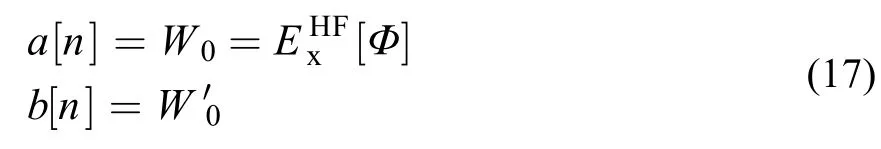
利用Görling-Levy二阶微扰理论（GL2）61,62，可以得到

这里以i、j表示占据轨道指标，a、b表示空轨道指标；υx和f分别表示定域交换势算符和HF形式离域交换势算符。除包括形式上和MP2相关能类似的双电子贡献外，还包含单电子的贡献。但由于后者比前者贡献小得多，因而可以暂且不显式地考虑。由此可得泛函60,63

与式（15）相对应。和前面half and half杂化泛函启发我们HF型交换能可以作为交换泛函的一个成分一样，式（20）进一步告诉我们可作为相关泛函的一个成分，进而可引入双杂化泛函。因而双杂化泛函是指在杂化泛函的基础上，进一步在相关泛函部分引入型的相关能。

首个依照绝热途径理论建立的双杂化泛函为XYG360，其形式为

相当于式（20）与式（15）或（16）的某种线性组合。XYG3包含三个混合参数，它们是通过以G3/9964–66中的生成热（HOF）数据为训练集优化得到的，优化结果为｛a1,a2,a3｝=｛0.8033, 0.2107, 0.3211｝。由于双杂化泛函无法直接进行自洽计算得到轨道，必须要有对应的母泛函为其提供KS轨道和基态密度来计算泛函中的各部分能量。有文献研究表明，B3LYP泛函所得到的密度与高等级从头算得到的密度较为接近67，因而将B3LYP作为XYG3的母泛函是一个合理的选择。XYG3泛函对于体系各种性质的计算表现都相当优秀，下一节将会给出关于这个泛函的一些测试结果。

随后，其他XYG3型的双杂化泛函被陆续提出，比如，XYGJ-OS63和xDH-PBE068。这两个泛函只显式地计算MP2相关能中自旋反平行（OS）的贡献，而自旋平行（SS）的贡献分别交由VWN或PBE相关泛函处理。这样可以将原来MP2的N5标度降低到N3–N4（这里N表示体系的大小）。XYGJ-OS和xDH-PBE0是目前文献中计算速度最快的双杂化泛函。PBE-ACDH是一个无拟合参数的双杂化泛函69，它是目前文献中唯一的基于PBE轨道，不忽略GL2中的单电子贡献，严格考虑电子密度缩放的双杂化泛函。另外，XYG3型的双杂化泛函的解析梯度理论和程序化也得到了实现，可以进行平衡态、过渡态的自动搜索70。

2.4 XYG3型双杂化泛函表现

双杂化泛函的表现已有很多的系统评测40–45,68–85。所评测的性质包括生成热、键解离能、电离能、电子亲和能、反应能垒和非键相互作用等诸多方面。本文着重讨论各类泛函在过渡态能垒和过渡态结构上的表现。

Truhlar及合作者构建了HTBH38/0486和NHTBH38/0487两个测试集，分别对应于在给定过渡态构型下的38个氢转移（HT）及38个非氢转移反应沿正、逆方向的能垒，而后者又可进一步分为12个重原子转移（HAT）、16个亲核取代（NS）和10个单分子（UN）反应等三种反应类型。图1示出各种计算方法在反应能垒计算上的平均绝对偏差（MAD）。对于总的76个反应能垒计算，LDA（SVWN550,51）的MAD高达62.4 kJ·mol–1，而GGA的MAD分别为36.4 kJ·mol–1（PBE54）和34.3 kJ·mol–1（BLYP52,53）。B3LYP已经是个很大的进步，较GGA的误差减半，MAD降为18.0 kJ·mol–1。而XYG3的精度已趋于化学精度，MAD为4.2 kJ·mol–1，可以和基于组态相互作用的QCISD（T）方法精度相媲美。图1也示出低等级从头算HF和MP2的表现，它们显然远比XYG3逊色。特别值得注意的是，很多方法对不同的反应类型，误差差别很大。因而这类方法很容易对反应机理给出有失偏颇的描述。

图1 各种方法对Truhlar的HTBH38/04和HTBH38/04反应能垒集测试集86，87计算的平均绝对偏差（MAD）42，44Fig.1 Mean absolute deviations （MAD） computed on the Truhlar′s HTBH38/04 and HTBH38/04 testing sets86，87using different methods42，44

Truhlar及其同事88,89还构建了一个TSG48集，对以上四种反应类型各收集了3个，共12个过渡态的结构，着重考察各类方法对成键和断键的距离的描述好坏。由于QCISD（T）没有解析梯度，因而用QCISD代替，进行高等级的构型优化。

如图2所示，很显然，LDA（SVWN5）及GGA（BLYP，PBE）方法优化的过渡态构型极不可靠，平均键长误差往往大于10 pm。事实上，这类方法有时甚至不能给出定性正确的过渡态结构。杂化泛函如B3LYP较GGA和LDA有很大的进步，平均误差可以控制在7 pm左右。XYG3较B3LYP又有很大的进步，总MAD为1.60 pm，可以与QCISD的结果（MAD = 1.55 pm）相媲美。

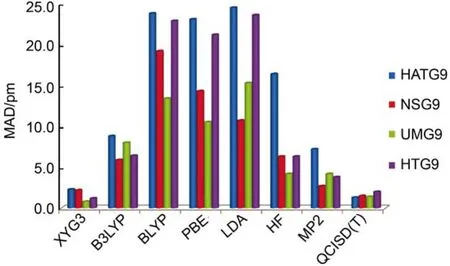
图2 各种方法对Truhlar过渡态构型集88，89的MAD42，44Fig.2 MAD computed on the Truhlar’s TSG48 testing set88，89using different methods42，44

3 基于神经网络的分子体系势能面构造

神经网络（NN）作为一种数学工具，已经在化学领域被广泛应用90–93。它不仅可以用来处理海量的化学数据，进行结构与反应的识别和分类，建立光谱等性质与物质结构的关系，还可以用于预测分子性质和新型反应。利用神经网络构造势能面也已经有不少研究94–121。它作为一种通用型的拟合方法，理论上可以拟合出任意的函数形式122，因而有望用来克服一般函数拟合方法在高维体系中拟合精度不足的缺陷。然而，如何系统地选择新构型进行电子结构计算、直至构造出动力学结果可靠收敛的势能面，仍然是一个困难的工作。

3.1 前向网络

图3 神经网络函数结构示意图Fig.3 Illustration of neural network functions46

前向网络122是神经网络中一种较为简单的类型，常用于化学反应势能面构造。图3（a）示意出一个具有两个隐含层的前向网络结构，每一个节点称为一个神经元。图3（b）示意出其中一个神经元的运算规则分别被称为第m层的第i个神经元的输入值和输出值被称为激发函数。输入层和输出层的激发函数一般用线性函数，而对于隐藏层，激发函数一般取为非线性函数，比如双曲正切函数tanh。参数是连接第m – 1层第i个神经元与第m层第j个神经元的权重是第m层第j个神经元的偏置。对于如图3所示的神经网络，可用矩阵表示为

在分子反应势能面的拟合中，输入层往往对应于分子构型的坐标x，一般用分子的内坐标或者原子距离来表示，输出层对应势能值E。

3.2 神经网络的拟合方法

在拟合过程中，过度拟合是一个常见的问题。预防过度拟合的一个常用方法是所谓的“早期停止”法124。这种方法在拟合之前将所有数据按一定的比例分为用于真正的拟合的“训练集”，和另一部分用于测试的“测试集”。拟合过程中，如果训练集和测试集的误差都一直下降，则认为没有发生过度拟合。当训练集的误差在下降，但测试集的RMSE开始连续上升若干步时，就表明发生了过度拟合，此时停止拟合，并把前面测试集RMSE最小的那一步作为拟合结果。

3.3 分子构型的选择方法

构型的选择是势能面构造的关键。完备的构型集合需要覆盖在一定能量范围内所有可能的反应通道，并且在过渡态、反应中间体等重要构型的位置附近包括更多的数据。本文介绍新近发展和完善的一套系统选择构型的方案46，通过多次添加构型以及拟合，最终的势能面能够得到收敛的反应动力学结果。

（1）最初构型的收集和NN-PES的初步构造：最初的一批数据点一般通过低精度的从头算动力学方法，比如基于半经验或者HF/STO-3G水平下的BOMD方法，计算少量轨线得到。当然也可以利用以往文献中势能面构造的已知构型。在这些构型的基础上，基于每两个构型之间的欧氏距离进行筛选，剔除掉在空间上离得很近的构型点，从而得到第一批构型的集合。然后对这些构型进行电子结构计算，使用NN方法进行拟合，得到了最初版本的势能面。

（2）构型的多次添加和NN-PES的逐步完善：在初级势能面上，选择不同的碰撞能和初始振转态，进行大量的准经典轨线计算。进一步筛选轨线所经历的构型，寻找新的构型，用于新一轮的从头算和势能面拟合。应注意，在过渡态、反应中间体等重要构型的位置附近，需包括更多的数据；在NN-PES拟合误差较大的区域，应添加更多的数据；以及对几次拟合得到的NN-PES相差较大的区域，应添加更多的数据。本步骤重复几次之后，几次拟合得到的NN-PES的标准差和最大偏差应该足够小，准经典轨线计算不再预示新构型的添加。

（3）最终势能面的构造和反应动力学结果的产出：这时开始测试量子动力学的结果。可靠的势能面必须满足两个要求，一是拟合误差足够小，使用多次拟合的势能面计算得到同样的动力学结果；二是从头算构型的数目足够多，覆盖范围足够广，再继续增加（或略减少一些）从头算构型用于拟合而不会改变动力学结果。

4 XYG3型密度泛函和神经网络势能面的结合

近年来，大量从三原子到六原子的基于高等级从头算的高精度NN-PES14–16,125–129被成功构建。但昂贵的高等级的从头算，限制了其在更高维体系的应用。以下我们将以H3和CH5两个体系为实例，介绍基于高效准确的XYG3型密度泛函电子结构计算与神经网络高精度势能面构造的结合的结果。这为量子动力学向更大更复杂的体系的应用打下好的契机。

4.1 三原子体系H3

人们也一直期待密度泛函的发展最终能提供足够的精度，能准确地描述H3体系135，这是利用密度泛函理论描述更复杂体系的基础。图4是各种电子结构计算方法给出的H + H2→ H2+ H反应的最小能量路径（MEP）。从图可知LDA（SVWN5）完全不能描述该反应，在本该的能垒位置出现了极小点。GGA泛函（BLYP和PBE）表现也不佳，不仅能垒太低，而且MEP在能垒附近的形状不合理，出现很宽的平台，且略带浅阱。B3LYP给出定性上开始趋于合理的MEP，但太低的能垒高度（比BKMP2低0.233 eV）也将会显著影响其对动力学的描述。从图4还可以看出，低等级的从头算（HF和MP2）高估能垒的倾向明显。而M06-2X方法的能垒高度，已经和MP4相近，虽然其MEP形状偏宽。在计算过程中还发现，M06-2X的自洽场收敛非常困难。另一方面，XYG3的结果和BKMP2参考值趋于定量吻合，XYG3的能垒仅比BKMP2的低0.041 eV。这标志着密度泛函精度的一个显著提升。

图4 各种计算方法给出的H + H2→ H2+ H反应的最小能量路径47Fig.4 Minimal energy path of H + H2→ H2+ H reaction computed by different methods47

图5比较了由XYG3和BKMP2势能面计算的H + H2→ H2+ H反应几率随平动能的变化。其中反应物H2处于振转基态，总角动量为0，碰撞能量设在2.0 eV以下。总体而言，XYG3的结果和BKMP2的符合很好，可以忠实地反映出反应几率随平动能变化的各个细节。B3LYP则极大地低估了反应阈值，严重高估低能区的反应几率，反应几率随动能变化过于激烈，完全不能用于该体系的动力学描述。

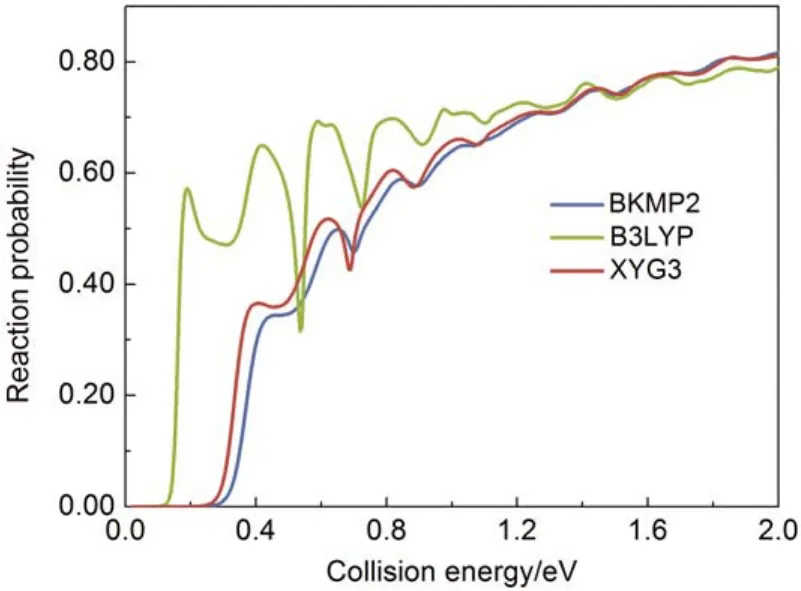
图5 在B3LYP、XYG3和BKMP2势能面上计算的H + H2= 0， j = 0） → H2+ H反应几率随平动能的变化47Fig.5 Probabilities of H + H2= 0， j = 0） → H2+ H reaction as a function of collision energy from B3LYP，XYG3， and BKMP2 potential energy surfaces （PES）47

由于该H + H2→ H2+ H反应主要是在排斥的、倾向于共线（即3个H原子排列在一条直线）的基态势能面上进行的，所以产物分子H2会逆着H原子进来的方向“反弹”回去，产物的分布主要是后向散射，但由于体系在经历过渡态区域时可能发生“时间延迟”1,2，从而可能产生一些前向散射的产物。

图6画出由B3LYP、XYG3和BKMP2势能面计算的在碰撞能分别为0.8、1.0和1.5 eV时的微分截面。图中不同层的同心圆代表产物不同的振转态，层的高度代表产物分布的强度。XYG3给出了和BKMP2很吻合的微分截面，合理的产物分布。相比较，B3LYP给出的微分截面则十分不同，不仅夸大了前向散射的产物分布强度，而且错误地低估了后向散射的产物分布强度。这意味着B3LYP给出的反应机理不是普遍接受的“直接型”（direct type），而是涉及某种中间复合物的机理6。

图6 由不同势能面计算的H + H2→ H2+ H反应在碰撞能分别为0.8、1.0和1.5 eV时的微分截面47Fig.6 Differential cross sections of H + H2→ H2+ H reaction at collision energies of 0.8， 1.0， and 1.5 eV from different PESs47

4.2 六原子体系CH5

H + CH4→ H2+ CH3是甲烷燃烧过程中的一个重要基元反应，因此无论理论上还是实验上对这个反应都有很多的研究136–141。第一个基于从头算能量的势能面构建于2004年5，但此势能面只是描述了过渡态附近的信息，不能用于更为详细的全域动力学计算。第一套全域势能面（ZBB1，ZBB2和ZBB336,142）出现在2006年，基于超过20000个RCCSD（T）/aug-cc-pVTZ水平的高精度从头算数据。2010年，全域的ZFWCZ势能面23,143被构造出来，它基于29999个构型在UCCSD（T）水平下使用aug-cc-pVTZ基组的能量以及6-311++G（3df,2pd）基组的一阶导数和二阶导数。目前最精确的势能面是2014年使用神经网络拟合方法构造的XCZ（Xu-Chen-Zhang）-NN势能面128，从头算是在UCCSD（T）-F12a/aug-cc-pVTZ水平下进行的。整个势能面的构造从ZFWCZ和ZBB3已经使用的50000多个构型开始。首先使用构型之间的欧氏距离筛选，大约保留8000个构型用于第一批从头算。为了提高拟合效率以及构型选择的效率，将整个势能面按相应键长分为（i） H + CH4渐近区，（ii） H2+ CH3渐近区，以及（iii） CH5相互作用区。按照第3.3节的流程对这三个区域分别循环地增加新构型，并最后进行量子动力学结果测试。最终在全部的空间内一共选择了47783个构型，得到了收敛的动力学结果。2015年，在这些构型基础上又增加了15258个处于H2+ CH3渐近区和高能量区域的构型，即一共使用63041个构型，使用交换不变多项式与神经网络相结合的PIP-NN方法144构造出了包含相同H原子交换对称性的势能面129。基于PIP-NN势能面的动力学结果与XCZ-NN高度吻合，但程序的运算速度有很大的提高。

与PIP-NN势能面的拟合方式一样，我们基于63041个XYG3/aug-cc-pVTZ的电子结构数据构造了新的PES。以UCCSD（T）-F12a/aug-cc-pVTZ结果为参考值，我们比较了XYG3及一些密度泛函和低等级从头算的表现。其结果简介如下。

图7是各种电子结构计算方法给出的H + CH4→H2+ CH3反应的MEP。从图可知从头算的HF和MP2方法严重高估反应能垒，必须到MP4以上，才能给出较好的结果。密度泛函M06-2X方法，已经能给出和MP4相近的能垒高度，但对于H + CH4渐近区描述差强人意。在计算过程中也发现，这一区域M06-2X的自洽场非常难收敛。其他一些常用泛函，如B3LYP和PBE等，严重低估反应能垒，而LDA（SVWN5）则完全不能描述该反应。从图7可以看出，XYG3的结果和CCSD（T）参考值在整个MEP高度吻合。

图7 各种方法计算的H + CH4→ H2+ CH3反应的最小能量路径Fig.7 Minimal energy path of H + CH4→ H2+ CH3reaction computed by different methods

图8比较了使用7维量子波包方法145在XYG3和CCSD（T）势能面上计算的H + CH4→ H2+ CH3反应几率随平动能的变化。其中反应物CH4处于振转基态，总角动量分别为0、20及40，碰撞能量设在1.6eV以下。总体而言，XYG3的结果和CCSD（T）的符合较好，特别是在三个角动量的反应阈值和低能部分，符合程度很高，而在高能部分也能反映出反应几率随平动能变化的各个细节，虽然XYG3的反应几率略有偏低。可以预言B3LYP将极大地高估反应几率，而MP2将极大地低估反应几率。

图8 由XYG3和CCSD（T）势能面计算的H + CH4（v = 0，j = 0） → H2+ CH3反应几率随平动能的变化Fig.8 Probabilities of H + CH4（v = 0， j = 0） → H2+ CH3reaction as a function of collision energy from XYG3 and CCSD（T） PESs

图9 由CCSD（T），XYG3，B3LYP和MP2势能面计算的H + CH4（v = 0， j = 0） → H2+ CH3反应速率常数随温度的变化Fig.9 Rate constants of H + CH4（v = 0， j = 0） → H2+ CH3reaction as a function of temperature from CCSD（T），XYG3， B3LYP， and MP2 PESs

图9比较了由XYG3和CCSD（T）势能面计算的H + CH4→ H2+ CH3反应速率常数随温度的变化。该反应速率常数是基于CH4处于振转基态时Jtot为0、20、40的7维量子反应几率（图8），用JShifting方法146计算的结果。总体而言，XYG3的结果和CCSD（T）的结果在整个温度区域内高度吻合，在500到1500 K的温度区间内两者仅相差3%左右。在低温处（300 K），XYG3的结果也仅比CCSD（T）低10%。而B3LYP给出的反应速率常数偏高一个数量级以上，相应地MP2给出的反应速率常数偏低一个数量级以上。另外，相比于XYG3和CCSD（T）的结果，B3LYP的反应速率常数随温度的变化更平缓，而MP2的变化更急剧，两者都在低温区域有高达三个数量级的误差。XYG3的优秀表现为量子动力学向更大更复杂的体系的应用打下好的契机。

5 结束语

近二十年多年来，化学动力学的研究逐渐深入到了原子分子以及量子态的层次，反应过渡态的研究从过渡态的几何结构研究进入到量子化过渡态的研究，而分子动态过程的研究由基态的动力学扩展到了激发态的动力学研究。化学反应动力学的研究也由单势能面的绝热动力学深入到了多势能面的非绝热动力学研究。而反应过程的时间尺度的研究也从微秒、纳秒走向飞秒、阿秒。另一方面，动力学研究也从基元反应的态-态动力学研究扩展到了大分子体系，多元体系以及界面和凝聚相体系等复杂体系的动力学研究。这一系列的研究构成了当代化学反应动力学研究的主要前沿课题。而复杂体系的动力学研究则已经成为化学动力学研究最为重要的前沿课题。这些都要求有更高效准确的电子结构计算方法和更可靠精确的势能面构造方法。

本文介绍了近年来发展起来的新一代密度泛函，XYG3型双杂化泛函，它可以以类似于MP2的计算速度，获得和CCSD（T）相比拟的精度。本文还介绍了新近发展和完善的一套系统选择构型的方案，通过多次添加构型以及拟合，最终的基于神经网络构造的势能面能够得到收敛的反应动力学结果。两者的结合，有望推广到更大更复杂的动力学体系，使化学反应动力学的研究上一个新台阶。

（1）Yang, X. M. Int. Rev. Phys. Chem. 2005， 24, 37. doi: 10.1080/01442350500163806

（2）Yang, X. M. Annu. Rev. Phys. Chem. 2007， 58, 433. doi: 10.1146/annurev.physchem.58.032806.104632

（3）Clary, D. C. Science 2008， 321, 789. doi: 10.1126/science.1157718

（4）Zhang, D. H.； Collins, M.； Lee, S. Science 2000， 290, 961. doi:10.1126/science.290.5493.961

（5）Wu, T.； Werner, H. J.； Manthe, U. Science 2004， 306, 2227. doi: 10.1126/science.1104085

（6）Guo, H. Int. Rev. Phys. Chem. 2012， 31, 1. doi: 10.1080/0144235X.2011.649999

（7）Harich, S. A.； Dai, D. X.； Wang, C. C.； Yang, X. M.； Chao, S. D.； Skodje, R. T. Nature 2002， 419, 281. doi: 10.1038/nature01068

（8）Dai, D. X.； Wang, C. C.； Harich, S. A.； Wang, X. Y.； Yang, X. M.； Chao, S. D.； Skodje, R. T. Science 2003， 300, 1730. doi: 10.1126/science.1084041

（9）Qiu, M. H.； Ren, Z. F.； Che, L.； Dai, D. X.； Harich, S. A.；Wang, X. Y.； Yang, X. M.； Xu, C. X.； Xie, D. Q.； Gustafsson, M.； Skodje, R. T.； Sun, Z. G.； Zhang, D. H. Science 2006， 311, 1440. doi: 10.1126/science.1123452

（10）Che, L.； Ren, Z. F.； Wang, X. G.； Dong, W. R.； Dai, D. X.；Wang, X. Y.； Zhang, D. H.； Yang, X. M.； Sheng, L. S.； Li, G. L.； Werner, H. J.； Lique, F.； Alexander, M. H. Science 2007，317, 1061. doi: 10.1126/science.1144984

（11）Wang, X. A.； Dong, W. R.； Xiao, C. L.； Che, L.； Ren, Z. F.；Dai, D. X.； Wang, X. Y.； Casavecchia, P.； Yang, X. M.； Jiang, B.； Xie, D. Q.； Sun, Z. G.； Lee, S. Y.； Zhang, D. H.； Werner, H. J.； Alexander, M. H. Science 2008， 322, 573. doi: 10.1126/science.1163195

（12）Dong, W. R.； Xiao, C. L.； Wang, T.； Dai, D. X.； Yang, X. M.；Zhang, D. H. Science 2010， 327, 1501. doi: 10.1126/science.1185694

（13）Xiao, C. L.； Xu, X.； Liu, S.； Wang, T.； Dong, W. R.； Yang, T. G.； Sun, Z. G.； Dai, D. X.； Xu, X.； Zhang, D. H.； Yang, X. M. Science 2011， 333, 440. doi: 10.1126/science.1205770

（14）Wang, T.； Chen, J.； Yang, T. G.； Xiao, C. L.； Sun, Z. G.；Huang, L.； Dai, D. X.； Yang, X. M.； Zhang, D. H. Science 2013， 342, 1499. doi: 10.1126/science.1246546

（15）Yang, T. G.； Chen, J.； Huang, L.； Wang, T.； Xiao, C. L.； Sun, Z. G.； Dai, D. X.； Yang, X. M.； Zhang, D. H. Science 2015， 347, 60. doi: 10.1126/science.1260527

（16）Chen, J.； Sun, Z. G.； Zhang, D. H. J. Chem. Phys. 2015， 142, 024303. doi: 10.1063/1.4904546

（17）Ischtwan, J.； Collins, M. J. Chem. Phys. 1994， 100, 8080. doi: 10.1063/1.466801

（18）Thompson, K. C.； Jordan, M.； Collins, M. J. Chem. Phys. 1998，108, 564. doi: 10.1063/1.475419

（19）Bettens, R.； Collins, M. J. Chem. Phys. 1999， 111, 816. doi: 10.1063/1.479368

（20）Collins, M.； Zhang, D. H. J. Chem. Phys. 1999， 111, 9924. doi: 10.1063/1.480344

（21）Xu, C. X.； Xie, D. Q.； Zhang, D. H. Chin. J. Chem. Phys. 2006，19, 96. doi: 10.1360/cjcp2006.19

（22）Yang, M. H.； Zhang, D. H.； Collins, M.； Lee, S. Y. J. Chem. Phys. 2001， 115, 174. doi: 10.1063/1.1372335

（23）Zhou, Y.； Fu, B. N.； Wang, C. R.； Collins, M.； Zhang, D. H. J. Chem. Phys. 2011， 134, 064323. doi: 10.1063/1.3552088

（24）Maisuradze, G.； Thompson, D. J. Phys. Chem. A 2003， 107, 7118. doi: 10.1021/jp030144a

（25）Maisuradze, G.； Thompson, D.； Wagner, A.； Minkoff, M. J. Chem. Phys. 2003， 119, 10002. doi: 10.1063/1.1617271

（26）Guo, Y.； Kawano, A.； Thompson, D.； Wagner, A.； Minkoff, M. J. Chem. Phys. 2004， 121, 5091. doi: 10.1063/1.1777572

（27）Maisuradze, G.； Kawano, A.； Thompson, D.； Wagner, A.；Minkoff, M. J. Chem. Phys. 2004， 121, 10329. doi: 10.1063/1.1810477

（28）Kawano, A.； Maisuradze, G. J. Biol. Phys. Chem. 2006， 6, 37.

（29）Dawes, R.； Passalacqua, A.； Wagner, A.； Sewell, T.； Minkoff, M.； Thompson, D. J. Chem. Phys. 2009， 130, 144107. doi: 10.1063/1.3111261

（30）Sato, S. J. Chem. Phys. 1955， 23, 592. doi: 10.1063/1.1742043

（31）Boothroyd, A.； Keogh, W.； Martin, P.； Peterson, M. J. Chem. Phys. 1996， 104, 7139. doi: 10.1063/1.471430

（32）Bian, W. S.； Werner, H. J. J. Chem. Phys. 2000， 112, 220. doi: 10.1063/1.480574

（33）Capecchi, G.； Werner, H. J. Phys. Chem. Chem. Phys. 2004， 6, 4975. doi: 10.1039/b411385c

（34）Ayouz, M.； Babikov, D. J. Chem. Phys. 2013， 138, 164311. doi: 10.1063/1.4799915

（35）Li, J.； Wang, Y. M.； Jiang, B.； Ma, J. Y.； Dawes, R.； Xie, D. Q.；Bowman, J.； Guo, H. J. Chem. Phys. 2012， 136, 041103. doi: 10.1063/1.3680256

（36）Xie, Z.； Bowman, J.； Zhang, X. B. J. Chem. Phys. 2006， 125, 133120. doi: 10.1063/1.2238871

（37）Czakó, G.； Bowman, J. Phys. Chem. Chem. Phys. 2011， 13, 8306. doi: 10.1039/C0CP02456B

（38）Czakó, G.； Bowman, J. J. Chem. Phys. 2012， 136, 044307. doi: 10.1063/1.3679014

（39）Yang, J. Y.； Shao, K. J.； Zhang, D.； Shuai, Q.； Fu, B. N.；Zhang, D. H.； Yang, X. M. J. Phys. Chem. Lett. 2014， 5, 3106. doi: 10.1021/jz5016923

（40）Zhang, I. Y.； Wu, J.； Xu, X. Chem. Commun. 2010， 46, 3057. doi: 10.1039/C000677G

（41）Zhang, I. Y.； Xu, X. A New-Generation Density Functional Towards Chemical Accuracy for Chemistry of Main Group Elements； Heidelberg: Springer, 2014.

（42）Zhang, I. Y.； Xu, X. Int. Rev. Phys. Chem. 2011， 30, 115. doi: 10.1080/0144235X.2010.542618

（43）Zhang, I. Y.； Xu, X. Prog. Chem. 2012， 24, 1023.

（44）Su, N. Q.； Xu, X. Sci. China Chem. 2013， 43, 1761. doi: 10.1360/032013-258

（45）Su, N. Q.； Xu, X. Int. J. Quantum Chem. 2015， 115, 589. doi: 10.1002/qua.24849

（46）Chen, J.； Zhang, D. H. Sci. Sin. Chim. 2015， 45, 1241. doi: 10.1360/N032015-00148

（47）Su, N. Q.； Chen, J.； Sun, Z. G.； Zhang, D. H.； Xu, X. J. Chem. Phys. 2015， 142, 084107. doi: 10.1063/1.4913196

（48）Shavitt, I.； Bartlett, R. J. Many-Body Methods in Chemistry and Physics. MBPT and Coupled-Cluster Theory； CambridgeUniversity Press: Now York, 2009.

（49）Kohn, W.； Sham, L. J. Phys. Rev. 1965， 140, A1133. doi: 10.1103/PhysRev.140.A1133

（50）Slater, J. C. Quamtum Theory of Molecules and Solids: v4； New York: McGraw-Hill Inc, 1974.

（51）Vosko, S. H.； Wilk, L.； Nusair, M. Can. J. Phys. 1980， 58, 1200. doi: 10.1139/p80-159

（52）Becke, A. D. Phys. Rev. A 1988， 38, 3098. doi: 10.1103/PhysRevA.38.3098

（53）Lee, C. T.； Yang, W. T.； Parr, R. G. Phys. Rev. B 1988， 37, 785. doi: 10.1103/PhysRevB.37.785

（54）Perdew, J. P.； Burke, K.； Ernzerhof, M. Phys. Rev. Lett. 1996，77, 3865. doi: 10.1103/PhysRevLett.77.3865

（55）Gunnarsson, O.； Lundqvist, B. I. Phys. Rev. B 1976， 13, 4274. doi: 10.1103/PhysRevB.13.4274

（56）Langreth, D. C.； Perdew, J. P. Phys. Rev. B 1977， 15, 2884. doi: 10.1103/PhysRevB.15.2884

（57）Becke, A. D. J. Chem. Phys. 1993， 98, 1372. doi: 10.1063/1.464304

（58）Becke, A. D. J. Chem. Phys. 1993， 98, 5648. doi: 10.1063/1.464913

（59）Stephens, P. J.； Devlin, F. J.； Chabalowski, C. F.； Frisch, M. J. J. Phys. Chem. 1994， 98, 11623. doi: 10.1021/j100096a001

（60）Zhang, I. Y.； Xu, X.； Goddard, W., III. Proc. Natl. Acad. Sci. U. S. A. 2009， 106, 4963. doi: 10.1073/pnas.0901093106

（61）Görling, A.； Levy, M. Phys. Rev. B 1993， 47, 13105. doi: 10.1103/PhysRevB.47.13105

（62）Görling, A.； Levy, M. Phys. Rev. A 1994， 50, 196. doi: 10.1103/PhysRevA.50.196

（63）Zhang, I. Y.； Xu, X.； Jung, Y. S.； Goddard, W. A., III. Proc. Natl. Acad. Sci. U. S. A. 2011， 108, 19896. doi: 10.1073/pnas.1115123108

（64）Curtiss, L. A.； Raghavachari, K.； Trucks, G. W.； Pople, J. A. J. Chem. Phys. 1991， 94, 7221. doi: 10.1063/1.460205

（65）Curtiss, L. A.； Raghavachari, K.； Redfern, P. C.； Pople, J. A. J. Chem. Phys. 1997， 106, 1063. doi: 10.1063/1.473182

（66）Curtiss, L. A.； Raghavachari, K.； Redfern, P. C.； Pople, J. A. J. Chem. Phys. 2000， 112, 7374. doi: 10.1063/1.481336

（67）Cremer, D. Mol. Phys. 2001， 99, 1899. doi: 10.1080/00268970110083564

（68）Zhang, I. Y.； Su, N. Q.； Brémond, É. A. G.； Adamo, C. J. Chem. Phys. 2012， 136, 174103. doi: 10.1063/1.3703893

（69）Su, N. Q.； Xu, X. J. Chem. Phys. 2014， 140, 18A512. doi: 10.1063/1.4866457

（70）Su, N. Q.； Zhang, I. Y.； Xu, X. J. Comput. Chem. 2013， 34, 1759. doi: 10.1002/jcc.23312

（71）Su, N. Q.； Adamo, C.； Xu, X. J. Chem. Phys. 2013， 139, 174106. doi: 10.1063/1.4827024

（72）Zhang, I. Y.； Xu, X. J. Phys. Chem. Lett. 2013， 4, 1669. doi: 10.1021/jz400695u

（73）Zhang, I. Y.； Luo, Y.； Xu, X. J. Chem. Phys. 2010， 133, 104105. doi: 10.1063/1.3488649

（74）Zhang, I. Y.； Luo, Y.； Xu, X. J. Chem. Phys. 2010， 132, 194105. doi: 10.1063/1.3424845

（75）Zhang, I. Y.； Wu, J. M.； Luo, Y.； Xu, X. J. Chem. Theory Comput. 2010， 6, 1462. doi: 10.1021/ct100010d

（76）Zhang, I. Y.； Wu, J. M.； Luo, Y.； Xu, X. J. Comput. Chem. 2011， 32, 1824. doi: 10.1002/jcc.21764

（77）Zhang, I. Y.； Xu, X. Phys. Chem. Chem. Phys. 2012， 14, 12554. doi: 10.1039/c2cp40904f

（78）Rao, L.； Zhang, I. Y.； Guo, W.； Xu, X. J. Comput. Chem. 2013，34, 1636. doi: 10.1002/jcc.23303

（79）Liu, G.； Wu, J.； Zhang, I. Y.； Chen, Z. N.； Xu, X. J. Phys. Chem. A 2011， 115, 13628. doi: 10.1021/jp207641g

（80）Zhou, Y. W.； Zhang, I. Y.； Wu, J. M.； Wu, A. A.； Xu, X. Chin. J. Chem. Phys. 2011， 24, 635. doi: 10.1088/1674-0068/24/06/635-639

（81）Shen, C.； Zhang, I. Y.； Fu, G.； Xu, X. Chin. J. Chem. Phys. 2011， 24, 249. doi: 10.1088/1674-0068/24/03/249-252

（82）Zhang, I. Y.； Xu, X. ChemPhysChem 2012， 13, 1486. doi: 10.1002/cphc.201100909

（83）Su, N. Q.； Zhang, I. Y.； Wu, J. M.； Xu, X. Front. Chem. China 2011， 6, 269. doi: 10.1007/s11458-011-0256-3

（84）Su, N. Q.； Yang, W. T.； Mori-Sanchez, P.； Xu, X. J. Phys. Chem. A 2014， 118, 9201. doi: 10.1021/jp5029992

（85）Su, N. Q.； Xu, X. J. Phys. Chem. A 2015， 119, 1590. doi: 10.1021/jp507711t

（86）Zhao, Y.； Lynch, B. J.； Truhlar, D. G. Phys. Chem. Chem. Phys. 2005， 7, 43. doi: 10.1039/B416937A

（87）Zhao, Y.； Gonzales-Garcia, N.； Truhlar, D. G. J. Phys. Chem. A 2005， 109, 2012. doi: 10.1021/jp045141s

（88）Zheng, J.； Zhao, Y.； Truhlar, D. G. J. Chem. Theory Comput. 2009， 5, 808. doi: 10.1021/ct800568m

（89）Xu, X.； Alecu, I. M.； Truhlar, D. G. J. Chem. Theory Comput. 2011， 7, 1667. doi: 10.1021/ct2001057

（90）Wu, J. M.； Xu, X. J. Chem. Phys. 2007， 127, 214105. doi: 10.1063/1.2800018

（91）Wu, J. M.； Xu, X. J. Chem. Phys. 2008， 129, 164103. doi: 10.1063/1.2998231

（92）Wu, J. M.； Xu, X. J. Comput. Chem. 2009， 30, 1424. doi: 10.1002/jcc.21164

（93）Wu, J. M.； Zhang, I. Y.； Xu, X. ChemPhysChem 2010， 11, 2561. doi: 10.1002/cphc.201000273

（94）Blank, T.； Brown, S.； Calhoun, A.； Doren, D. J. Chem. Phys. 1995， 103, 4129. doi: 10.1063/1.469597

（95）Brown, D.； Gibbs, M.； Clary, D. C. J. Chem. Phys. 1996， 105, 7597. doi: 10.1063/1.472596

（96）Gassner, H.； Probst, M.； Lauenstein, A.； Hermansson, K. J. Phys. Chem. A 1998， 102, 4596. doi: 10.1021/jp972209d

（97）Prudente, F.； Acioli, P.； Soares, N. J. Chem. Phys. 1998， 109, 8801. doi: 10.1063/1.477550

（98）Raff, L.； Malshe, M.； Hagan, M.； Doughan, D.； Rockley, M.；Komanduri, R. J. Chem. Phys. 2005， 122, 084104. doi: 10.1063/1.1850458

（99）Witkoskie, J.； Doren, D. J. Chem. Theory Comput. 2005， 1, 14. doi: 10.1021/ct049976i

（100）Agrawal, P.； Raff, L.； Hagan, M.； Komanduri, R. J. Chem. Phys. 2006， 124, 134306. doi: 10.1063/1.2185638

（101）Manzhos, S.； Carrington, T. J. Chem. Phys. 2006， 125, 084109. doi: 10.1063/1.2336223

（102）Manzhos, S.； Carrington, T. J. Chem. Phys. 2006， 125, 194105. doi: 10.1063/1.2387950

（103）Manzhos, S.； Wang, X. G.； Dawes, R.； Carrington, T. J. Phys. Chem. A 2006， 110, 5295. doi: 10.1021/jp055253z

（104）Behler, J.； Lorenz, S.； Reuter, K. J. Chem. Phys. 2007， 127, 014705. doi: 10.1063/1.2746232

（105）Behler, J.； Parrinello, M. Phys. Rev. Lett. 2007， 98, 146401. doi: 10.1103/PhysRevLett.98.146401

（106）Bholoa, A.； Kenny, S.； Smith, R. Nucl. Instrum. Methods Phys. Res. Sect. B 2007， 255, 1. doi: 10.1016/j.nimb.2006.11.040

（107）Malshe, M.； Raff, L.； Rockley, M.； Hagan, M.； Agrawal, P.；Komanduri, R. J. Chem. Phys. 2007， 127, 134105. doi: 10.1063/1.2768948

（108）Darley, M.； Handley, C.； Popelier, P. J. Chem. Theory Comput. 2008， 4, 1435. doi: 10.1021/ct800166r

（109）Le, H. J. Chem. Phys. 2008， 128, 194310. doi: 10.1063/1.2918503

（110）Malshe, M.； Narulkar, R.； Raff, L.； Hagan, M.； Bukkapatnam, S.； Komanduri, R. J. Chem. Phys. 2008， 129, 044111. doi: 10.1063/1.2957490

（111）Xu, W.； Liu, X.； Luan, S.； Zhang, Q.； Zhang, P. Chem. Phys. Lett. 2008， 464, 92. doi: 10.1016/j.cplett.2008.08.011

（112）Le, H.； Huynh, S.； Raff, L. J. Chem. Phys. 2009， 131, 014107. doi: 10.1063/1.3159748

（113）Pukrittayakamee, A.； Malshe, M.； Hagan, M.； Raff, L.；Narulkar, R.； Bukkapatnam, S.； Komanduri, R. J. Chem. Phys. 2009， 130, 134101. doi: 10.1063/1.3095491

（114）Handley, C.； Popelier, P. J. Phys. Chem. A 2010， 114, 3371. doi: 10.1021/jp9105585

（115）Le, H.； Raff, L. J. Phys. Chem. A 2010， 114, 45. doi: 10.1021/jp907507z

（116）Malshe, M.； Raff, L.； Hagan, M.； Bukkapatnam, S.； Komanduri, R. J. Chem. Phys. 2010， 132, 204103. doi: 10.1063/1.3431624

（117）Behler, J. J. Chem. Phys. 2011， 134, 074106. doi: 10.1063/1.3553717

（118）Behler, J. Phys. Chem. Chem. Phys. 2011， 13, 17930. doi: 10.1039/c1cp21668f

（119）Artrith, N.； Behler, J. Phys. Rev. B 2012， 85, 045439. doi: 10.1103/PhysRevB.85.045439

（120）Jose, K.； Artrith, N.； Behler, J. J. Chem. Phys. 2012， 136, 194111. doi: 10.1063/1.4712397

（121）Raff, L.； Komanduri, R.； Hagan, M. Neural Networks in Chemical Reaction Dynamics； Oxford University Press: New York, 2012.

（122）Hornik, K.； Stinchcombe, M.； White, H. Neural Netw. 1989， 2, 359. doi: 10.1016/0893-6080（89）90020-8

（123）Hagan, M.； Menhaj, M. IEEE Trans. Neural Netw. 1994， 5, 989. doi: 10.1109/72.329697

（124）Sarle, W. Stopped Training and Other Remedies for Overfitting. In Proceedings of the 27th Symposium on the Interface of Computing Science and Statistics； Interface Foundation of North America: Pittsburgh, 1995.

（125）Chen, J.； Xu, X.； Xu, X.； Zhang, D. H. J. Chem. Phys. 2013，138, 154301. doi: 10.1063/1.4801658

（126）Chen, J.； Xu, X.； Xu, X.； Zhang, D. H. J. Chem. Phys. 2013，138, 221104. doi: 10.1063/1.4811109

（127）Li, J.； Chen, J.； Zhang, D. H.； Guo, H. J. Chem. Phys. 2014，140, 044327. doi: 10.1063/1.4863138

（128）Xu, X.； Chen, J.； Zhang, D. H. Chin. J. Chem. Phys. 2014， 27, 373. doi: 10.1063/1674-0068/27/04/373-379

（129）Li, J.； Chen, J.； Zhao, Z. Q.； Xie, D. Q.； Zhang, D. H.； Guo, H. J. Chem. Phys. 2015， 142, 204302. doi: 10.1063/1.4921412

（130）Cohen, A. J.； Mori-Sánchez, P.； Yang, W. Science 2008， 321, 792. doi: 10.1126/science.1158722

（131）Eyring, H.； Polanyi, M. Z. Phys. Chem. Abt. B 1931， 12, 279.

（132）Espinosa-García, J.； Corchado, J. C. J. Phys. Chem. 1996， 100, 16561. doi: 10.1021/jp961608q

（133）Corchado, J.； Bravo, J.； Espinosa-Garcia, J. J. Chem. Phys. 2009， 130, 184314. doi: 10.1063/1.3132223

（134）Espinosa-Garcia, J.； Monge-Palacios, M.； Corchado, J. Adv. Phys. Chem. 2012， 2012, 1. doi: 10.1155/2012/164752

（135）Grant, D. M.； Wilson, P. J.； Tozer, D. J.； Althorpe, S. C. Chem. Phys. Lett. 2003， 375, 162. doi: 10.1016/S0009-2614

（136）Berlie, M.； Roy, D. Can. J. Chem. 1954， 32, 650. doi: 10.1139/v54-086

（137）Wolfgang, R. Annu. Rev. Phys. Chem. 1965， 16, 15. doi: 10.1146/annurev.pc.16.100165.000311

（138）Gray, P.； Herod, A.； Jones, A. Chem. Rev. 1971， 71, 247. doi: 10.1021/cr60271a001

（139）Boyd, R.； Chem. Rev. 1977， 77, 93. doi: 10.1021/cr60305a006

（140）Fernández-Alonso, F.； Zare, R. Annu. Rev. Phys. Chem. 2002，53, 67. doi: 10.1146/annurev.physchem.53.091001.094554

（141）Albu, T.； Espinosa-García, J.； Truhlar, D. Chem. Rev. 2007，107, 5101. doi: 10.1021/cr078026x

（142）Zhang, X. B.； Braams, B.； Bowman, J. J. Chem. Phys. 2006，124, 021104. doi: 10.1063/1.2162532

（143）Zhang, W. Q.； Zhou, Y.； Wu, G. R.； Lu, Y. P.； Pan, H. L.； Fu, B. N.； Shuai, Q.； Liu, L.； Liu, S.； Zhang, L. L.； Jiang, B.； Dai, D. X.； Lee, S. Y.； Xie, Z.； Braams, B.； Bowman, J.； Collins, M.；Zhang, D. H.； Yang, X. M. Proc. Natl. Acad. Sci. U. S. A. 2010，107, 12782. doi: 10.1073/pnas.1006910107

（144）Jiang, B.； Guo, H. J. Chem. Phys. 2013， 139, 054112. doi: 10.1063/1.4817187

（145）Yang, M. H.； Zhang, D. H.； Lee, S. Y. J. Chem. Phys. 2002，117, 9539. doi: 10.1063/1.1524181

（146）Zhang, D. H.； Zhang, J. Z. H. J. Chem. Phys. 1999， 110, 7622. doi: 10.1063/1.478802

Quantum Reaction Dynamics Based on a New Generation Density Functional and Neural Network Potential Energy Surfaces

SU Neil-Qiang1,§CHEN Jun2,§XU Xin1,*ZHANG Dong-H.2,*
（1Department of Chemistry, Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, MOE Key Laboratory of Computational Physical Sciences, Fudan University, Shanghai 200433, P. R. China；2State Key Laboratory of Molecular Reaction Dynamics, Center for Theoretical and Computational Chemistry, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, Liaoning Province, P. R. China）

Recent progresses on a new generation density functional XYG3 and the construction of potential energy surfaces using neural networks are reviewed in this article. Using H3and CH5systems as illustrative examples, it is concluded that highly reliable dynamics results can be obtained from the combination of electronic structure calculations based on efficient and accurate density functionals and accurate potential energy surfaces using neural networks. It holds promise for future applications in larger and more complicated systems.

Density functional; Potential energy surface; Neural network; First principles; Reaction dynamics

O643；O641

10.3866/PKU.WHXB201512011

Received: September 30, 2015； Revised: November 30, 2015； Published on Web: December 1, 2015.

*Corresponding authors. XU Xin, Email: xxchem@fudan.edu.cn； Tel: +86-21-65642032. ZHANG Dong-H., Email: zhangdh@dicp.ac.cn；

Tel: +86-411-84379362.

§These authors contributed equally to this paper.

The project was supported by the National Natural Science Foundation of China （91427301, 91221301, 21433009, 21133004）, National Key Basic Research Program of China （973）（2013CB834601, 2013CB834606）, and Chinese Academy of Sciences.

国家自然科学基金（91427301, 91221301, 21433009, 21133004）, 国家重点基础研究发展规划项目（973）（2013CB834601, 2013CB834606）和中国科学院资助