放射性核素电离空气电子离子对产生率计算

武秀峰，张利峰，马俊平，罗志福

(中国原子能科学研究院 同位素研究所，北京 102413)



放射性核素电离空气电子离子对产生率计算

武秀峰，张利峰，马俊平，罗志福

(中国原子能科学研究院 同位素研究所，北京 102413)

α衰变核素和β衰变核素发射的射线具有电离空气能力而被广泛应用于工业生产中。为研究α或β衰变核素对空气电离能力的大小，本研究采用蒙特卡洛方法模拟理想放射源发出带电粒子在空气中的能量沉积，并结合空气电离理论，计算放射源表面不同距离处电子离子对产生率。利用此计算方法，研究放射源形状、粒子能量、活度和粒子能量分布对电子离子对产生率的影响。结果表明，放射源表面空气中电子离子对产生率的大小主要受放射源活度的影响，而粒子能量及能谱分布等主要影响电离空气范围及电子离子对产生率衰减速率； 3.7×106Bq/cm2的α放射源最大电子离子对产生率可达1011～1012cm-3·s-1量级， 3.7×106Bq/cm2的β放射源最大电子离子对产生率可达109～1010cm-3·s-1量级。研究结果可提供数据支持，为新的放射性同位素应用技术开发提供理论指导。

放射性核素；电离空气；电子离子对产生率；蒙特卡罗方法

α衰变核素和β衰变核素发射出的射线具有电离能力，广泛应用于工业生产中，如静电消除器、离子感烟探头、电子捕获鉴定器、放射性避雷针等[1]。通常利用α或β核素电离空气产生电子离子对，电子和离子在迁移过程中转移电荷达到预期目的。主要应用的核素有210Po、238Pu、241Am、3H、147Pm、85Kr、63Ni、90Sr等。放射性静电消除器[1]研究深入且应用广泛，其原理是α或β核素放射出的α或β粒子电离空气产生电子和正离子对，在消除器周围形成高密度电离云，当带静电荷的物体靠近放射性静电消除器时，消除器和带静电荷的物体间形成电场，在电势的作用下，消除器周围的离子云分布发生变化，并分别被消除器和物体吸附，中和掉物体表面静电，达到消除静电的目的。

目前，已有的研究主要关注放射源电离空气的总能力[2-3]。刘喃喃等[4]通过理论模拟计算分析两种特定核素90Sr-90Y和210Po放射源致空气电离特性，并未对放射源电离空气相关规律进行讨论。研究放射源表面空气被电离的情况随距离变化规律，可为等离子体隐身技术等提供帮助[5]。本研究拟通过计算理想放射源电离空气电子离子对产生率，考察放射源形状、粒子能量、活度和粒子能量分布等的影响，分析理想放射源表面电子离子对产生率随距离的变化规律。

1 模拟计算方法

1.1 蒙特卡罗方法

蒙特卡罗模拟计算方法是以概率统计为理论基础的一种数学计算方法,可真实地模拟实际粒子运动的物理过程，其仿真计算结果与实际结果吻合较好。软件MCNP(Monte Carlo N—Particle transport code)是计算粒子输运过程的一套蒙特卡罗模拟计算软件，用户可以在输入文件中给出计算模型，提供源的属性，感兴区内各种物体的属性，记录粒子信息的方法，进行模拟计算。本研究相关计算选用MCNPX版本，抽样次数为一百万次，用f6卡统计α或β粒子在空气中的能量沉积。

应用于电离空气的α核素主要有238Pu、210Po和241Am，发射的粒子能量分别为5.5 MeV、5.3 MeV和5.5 MeV，本研究中α粒子的能量取值范围为4.5～6.0 MeV；用于电离空气的β核素发射的粒子能量通常不超过2.5 MeV，本研究中β粒子的能量取值范围为0.5～2.5 MeV。

1.2 电子离子对产生率的计算

具有一定能量的带电粒子入射到靶物质中时，与物质原子相互作用，包括与原子核和核外电子发生弹性碰撞和非弹性碰撞，都为带电粒子在原子核和核外电子的库仑场中的作用，带电粒子穿过原子核的库仑位垒与原子核发生核反应需要的粒子能量极高，对于衰变产生的带电粒子可以忽略。带电粒子与原子核或核外电子弹性碰撞中为了满足能量和动量守恒要求，转移能量极少，其中，与原子核的弹性碰撞一般仅在研究物质的辐射损伤中考虑，而与核外电子的弹性碰撞只有能量极低(<100 eV)的β粒子入射到物质中时考虑。带电粒子与原子核的非弹性碰撞中，伴随着带电粒子运动速率和方向的改变发射电磁辐射，但是α粒子质量较大，运动状态改变不大，能量转移可以忽略，β粒子辐射能量损失是一种重要的能量损失机制，转移量与β粒子能量和靶物质的性质有关[6]。

综上所述，α射线与空气作用过程中主要是与空气中原子核外电子作用，导致原子电离或激发，而入射粒子本身的能量逐渐损失。β射线与α射线不同，电子质量小，与空气作用时，主要引起电离能量损失、辐射能量损失和多次散射。辐射损失与电离能量损失之比为：

(1)

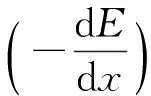
(2)

式中，V为体积；E为带电粒子在体积为V的空间内单位时间沉积的能量；w为入射带电粒子在气体中电离气体产生一对电子离子对需要消耗的平均能量[6]。

1.3 模拟计算

利用2.2节中建立的计算方法，研究放射源形状、粒子能量、活度和粒子能量分布对电子离子对产生率的影响。

2 结果与讨论

2.1 放射源形状的影响

假设存在图1所示的理想的点源、无限长的线源和无限大的面源，为简化研究，假设α放射源和β放射源发射出的粒子均为单能粒子，与源不同距离处空气中电子离子对产生率的变化关系分别示于图2与图3。

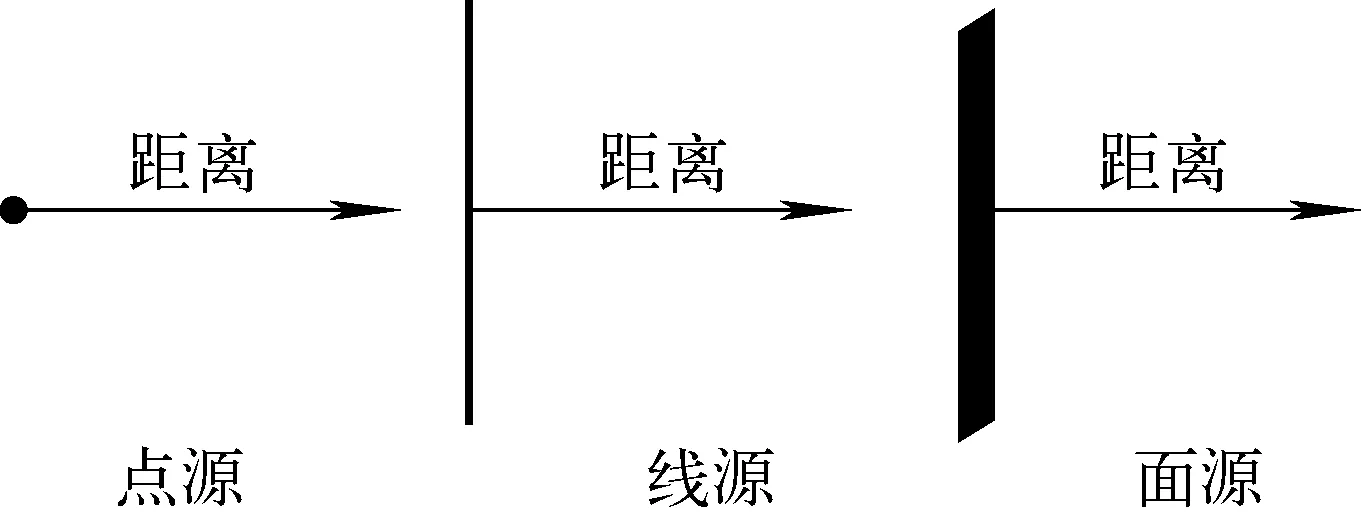
图1 理想放射源形状示意图Fig.1 The diagram of the shape of the source

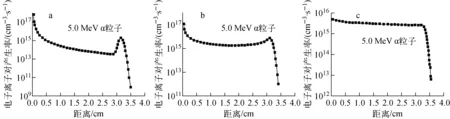
a——3.7×1010 Bq的α点源；b——3.7×1010 Bq/cm的α线源；c——3.7×1010 Bq/cm2的α面源图2 不同形状α放射源的电子离子对产生率随距离变化关系a——3.7×1010 Bq alpha point source；b——3.7×1010 Bq/cm alpha line source；c——3.7×1010 Bq/cm2 alpha non-point sourceFig.2 The relationship between the electron ion pairs production rate and distance of different shapes alpha source

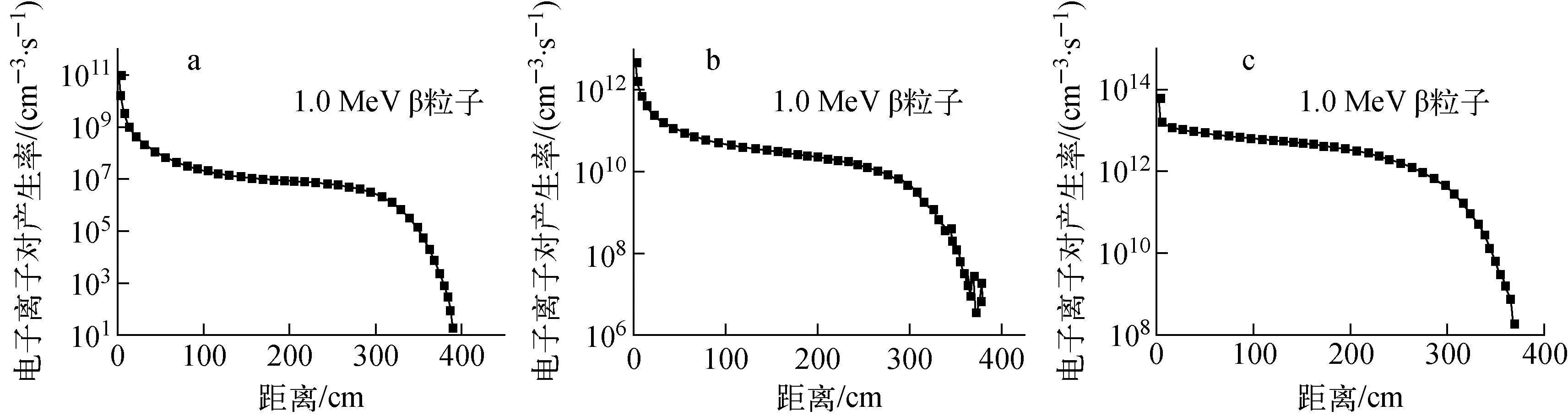
a——3.7×1010 Bq的β点源；b——3.7×1010 Bq/cm的β线源；c——3.7×1010 Bq/cm2的β面源图3 不同形状β放射源的电子离子对产生率随距离变化关系a——3.7×1010 Bq beta point source；b——3.7×1010 Bq/cm beta line source；c——3.7×1010 Bq/cm2 beta non-point sourceFig.3 The relationship between the electron ion pairs production rate and distance of different shapes beta source

图2中点源横坐标是到放射源的距离，对于面源和线源横坐标是到放射源(线或面)的中心垂直距离。由图2可知，由于α粒子质量较大，运动轨迹几乎为直线，随着剩余射程的减少，比电离逐渐增加，在剩余射程的末端即与放射源距离较远处比电离存在Bragg峰，在点源中最明显，在线源和面源中离开中心点发射的射线的Bragg峰出现在垂直线上较近的距离，最后的叠加导致Bragg峰变得不明显甚至消失。由图3可知，由于β粒子质量较小，运动轨迹杂乱，不存在上述现象。对比图2和图3结果可知，α源和β源的点源电子离子对产生率随着距离降低最快，线源次之，面源最慢；α面源电子离子对产生率随距离变化很小，在最大距离处迅速衰减至零，而β面源电子离子对产生率随距离的增加而逐渐减小，最终衰减至零。

2.2 放射源衰变粒子能量的影响

实际应用中更为常见的是面源，此处计算中的放射源均为无限大的理想面源，对3.7×106Bq/cm2的单能α放射源和β放射源计算结果分别示于图4与图5。

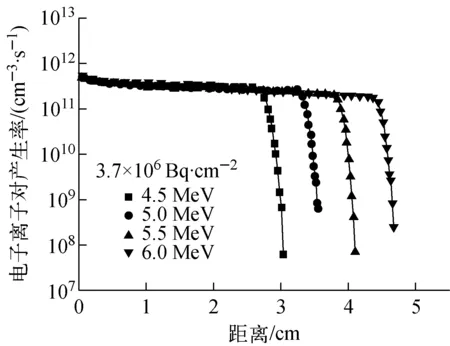
图4 不同能量α放射源的电子离子对产生率随距离变化关系Fig.4 The relationship between the electron ion pairs production rate and distance of different energy alpha source

由图4可知，不同能量的无限大理想α面源表面电子离子对产生率大致相等，随着距离的增加衰减的速率非常小；由于能量不同时，α粒子射程不同，可电离空气的范围随着粒子的能量增加而增加。由图5可知，不同能量的无限大理想β面源表面处电子离子对产生率也大致相等，但是随着距离的增加而快速衰减，粒子能量越高，射程越大，衰减速率越慢。对比图4和图5结果可知，3.7×106Bq/cm2的α放射源最大电子离子对产生率可达1011～1012cm-3·s-1的量级，而3.7×106Bq/cm2的β放射源最大电子离子对产生率为109～1010cm-3·s-1的量级。

图5 不同能量β放射源的电子离子对产生率随距离变化关系Fig.5 The relationship between the electron ion pairs production rate and distance of different energy beta source

2.3 放射源活度的影响

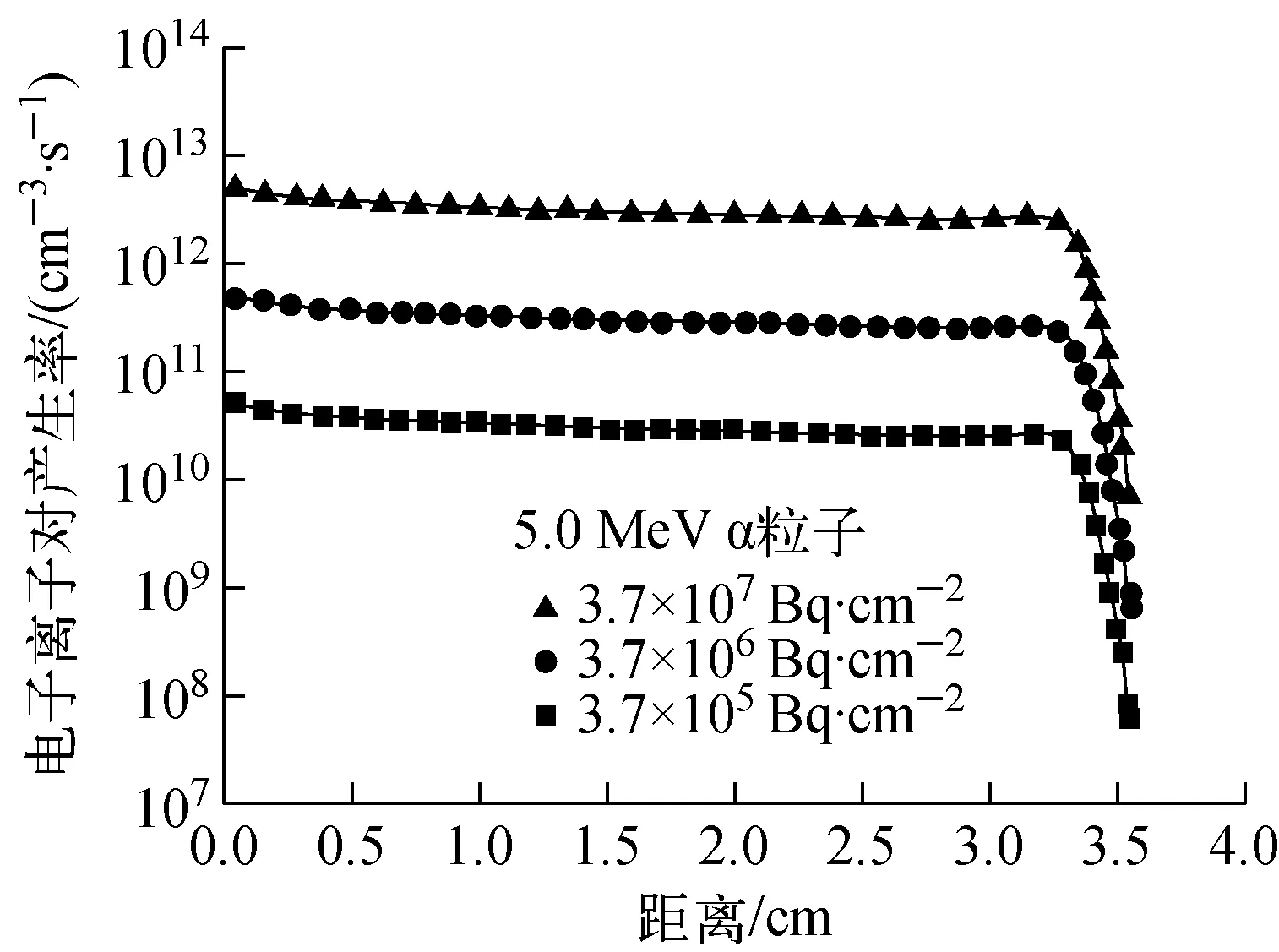
图6 不同活度α放射源的电子离子对产生率随距离变化关系Fig.6 The relationship between the electron ion pairs production rate and distance of different activity alpha source

放射源的活度也会影响在空气中的能量沉积，不同活度的无限大理想α放射源和β放射源面源不同活度计算结果分别示于图6与图7。

图7 不同活度β放射源的电子离子对产生率随距离变化关系Fig.7 The relationship between the electron ion pairs production rate and distance of different activity beta source

放射源在空气中的能量沉积与放射源活度成正比，因此电子离子对产生率也与活度成正比，图6和图7结果与理论预期相符。

2.4 粒子能谱分布的影响

a——单能；；c——Maxwell分布p(E)=E1/2·e-E图8 电子能量分布图a——single energy；；c——Maxwell distribution of p(E)=E1/2·e-EFig.8 Energy spectra of differentelectron steam

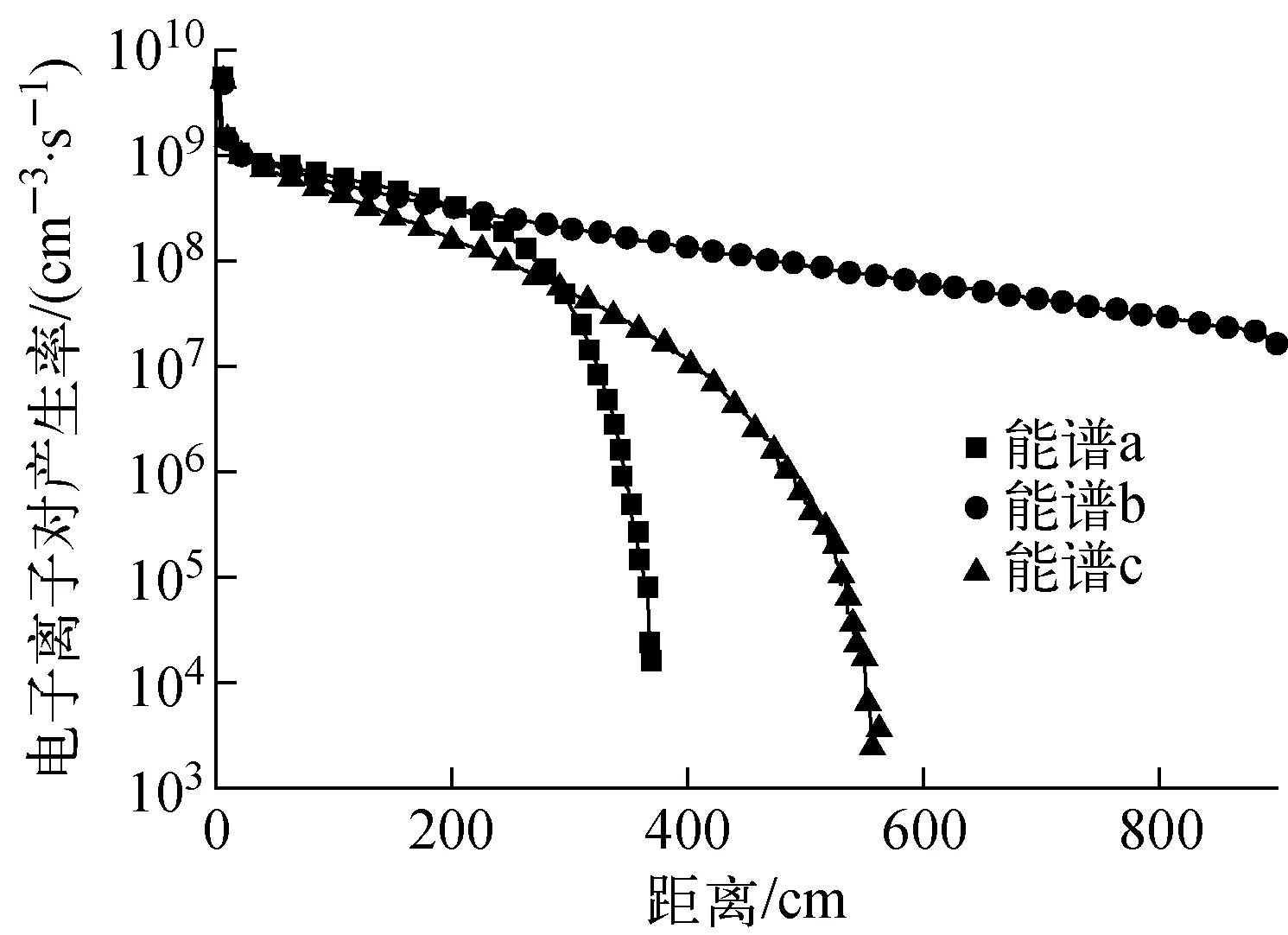
图9 不同活度β放射源的电子离子对产生率随距离变化关系Fig.9 The relationship between the generation of the electron ion pairs and distance of different energy spectra beta source

由图9可知，由于电子分布谱图的不同，电子能量有所差别；在空气中的射程不同，最终影响电离空气的范围，最大电子离子对产生率相差不大。

3 小结

放射源表面空气中电子离子对产生率的大小主要受放射源活度的影响，粒子能量及能谱分布等主要影响电离空气范围及电子离子对产生率衰减速率；3.7×106Bq/cm2的α放射源最大电子离子对产生率可达1011～1012cm-3·s-1的量级，3.7×106Bq/cm2的β放射源最大电子离子对产生率为109～1010cm-3·s-1的量级，但是β放射源可以在更大范围内电离空气产生电子离子对；放射源的形状或面积在一定程度上会影响表面的电子离子对产生率。本研究完善了放射源电离空气的相关规律，并能计算得到一定量的放射性同位素对空气的电离数据，为研究和开发新的放射性同位素应用技术提供参考。

[1] 孙树正. 放射源的制备与应用[M]. 北京：原子能出版社，1992：384-414.

[2] 蔡善钰. 放射性静电消除器在易燃环境中应用评估[J]. 静电，1992，7(2)：22-26.

Cai Shanyu. Evaluation on application of radioisotope static eliminator in flammable atmosphere[J]. Static, 1992, 7(2): 22-26(in Chinese).

[3] 万俊生,杨永青,刘书焕,等. α射线致空气电离的实验研究[J]. 原子能科学技术，2008，42：336-339.

Wan Junsheng, Yang Yongqing, Liu Shuhuan, et al. Experiment studies on atmosphere ionization inducedbya-rays[J].Atomic Energy Science and Technology, 2008, 42: 336-339(in Chinese).

[4] 刘喃喃.90Sr-90Y和210Po放射性源致空气电离特性理论模拟[D]. 西安:西北核技术研究所,2008.

[5] 庄钊文,袁乃昌,刘少斌，等. 等离子体隐身技术[M]. 北京：科学出版社,2005:50-52.

[6] 复旦大学，清华大学，北京大学. 原子核物理实验方法[M]. 北京：原子能出版社，1981:36-38.

Calculation on the Electron Ion Pair Production Rate of the Radioisotope Ionizing Air

WU Xiu-feng, ZHANG Li-feng, MA Jun-ping, LUO Zhi-fu

(DepartmentofIsotope,ChinaInstituteofAtomicEnergy,Beijing102413,China)

The emission of alpha decay and beta decay are widely used in industrial production for its ability of ionizing air. To evaluate the ability of radioisotope ionizing air, a method to calculate the electron ion pair production rate was established. Energy deposition of the ideal radiation source in the air could be obtained through simulating with Monte Carlo method, and then electron ion pair production rate could be calculated. The effect on ionizing air of radiation source shape, energy, activity and particle energy distribution were studied. We found that the electron ion pair production rate was mainly affected by the activity of radioactive source. However, the particle energy and energy spectrum distribution mainly affect the ionization range and the decay rate of the electron ion pair production rate. Computations for a flat surface coated with 3.7×106becquerel alpha radioisotope per square centimeter showed that the largest electron ion pair production rate could be 1011cm-3·s-1to 1012cm-3·s-1, and 109cm-3·s-1to 1010cm-3·s-1for beta radioisotope with the same activity. This conclusion can provide theoretical guidance for existing related application and developing new application of radioactive source.

radioisotope; ionizing air; electron ion pair production rate; Monte Carlo method

2016-05-23;

2016-07-05

TL929

A

1000-7512(2016)04-0198-06

10.7538/tws.2016.29.04.0198