基于高斯过程的大坝变形预测模型

罗亦泳

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.武汉大学 测绘学院，湖北 武汉 430079)



基于高斯过程的大坝变形预测模型

罗亦泳1,2

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.武汉大学 测绘学院，湖北 武汉 430079)

鉴于高斯过程在处理高维数、小样本和非线性等复杂的问题的突出表现，提出基于高斯过程的大坝变形预测新模型.详细分析基于GP的大坝变形预测模型构建过程，并建立预测结果的方差及置信区间的估计方法.将GP模型与多种大坝预测模型进行精度对比，并进行结果可靠性分析.通过实例分析可知，GP模型预测结果的精度指标优于其余方法，并且实测值均在估计的置信区间内.因此，证实GP模型是一种精度及可靠性高的大坝变形预测新方法.

高斯过程；变形预测；精度分析

由于大坝结构特殊，并且大坝建设环境复杂，在其运营期间受到水压力、温度荷载等复杂因素影响，使得大坝产生不同程度的变形，如果变形量超过规定的限制，将对大坝安全运行产生巨大威胁，严重时还可能导致大坝失事，给人民生命财产安全带来巨大危害[1].因此，近年来许多专家学者针对大坝变形数据分析方法进行研究，其中大坝变形预测模型是研究热点内容.建立较为精确的大坝变形预测模型，对及时掌握大坝变形趋势、大坝安全预警具有重要的意义.

当前大坝变形预测模型研究成果较为丰富，主要包括多元回归、时间序列分析、灰色理论、人工神经网络及支持向量机等.大坝变形是一个多因素影响下的非线性复杂过程，因此多元回归、时间序列分析方法较难满足该变形特征，预测效果欠佳.吉培荣等[2]证实，GM(1，1)模型进行预测时要求原始数据序满足指数规律，且数据序列变化不能太快，否则预测精度较差.王新洲等[3-11]基于智能算法BP神经网络、支持向量机模型构建变形预测模型，这些方法有效改善变形预测模型的精度.但是BP神经网络存在结构设计难、容易陷入局部最优等问题，支持向量机的参数确定及核函数选择较为困难.针对以上变形预测模型存在的不足，刘开云等[12-14]将高斯过程算法应用于隧道围岩、滑坡的变形预测，并取得较好的精度，但该算法应用于大坝变形预测研究较少.因此，笔者基于高斯过程机器学习算法构建一种参数自适应、具有概率解释的大坝变形预测新模型，并建立结果可靠性分析方法.通过实例分析，验证新模型的精度及可靠性.

1 高斯过程学习理论

2006年由Rasmussen等从机器学习的核方法角度出发正式提出高斯过程机器学习方法(Gaussian process, GP)[15].该方法能很好地处理高维数、小样本、非线性等复杂的问题.GP的参数全部由算法本身估计，不需要用户确定参数，实现GP参数自适应，大大降低算法的在实际使用中的复杂性.并且模型可对预测输出做出概率解释，分析模型的可靠性.因此，该模型在许多领域都得到较好的应用.

f(X)～GP(m(X),WK(X,X))

(1)

式中：m(X)为GP均值函数；K(X,X′)为协方差函数[16-17].

数据集S的t为受加性噪声污染的模型输出观测值，则t表示为

t=f(X)+ε

(2)

因此，可推导t的分布为

(3)

其中In为n阶单位矩阵.对于新的输入X*，模型对应的输出为t*.因此，t与t*的联合概率分布为

(4)

根据贝叶斯估计原理和联合正态分布的条件概率特性，推导预测值t*的后验概率分布为[18]

(5)

(6)

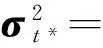
(7)

因此，GP模型构建即利用训练数据集根据贝叶斯原理求取超参数θ的最大后验似然估计值.GP模型通过建立训练样本条件概率的负对数似然函数，对超参数求偏导，采用共轭梯度优化方法自适应确定GP模型的最优超参数解，最终基于最优超参数构建高斯过程回归模型.由GP算法的实现过程可知，对于小样本数据，GP模型计算量不大.但是当样本数据较大时，GP模型存在计算负担较重的问题，需要从超参数求解方法进行改进，以提高计算效率.

2 模型构建及结果分析

2.1 大坝变形预测模型建立

大坝变形预测模型建立即构建变形变量与变形影响因素之间复杂非线性函数关系.通过查阅大坝变形影响因素相关文献，确定大坝影响因素主要包括上游水位H、观测当日的温度T及观测日期t.因此，以H，T，t为GP模型输入变形，大坝水平位移量Y为GP模型输出，模型通过对训练数据集的学习，构建大坝预测模型.以广州蓄能水电厂的下库大坝为例开展大坝变形预测模型研究，下库坝坝型是碾压混凝十重力坝，坝顶高程为294 m，防浪墙顶高程为291 m.坝顶长为153.12 m，大坝最大坝高为43.5 m，坝顶宽度为7 m，坝底最大宽为33.18 m.研究以广蓄电厂下水库坝的河床坝段的2#观测点为例，获得2000年4月12日至2003年4月16期间的坝顶水平位移量Y，T，t数据，并经过数据预处理获得64期大坝变形数据，具体数据参考文献[10-11]，详细模型建立步骤如下：

1) 建模数据准备. 以1～50期大坝变形观测数据建立训练集S={Xi,Yi}，Xi=[Hi,Ti,ti]，i=1，2，…，50.以51～64期大坝变形观测数据建立测试集，D={Xj,Yj}，Xj=[Hj,Tj,tj]，j=51，52，…，64.将数据去掉量纲的影响，对训练数据集、测试集进行归一化，归一化公式为

(8)

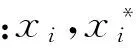
2) GP预测模型建立.选择协方差函数K(X,X)，确定模型超参数解算方法.基于文献[15]对协方差函数的分析结果，最终选择Materniso协方差函数，采用共轭梯度优化方法，搜索模型的超参数最优解.训练数据集S训练GP算法，自适应解算模型超参数.将超参数代入式(6，7)，建立基于GP的大坝变形预测模型，可获得大坝变形预测值及方差.

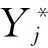
(9)

(10)

(11)

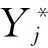
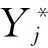
(12)

2.2 结果分析

GP模型通过对训练集S={Xi,Yi}的学习，自适应解算出GP模型的超参数向量为θ=[-9.1221，-9.4563，-3.7463，-9.7427，0.1354].利用超参数向量θ可建立大坝预测的GP模型，计算51～64期大坝的预测值及对应方差，具体计算结果见表1所示.

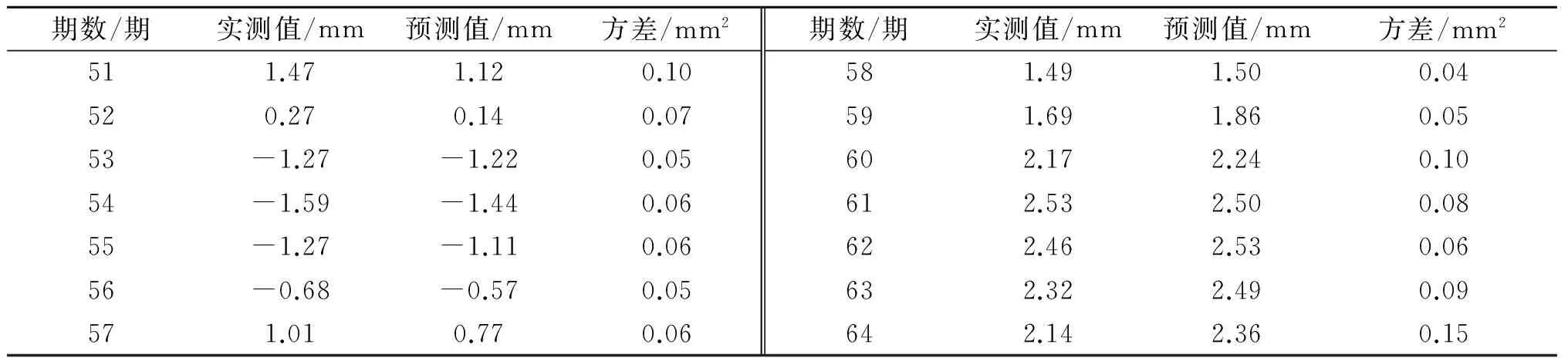
表1 GP模型大坝变形预测结果

为验证GP模型精度的优劣，同时采用BP神经网络、灰色支持向量机(GM-SVM)和经验模态分解支持向量机(EMD-SVM)等方法构建大坝变形预测模型，具体建模方法参见文献[10-11].笔者采用平均绝对误差、平均相对误差、均方根误差等精度指标对大坝变形预测模型精度进行对比分析，证实GP模型具有较高的大坝变形预测精度，各大坝变形预测模型具体精度指标如表2所示.

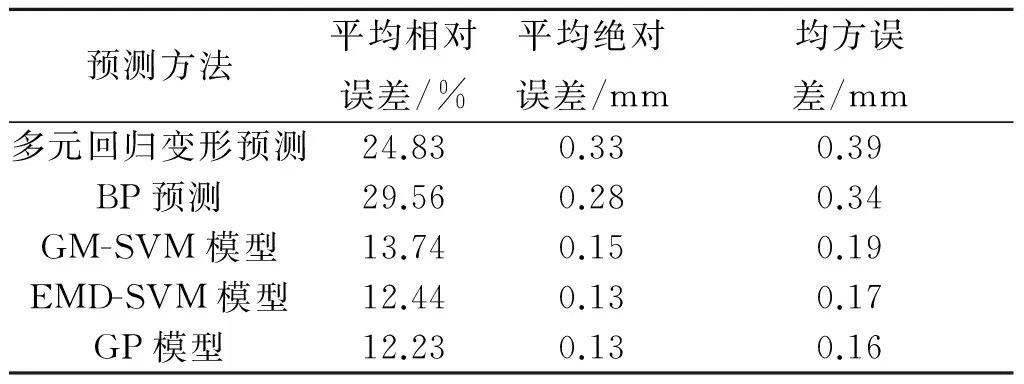
表2 大坝变形预测结果精度

由表2可知：GP模型、支持向量机的改进模型(GM-SVM模型、EMD-SVM模型)的大坝变形预测的MAE，MRE，RMSE精度指标均较大程度优于BP及多元回归模型，并且GP模型的精度指标略优于支持向量机的改进方法.GP模型在建模过程中不需要用户设置各类参数，GP模型参数均自适应求解.因此，可有效避免神经网络、支持向量机等方法由于模型参数设置不合理而影响预测精度的问题.综上所述，证实基于GP的大坝变形预测模型具有优秀的精度，并且算法使用简单.

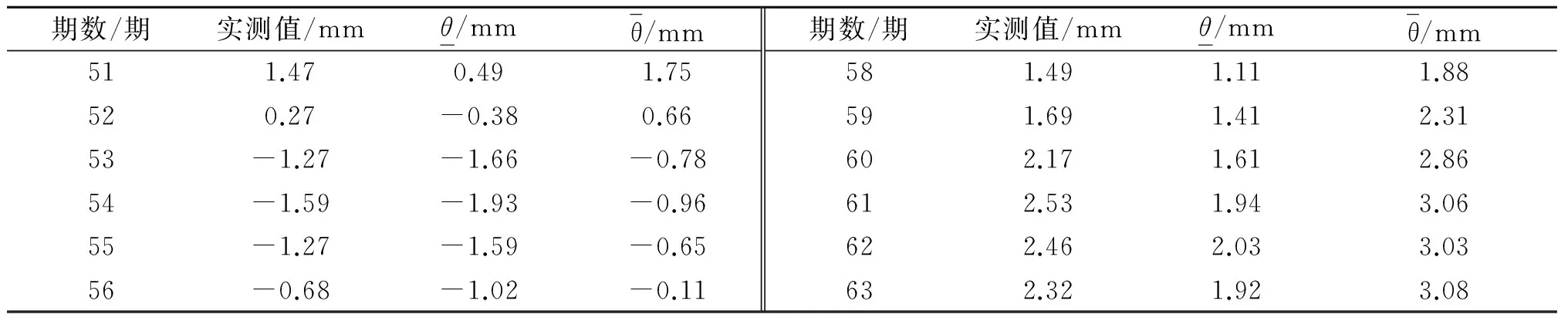
表3 基于GP模型估计的置信区间上、下界

根据GP模型估计的51～64期大坝变形变量的均值(即大坝变形预测值)及方差，将均值及方差代入置信区间估计式(12)，求解51～64期大坝变形变量的置信区间上、下界，具体结果见表3.由表3可知：51～64期大坝变形变量的实测值均在置信区间上、下界范围内.因此，可以证明基于GP的大坝变形预测模型结果具有很高的可靠性，为成果的实际使用提供理论依据.

3 结 论

基于高斯过程模型构建大坝变形预测新方法，较为详细的分析模型构建过程.通过与多种大坝变形预测模型进行精度对比，并且进行置信区间分析，结果表明：大坝变形预测的GP方法在建模过程中不需要用户确定参数，有效提高模型的稳定性及实用性.GP模型的MAE，MRE，RMSE精度指标总体优于多元回归、BP网络和支持向量机改进模型，具有较高的大坝变形预测精度；GP模型在获得高精度预测结果的同时，可估计大坝变形量的方差、置信区间等可靠性分析数据.通过GP模型对测试集预测结果的置信区间分析，实测大坝变形量均在对应置信区间内，证实新方法结果的可靠性高.

[1] 吴中如.水工建筑物安全监控理论及其工程应用[M].北京:高等教育出版社,2003.

[2] 吉培荣,黄巍松,胡翔勇.灰色预测模型特性的研究[J].系统工程理论与实践,2001(9):105-108.

[3] 王新洲,邓兴升.大坝变形预报的模糊神经网络模型[J].武汉大学学报(信息科学版),2005,30(7):588-594.

[4] 孟凡丽,郑棋,李燕,等.基于BP神经网络的深基坑围护变形预测[J].浙江工业大学学报,2014，42(4):367-372.

[5] 吴云芳,李珍照.大坝神经网络预报模型与大坝回归预报模型的比较[J].长江科学院院报，2003,20(2):50-53.

[6] 马丽霞,王凤艳,王静.基于matlab工具箱的神经网络在大坝变形区间预报中的应用[J].测绘通报,2010(5)：35-38.

[7] 徐锋，王崇倡，张飞.粒子群-BP神经网络模型在大坝变形监测中的应用[J].测绘科学,2012,37(4):181-184.

[8] 王新洲,范千,许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报(信息科学版),2008,33(5):469-472.

[9] 宋志宇,李俊杰.基于混沌优化支持向量机的大坝安全监控预测[J].武汉大学学报(工学版),2007,40(1):53-58.

[10] 张豪，许四法.基于经验模态分解和遗传支持向量机的多尺度大坝变形预测[J].岩石力学与工程学报,2011,30(增2):3681-3689.

[11] 罗亦泳,张豪.基于遗传支持向量机的多维灰色变形预测模型研究[J].浙江工业大学学报,2010,38(1):79-64.

[12] 刘开云,刘保国,徐冲.基于遗传-组合核函数高斯过程回归算法的边坡非线性变形时序分析智能模型[J].岩石力学与工程学报,2009，28(10):2128-2134.

[13] 雷鸣.基于高斯过程的变形预测算法研究[D].南昌：东华理工大学,2013.

[14] 刘开云,方昱,刘保国,徐冲.隧道围岩变形预测的进化高斯过程回归模型[J].铁道学报,2011,33(12):101-106.

[15] RASMUSSEN C E, WILLIAMS K. Gaussian process for machine learning[M]. Cambridge: The MIT Press,2006.

[16] SNELSON E. Flexible and efficient Gaussian process models for machine learning[D]. London:Gatsby Computational Neuroscience Unit,University of London,2007.

[17] KOCIAN J,AZMAN K. Gaussian process model identification:a process engineering case study[J].Systems science,2008,34(3):31-38.

[18] 胡明.基于高斯过程的非线性预测控制[D].广州：华南理工大学,2012.

[19] 罗亦泳,张豪.基于自适应进化相关向量机的耕地面积预测模型[J].农业工程学报,2015,31(9):257-265.

[20] 盛骤，谢式千，潘承毅.概率论与数理统计(新版)[M].北京：高等教育出版社，2010.

(责任编辑：刘 岩)

A Gaussian process based model for predicting deformations of dams

LUO Yiyong1,2

(1.Faculty of Geomatics， East China University of Technology， Nanchang 330013， China;2.School of Geodesy and Geomatics, Wuhan University， Wuhan 430079， China)

In view of the excellent performance of the Gaussian process model in dealing with complicated problems of high dimensions, small samples, and nonlinearity, a Gaussian process based model is proposed for predicting the deformations of dams. The Gaussian process based model for predicting the deformations of dams is analyzed in detail and an estimation method for the variance and the confidence interval is proposed. The Gaussian process based method is compared with a few prediction models for dams and a reliability analysis of numerical results is conducted. Verification examples show that the Gaussian process based method has a higher computational accuracy than other methods and the measured values are all within the confidence interval. Therefore, it is validated that the Gaussian process based model is a new prediction method for the deformations of dams with high accuracy and reliability.

Gaussian process; deformation prediction; accuracy analysis

2016-01-25

国家自然科学基金资助项目(41374007)；江西省自然科学基金资助项目(20151BAB213031);江西省教育厅科学技术研究项目(GJJ150592)

罗亦泳(1982—)，男，江西抚州人，讲师，博士研究生，主要从事变形数据分析研究，E-mail：luoyiyong@whu.edu.cn.

P258

A

1006-4303(2016)05-0543-04