面向层级结构的任务动态分配策略
2016-11-18臧立涛李澎林
李 伟,臧立涛,李澎林
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
面向层级结构的任务动态分配策略
李 伟,臧立涛,李澎林
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
当前的任务分配策略主要考虑了候选者的个体属性,而忽略了候选者下属资源对任务分配的影响.针对企业层次化的组织结构特点,提出一种面向层级结构的任务动态分配策略,充分考虑了层级结构下任务候选者拥有的人力资源对任务分配的影响,给出了基于该策略的可量化候选者属性适配度计算方法,并改进了传统的能力适配度计算方法.仿真实验结果表明:考虑了下属资源的任务动态分配模型进一步提高了任务分配的适应性,分配结果更加符合预期.
层级结构;任务动态分配;能力适配度;工作流管理
工作流技术一直是计算机和企业自动化管理领域研究的热点之一,其中工作流任务分配策略一直是其中重要研究内容.工作流任务分配策略主要解决在流程的运行过程中,将合适的任务在合适的时机分派给合适的人[1].在现代企业管理中,企业在组织管理方面遵循层级结构,任务往往交由组织中的一个团队完成,所以,在研究任务分配策略时需充分考虑到层级结构对任务分配的影响.
任务动态分配的一个研究重点是人员与任务执行过程中各实体的解耦,通过引入角色的概念[2-3]以及规则定义工具[4-5]可以增加任务分配的柔性,角色是任务分配的具体实体,而与角色对应的人员可以动态变化.任务动态分配另一个研究重点是当候选者角色多于1人时,如何将任务分配给最合适的候选人.吕炎杰等[6]通过模糊集理论和知识相似度解决分配匹配问题.马嵩华等[7]在任务分配时考虑有限人员下对分配者的能力经验进行描述.LIANG等[8]从任务分配影响因素着手,在评估匹配度时使用候选者属性的三角模糊数来代替精确值.肖郑进等[9]在LIANG研究基础上综合考虑候选人能力,经验,负载,成功率,弹性,给出了任务分配多级模型.余阳等[10]在任务分配时考虑到候选者社会关系的影响,丰富了任务分配影响因素.任务分配多级模型可以动态扩充和精简,适合各种复杂的分配场景,但仍然存在以下问题:1) 企业组织结构有层级性,任务分配多级模型没有考虑到候选者下层的人力资源,而只考虑了候选者个体属性.2) 任务分配多级模型在计算候选者能力适配度时能力越高得分越高,会使能力高的候选者总比能力低的候选者优先分配到任务.所以在任务分配多级模型基础上,引入了企业组织中上下级协同概念,提出面向层级结构的任务分配多级模型.基于模型改进了能力适配度计算方法,匹配到能力刚好满足任务要求,又不超出任务要求的候选人.
1 面向层级结构的任务分配多级模型
传统的任务分配多级模型需要逐级计算候选者每一项分配影响因素与任务的适配分数,然后对每一项因素的适配分数加权求出最终的任务适配分数,在该模型中,候选者都是个体.而在面向层级结构的任务分配多级模型中,除了需要考虑候选者个体与任务的适配情况外,还需要考虑候选者与下属形成的协同圈与任务的适配情况.基于该设想,提出了一种面向层级结构的任务分配多级模型,如图1所示.

图1 面向层级结构的任务分配多级模型Fig.1 Dynamic distribution of task for hierarchial structure model
在该模型下,候选者除了个体外还有可能是多个个体形成的协同圈,协同圈由候选个体及其下属组成,他们协同地完成同一个任务目标.此时,协同圈将成为任务分配的候选元素,再考虑任务分配时,协同圈内部个体均参与任务适配度计算,根据各个个体,同样需要对协同圈的各项适配分数进行计算.
2 面向层级结构的任务动态分配策略
基于前述的面向层级结构的任务分配多级模型,假设分配者有待分配任务J,分配者存在2个直接下属X和Y,X存在两个下属A和B,Y存在一个下属C,X与Y可以和各自下属构成协同圈{X,A},{X,B},{X,A,B},{Y,C},面向层级结构的任务动态分配策略流程如图2所示.具体流程描述如图2所示.

图2 任务分配流程图Fig.2 Task distribution progress
1)确定任务分配候选集.任务分配者的直接下属构成分配的显式候选集{X,Y},考虑到X,Y存在下属可供调配,所以X,Y与各自下属形成的协同圈构成任务分配的隐式候选集{{X,A},{X,B},{X,A,B},{Y,C}},显示候选集和隐式候选集的合集构成分配的总候选集.
2)计算候选集中每一个元素的能力适配值.记待分配任务为J,完成J需要k种技能Cn,(n=1,2,…,k),J对技能Cn的要求为w(J,Cn).个体u的能力集合可以使用一组二元组的集合表示,即Cap(u)=<(C1,L1),…,(Cn,Ln)>,其中Cn表示能力名,Ln表示u对应能力Cn所具有的能力评估级数,级数越高表示能力越强.隐式分配候选集每一个元素是i个个体形成的协同圈P,记为Coop(P),P={U1,U2,…,Ui}则Cap(Coop(P))=<(C1,Max(L11,L21,…,Li1)),…,(Cn,Max(L1n,L2n,…,Lin))>,Lin表示协同圈中的个体Ui的Ln.假设完成任务需要的能力集合为Taskcap(J)=<(C1,JL1),…,(Cn,JLn)>,JLn=w(J,Cn),候选元素Ui对应J的能力集合为Cap(Ui,J)=<(C1,Li),…,(Cn,Ln)>,记Ui执行任务J的能力溢出值为Spill(Ui,J),计算式为
(1)Ui执行任务J的能力适配值为Capfit(Ui,J),计算式为
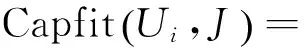
(2)
减去能力溢出值是为了确保候选元素能力评估级数与任务需要的能力要求一致时得分最高.
3)计算候选集中每一个元素的经验适配值.为了计算候选元素Ui相对于任务J的经验值,需要对Ui最近一个时间段内执行过的历史数据进行统计.
假设完成J需要的能力集合为Taskcap(J)=<(C1,JLi),…,(Cn,JLn)>,个体u在近期内执行的n个任务的集合为Jr(u)={Jr1,Jr2,…,Jrn},使用M(Jr(u),Cn)表示历史任务集合Jr(u)中的任务对技能Cn要求最高的值,统计J中各项技能Ci在Jr(u)中出现的最高值,可以得到u相对J的历史最高能力集合Caphistory(u,j)=<(C1,HLi),…,(Cn,HLn)>,HLn=M(Jr(u),Cn).如果候选元素是协同圈P,则Caphistory(P,j)=<(C1,Max(HL11,…,HLi1)),…,(Cn,Max(HL1n,…,HLin))>,HLin表示协同圈中第i个人员的HLn,当候选元素Ui的HLn高于任务J对技能Cn的要求时,可以认为就技能Cn而言,Ui最近执行过的任务经验完全适用,所以经验值为1;当HLn低于任务J对技能Cn的要求时,Ui执行过的任务相对于任务J的经验可表示为二者能力需求的比值,候选元素Ui近期执行的任务相对于任务J的经验值Exp(Ui,J)定义为
(3)
4)计算候选集中每一个元素的绝对负载.同一个任务对于不同参与者所需要的执行时间是不同的,如果以任务数量来衡量参与者负载就会导致伪负载平衡,所以最好以参与者的执行时间作为负载平衡指标.如果个体u当前工作列表中待执行的工作项共有r个,则u的任务负载描述可以使用一组二元组来表示,即Wol(u)=<(J1,T1),…,(Jn,Tn)>,其中Jn表示工作流任务列表中待执行的工作项,而Tn表示u完成此工作项预期的工作时间.所以对于u而言,他的绝对负载的定义为
(4)如果候选元素是协同圈P,则P的绝对负载计算式为
(5)
5)计算每一个元素的能力适配分数,经验适配分数,负载分数.任务候选集U(U={U1,U2,…,Un})的每一个元素都有能力适配值,经验适配值,绝对负载三个评估值,如果要综合考量必须进行数值归一化[11],得出每个评估因素的评估分数.
归一化处理后能力适配分数Scap(Ui,J)为
(6)
归一化处理后经验适配分数Sexp(Ui,J)为
(7)
归一化处理后负载分数Sload(Ui)为
(8)
6)计算候选集中每一个元素的综合适配分数.不同任务有不同的侧重点,有些要求参与者有很高的技能水平,有些要求参与者有丰富的经验,而有些需要参与者有充足的时间,所以需要引入权重来衡量不同的影响因素[12-13],分别用Kcap,Kexp,Kload表示能力,经验,负载的影响权重,权重取值在[0,1]之间,且Kcap+Kexp+Kload=1,数值越大,说明此项因素影响最大.每个候选元素Ui的综合适配分数S(Ui,J)定义为
S(Ui,J)=KcapScap(Ui,J)+KexpSexp(Ui,J)+
KloadSload(Ui)
(9)
7)根据综合评估分数对候选集的元素进行降序排序,排序后越靠前的元素与任务的适配度越高,被分配的机会越大.
3 典型实例分析
软件产品开发项目中的人力资本十分昂贵,将开发任务分配给合适的人员尤为重要,下面以软件产品开发管理项目中的一个典型过程为例来说明任务分配机制.整个任务对开发者的前端开发能力(Front)要求为3,服务器开发能力(Server)要求为7,数据库开发能力(Database)要求为5,任务分配者U有U1,U2两名下属可供分配,U1有U11,U12两名下属,U2有U21一名下属.他们相对开发任务的能力集,历史最高能力集,负载如表1所示,任务中能力,经验,负载的权重分别是0.5,0.3,0.2.

表1 任务候选者及其下属能力、历史最高能力、负载说明
使用传统的任务分配多级模型分配此项任务,计算的能力适配分数,经验适配分数,负载分数和综合适配分数如表2所示.

表2 传统的任务分配多级模型适配度计算结果
使用面向层级结构的任务分配模型分配此项任务,计算的能力适配分数,经验适配分数,负载分数和综合适配分数如表3所示.
表3 面向层级结构的任务分配多级模型适配度计算结果
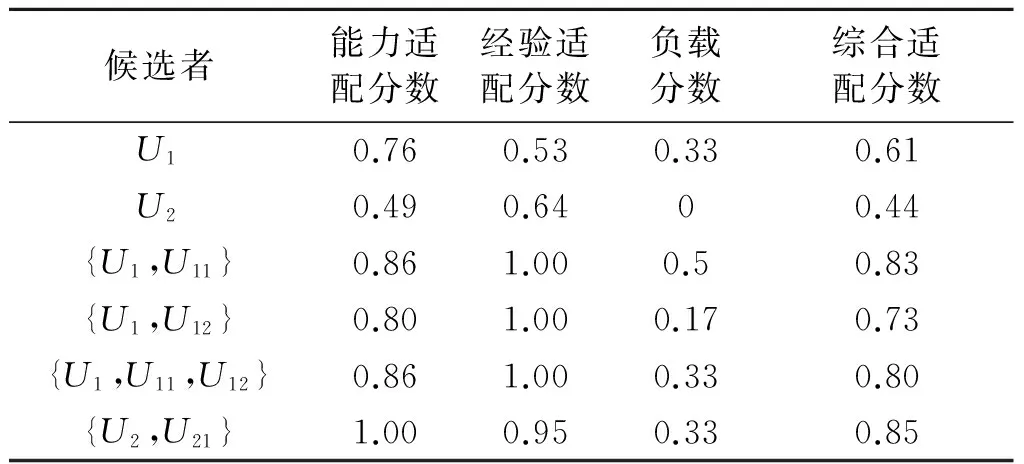
Table 3 Dynamic distribution of task for hierarchial structure model calculate result
分析结果可知:传统的任务分配模型只考虑到显式候选集{U1,U2},比较U1和U2可以发现U1的能力比U2更接近任务要求,且U1的负载也低于U2,因此U1的适配分数高于U2,现象与结果一致,但是此模型只考虑了U1和U2的个体属性而忽略了下属资源对分配的影响.面向层级结构的任务分配模型充分考虑了候选者的下级员工,U1,U2可以调度下属,与下属构成协同圈,观察数据可知U2和下属U21构成的协同圈与任务能力要求最接近,模型计算出的适配度也最高,所以优先把任务分配给U2,这样的分配结果与实际预期更加吻合.
4 结 论
研究了层级结构下任务动态分配问题.通过引入上下级协同圈的概念提出了面向层级结构的任务分配多级模型,新模型扩充了传统的任务分配多级模型的分配候选集,并对能力适配度计算方法进行了改进,新算法可以使能力值最接近任务要求的候选者得到的能力适配分数最高,同时给出了协同圈和候选个体分配影响因子的计算方法.通过仿真实验可知,在层级结构的组织中使用面向层次结构的任务分配模型可以适配到更适合的候选者.
[1] 王建民,尹建伟,窦万春.业务过程管理技术专题前言[J].软件学报,2015,26(3):447-448.
[2] AALST W M P V D, KUMAR A.A reference model for team-enabled workflow management systems[J].Data & knowledge engineering,2001,38(3):335-363.
[3] 张晓光,曹健,张申生.策略约束面向角色和团队关系的工作流任务分配管理[J].计算机研究与发展,2002,39(12):1556-1563.
[4] 李春芳,谭庆平,徐建军,等.基于业务规则的工作流任务分派设计与实现[J].计算机工程与设计,2008,29(21):5572-5575.
[5] 唐达,杨元生.基于层次细化Petri网的工作流参与者机制与动态特性研究[J].计算机研究与发展,2004,41(9):1545-1553.
[6] 吕炎杰,赵罡,于勇.基于模糊集理论和知识相似度的复杂产品设计任务分配方法[J].计算机集成制造系统,2015,21(4):904-913.
[7] 马嵩华,田凌.面向中小企业有限人员的经验任务分配策略[J].计算机集成制造系统,2014,20(9):2297-2304.
[8] LIANG G S,WANG M J J.Personnel placement in a fuzzy environment[J].Computers & operations research,1992,19(2):107-121.
[9] 肖郑进,何钦铭,陈奇.模糊环境中工作流任务分配的多级模型[J].计算机研究与发展,2007,44(2):302-309.
[10] 余阳,王颍,刘醒梅,等.基于社会关系的工作流任务分派策略研究[J].软件学报,2015,26(3):562-573.
[11] 陈鲤江,景程,吴姚鑫,等.数学表达式的归一化方法研究[J].浙江工业大学学报,2012,40(2):229-232.
[12] 徐兴,李仁旺,吴新丽,等.面向供应链协同的供应商选择模型的研究[J].浙江工业大学学报,2011,39(5):550-554.
[13] 何荣军,卢艳,王钧,等.基于AHP模糊评价法在草菇蛋卷研制中的应用[J].浙江工业大学学报,2015,43(1):73-76.
(责任编辑:刘 岩)
The strategy of task dynamic distribution for hierarchical structure
LI Wei, ZANG Litao, LI Penglin
(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)
The current task allocation algorithm is mainly emphasized in the user role when considering the factor of task allocation, but the impact of the candidate’s subordinates resources on the assignments is ignored. Focusing on the structural feature of enterprise organizational hierarchy, a task dynamic allocation strategy oriented hierarchy is proposed. In this method, the candidate’s human resources are taken account fully and a quantifiable calculation method for candidate attribute adaptation based on this strategy is given. This quantifiable calculation method has improved the traditional method. The simulation results show that the new method further improves the fitness of task allocation and the allocation results are more in line with expectations.
hierarchial structure; task assignment; capacity fitness; workflow management
2016-01-29
李 伟(1976—),男,河南信阳人,副教授,研究方向为移动互联网、CSCW和地理信息系统,E-mail:liwzjut@zjut.edu.cn.
TP311
A
1006-4303(2016)05-0501-04
