含孔洞的颗粒增强复合材料力学性能研究

许杨剑,武鹏伟,许 雷,梁利华

(浙江工业大学 机械工程学院，浙江 杭州 310014)



含孔洞的颗粒增强复合材料力学性能研究

许杨剑,武鹏伟,许 雷,梁利华

(浙江工业大学 机械工程学院，浙江 杭州 310014)

研究了颗粒体积分数、粒径、材料特性和孔洞等因素对颗粒增强复合材料的影响.通过编程实现了二维RVE模型构建，并给出了周期性位移边界条件施加过程.基于ABAQUS二次开发实现均匀化方法，并用该方法计算分析了RVE的力学响应.研究表明：软化颗粒比增强颗粒对基体力学性能的影响范围大，孔洞缺陷对基体的力学性能具有严重的削弱作用.

复合材料；均匀化；代表性体积单元；周期性边界条件

颗粒增强复合材料是通过在基体材料中添加增强颗粒而形成的，其具有许多优良的性能，被广泛应用于航天、国防和汽车等工程领域.由于制造过程易产生孔洞等缺陷，其细观结构较为复杂，所以目前对其力学性能的研究大多采用细观力学分析方法.其中，基于代表性体积单元(RVE)的均匀化方法是一种能有效反映复合材料宏观力学性能与组分材料细观结构参量间关系的细观力学分析方法[1-2].Segurado等[3]通过有限元法研究了增强颗粒分布对RVE拉伸加载时力学性能的影响.李伟等[4]研究了增强颗粒粒径分布对复合材料力学性能的影响，建立了一个粒子统计分布的细观等效力方法.崔文凯等[5]提出了一种复合材料单胞模型生成和网格划分算法，但其边界上颗粒没有按照周期性分布.El等[6]研究了不同颗粒形状对RVE的等效参数的影响，并给出了等效参数随颗粒含量变化的函数.Spaggiari等[7]利用有限元法研究了含有球形和椭圆形孔洞聚合物基复合材料，表明孔洞含量比孔洞分布对基体的影响大.有限元软件ABAQUS因具有较好的二次开发能力及非线性求解功能，而得到广泛的应用[8-10].

针对RVE模型的不足之处，通过Fortran编程构建含颗粒/孔洞的RVE模型，并对其施加周期性边界条件(PBC).目前，均匀化计算多数是基于非商业有限元程序进行计算分析的，大大阻碍了该方法的发展和应用.针对这一问题，基于ABAQUS计算平台，应用多个用户自定义程序接口，实现均匀化计算，并系统地研究了含孔洞的颗粒增强复合材料在不同状况下的力学响应，对于颗粒增强复合材料的设计提供一定的借鉴作用.

1 RVE建模

复合材料细观结构上颗粒或孔洞形状，大小和分布均具有很大的随机性.采用Fortran语言编程实现随机生成不同直径的圆形颗粒或孔洞，亦可以生成同一大小直径的颗粒或孔洞，且随机分布的二维RVE模型.快速生成RVE的流程，如图1所示.

在RVE中，含颗粒或孔洞生成过程区别在于在ANSYS中基体和颗粒之间进行不同的布尔操作.RVE模型的边界上有颗粒分布，且颗粒呈周期性分布，RVE有限元模型划分对称网格便于施加PBC(注：PBC的施加详见后文).图2显示了构造的颗粒20%孔洞5%RVE有限元模型.值得注意的是在RVE区域内投放颗粒或孔洞的位置与随机数有关，编程产生的随机数与时间无关.因此，当模型参数确定时，生成的颗粒或孔洞分布情况是确定的.

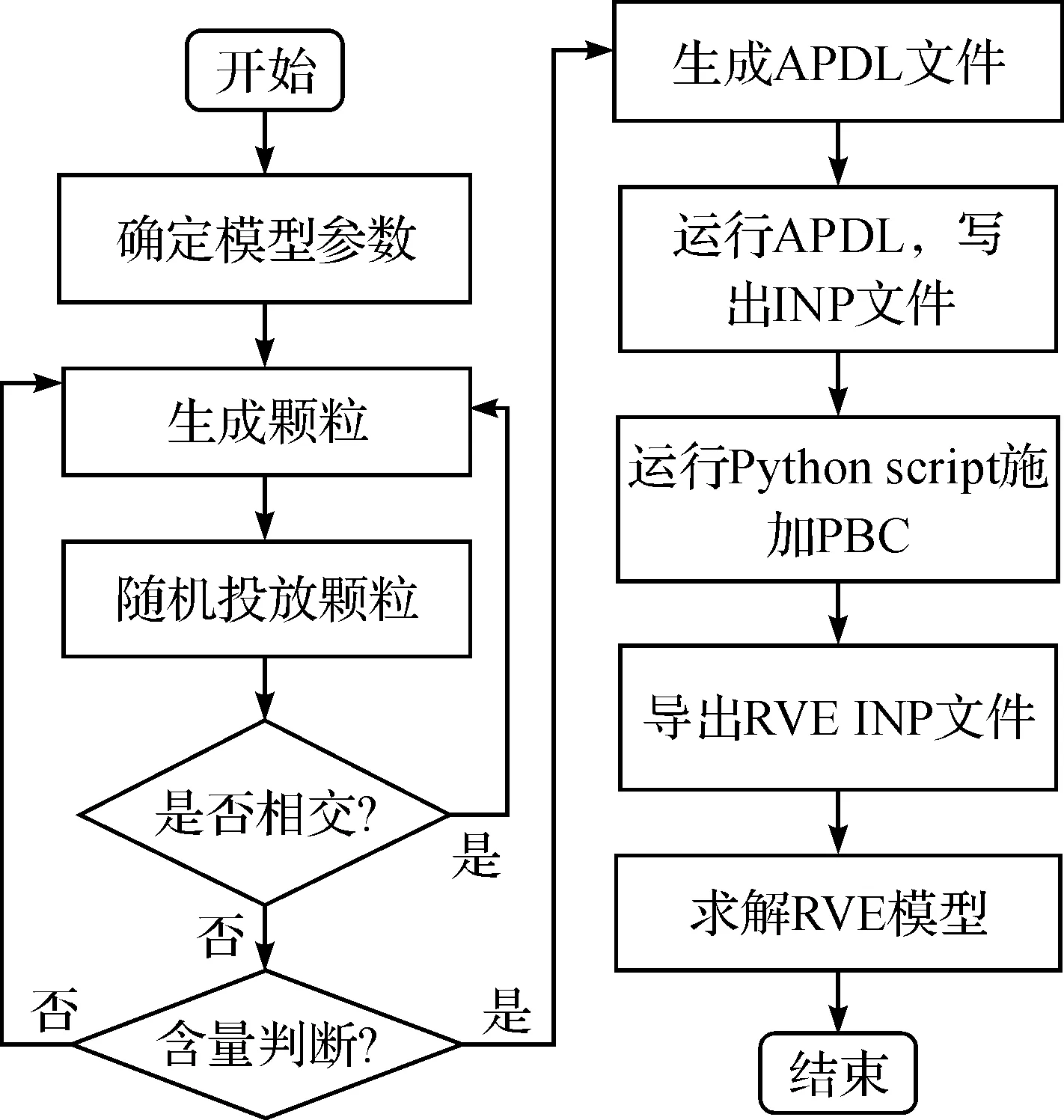
图1 RVE建模及分析流程图Fig.1 Flowchart of RVE modeling and its analysis

所构建分析的RVE的尺寸大小均为1×1 mm，单元类型均为平面应变单元，后续计算分析的加载方式均为单向拉伸.基体为环氧树脂，弹性模量为Em=3.5 GPa，泊松比μm=0.35，屈服强度σs=35 MPa，切线模量Gm=0.1 GPa.颗粒为二氧化硅，弹性模量Ef=80 GPa，泊松比μf=0.23.

图2 RVE有限元模型Fig.2 Finite element model of RVE

2 周期性边界条件

复合材料宏观上呈现出RVE重复叠加的周期性分布，对其进行均质化计算施加周期性边界条件更符合真实力学响应.RVE的边界上需要满足边界上没有分离也没有重叠的变形协调条件和相对边上的应力矢量的方向相反大小相同的应力连续条件.对RVE施加周期性位移边界条件，能够满足以上两个条件[11].

2.1 公式推导

对于具有周期性分布结构的复合材料，Suquet[12]给出了周期性位移场的表达式为

(1)

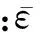
Xia等[13]给出了平行边界面的三维RVE模型周期性边界条件的一般性表达形式为

(2)

2.2 有限元实现

采用二维RVE模型，边界示意图，如图3所示，将其边界上的节点分为角节点和非角节点两类节点形式.

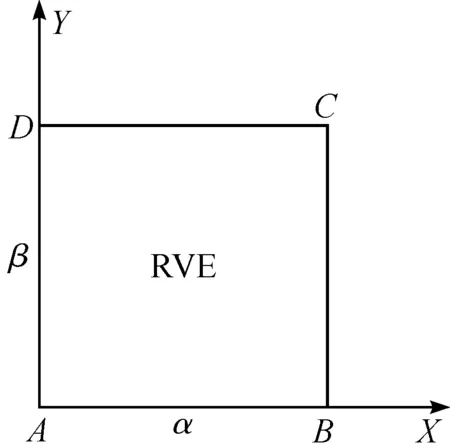
图3 RVE边界条件示意图Fig.3 Illustration of RVE boundary condition

在ABAQUS中，实现周期性边界条件需要将边界上节点的约束方程转换到内部的节点上.若边界上节点的约束方程组非独立，直接将约束方程施加到模型上会出现过约束问题，导致无法进行计算.为了避免过约束问题，需要消除约束方程组中非独立方程.根据相应的变形协调关系及式(2)，可消除非独立约束方程，得到两类节点约束方程组，即

(3)

(4)

式(3，4)通过Python script编程线性多点约束(MPC)的方式进行施加，线性多点约束方程的表达式为

(5)

其中：Cn为相关系数，需要指定数值；n为线性多点约束方程的项数.

值得注意的是式(3，4)右边RVE模型内的平均应变通过关联参考点，作为MPC方程的一项.施加线性多点约束方程的节点只能是节点集，包括参考点亦要建立节点集，边界上的每个节点建立独立集合是必要的.

3 均匀化求解

在RVE区域内，应用体积均匀化方法，其平均应力和平均应变计算公式分别为

(6)

其中：σij，εij分别为RVE的应力应变场变量；V为RVE的体积.

在ABAQUS中，Standard求解器求解非线性问题采用Newton-Raphson算法.基体弹塑性材料模型，在用户自定义子程序UMAT中，采用J2弹塑性流动理论实现.

在RVE求解过程中计算每个增量步的平均应力应变.首先通过用户自定义子程序UEXTERNALDB从外部文件中读取单元节点信息；然后通过用户自定义子程序URDFIL读取每个增量步的各个积分点上对应的应力应变值；最后在UEXTERNALDB中，将(6)分别展开为式(8，9)，计算平均应力和平均应变，并写到外部文件，其表达式为

(7)

(8)

4 计算分析

为了研究孔洞体积分数对颗粒增强复合材料的影响，探究颗粒和孔洞为单一因素时对基体的影响情况是必要的.故首先分析颗粒体积分数，颗粒材料，粒径对基体的影响.然后分析孔洞体积分数，孔径对基体的影响.最后分析孔洞体积分数对颗粒增强基体的影响.

4.1 颗粒体积分数、材料、粒径对基体的影响

图4为在不同的颗粒体积分数下考虑颗粒直径随机分布的等效应力—等效应变关系图.在此每种含量作5组颗粒随机分布的模拟分析.颗粒体积分数接近0%时，响应曲线与输入的基体材料曲线非常相近，这验证了均匀化计算编程的正确性.颗粒体积分数越高，对基体的增强作用越明显.在同一颗粒体积分数下，颗粒的随机分布对RVE响应曲线有一定影响，但影响不大.在同一等效应变下，颗粒体积分数越高，较前一颗粒体积分数等效应力的增量值就越大，这进一步表明：颗粒体积分数越大，增强作用越明显.

图4 考虑不同颗粒含量的RVE等效应力应变曲线Fig.4 The equivalent stress-strain curves of RVE with different particle fraction

图5为颗粒体积分数为20%时，12组模量比(基体材料参数不变，改变颗粒的弹性模量)的RVE响应曲线.当Ef大于Em时，颗粒对RVE有显著的增强作用；且随着Ef的增大，其对RVE的增强作用越明显.但Ef增加到足够大时，其增强作用将不明显.当Ef小于Em时，对RVE有软化作用；且随着Ef的减小，其软化作用越明显.但Ef减少到足够小时，其软化作用不再明显，此时可以把颗粒近似看作孔洞.从增强和软化范围角度分析，颗粒软化范围比增强范围大.因此，当制备颗粒软化复合材料时，颗粒材料弹性模量选取范围较颗粒增强时的大.

图5 考虑颗粒材料变化的RVE等效应力应变曲线Fig.5 The equivalent stress-strain curves of RVE with different particle material

图6为颗粒体积分数为20%时同一粒径(考虑两种情况：0.04 mm和0.1 mm)对RVE的影响.每种粒径下考虑5种随机分布.从图6中可知：颗粒越细小，表现出越好的力学性能.对于两种不同的粒径，它们在弹性阶段有着明显的界线；但是塑性阶段界线变得不太明显，相同粒径之间有微小波动，这说明颗粒的随机分布对于塑性阶段影响更大.

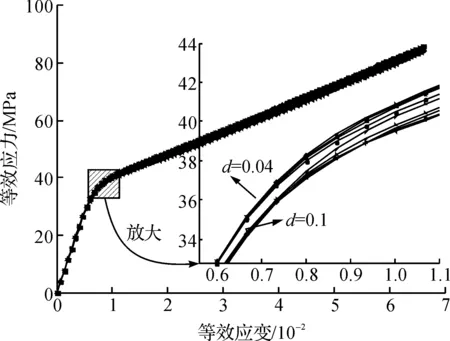
图6 在同一粒径下 RVE的等效应力应变曲线Fig.6 The equivalent stress-strain curves of RVE at the uniform particle diameter

4.2 孔洞体积分数，孔径对基体的影响

图7为考虑不同孔洞体积分数下RVE的响应曲线.孔洞体积分数小于5%时，每种体积分数只作了1组算例，而其余每一体积分数各作了5组算例.从图7中可知：体积分数越高，对基体的削弱作用越明显.当体积分数较小时，进入塑性阶段后，等效应力变化趋于平缓.当体积分数达到30%以上，进入到塑性阶段后，等效应力有一定斜率的增加.随着孔洞体积分数的增加，相同边界条件下，其等效应变数值越小，且对于30%和40%响应曲线，它们之间后段有部分交叉.此外，从图7中也可以观察到：当孔洞体积分数较小(小于5%)时，其等效应力已经大幅下降，也就意味着基体已被严重削弱.在同一孔洞体积分数下，相较颗粒增强材料，孔洞分布对RVE响应曲线有较大的影响.当体积分数增加时，影响略有减少，原因在于体积分数较大时孔洞分布相对均匀，分布的影响则减小.

图7 考虑不同孔洞体积分数的RVE等效应力应变曲线Fig.7 The equivalent stress-strain curves of RVE with different void fractions

图8为孔洞体积分数为20%时同一孔径(考虑两种情况：0.04 mm和0.1 mm)对RVE的影响.孔洞越细小，表现出越好的力学性能.两种孔径的响应曲线，弹性阶段界线不明显，塑性阶段界线开始变得非常明显，相同孔径下颗粒的响应曲线有较大波动，这说明孔洞的随机分布对于塑性阶段有着更大的影响.复合材料制备时应尽量减小大孔径的孔洞出现，以保证得到较好的力学性能.

图8 同一孔径下RVE的等效应力应变曲线Fig.8 The equivalent stress-strain curves of RVE at the uniform void diameter

4.3 孔洞体积分数对颗粒增强基体的影响

由于颗粒增强复合材料在制造过程中产生孔洞缺陷的含量不太大，所以在此分析了0.5%，1%，2%，5%孔洞体积分数对颗粒增强复合材料(考虑颗粒体积分数为20%)的影响.每种体积分数下分别考虑了两组算例，结果见图9.孔洞体积分数越大，对颗粒增强复合材料的削弱作用越加明显，且分布对颗粒增强复合材料的影响较大.当在孔洞体积分数为0.5%，1%，2%时，孔洞对基体的弱化作用非常明显，但是体积分数大于2%以后，其分布非常接近，即，随着孔洞再增大，其弱化作用趋于相近.这一结论与孔洞对纯基体的影响大致一致.在颗粒增强复合材料加工过程中，应尽量避免孔洞缺陷的产生.即便是小缺陷也会对材料的综合性能产生较大影响.

图9 孔洞体积分数对颗粒增强材料的影响Fig.9 The effect of void volume fraction on particle reinforced material

5 结 论

通过编程实现了含颗粒/孔洞的RVE模型构建，并对其施加了周期性边界条件.同时，基于ABAQUS二次开发实现了细观力学的均匀化方法在商业软件中的应用.计算分析了各个因素对颗粒增强复合材料的影响.结果表明：随着颗粒体积分数的增加，其对基体的增强作用越加明显，且颗粒越细性能也越好，但是颗粒体积分数的影响起到主导作用.此外，颗粒软化较颗粒增强对基体力学性能的影响范围大；随着孔洞体积分数的增加，其对基体的削弱作用越加明显，且孔径越大削弱作用也会增加，但是孔洞体积分数的影响起到主导作用；孔洞缺陷对颗粒增强复合材料的力学性能具有严重的削弱作用，即便是小缺陷也会对材料的综合性能产生较大影响.以上结论为颗粒增强复合材料的制备提供有意义的指导作用.

[1] ALVAREZ P,MENDIZABAL A,PETITE M M, et al. Finite element modelling of compressive mechanical behaviour of high and low density polymeric foams[J]. Mat-wiss. u. werkstofftech，2009,40(3):126-132.

[2] SMIT R J M, BREKELMANS W A M, MEIJER H E H. Prediction of the large-strain mechanical response of heterogeneous polymer systems：local and global deformation behaviour of a representative volume element of voided polycarbonate[J]. Journal of the mechanics and physics of solids,1999, 47(2):201-221.

[3] SEGURADO J, LLORCA J. Computational micromechanics of composites：the effect of particle spatial distribution[J]. Mechanics of materials,2006,38(8/9/10):873-883.

[4] 李伟,宋卫东,宁建国.考虑粒子分布特征的复合材料细观力学方法[J].固体力学学报,2010,31(4):339-345.

[5] 崔文凯,冯仰德,纪国良,等.随机颗粒复合材料模型生成与网格划分算法[J].数值计算与计算机应用, 2014,35(4):255-268.

[6] EL M A, KANIT T, IMAD A, et al. Effect of reinforcement shape on physical properties and representative volume element of particles-reinforced composites：statistical and numerical approaches[J]. Mechanics of materials，2015,83(4):1-16.

[7] SPAGGIARI A, O’DOWD N. The influence of void morphology and loading conditions on deformation and failure of porous polymers：a combined finite-element and analysis of variance study[J]. Computational materials science，2012,64(11):41-46.

[8] 王效贵,李晓叶.GTN损伤模型的算法研究及试验验证[J].浙江工业大学学报,2015,43(6)：660-665.

[9] 章巧芳,林文武,张钦,等.热驱动形状记忆聚合物三维力学本构模型[J].浙江工业大学学报,2015,43(1)：43-46.

[10] 彭卫兵,史贤豪,刘萌成,等.钢管混凝土叠合柱施工偏差对极限承载力的影响[J].浙江工业大学学报,2013,41(1)：80-83.

[11] XIA Z H, ZHOU C W, YONG Q L, et al. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites[J]. International journal of solids and structures,2006, 43(2)：266-278.

[12] SUQUET P. Elements of homogenization theory for inelastic solid mechanics[C]//SANCHEZ-PALENCIA E, ZAOUI A. Homogenization Techniques for Composite Media. Berlin：Springer-Verlag,1987:194-275

[13] XIA Z H, ZHANG Y F, ELLYIN F. A unified periodical boundary conditions for representative volume elements of composites and applications[J]. International journal of solids and structures,2003,40(8)：1907-1921.

(责任编辑：刘 岩)

Study on mechanical properties of particle reinforced composite materials containing voids

XU Yangjian, WU Pengwei, XU Lei, LIANG Lihua

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

The effects of particle volume fraction, particle diameter, particle material property and void etc. on particle reinforced composites were studied. A two-dimensional RVE model was built by programming, and the periodic displacement boundary conditions were given. Homogenization method was implemented by second development in the platform of ABAQUS, and the mechanical response of RVE was calculated and analyzed by using this method. The study shows that the influence range of softening particles on the mechanical properties of the matrix is larger than reinforcing particles, and its mechanical properties were greatly weakened by the void defects.

composite; homogenization; representative volume element; periodic boundary conditions

2016-01-11

国家自然科学基金资助项目(51375448,51375447)

许杨剑(1979—)，男，浙江东阳人，副教授，研究方向为固体力学，E-mail：xuyangjian571@163.com.

TB332

A

1006-4303(2016)05-0564-05