基于GPU的高效并行l1最小化算法

高家全,李泽界

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)



基于GPU的高效并行l1最小化算法

高家全,李泽界

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

多数l1最小化算法主要由稠密矩阵矢量乘(如Ax和ATx)和矢量运算组成.为使其适应大数据环境下的性能需求，基于GPU，利用其新的特征,提出了两个新颖的基于GPU的并行矩阵矢量乘.这两个算法实现了全局内存的合并访问，对任意给定矩阵，通过所使用的自适应分配线程数或warp数的策略，增加了鲁棒性.基于这两个算法，并以两个流行的l1最小化算法为例：快速迭代收缩阈值算法(FISTA)和增广拉格朗日乘子法(ALM)，提出了两个高效基于GPU的并行l1最小化算法.实验结果验证了提出的算法是高效的，并有良好的性能.

l1最小化；GPU；矩阵矢量乘；FISTA；ALM

l1最小化问题为min‖x‖1，须满足Ax=b，其中A∈(Rm×n(m≪n)是一个满秩的稠密矩阵，b(Rm是预先设定的矢量，x∈(Rn是未知解.l1最小化问题的解，也称为稀疏表达，已经广泛应用到多个领域，例如信号处理[1-2]，机器学习[3]和统计推理[4]等.为了解决l1最小化问题，研究者已开发出许多有效的算法.例如，梯度投影法[5]，截断牛顿内点法[6]，同伦法[7]，迭代收缩阈值法[8]，增广拉格朗日乘子法(ALM)[9]等.随着问题规模的增长，算法的执行效率很大程度上被消减.为提高其效率，一个有效的途径就是将这些算法移植到分布式或多核的架构上，例如目前流行的图形处理单元(GPU).自从NVIDIA公司在2007年[10]介绍了CUDA编程模型以来，基于GPU加速数据处理的研究已成为人们研究的热点[11-12].

大多数l1最小化算法，其运算主要由稠密的矩阵矢量乘和矢量操作组成.由于CUBLAS库[13]中已包含这些运算的高效实现，所以现有基于GPU加速的l1最小化算法[14]主要基于CUBLAS库.然而，在GTX980显卡上，对CUBLAS实现的矩阵矢量乘进行了测试，发现其会产生性能波动，随着行数或者列数的增长，且最大最小性能差距显著.因此，本研究基于GPU，针对Ax(GEMV)和ATx(GEMV-T)，分别提出一个自适应warp分配策略的GEMV核和thread分配策略的GEMV-T核.实验结果显示：该方法比CUBLAS更加鲁棒，而且总能保持高性能.基于GEMV核和GEMV-T核，以快速迭代收缩阈值算法FISTA和增广拉格朗日乘子法ALM为例，利用内核融合和新的GPU特性，例如洗牌指令(The shuffle instruction)和只读数据内存，提出了两个高效的基于GPU的并行l1最小化算法.该研究工作的主要贡献：1) 提出了两种新颖的基于GPU的并行稠密矩阵矢量乘算法；2)利用内核融合技术和新的GPU特性，并基于所提出的并行稠密矩阵矢量算法思想，实现了两个高效的并行l1最小化算法；3)通过实验，验证了方法的有效性.

1 两个l1最小化算法

1.1 快速迭代收缩阈值算法

l1最小化问题也被称为基追踪问题(The basis pursuit problem).在实际中，一个测量数据b经常含有噪声(例如测量误差ε)，这个被称为BPDN问题.它的一个变异被称为携带标量λ的无约束BPDN问题：

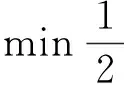
(1)

快速迭代收缩阈值算法[8](FISTA)是通过结合Nesterovs最优梯度算法实现的一个加速版本，拥有非渐进的收敛率O(k2).对于FISTA，它添加了一个新的序列{yk,k=1,2,…,n}，即

(2)

式中：soft(u,a)=sign(u)·max{|u|-a,0}为软阈值算子；y1=x0；t1=1；Lf为▽f(·)关联的李普希茨常数，可由计算ATA的特征谱得到(‖ATA‖2).

1.2 增广拉格朗日乘子法

增广拉格朗日乘子法[9](ALM)结合罚函数法和拉格朗日乘子法，对应增广拉格朗日函数为

Lρ(x*,λ)=‖x‖1+λT(Ax-b)+

(3)

式(3)可以通过迭代求解，即

(4)

式中{ρk}为单调递增的正序列.通过式(4)，可以同时求解最优解x*和λ*.式(4)的第一步称为x最小化，它是一个凸优化，可以通过FISTA求解.

2 CUDA架构

CUDA是一个通用的并行计算平台和编程模型.开发者可以使用CUDA C/C++定义函数(称为内核)，并通过CUDA线程并行执行这些内核.一个GPU拥有众多的计算核心，称为CUDA核心；这些核心被组织成一个可扩展的流多处理器(SM)的阵列.一个SM可以并行地执行成千上百个线程.当一个线程块被分配给一个SM，它又被划分为多个warp，每个warp拥有32个线程.最理想的情况，当这32个线程具有相同的执行路径时，指令执行效率最高.

GPU内存包括片上内存，如共享内存和L1缓存，和板载内存，如全局内存.全局内存容量最大，并被所有SM共享，然而由于全局内存位于片外的板载DRAM，其低带宽和高延迟经常导致存取访问慢.共享内存被同一个线程块内的所有线程共享，提供高带宽和低延迟，但容量小.L1缓存和只读数据缓存被同一个SM内的所有线程共享，且存取速度能与共享内存一样快.相比不可控的L1缓存，只读数据缓存是可控的，容易被利用.

3 GPU实现

3.1 鲁棒的矩阵矢量乘

本节提出两个矩阵矢量乘内核，包括Ax(GEMV)和ATx(GEMV-T)，其中A∈Rm×n.这里使用以0开始索引的按行存储方式来存储矩阵A，并利用填充策略优化全局内存访问性能，从而提高了访问效率.

3.1.1 GEMV核

Ax(GEMV)运算由m个内积组成(每个内积为A的一行和x相乘)，且每个内积是独立的.因此，在设计GEMV核时，可分配一个warp或者多个warp去计算一个内积.为优化GEMV核的性能，本研究提出如下的自适应warp分配策略，选取k个warp计算一个内积为

minw=sm×2 048/(k×32)m≤w

(5)

式中：sm为流多处理器的数目；m为矩阵的行数.GEMV内核伪代码描述为

输入:A,x,k,h,m,n;

输出:b;

1. __shared__xP[],bP[];

2. bVAL←0.0f;

3. lane←threadIdx.x&31; wid←threadIdx.x>>5;

4. wgSize←32×k; wgid←threadIdx.x/wgSize;

5. hub←threadIdx.x&(wgSize-1);

6. row←blockIdx.x×h+wgid;//行索引分配

7. for row tom-1 with row+=h×gridDim.x

//第一个阶段

8. bVAL←0; Aid←row×n+hub;

9. for xid=threadIdx.x ton-1 with xid+=blockDim.x

//x-load步

10.xP[threadIdx.x]←x[xid];

11. __syncthreads();

//partial-reduction步

12. fori=hub to blockDim.x-1 withi+=wgSize

13. bVAL←bVAL+A[Aid]×xP[i];

14.Aid←Aid+wgSize;

15.end

16.__syncthreads();

17.end

//warp-reduction步

18. 使用洗牌指令完成warp内的归约操作

19.iflane==0 bP[wid]←bVAL;

20.__syncthreads();

//第二个阶段

21.ifwid==0

22.bVAL←bP[lane];

23. 使用洗牌指令完成warp内的归约操作

24.iftid%k==0 b[row+threadIdx.x/k]←bVAL;

25.end

26.end

GEMV内核的主要步骤包括两个阶段，第一个阶段有三个步骤：x-load步,partial-reduction步和warp-reduction步.在x-load步中，一个线程块的所有线程并行地读取矢量x的每个元素到共享内存xP.因为x的尺寸很大，所以x被分块读进共享内存，大小为线程块尺寸.通过上述方式，保证了x的访问是合并的，并且通过共享x的片段，减少了访问次数.在partial-reduction步中，每次完成x片段的加载后，同一个warp组(k个warp组成一个warp组)内所有线程并行地执行x的部分归约操作(详见程序描述的12～15).显然，每个线程最多执行|n/wgSize|(n为矩阵A的列数，wgSize为warp组内线程数)次归约操作，并且对于访问全局内存上的矩阵A也是合并的.然后，使用洗牌指令实现warp-reduction步(warp内归约操作)，并将结果存在共享内存上.

在第二阶段，将warp-reduction步的结果归约为最终的输出.当k=1时，一个warp组只有一个warp.只需要第一个阶段，便可将结果输出(因为篇幅，核省略).同时，对于k=32的情况，由于不需要加载矢量x到共享内存，可直接将x加载到寄存器，所以需一个新核(因为篇幅，该核省略).

3.1.2 GEMV-T内核

ATx(GEMV-T)运算由n个内积组成(每个内积为A的一列和x相乘)，且每个内积是独立的.由于GEMV-T中的矢量x尺寸较小，所以在设计GEMV-T核时，可分配一个线程或者多个线程去计算一个内积.为优化GEMV-T核性能，本研究提出如下的自适应thread分配策略，选取k个线程计算一个内积为

mint=sm×2 048/kn≤t

(6)

式中：sm为流多处理器的数目；m为矩阵的行数.GEMV-T内核伪代码描述为

输入:A,x,k,h,m,n;

输出:b;

1.__shared__xP[], bP[];

2.bVAL;

3.wid←threadIdx.x>>5;lane←threadIdx.x&31;

4.wgSize←32×h;wgid←threadIdx.x/(wgSize);

5.col←blockIdx.x×32+32×wgid+lane; //列索引分配

6.forcolton-1withcol+=k×32×gridDim.x

//第一个阶段

7.bVAL←0;Aid←col+wid%h×n;

8.forxid=threadIdx.xtom-1withxid+=blockDim.x

// x-load步

9. xP[threadIdx.x]←x[xid];

10. __syncthreads();

11. //partial-reduction步

12. fori= wid%hto blockDim.x-1 withi+=h

13. bVAL←bVAL+A[Aid]×xP[i];

14. Aid←Aid+h×n;

15. end

16. __syncthreads();

17. end

18.bP[tid]←bVAL;

19. __syncthreads();

//第二个阶段

20. if wid%h==0

21. for bPid=tid to tid+32×h-1 with bPid+=32

22. bVAL←bVAL+bP[bPid];

23. end

24.b[col]←bVAL;

25. end

26. end

GEMV-T内核的主要过程也包括两个阶段，第一个阶段有两个步骤：x-load步和partial-reduction步.其中，x-load步跟GEMV内核执行一样的功能.在partial-reduction步中，由于使用以0开始索引的按行存储方法存储矩阵，因此如果线程组(k个线程组成一个线程组)的组织不合理，对于全局内存上的矩阵A的访问将是不合并的.

因此，为确保访问是合并的，线程组的创建根据如下：

定义1 假设线程块大小是s，h个线程一起被分配给ATx中的一个内积，而且z=s/h.那么，线程组组织如下：{0,z,…,(h-1)×z},{1,z+1,…,(h-1)×z+1},…,{z-1,2×z-1,…,2×(h-1)×z-1}.

对于已经完成加载的x片段，同一个线程组内所有线程并行地执行归约操作，与GEMV核相似.由于同一个线程组内线程经常不属于同一个warp，所以不能使用洗牌指令实现warp内归约操作.因此，在第二阶段，将partial-reduction步结果保存在共享内存上，然后再进行归约，并将归约结果输出.

3.2 并行的FISTA和ALM

在FISTA中，完成每次迭代需要6个操作，如图1所示.为了减少对应的内核数目，节约内核调用开销，避免双倍数据加载，这里对这些内核进行了融合.如图1所示，内核1融合了GEMV和矢量操作1；内核3融合了余下的矢量操作.进而，通过融合技术，核总数从6个降到3个.对于图1中的内核，基于GEMV核和GEMV-T核的思想，很容易实现内核1和内核2.CUBLAS虽然有着矢量运算的高效实现，但无法实现多核合并.因此，这里采用文献[15]的方法，通过多核融合，实现了内核3.

在ALM中，其x最小化可以通过FISTA求解，因此只需设计新的核函数实现dual update操作λk+1=λk+ρk(Axk+1-b).显而易见，基于GEMV核的思想，很容易并行实现这个dualupdate操作.这里分别称并行的FISTA和ALM为GFISTA和GALM.

图1 内核融合Fig.1 Kernel fusion

3.3 优 化

随着l1最小化算法的不断迭代，软阈值操作使得矢量x变得越来越稀疏.因此对于Ax，当输出向量x的第i个元素为0，那么A的第i行就不需要被访问了.利用这个稀疏性可减少对于全局内存上矩阵A的访问次数.

4 实 验

这一节测试所提出来的GEMV核、GEMV-T核、GFISTA和GALM的有效性.实验环境如下：一台IntelXeon双核CPU配一个NVIDIAGTX980显卡，使用CUDA7.5的编译运行环境.所有测试使用同一个测试矩阵集，如表1所示，这些矩阵按照正态分布随机生成.

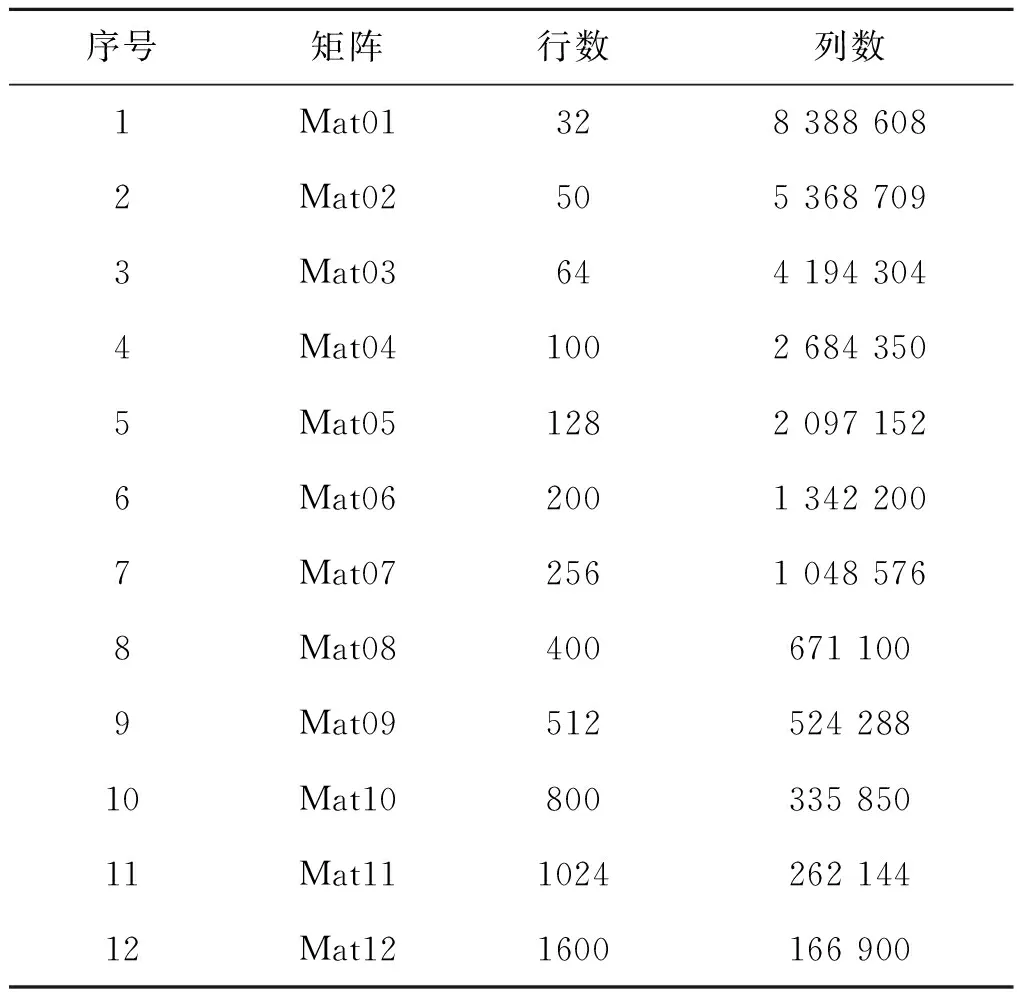
表1 测试矩阵

首先，使用上述测试矩阵与CUBLAS库进行比较，来验证所提出的GEMV核和GEMV-T核的有效性和鲁棒性.图2，3分别显示了两个并行稠密矩阵矢量乘内核与CUBLAS的性能比较.从图2可见：GEMV核相比CUBLAS，对于不同规模的矩阵，始终能够维持较高的性能，具有更佳的性能及稳定性.类似于GEMV核，GEMV-T核相比CUBLAS有着相似的结论.

图2 GEMV核与CUBLAS的性能比较Fig.2 Performance comparison of GEMV and CUBLAS

图3 GEMV-T核与CUBLAS的性能比较Fig.3 Performance comparison of GEMV-T and CUBLAS

其次，测试GFISTA和GALM的性能.为每一个测试用例，初始x0总是含有1 024个非零元素且b=Ax0.对于GFISTA，50次迭代后终止；对于GALM，10次外迭代后终止，并且每一次外迭代，内迭代都执行50次.表2列出了所有算法的执行时间，时间单位是秒.其中CFISTA和CALM分别是对应GFISTA和GALM在CPU上实现的串行FISTA和ALM算法.从表2可以看出：对所有用例，相比CFISTA，GFISTA能够获得范围从37.68到53.66倍的加速比，平均加速比是48.22.相比CALM，GALM获得的最大、最小和平均加速比分别为51.21，35.98，44.0.这些结果显示2个并行算法的性能提升是显著的.

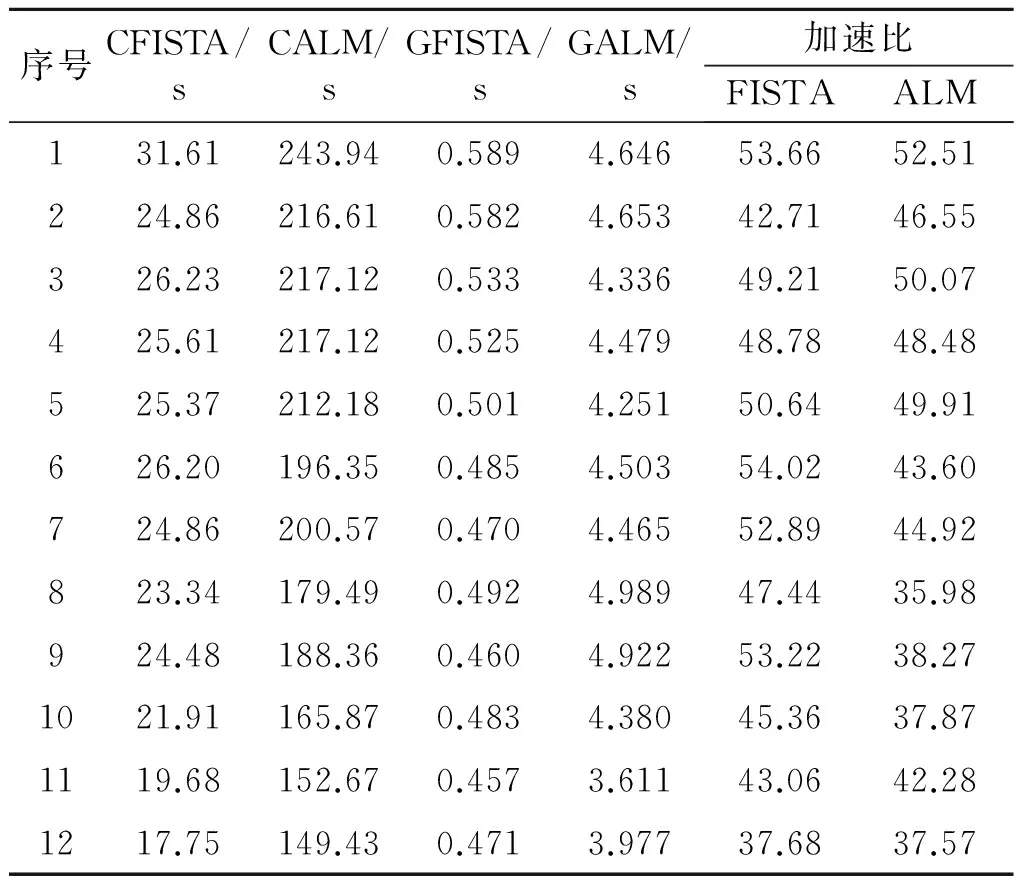
表2 GFISTA和GALM的性能

5 结 论

提出了两个新颖的GPU并行的矩阵矢量乘，进而基于这两个并行的矩阵矢量乘算法，利用内核融合技术和新的GPU特性，实现了两个高度并行的l1最小化算法(GFISTA和GALM)，并利用解的稀疏性进一步优化了性能.实验结果表明：提出的方法是有效的和鲁棒的，具有较高的并行性.

[1] DONOHO D L, ELAD M. On the stability of the basis pursuit in the presence of noise[J]. Signal processing,2006,86(3):511-532.

[2] TROPP J A. Just relax: convex programming methods for identifying sparse signals in noise[J]. IEEE transactions on information theory,2006,52(3):1030-1051.

[3] ELHAMIFAR E,VIDAL R. Sparse subspace clustering: algo-

rithm, theory, and applications[J]. IEEE transactions on software engineering,2013,35(11):2765-2781.

[4] WRIGHT J, MA Y, MAIRAL J, et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE,2010,98(6):1031-1044.

[5] FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE journal of selected topics in signal processing,2007,1(4):586-597.

[6] KIM S J, KOH K, LUSTIG M, et al. An interior-point method for large-scalel1-regularized least squares[J]. IEEE journal of selected topics in signal processing,2007,1(4):606-617.

[7] DONOHO D L, TSAIG Y. Fast solution of-norm minimization problems when the solution may be sparse[J]. IEEE transactions on information theory,2008,54(11):4789-4812.

[8] BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. Siam journal on imaging sciences,2009,2(1):183-202.

[9] YANG A Y, ZHOU Z H, Ganesh A, et al. Fastl1-minimization algorithms for robust face recognition[J]. IEEE transactions on image processing,2013,22(8):3234-3246.

[10] NVIDIA Corporation. CUDA C Programming guide[EB/OL].[2015-12-05].http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html.

[11] 范菁,吴佳敏.带显著性区域约束的高效视频全景拼接方法[J].浙江工业大学学报,2015,43(5):479-486.

[12] 丁维龙,陈淑娇,吴福理.一种基于物理特性的雨滴飞溅模拟算法[J].浙江工业大学学报,2014,42(5):586-590.

[13] NVIDIA Corporation. CUBLAS library[EB/OL].[2015-12-05]. http://docs.nvidia.com/cuda/cublas/index.html.

[14] NAGESH P, GOWDA R, LI B. Fast GPU implementation of large scale dictionary and sparse representation based vision problems[C]//Acoustics Speech and Signal Processing. Dallas: IEEE International Conference,2010:1570-1573.

[15] GAO J Q, LIANG R H, WANG J. Research on the conjugate gradient algorithm with a modified incomplete Cholesky preconditioner on GPU[J]. Journal of parallel and distributed computing,2014,74(2):2088-2098.

(责任编辑：陈石平)

Highly parallell1-minimization algorithms on GPU

GAO Jiaquan, LI Zejie

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

Thel1-minimization (l1-min) algorithms for solving thel1-min problem have been widely developed. For most ofl1-min algorithms, their components are the dense matrix-vector multiplications such as Ax and ATx, and vector operations. Utilizing the new features of the GPU, two novel matrix-vector multiplications are proposed. The two algorithms access the global memory in a fully coalesced manner, and enhance their robustness by designing a self-adaptive thread (warp) allocation strategy. Besides, based on the two algorithms, two highly parallell1-min algorithms (FISTA and ALM) are presented on the GPU. The experimental results show that the methods proposed are high efficent and have good performance.

l1-minimization; GPU; matrix-vector multiplication; FISTA; ALM

2015-12-17

国家自然科学基金资助项目(61379017)

高家全(1972—)，男，河南固始人，副教授，博士，研究方向为高性能计算、大数据分析与可视化、智能算法及应用，E-mail：gaojq@zjut.edu.cn.

TP338.6

A

1006-4303(2016)05-0495-06