沪深300股指期货对A股市场波动性实证研究

夏丽娜，洪历

沪深300股指期货对A股市场波动性实证研究

夏丽娜，洪历

文章对沪深300指数日收盘价日收益率建立ARMA模型，并使用GARCH模型和EGARCH模型分析引入股指期货对A股市场波动性的影响，发现引入股指期货减轻了A股的波动性及非对称型。

股指期货；A股市场波动性；GARCH模型；EGARCH模型

一、引言

股指期货是一种金融衍生工具，以股票价格指数为标的，买卖双方根据事先约定，在未来某一特定时间以约定价格进行股指期货交易的一种标准化协议。

一般而言，股指期货的推出会产生额外交易，同时吸引新资金入场交易。股指期货的套利交易及投资组合使得期货与现货之间的关系更为稳定。

2005年4月8号沪深300指数开始发布，2010年4月16号沪深300股指期货正式推出，我国股指期货市场迅速发展起来。沪深300股指期货的推出对沪深300指数波动性影响问题成为了研究人员和投资者普遍关注的问题。

文章通过研究2005年4月8号到2016年5月6号的沪深300指数的收盘数据，分析沪深300股指期货推出对股票现货市场波动性的影响，通过对沪深300指数日收益率数据建立ARMA模型并对该模型的残差在引入虚拟变量的情况下建立GARCH模型和EGARCH模型来分析股指期货的推出对现货市场波动性和杠杆效应的影响，并阐述了出现该现象的原因，这对于投资者制定投资策略以及政府机构出台金融政策稳定市场都具有很好的参考价值。

二、数据选取与统计描述

（一）数据选取

文章使用沪深300指数日收益率数据作实证分析。选取2005 年4月8号到2016年5月6号沪深300指数日收盘价（Ct）作为原始数据，数据来源为Wind数据库，共2693个数据。日收益率用指数收盘价的对数之差表示:Rt=lnCt-l-lnCt-1，故沪深300指数的日收益率数据共2692个。

（二）描述性统计

图1反映了日收益率序列的分布情况。右边为样本的描述统计量值。

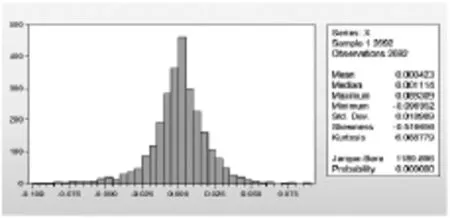
图1　沪深300指数日收益率序列分布图

表1　沪深300指数日收益率序列描述统计量

由表1可知，序列Rt的偏度S=-0.516560＜0，峰度K=6. 086518＞3，其与标准正态分布（S=0，K=3）相比，日收益率序列略微左偏并为尖峰厚尾形态。

（三）沪深300指数日收益率序列平稳性检验

文章运用的是ADF单位根检验方法。ADF值小于给定显著水平下的临界值时，表明该时间序列没有单位根，即该序列为平稳序列。反之，则为非平稳序列，需要对序列进行差分处理，以使序列平稳。

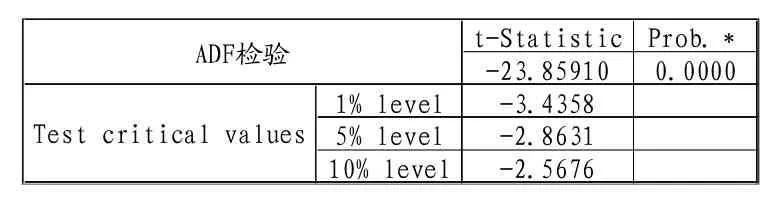
表2　ADF单位根检验结果

使用Eviews8.0软件对日收益率序列进行单位根检验。检验结果如表2所示，ADF=-23.85910，小于1%显著性水平下的临界值-3. 4358即样本时间序列不存在单位根，可见日收益率序列是平稳序列，可对其建立ARMA模型。

三、实证分析

（一）沪深300指数日收益率序列ARMA模型的建立

1.自回归移动平均方程的建立

使用AIC准则和SC准则对模型阶数进行选择，通过Eviews8.0软件对序列分别进行ARMA（1，1）、ARMA（1，2）、ARMA（2，1）、ARMA （2，2）回归分析，ARMA（2，2）模型由于不满足宽平稳的条件，不予考虑。表3中第一行的AIC值和SC值最小，所以选ARMA（1，1）较为合适。

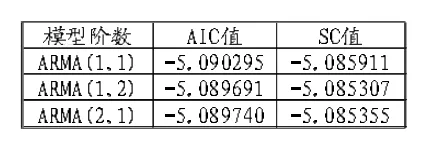
表3　不同阶数模型的AIC值和SC值

2.参数估计

使用Eviews8.0对沪深300指数收益率数据建立ARMA（1，1）模型，进行参数估计，结果如表4。所以得到的模型为：

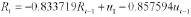
表4　ARMA（1，1）模型参数估计结果

3.ARCH效应检验

通过ARCH-LM检验来判断该模型残差序列是否存在条件异方差。再对其残差进行滞后8阶的ARCH-LM检验，结果如表5所示。

表5　ARMA（1，1）模型残差滞后8阶的ARCH效应检验

表5中LM统计量（Obs＊R-squared）的相伴概率为0，表明模型残差序列存在高阶ARCH效应，故选择对ARMA（1，1）模型残差建立GARCH模型。

（二）GARCH模型的选择与建立

对收益率序列ARMA模型的残差建立GARCH模型。通过AIC准则、SC准则来确定模型的阶数，结果如表6，应该选择GARCH（1，1）模型。

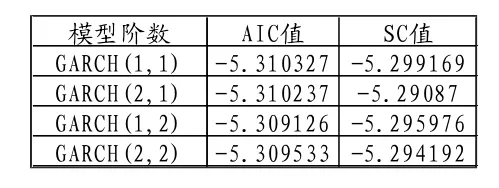
表6　不同阶数的GARCH的AIC值和SC值

对ARMA（1，1）模型残差建立GRACH（1，1）模型之后，对该GARCH（1，1）模型的残差进行卡方检验以检验其相关性，结果GARCH模型的残差序列相互独立，不存在相关性，说明GARCH模型已经成功提取了ARMA模型残差中的信息，使得GARCH模型的残差成为白噪声。再对GARCH模型的残差进行ARCH效应的LM检验，分别进行1阶和8阶检验，结果如下，说明GARCH模型的残差已经不存在ARCH效应。

表7　GARCH（1，1）残差1阶ARCH效应检验

表8　GARCH（1，1）残差8阶ARCH效应检验

为了检验引入指数期货对A股波动性的影响，文章引入了一个（0，1）的虚拟变量序列dt。股指期货推出前，该变量值为0；推出后该变量值为1。引入虚拟变量之后的GARCH模型形式为：

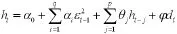
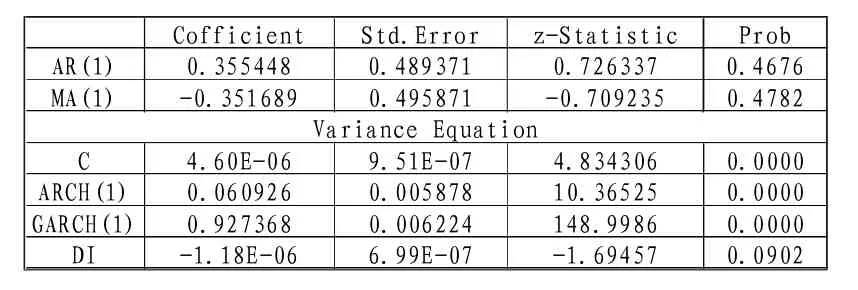
表8　GARCH（1，1）模型参数估计结果

对该GARCH模型的残差进行滞后8阶的ARCH-LM检验，检验结果如表9，LM统计量（Obs＊R-squared）值为0.671954，大于置信水平0.05，表明经过GARCH（1，1）处理后，残差序列已不存在ARCH效应。方差方程中的ARCH项和GARCH项的系数之和（αi+βi）为:0.060926+0.927368=0.988294，小于1，满足GARCH（1，1）模型宽平稳的参数约束条件。

表9　GARCH（1，1）模型残差8阶ARCH-LM检验

（三）EGARCH模型的建立

股票市场对利好和利空消息的反应一般不同，对收益率序列建立EGARCH（1，1）模型，以验证A股市场对利好、利空消息反应的非对称性。下面是引入虚拟变量后EARCH模型的形式：

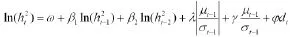
μt-1＞0表示“利好消息”，给指数带来λ+γ倍的冲击；μt-1＜0表示“利空消息”，给指数带来λ-γ倍的冲击。所以γ＜0时，A股市场存在杠杆效应。

分别对股指期货推出之前的数据和推出之后的所有数据建立EGACH（1，1）模型。再对所有数据在引入虚拟变量的条件下建立EGACH（1，1）模型。结果如表10所示，不论是股指期货推出之前还是之后，γ值都为负数，说明不论是推出股指期货之前还是之后，杠杆效应都是存在的。推出股指期货之后整体数据的杠杆效应比推出股指期货之前更小且引入虚拟变量时更加明显。这表明引入股指期货减轻了A股的波动，削弱了市场风险。可能是由于引入股指期货改变了我国证券市场长期单向的交易制度，使得投资者可以进行双向操作，一定程度减轻了市场波动性。

表10　股指期货推出前后对比表

四、结论

（一）沪深300指数日收益率序列是平稳时间序列，可以建立ARMA模型。通过ARCH-LM检验发现该模型的残差存在高阶条件异方差，并引入GARCH模型，很好的解决了残差条件异方差问题，使得GARCH模型的残差为白噪声。

（二）文章通过GARCH（1，1）、EARCH（1，1）模型就引入股指期货事件对A股市场的波动性进行了实证分析，发现引入股指期货一定程度上减轻了A股市场的波动性，削弱了投机氛围。

（三）A股市场在引入股指期货前后都存在杠杆效应，且推出股指期货后，利好消息、利空消息的影响都降低了。

［1］Antoniou，PhiHolmes.Futures Trading，Information and SpotPrice Volatility:Evidence for the FTSE-100 Stock Index Futures Contract GARCH［J］.JournalofBankingandFinance，1995，vol.19（1）:117-129.

［2］谷耀，陆丽娜.沪深港股市信息溢出效应与动态相关性——基于DCC－（BV）EGARCH－VAR的检验［J］.数量经济技术经济研究，2006，（08）:23－27.

［3］郭彦峰，黄登仕，魏宇等.我国指数期货与现货之间的价格发现和波动性外溢［J］.管理评论，2009，21（8）:13-22.

［4］谢磊，王业成.股指期货对股票现货市场波动性影响的实证研究［J］.技术经济，2010，（03）:73-78.

［5］张孝岩，沈中华.股指期货推出对中国股票市场波动性的影响研究——基于沪深300股指期货高频数据的实证分析 ［J］.投资研究，2011，10（30）:112-122.

［6］周璐.股指期货、股市波动性与价格引导——基于沪深300数据的研究［J］.理论探讨，2013，（24）:117-119.

［7］王起凡.沪深300股指期货对我国股市波动性影响的研究［J］.现代商业，2015，（21）:182-185.

［8］李继祥.VaR及对证券投资基金的VaR测算［J］.西部财经论坛，2003，（02）:60-64.

夏丽娜，女，江苏泰州人，上海海事大学研究生，研究方向：海运、物流经济与金融；

洪历，上海海事大学经济管理学院。

F830

A

1008-4428（2016）08-101-03