基于QPSO算法的冷链物流配送运输问题的研究

高晓巍

基于QPSO算法的冷链物流配送运输问题的研究

高晓巍

随着中国消费者生活模式的转变，冷链产品的销售比重迅速加大，优化冷链物流运输路径成为提高企业竞争力的关键。文章以物流运输成本最小化与顾客满意程度最大化为目标，利用QPSO算法进行求解。仿真实验结果表明，QPSO算法在求解多配置中心多车辆的冷链物流运输路径问题中呈现出了较好的稳定性与收敛速度。

量子行为粒子群算法；冷链物流；客户满意度

一、引言

随着现代化制冷技术的发展，海、陆、空运输网络的建立，人们对生鲜冷冻食品的品质和安全提出了更高的要求，这为冷链物流的发展提供了有力的契机。冷链物流是指以保证易腐食品品质为目的，以保持低温环境为核心，以现代化制冷技术为手段的物流信息管理和配送系统。然而我国冷链物流的发展起步较晚，在物流设施、冷藏技术设备及配送管理等方面与欧、美、日发达国家差距较大。据不完全统计，我国每年由于冷链物流问题所带来的经济损失高达100亿美元。因此，优化配送运输路径成为降低社会经济损失，提高企业经济效益的有效途径之一。

二、文献综述

物流配送运输路径优化方法主要包括精确算法和群体智能算法两种。由于群体智能算法的并行性、分布式、易操作性等特点使得遗传算法、粒子群、蚁群等典型的群体智能算法在冷链物流研究中得到广泛的应用。刘镇等人在考虑多源实时交通信息的基础上建立了运输成本和配送时间的优化模型，并在云计算环境下利用粗粒度并行遗传算法对模型假设进行了有效性的验证；陶荣综合考虑配送、货损与惩罚三个主要成本要素建立了带有时间窗的优化配送运输模型，并通过蚁群算法验证了模型的有效性和可行性。他所提出的多温共配思想为冷链物流的发展注入了新鲜血液；量子粒子群（QPSO）优化算法是在粒子群（PSO）优化算法的基础上，从量子力学的角度提出的一种新型算法。QPSO算法通过建立δ势阱模型使处于量子束缚态的粒子按照一定的概率密度实现全局收敛，已经证实QPSO算法克服了PSO算法因速度限制搜索空间受限的问题。本文采用量子粒子群优化算法实现模型假设的验证。

三、冷链产品物流配送路径优化模型

冷链产品物流配送路径优化问题可描述为在一定范围内和约束条件下，将冷链产品通过储运的方式实现在多个配送中心与供给客户之间的空间位移，并使目标函数达到最优化。

假设冷链产品的配送中心有M个，运输车辆有P辆（载重量均为r），客户有N个（货物需求为ni其中i=1，2，…，N），且每辆运输车完成任务后均返回配送中心。客户与配送中心的编码分别为1，2，…，N，N+1，N+2，...，N+M；变量定义如下：

其中客户在［Bi，Li］内的意度为1，在该区间以外客户的满意度随时间ti而线性减少，α，β是客户对时间的敏感系数。

冷链产品的储运直接影响产品的质量与安全，因此，需同时考虑物流运输路径最短和客户满意程度两个最优化问题，构建数学建模如下：

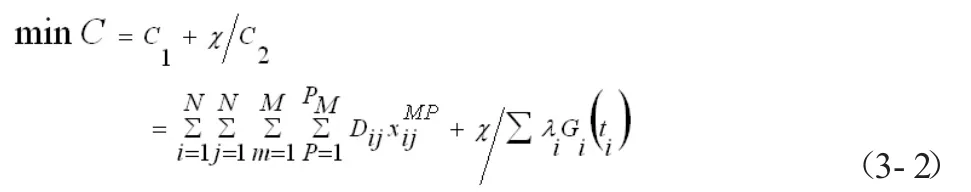
其中Dij表示两个客户i，j之间的距离；配送中心M具有PM辆储运货车。

目标函数需满足如下约束条件：

（1）参与储运的车辆不能超出配送中心的总车辆数，即

（2）参与储运的车辆的承载数量是有限的，约束如下：

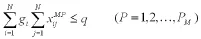
（3）每个客户配送服务仅一次

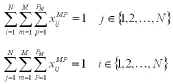
（4）配送路径无子回路

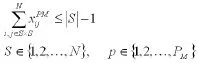
在目标函数中引入罚函数以约束车辆容量，

其中ξ取值足够大时不可行解在迭代过程中将被淘汰。

四、基于QPSO算法的物流运输路径优化问题

（一）QPSO算法

QPSO算法从量子力学理论出发，通过建立δ势阱模型束缚粒子，在收索空间中受量子束缚的粒子以一定的概率密度分布，当粒子与中心的距离趋于无穷大时，其概率密度趋于零。

在一个M维的目标搜索空间中，由N个粒子组成的种群的决策变量为粒子第t次迭代的位置向量，粒子个体最好位置为以最小优化问题minf（x）为例，由下式确定：

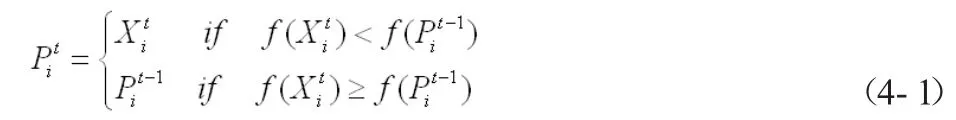
粒子的演化方程

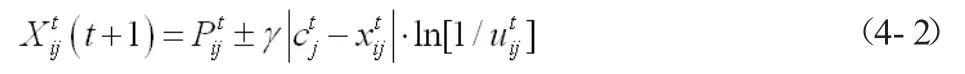
当参数γ由1.0线性递减到0.5时效果较好。

（二）粒子编码

构造X1与X2两个N维子向量。X1为车辆信息，X1∈［1，p］，X2为车辆储运路径信息。假设2个配送中心，对12个客户进行储运服务，每个配送中心所拥有的车辆数分别为2，3，且这5辆车的编码分别为1至6。

表1　粒子编码

储运路线为：

配送中心1

车辆1的储运路径为：4→7

车辆2的储运路径为：10→11→8

配送中心2

车辆3的储运路径为：1→3

车辆4的储运路径为：12→9

车辆5的储运路径为：2→3→6

（三）基于QPSO算法的物流运输路径规划算法

QPSO算法流程如下：

第一步：取种群规模为N，最大迭代次数T，对粒子进行编码；

第三步：利用公式（4-3）计算平均最好位置；

第七步：转第三步继续迭代，达到迭代次T结束；

（四）仿真实验结果与分析

假设某地由3个配送中心对该地区的15个门店提供储运服务，每个配送中心1，2，3的车辆数分别为2，2，2，6辆车的编码分别为1，2，……，6；14个客户及3个配送中心在XOY平面的位置信息如下表2，表3所示

表2　客户信息

表3　配送中心信息

通过Matlab7.0对QPSO算法进行计算机仿真实验。结果表明了QPSO算法的可行性和有效性。储运路线如图1所示。

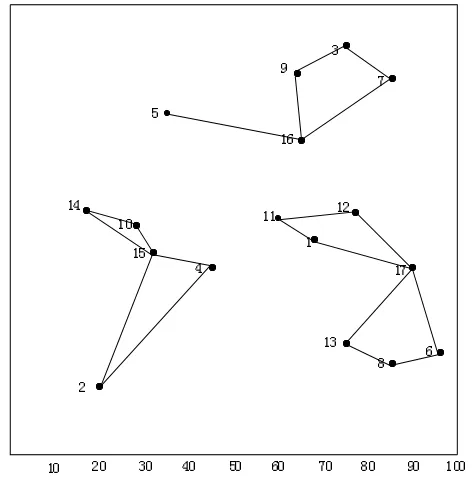
图1　最优配送方案图

经粒子解码得到有效路径为：

配送中心1的车辆1：15→10→14→15

配送中心1的车辆2：15→4→2→15

配送中心2的车辆3：16→5→16

配送中心2的车辆4：16→9→3→7→16

配送中心3的车辆5：17→12→11→1→17

配送中心3的车辆6：17→13→8→6→17

仿真实验结果如下：

表4　仿真实验结果

由上表可见QPSO算法在解决冷链产品物流储运路径问题中呈现出较强的稳定性与收敛性。

五、结束语

随着中国消费者对冷链产品需求量的增加及对产品质量安全性的重视，为冷链物流的发展提供了机遇，研究冷链产品的储运优化路径，是提高物流企业竞争力及消费者满意度的关键。本文从现代物流管理理念出发，以冷链产品的储运成本最小化与顾客的满意程度最大化作为优化目标，使得算法的研究与实现更具有现实意义。

［1］方凯，钟涨宝，王厚俊.贺岚基于绿色供应链的我国冷链物流企业效率分析［J］.农业技术经济，2014，（03）：50-53.

［2］邵瑞银.河南省农产品冷链物流现状、问题与对策［J］.企业经济，2013，（02）：15-17.

［3］刘镇，徐优香，王译.基于云计算的冷链物流配送车辆路径优化方法研究［J］.电子设计工程，2013，（04）：23-27.

［4］陶荣.基于蚁群算法的多温共配冷链物流配送问题研究［J］.物流技术，2014，（02）：31-34.

［5］孙俊.量子行为粒子群优化 ［M］.北京：清华大学出版社，2011，8.

［6］张仁堂，董海洲，乔旭光等.现代果蔬物流中冷链技术集成创新研究［J］.世界农业，2007，9（3）:47—49.

高晓巍，女，黑龙江齐齐哈尔人，齐齐哈尔大学理学院副教授，研究方向：智能规划、优化算法。

N945.12

A

1008-4428（2016）10-12-03