“小数乘整数”的教学设计与评析
2016-11-17江苏省扬州育才实验学校
江苏省扬州育才实验学校 徐 莹
“小数乘整数”的教学设计与评析
江苏省扬州育才实验学校徐莹
研究模式:小学数学计算新授课差异教学模式。
教学内容:苏教版五年级九册“小数乘整数”P68-69页。
理解:理解小数乘整数的竖式计算方法。
简单运用:会正确用竖式进行小数乘整数的计算。
复杂运用:应用计算解决一些简单实际的问题。
过程与方法:经历探索并理解小数乘整数的计算方法的过程,体验抽象概括及合理推理的学习方法。
情感、态度与价值观:使学生在探索计算方法的过程中,进一步体会知识之间的内在联系,培养初步的抽象、概括以及合理推理的能力,感受数学活动的乐趣。
教学重点:小数乘整数的笔算方法。
教学难点:积的小数点的位置。
教学准备:课件,作业纸。
课堂教学实录与评析:
一、预学查异
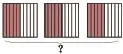
1.师:每个正方形后面都藏着一样的物体,掀开正方形看一看,你能用算式表示吗?
出示第1幅图,
生:5×3=15。
师:算式表示什么意思?
生:3个5相加。
师:几个相同的数相加,可以用乘法来表示。
2.师:图形后面藏的内容可多了,再来看一看,算一算。

出示第2幅图。
生:50×3=150。
师:怎么计算的?
生:5×3=15,所以50×3=150。
师:5表示什么?5×3得到15个什么?
【评析:本节课以两幅图让学生用乘法算式表示,说说算式表示什么意思并算一算作为预学,实际上就是对之前知识的复习与巩固。乘法的意义在二年级的时候学生就学过了,但是记忆有些零散。老师出示第一幅图时,有部分学生不知道如何去理解或不知道怎样去表述更加完整,需要学有余力的学生回答。之后有第一幅图作为铺设,第二幅图的表述就激起了学生的兴趣,很多学生都会表述,而且表述得很完整。这就是利用学生之间资源共享,让优等生去带动暂时后进生,一方面能促进学生对旧知的重拾,另一方面也调动了后进生的积极性。当然这样的两幅图也起到承上启下的作用,利用学生的已有经验,在学习新知时学生会利用知识之间的迁移,很好地将整数问题过渡到小数问题的研究。】

二、初学适异
1.出示第3幅图。
生:0.5×3。
师:算式表示什么意思?
生:3个0.5相加。
师:几个相同小数相加也可以用乘法表示。
算式怎么计算?
生:5×3=15,所以0.5×3=1.5。
师:5表示什么?5个0.1乘3得到什么?是多少?
2.出示第4幅图。
生:0.05×3
师:算式表示什么意思?怎么算?
生:5×3=15,所以0.05×3=0.15。
师:这里的5表示什么?15表示什么?
3.出示例题。
师:买3千克西瓜要多少元?你会算吗?

生:0.8×3。
师:怎么计算?
生:8×3=24,所以0.8×3=2.4。
4.师:比较0.5×3,0.05×3,0.8×3这三道算式,和以前学过的乘法有什么不一样的地方?
生:以前是整数乘整数,现在是小数乘整数。
揭题:今天学习小数乘整数
师:虽然是新知识,但我们在计算时,是把它转化成整数乘整数来计算的。
【评析:仍然利用两幅图,首先让学生根据两幅图说出乘法算式,很自然地将整数知识过渡到小数知识。然后根据图让学生表述0.5×3的算理,这里的根据图形让学生说算理,其实就关注到学生之间的差异。好的学生会直接根据0.5×3这道算式说算理,对于学习有些困难的学生就需要图的帮扶,在图形的帮扶下他们会很快地理解0.5×3为什么等于1.5,初步去感知为什么,也让学生理解算0.5×3实际是算5×3,为接下来的竖式计算埋下伏笔。当然在无形当中也渗透了数形结合的转化思想。学生对于小数乘整数算理的复述会联想或模仿整数问题去思考,利用图将算理不是流于表面,而是将算理融入到每位学生脑海里,真正理解及时消化。】
三、研学导异
1.竖式0.8×3。
师:小数乘整数,还可以用竖式来计算,谁愿意来试一试?
生板演,讲解竖式。
师:列竖式时,3为什么和8对齐?
生:计算时,是把0.8看作8来计算的。
师:和整数乘法一样,列竖式时,要保证两个乘数末尾对齐。
师:先算什么?
生:8×3=24。
师:24表示什么?
生:24个0.1。
师:积应是多少?
生:2.4。
师:小数点点在哪?
生:2和4中间。
师:在24上从右往左数一位,点上小数点。
师:回顾0.8×3的计算过程,先算什么?
生:8×3。
师:也就是把它转化成整数乘整数,再给它点上小数点。
【评析:小数乘法竖式的写法,与小数加减法不同,通常是写成末尾对齐。但老师没有直接告知而是让学生尝试用竖式计算。让学生陈述想法,这样由告诉改为思考,学生对末位对齐的书写不再停留于形式的记忆,而是在尝试、思考的过程中获得理解。其意图不仅仅是解决竖式书写的问题,更重要的是以此为切入口,让学生领悟、体会并明晰小数乘法转化成整数乘法的策略。】
2.尝试0.5×3,0.05×3。
①师:这两题你能用竖式计算吗?
生独立完成,展台展示,讲解。
第一题:
师:怎么计算的?
生:3×5=15,在1后面点上小数点。
第二题:
师:怎么计算?
生:3×5=15。
师:积的小数点从右数几位点上?
生:数两位。
师:前面整数部分没有怎么办?
生:在前面补0。
②比较
师:都是先算5×3,为什么一个积是1.5,另一个是0.15?
生:第一题表示15个0.1,第二题表示15个0.01。
师:为什么一个是15个0.1,而另一个是15个0.01?
生:乘数一个表示5个0.1,另一个表示5个0.01。
揭示:看来积的小数位数和乘数小数位数有着密切联系,有什么联系呢?同桌相互讨论。
指名回答。
生:乘数是几位小数,积就是几位小数。
③想一想
师:根据148×23=3404这一题,你能写出下面四道算式的得数吗?
14.8×23=148×2.3=148×0.23=1.48×23=
生独立完成,指名回答,并说说想法。
④师:结合前面的计算,你知道小数乘整数怎么计算吗?
引导小结:把它看作整数乘整数来计算,乘数是几位小数,积就是几位小数。
【评析:本节课的另一个重点就是讨论积的小数位数,正确点小数点的问题。让学生尝试算0.5×3,0.05×3并比较,通过学生之间的讨论去发现:积的小数位数和乘数小数位数有着密切联系。以同桌讨论做铺垫,在交流的过程中,老师扮演学习活动的组织者,将研究学习的平台交给学生自己,让学生去探讨、去发现、去交流。利用了生与生之间的沟通、师与生之间的对话,让学生带动学生,真正体现了共同认识、共同进步,从而达成预期的教学目标。】
3.试一试。
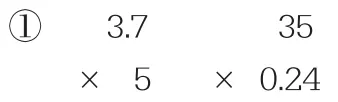
生独立完成。反馈,说说怎么计算的。
②0.68×9=1.05×24=
师:这两题你会用竖式计算吗?
独立完成。反馈,说说计算过程。
4.解决实际问题。
做一套衣服要用布2.4米,做48套这样的衣服要用布多少米?
生独立完成,集体核对。
5.完成课堂作业
四、拓学展异
根据148×23=3404,写出下面一道算式:
()×()=3.404
生独立思考,指名回答。
生:0.148×2314.8×0.231.48×2.3……
师:像这样的算式还有很多,以后的知识会学到。
【评析:在课堂的尾声老师并没有“就此搁笔”,而是一道思考题掀起了学生思维的涟漪,让学生探究的步伐继续前行。由于这样题目答案的多样化,因此在学生不断地补充、不断地完善中解答,既是对本节课重点难点的回顾,又是对学生思维的训练,提高解决问题的能力。学有余力的学生先回答带动暂时后进生,让数学学习面向全体学生,人人都能获得良好的数学教育,不同的人在数学上得到不同的发展。】
