三维多物质欧拉界面处理的并行算法研究

龙文佳,李跃新

(湖北大学 计算机与信息工程系，武汉 430000)



三维多物质欧拉界面处理的并行算法研究

龙文佳,李跃新

(湖北大学 计算机与信息工程系，武汉 430000)

针对现有的算法无法对爆炸冲击进行有效的研究这一问题，在改进了Youngs界面技术的基础上设计了三维多物质Euler界面处理的并行算法;然后采用MPI标准进行了算法的程序设计并对程序进行了并行性能测试和不同分区的算例测试，测试结果表明并行算法对加速比有较大的提高，而不同分区对并行算法的计算结果并没有影响;最后应用所编写的程序对空中爆炸和聚能射流进行了仿真，结果表明程序的模拟结果与前人的研究数据是符合的，说明了程序的有效性。

爆炸与冲击;数值模拟;欧拉方法;并行计算;Youngs界面技术

0 引言

爆炸冲击涉及大量的非线性瞬态动力学问题，属于复杂大变形的流体弹塑性力学范畴，而Euler算法[1-2]对于解决该类问题具有很大的优势，但其很难描述各介质的界面，所以界面处理的精度问题一直是Euler算法的核心问题。Youngs界面技术能够对两种物质界面进行精确的处理，但在爆炸过程中，会涉及到多种物质的混合，只有各物质界面能实现网格类型的精确区分，才能得到正确的计算结果，故需对现有的Youngs界面技术进行改进以解决其无法对两种以上物质混合进行界面处理的问题。

针对上述问题，本文通过使用网格中量最大的物质来代替量最少的物质对Youngs界面技术进行改进，使其能够处理多物质混合界面，然后将其与Euler算法结合用来处理爆炸冲击问题。最后对改进的算法进行了并行设计及程序编写，并对空中爆炸和聚能射流进行了数值模拟，证明了算法及程序的正确性。

1 改进的多物质欧拉界面处理算法概述

在笛卡尔坐标系下，Euler方法对控制方程组采用算子分裂算进行离散。一方面，按物理效应分裂为Lagrange步和Euler步，Lagrange步计算偏应力、压力对内能和速度的影响，Euler步计算各网格之间质量、体积、动量和能量输运。另一方面，通过交替输运方法将多维输运问题转化为多个一维问题，同时能保证按网格间物质流通的方向完成输运。

在Euler算法中，当混合网格中有3种物质的时候，无法直接使用Youngs界面技术进行界面处理。为了使计算继续进行，将Youngs界面技术进行如下改进：首先按物质的体积份额进行从大打小排序，用最大的物质替代最少的物质，如此就将3种物质就转化为两种物质了，从而就可以继续应用Youngs界面技术进行界面处理。

2 算法的并行化及实现

2.1 Euler方法的并行计算理论分析

在Euler方法数值模拟的过程中，网格固定，物质在网格间流进流出。各网格的物质输运会导致其周围网格部分物理量的变化，而在输运算法中隐含的子区域间的关联性和数据相关性不容易被发现，而这两个问题仅存在于Euler的输运步中，是Euler方法并行计算[3-6]实现的关键。

2.1.1 数据子区域的划分和特点

并行计算需要将计算域划分为若干块来独立进行计算，那么各子区域间必然会存在重叠和相关的部分，具体如图1所示。

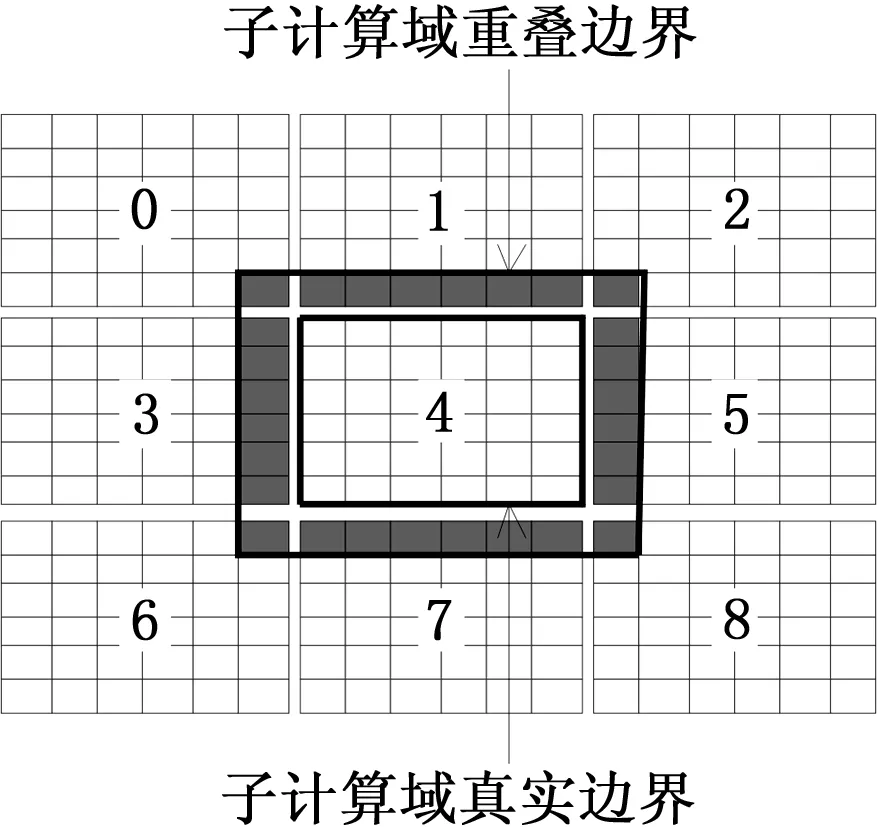
图1 重叠子区域

网格物理量的改变量等于该网格3个方向上的流进量减去流出量的差值，故Euler方法的输运歩里各网格的更新应包含该网格与邻近网格的输运。

以图2中的单方向输运为例，流场速度为正，则单方向k网格一次物理量的改变包含k-1和k网格的输运，其值为k-1网格流进量减去k网格流出量的差值。

图2 单向输运

因此对于图1中的区域4而言，需在其下边和左边分别增加一层网格，具体如图3所示。

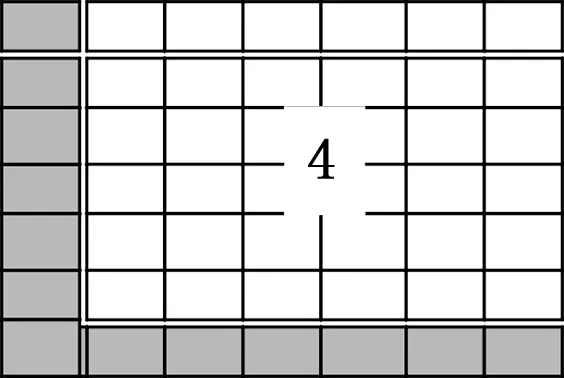
图3 输运相关性

此外，在实际运算中，k网格物理量的数值更新也需要知道k，k+1网格物理量的值，因此4号区域的右边和上边也要增加一层网格，但所增加的网络为虚拟网格，无需参与数据更新。在实际的并行算法设计中，要尽量避免在虚拟网格上进行通信，以免出错。

2.1.2 数据更新与通信的分析

由图2的分析可知，单方向输运的时候，网格物理量的输运变化会导致自身网格和其下阶段网格的物理量产生变化，但在实际计算中，由于CFL条件的限制，各网格的输运变化只会对其周围26个网格的物理量产生更新和影响，即网格输运的数据相关性。

可以使用原本未被更新的物理量来消除网格输运的数据相关性，但这样又会出现过量输运的问题。故综合考虑，将3个方向的输运转变为三重循环下的单一方向的输运，这是本文进行并行算法设计的基础。

2.1.3 变量数据的定义

并行计算设计中，涉及大量变量的定义和MPI库函数的调用。在变量的定义过程中，需注意各进程内私有变量的数据更新无法对其它进程中该变量的数据进行同步更新，这样就会出现错误，所以当私有变量的数据更新会对周围网格产生影响的时候，必须要将更新后的变量数据向相关进程进行传递。全局变量的数据一经改变，所有进程中该变量的数据都可以得到相应的更新。

2.2 并行前处理

2.2.1 创建可以任意划分的计算域

设计的并行程序能够完成计算域3个方向任意维度的划分，划分原则如下：

①计算域最外层的循环划分为较多的子域，内层循环尽量少划分子域；

②尽量将计算域划分为正方体，以使通信面积最小；

③在划分过程中，若3个方向的网格划分数目不同，则使外层网格最多。

设npx，npy，npz为X，Y，Z3个方向的分区数量(都为正整数)，那么计算域子区域的数目np=npx×npy×npz，子区域的编号myid可通过MPI库函数中的MPI_Comm_rank来获取，计算机的进程数目可通过MPI_Comm_size来获取,具体实现代码分别为：

MPI _Comm_ rank(MPI _Comm_world,myid, ierr)

MPI_Comm_size(MPI_omm_world,numprocs, ierr)

Mepx，Mepy，Mepz表示3个方向的进程坐标，具体如式(1)所示：

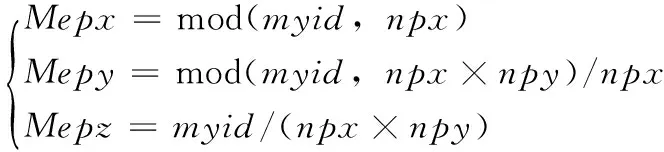
(1)

对于距计算边界较近的子区域，若其周围没有其它子区域，可使用MPI 的虚拟化子区域MPI_Proc_null。

用来确定与目标子区域相邻子区域的编号的公式如式(2)所示：

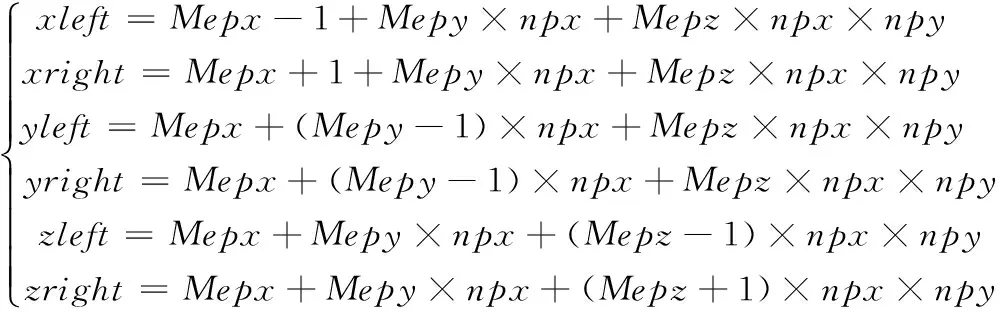
(2)

假设取X，Y，Z3个方向的分区数量分别为 2、3、2，那么共有12个子区域，其中一种划分方法如图4所示。

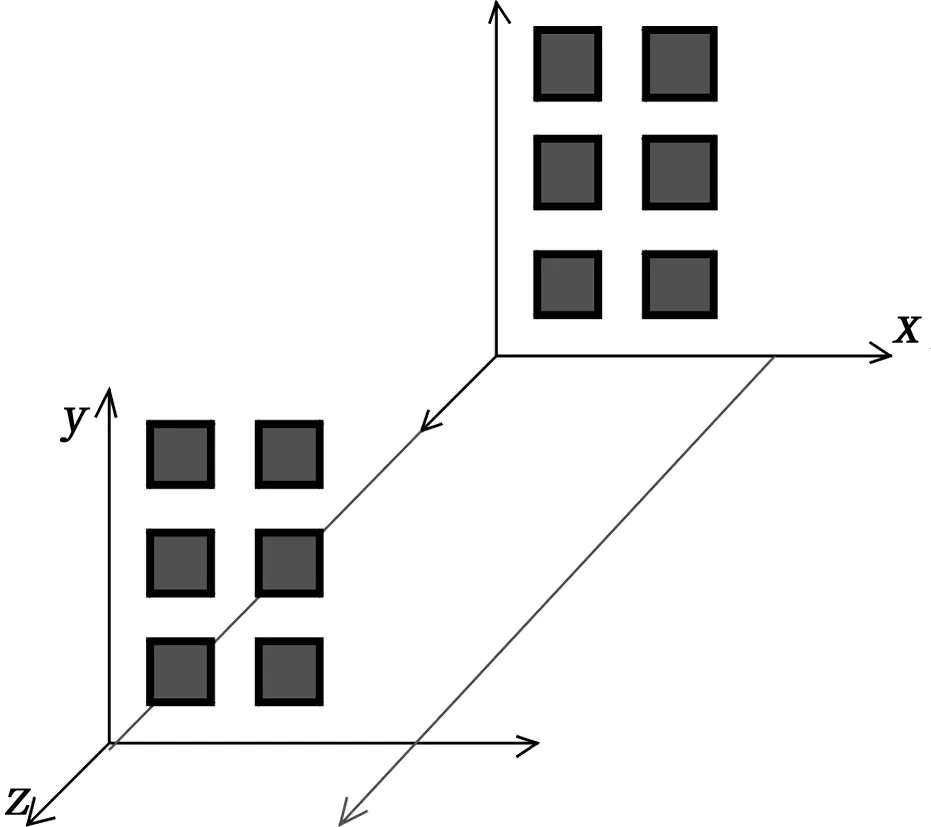
图4 三维拓扑结构示意图

将X方向分为2块，Y方向分为3块，Z方向分为2块，各进程的编号myid的值为0,1,2，…，11。

2.2.2 任意划分区域的实现

为了实现计算域能够在3个方向上的任意划分，最关键的就是要解决网格在3个方向的整除问题。所以需要在无法被整除的方向上附加一些网格，以X向为例，附加网格的数量如式3所示：

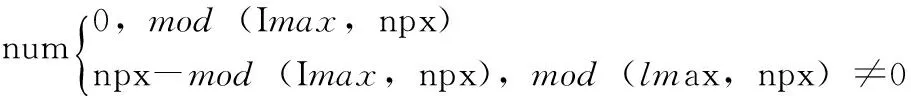
(3)

附加网格不参与数据计算，只进行存储和通信。但在进行计算域划分的时候，还是应尽量保证整除，因为这样设计的程序会较为简单。

2.2.3 子区域的通信

本文设计的并行化算法需要实现计算域3个方向上的任意划分，但其仅能保证一个方向上的数据连续通信，其它两个方向的数据通过MPI函数库的MPI_TYPE_HVECTOR的自定义数据类型来处理。其调用形式如下：

MPI_TYPE_HVECTOR(COUNT,BLOCKLENGTH,STRIDE,OLDTYPE,NEWTYPE,IERROR)

其中，COUNT表示整合数据的块数，BLOCKLENGTH表示每个子区域中所含元素的个数，STRIDE表示各子区域起始位置间的字节数，OLDTYPE表示旧的数据类型，NEWTYPE表示新的数据类型。

由于Y，Z方向的数据均不连续，以yz平面为例，用户通过自定义一个数据类型，将Y、Z方向的不连续数据进行打包，使他们能够进行正常通信。具体代码如下：

MPI_Type_Hvector (mysizey,1, (mysizex+2)*8,

MPI_R eal8,Txx,ierr) MPI_Type_Hvector(mysizez,1,(mysizex+2)*(mysizey+2)*8,Txx,Tx,ierr)

MPI_Type_commit(Tx,ierr) MPI_Type_free(Txx,ierr)

其中，Txx表示y方向的一组数据，其为最终Tx数据的中间过渡值，在完成最终的数据类型定义后，需将中间过渡的数据类型释放掉。

2.3 并行后处理

并行计算的后处理主要包括对关键点的数据采集、可视化软件的接口设计方面。针对不同的需求可编制不同的后处理程序，本文编制的后处理程序可将并行计算后的结果显示出来，满足所需的后处理要求。

3 并行程序设计及性能分析

3.1 并行程序设计

本文设计的并行程序，由主程序、前处理初始化程序、边界条件处理子程序和主循环计算子程序组成[7]，各部分的功能如下所示。

1)主程序：程序的核心构成，贯穿于程序的整个执行过程，完成各子程序的调用，采用最节简的语言设计；

2)前处理初始化程序：主要完成人机交互，能让用户选择计算的种类，并进行有关参数的设置。同时要完成并行计算循环的起始位置设置，各进程的位置及与其相关进程的编号；

3)边界条件处理子程序：处理计算模型的压力，速度，网格标志，介质标志等物理量的边界条件；

4)主循环计算子程序：主循环程序包括人工粘性步、Lagrange步、Euler步、修正步和输出子程序组成。其中，人工粘性步用来计算人工粘性、损伤度和偏应力等；Lagrange步用来计算压力梯度对质团的速度、能量、动量和比内能的影响；Euler步使用改进的Youngs界面处理方法对能量、质量、体积和动量进行输运；修正步子程序主要对计算的数值进行修正，以保证计算能够继续保持下去；输出子程序主要完成计算结果的二维、三维切片输出。

整个并行程序的执行流程如图5所示。

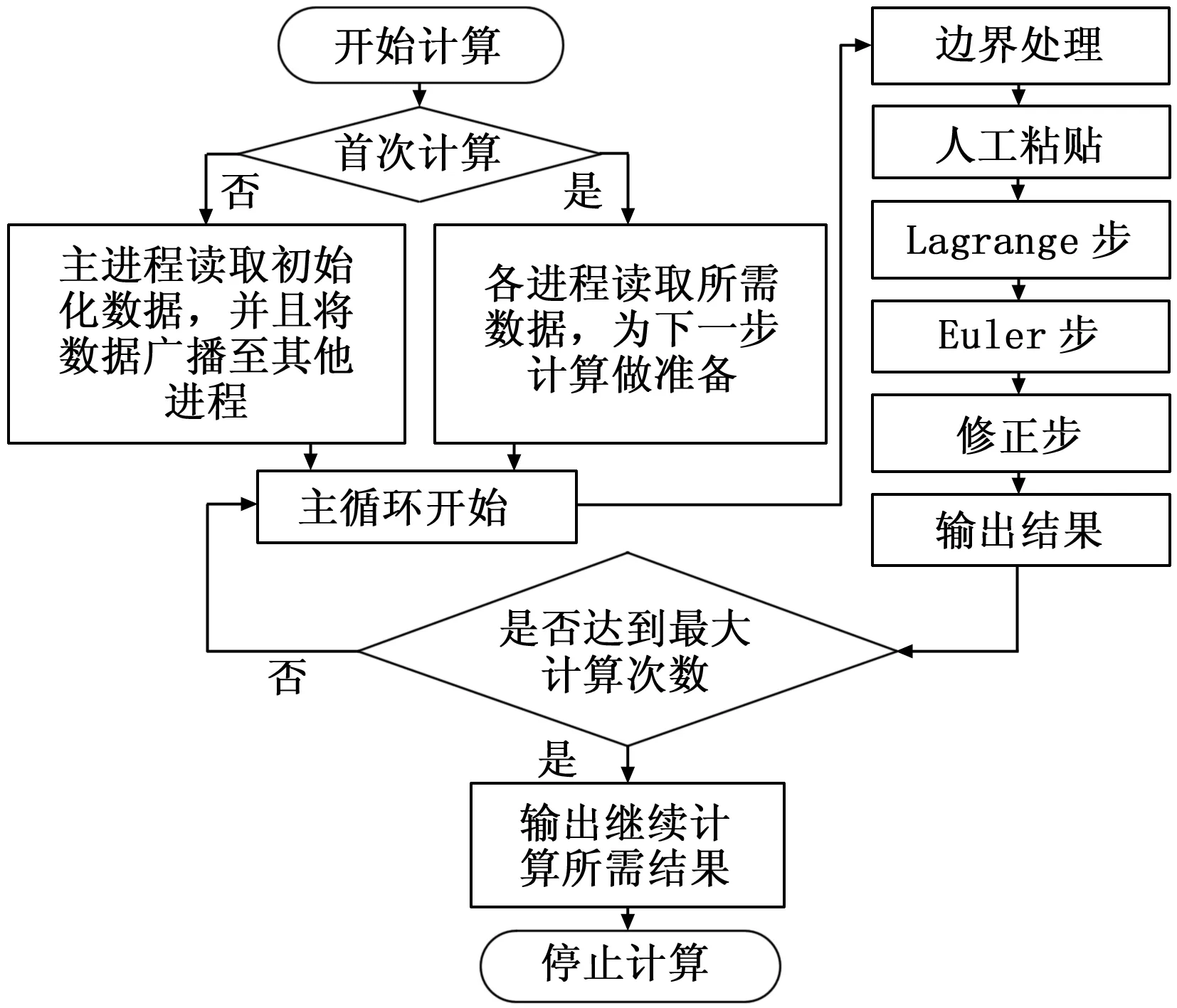
图5 程序执行流程图

3.2 性能分析

1)并行性能测试

选取三介质聚能射流模型[8]为测试算例，处理92×92×300、151×151×200、151×151×300和200×200×300 4个不同网格数的模型，分别记为1，2，3，4号模型。测试共分为8个区，计算步骤为5 000步，取每100步所需的时间作为其运行的平均速度。各模型的加速比如表1所示。

从表1中可以看出：

①同一模型中，分区越多的计算速度越快；

②不同网格模型中，网格数越多，其加速比也越高。

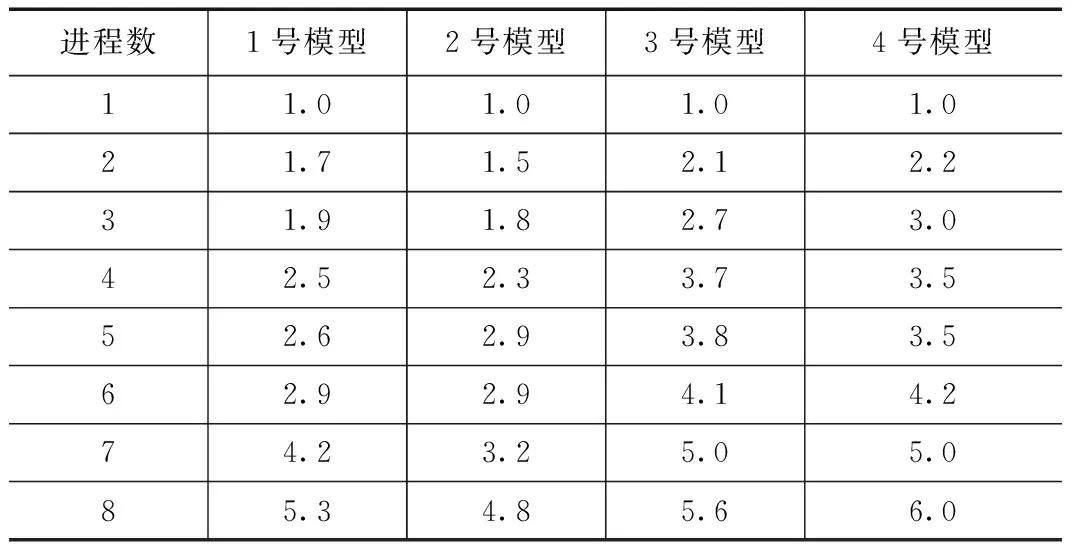
表1 不同模型的加速比

2)不同分区的算例测试

选取空中爆炸模型，炸药类型为TNT，装药密度为1.65 g/cm3，装药半径为1 m，装药量为6.9 t，爆速为6.970 mm/ μs，空气密度为1.29 × 10-3g/cm3。分区统一划分为1×1×1，1×3×1，1×1×3和3×1×1四种模型，其中1×1×1模型算例等价于于串行算法，而其它模型代表3种不同的分区方法。

对算例1及算例2进行全局监测，对算例3采用10个关键点进行压力监测。测试结果表明：算例1、算例2爆炸在各分区的检测结果基本一致，分别如图6、图7所示。

图6 算例1的二维切片结果

图7 算例2的二维切片结果

算例3的10个关键点各分区的压力测试结果如表2所示。

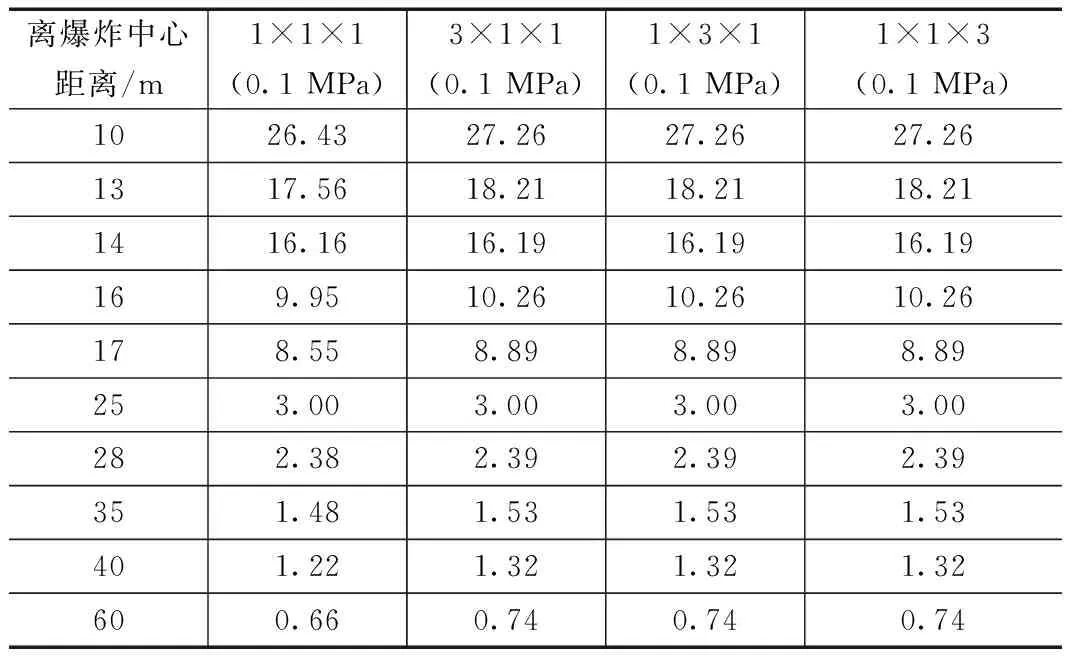
表2 算例3不同分区的冲击波峰值超压值

由表2中可以看出，1×3×1，1×1×3和3×1×13个分区关键点的空中爆炸冲击波波峰数值完全一致，但却与1×1×1的划分区域有些许区别，主要原因如下：1)网格的划分会使串行计算数值和并行计算数值有一定的误差；2)程序设计中，很多网格介质标志的判定方法比较粗糙存在误判问题。

从上述的算例测试可以看出，不同的分区不会对计算结果产生影响，证明了程序可以对计算域进行任意划分。

4 程序的实例仿真

4.1 空中爆炸

选取炸药类型为TNT，装药密度为1.65 g/cm3，装药半径为1 m，装药量为6.9 t，爆速为6.970 mm/μs，空气密度为1.29×10-3g/cm3，爆轰产物的多方指数k0取3，爆轰产物充分膨胀下的多方指数k1取3.16，边界条件为连续性边界，计算区域大小为100 m×10 m×10 m，网格划分为400×40×40。

根据前人大量的实验，空中爆炸冲击波峰值的超压计算公式如式3所示：

(3)

式中，ΔPm表示空气冲击波波峰超压(0.1 Mpa)，w表示装药量(kg)，r表示距爆炸中心的距离(m)。根据式(3)及本文设计程序的数值模拟后的结果如表3所示。

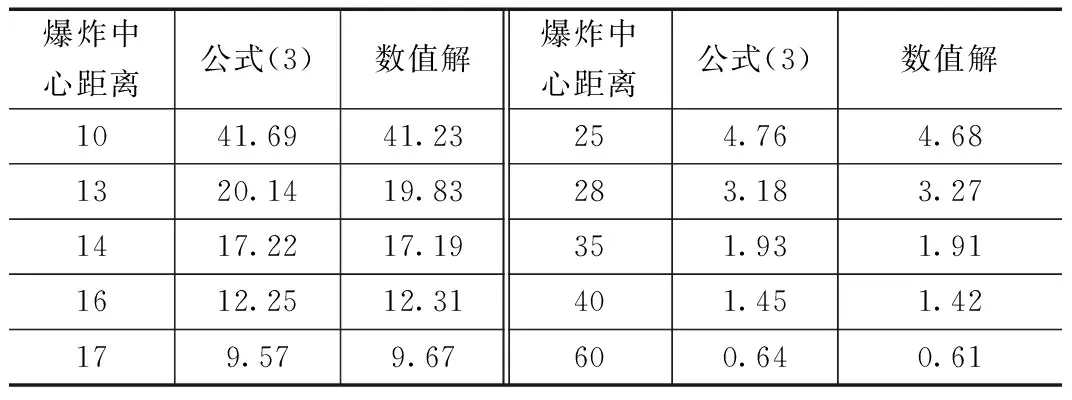
表3 冲击波峰值超压数值解和经验公式解的比较

从表中可以看出，本文设计的程序数值计算结果与前人的实验结果基本一致，说明了本文所设计算法及程序的正确性。

4.2 聚能射流

选取的计算模型药型罩为等壁厚锥形，厚度2 mm，材料45#钢，药柱的锥形角120°，高33 mm，直径40 mm，边界条件为连续性边界，计算域大小为46 mm×46 mm×150 mm，网格步长为0.5 mm。

应用本文所设计程序的模拟结果如图9所示。

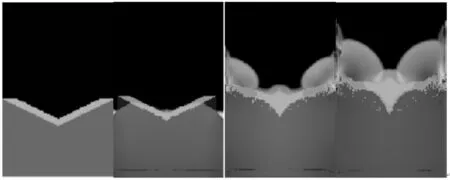
图9 聚能射流二维切片的程序模拟图

实际的聚能射流如图10所示。

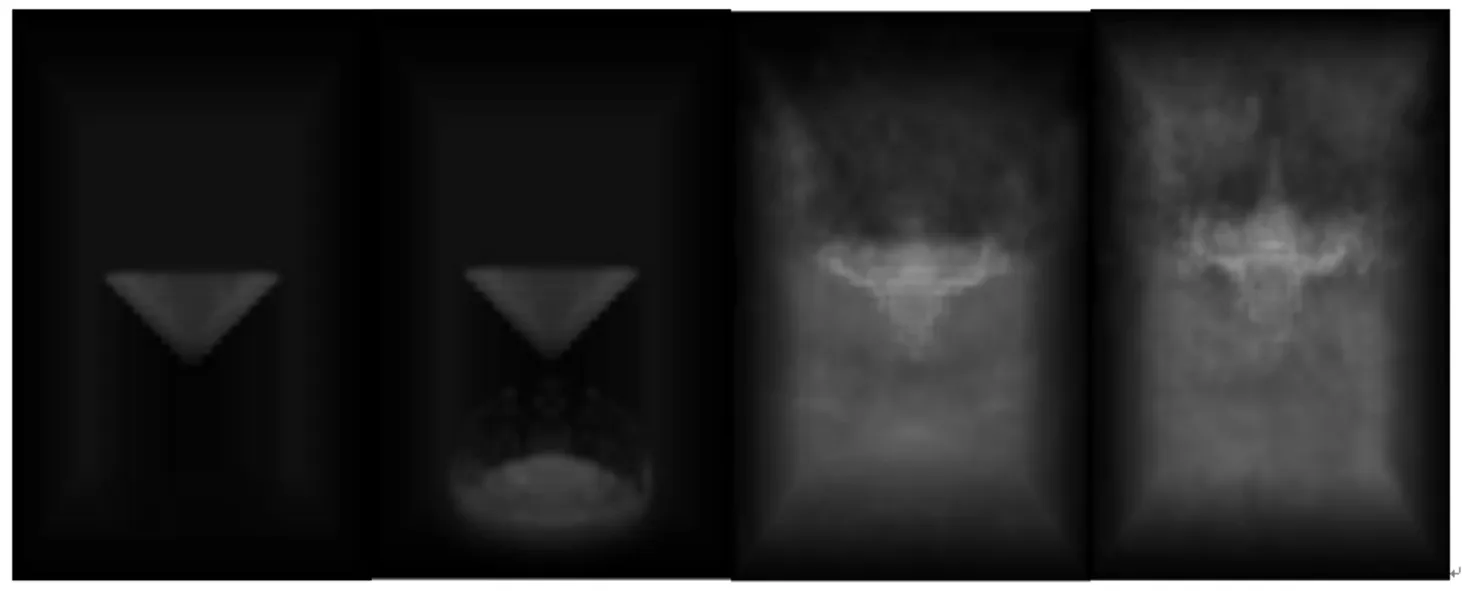
图10 聚能射流的实际效果图

从图9的程序模拟结果可以清楚地看出，聚能射流过程中共有3种介质交互作用，相互之间界面清晰，说明改进的Youngs算法的界面处理是非常精确的。

从图9和图10中可以看出，在金属射流不断伸长的过程中，从头部到尾部，速度逐渐减小，且图9的模拟结果和图10的实验结果基本一致，证明了算法及程序的正确性。

5 结论

本文设计了基于改进Youngs界面处理技术的Euler并行算法，并采用MPI标准消息传递接口编制了流体弹塑性动力学的并行程序，然后对程序进行了并行性能分析和算例测试，结果表明并行算法对程序的加速比有较大的提高，而不同分区对并行算法的计算结果没有影响。最后通过对空中爆炸和聚能射流的实例仿真，证明了并行算法及程序的正确性，对爆炸冲击问题的研究具有重要意义。

[1] Zhang W Y, Ma T B, Ning J G. Visualized computing for explosion disasters, progress in safety science and technology (Vol. VI)[M].Science Press, 2012:1214-1218.

[2] Wang G, Wang J T, Liu K X. New numerical algorithm in SUPER CE/SE and their application in explosion mechanics[J]. Science China Physics,Mechanics& Astronomy. 2011,52(2): 237-243.

[3] 马天宝, 费广磊, 张文耀. 三维多物质弹塑性流体动力学 Euler 方法的并行算法研究及程序测试[J].高压物理学报, 2011,25(6): 508-513.

[4] 马天宝, 郝 莉, 宁建国. Euler 多物质流体动力学数值方法中的界面处理算法[J]. 计算物理, 2012, 25(2): 133- 138.

[5] 夏 锐, 肖明清, 赖 根. 并行测试系统设计与开发[J]. 计算机测量与控制, 2015, 14(7):841-843.

[6] Ning J G, Ren H L, Li P. Mechanical behaviors and damage constitutive model of ceramics under shock compression [J]. Acta Mechanica Sinica, 2011, 24(3): 305-315.

[7] 王生武, 石秀华. 涡轮叶尖压力边小翼肋条对泄漏流场的数值模拟[J]. 计算机测量与控制, 2009,17(8):1527-1530.

[8] 费广磊, 马天宝, 宁建国. 基于 MPI 的聚能射流问题的并行计算[A]. 中国力学学会2012 学术大会论文集[C]．2012.

3D More Material Euler Interface Processing Parallel Algorithm Research

Long Wenjia，Li Yuexin

(Computer and Information Engineering Department, Hubei University, Wuhan 430000,China)

Of explosion shock in view of the existing algorithms can not effectively study this problem, on the basis of the technology improved the Youngs interface design for more than three dimensional material Euler interface processing parallel algorithm. Then using MPI standard to the program design of the algorithm and program for the parallel performance testing and different partitions example test, the test results show that the parallel algorithm for acceleration is larger, the different partition has no effect on the calculation results of parallel algorithm. Finally application programs written by the air blast and shaped jet are simulated, the results show that the simulation results and the program is conform to the predecessors' research data, illustrates the effectiveness of the program.

explosion and impact;numerical simulation; Euler's method; parallel computing; youngs interface technology

2015-08-27；

2015-09-25。

湖北省科技支撑项目(2014BAA089)。

龙文佳(1978-)，女，湖北荆州人，讲师，硕士，主要从事数据库方向的研究。

李跃新(1958-),男，湖北武汉人，副教授，博士，主要从事知识工程与并行计算方向的研究。

1671-4598(2016)06-0226-04

10.16526/j.cnki.11-4762/tp.2016.06.062

TM417

A