基于馈线零序阻抗特性的谐振接地故障选线方法

汤 涛 黄 纯 江亚群 罗勋华 刘鹏辉



基于馈线零序阻抗特性的谐振接地故障选线方法

汤 涛 黄 纯 江亚群 罗勋华 刘鹏辉

（湖南大学电气与信息工程学院 长沙 410082）

谐振接地配电网发生单相接地故障后，健全线路的零序阻抗在最小串联谐振频率以下的各频段呈电容特性；故障线路的零序阻抗在高频段呈电容特性，在低频段呈电感特性。依据这一现象，提出一种基于馈线零序阻抗特性的故障选线方法。通过低通和带通数字滤波器提取母线零序电压和各馈线零序电流的高频分量和低频分量，并分别对母线零序电压的高频分量和低频分量求导。由于容性线路的电压导数与电流的比值为定值，故母线零序电压导数与健全线路零序电流的比值在高频段与低频段相等，其实际差值近似为0；母线零序电压导数与故障线路零序电流的比值在高频段与低频段不等，其差值较大，据此构成故障选线判据。理论分析和仿真结果表明，该方法选线准确、可靠且适应性强。

谐振接地系统 故障选线 馈线 单相接地 零序阻抗

0 引言

谐振接地系统发生单相接地故障时，由于故障电流微弱、零序电流方向不定、电磁干扰严重、故障状况复杂等原因，往往造成故障选线不准确[1,2]。故障发生后短期内有幅值较大的暂态量，利用暂态信号进行故障选线具有灵敏度高、受消弧线圈影响小等优点，故基于暂态信号的故障选线得到了人们的广泛关注[3-7]。随着小波分析理论的出现，利用暂态能量相关的选线方法开始受到重视，小波能量选线往往需要提取能量最集中的故障特征频带，而特征频带会随故障状态、系统结构的不同而漂移不定，能量选线法易发生误判。自适应能量选线法能较好地解决上述问题[8,9]，但利用单一特征频带进行故障选线，舍弃了其他频带的故障信息，选线仍可能发生误判。文献[10,11]利用故障后线路是否含有暂态衰减直流分量来区分故障线路与健全线路，文献[10]直接计算各馈线电感暂态衰减直流分量的数值实现选线，文献[11]利用电感衰减直流分量和基频分量重构信号的能量比进行选线，两者均忽略了丰富的暂态故障高频信息；此外，这两种选线方法需结合其他暂态选线法。文献[12-14]利用相关分析法进行故障选线，原理上只利用了故障暂态信号的高频分量，没有考虑低频故障信息。粗集理论法[15]、形态学法[16]、层次聚类法[17]、模糊算法[18]、融合算法[19]等故障选线方法都具有一定的参考价值，但除了依赖数学工具外，更应该考虑故障信号或故障馈线本身的特点来鉴别故障线路。文献[20,21]利用配电网系统串联谐振频率以下频段的馈线阻抗特性进行故障选线，且经消弧线圈接地时滤除了影响选线的低频段分量（3~4倍工频以下的分量），在过渡电阻较小或故障合闸角较大时，具有较高选线准确率。

本文在文献[20,21]的基础上，探讨故障线路零序阻抗在高、低频段的特性差异，由此提出一种基于馈线零序阻抗特性的故障选线方法。该方法根据母线零序电压导数与馈线零序电流的比值在高频段和低频段是否相等来进行故障选线，充分利用了各馈线不同频段的暂态信息，故障选线准确率得到提高。仿真结果证明了该方法的有效性。

1 配电网馈线零序阻抗特性

配电网谐振接地系统发生单相接地故障时，其零序等效网络如图1所示，此时，开关S闭合，消弧线圈产生电感电流抵消接地点的零序电容电流。0k、0k、0k分别为馈线（=1,2,…,）的单位长度零序电感、电阻和分布电容，s、s分别为消弧线圈电感和串联电阻，i为流经消弧线圈的电流，0k为馈线的零序电流，0为母线零序电压，为馈线出线数。

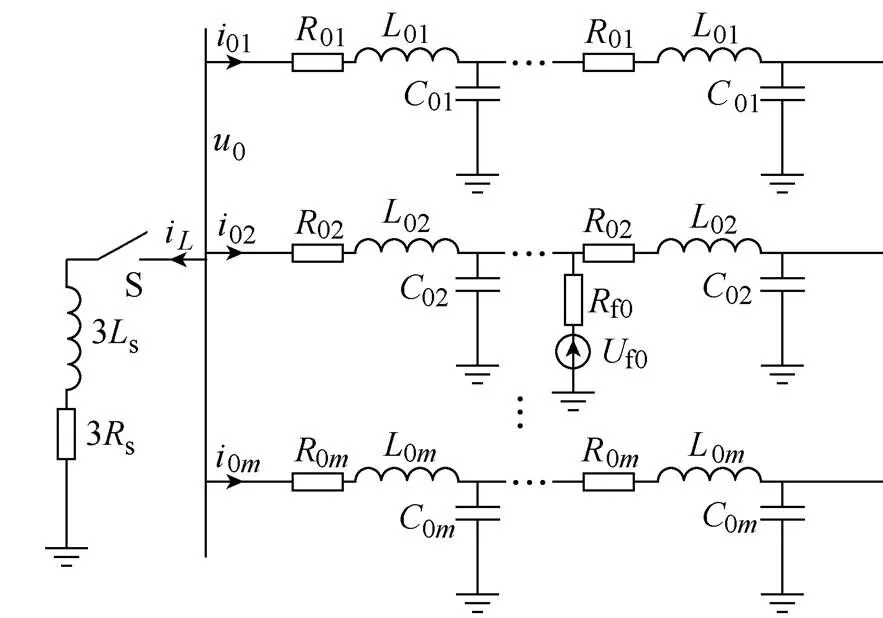
图1 单相接地零序等效网络

正常情况下，当均匀线路末端开路时，该线路的入端阻抗（端口电压与电流的比值）()为

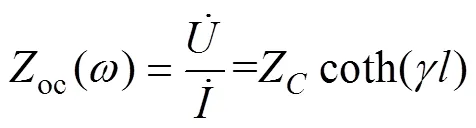
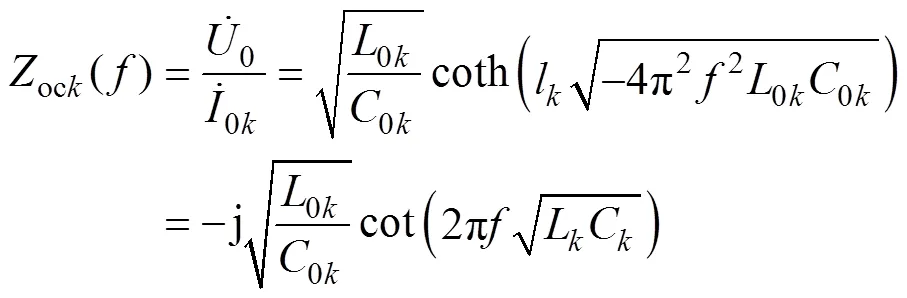
若选取最小串联谐振频率min为各馈线首次发生串联谐振频率f的最小值，即

故障情况下，设图1中馈线2为故障线路，对于健全线路，端口检测阻抗为自身线路的入端零序阻抗。根据上述分析可知，在频段内健全线路（≠2）可等效为一集中参数电容，即在该频段内健全线路的零序阻抗Z可表示为

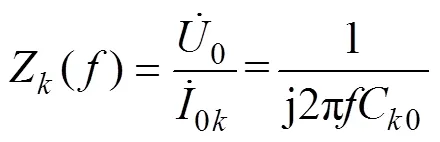
式中，C0为馈线的等值电容。

将健全线路用其等值电容代替，故障线路保持不变，则图1可简化为图2。

图2 简化零序网络

式中，s为配电网消弧线圈的电感。

由式（5）可知，当频率从0逐渐增大时，馈线入端零序导纳/阻抗从感性逐渐过渡到容性。当时，系统发生并联谐振，设此谐振频率为。谐振接地系统消弧线圈一般采用5%～10%的过补偿，工频下的电感阻抗约等于所有线路的零序容抗，故一般略大于工频。显然，＜＜。当时，故障线路零序阻抗呈感性；当时，故障线路零序阻抗呈容性。

上述分析中，假设各馈线末端是开路的，实际线路末端是接有配电变压器和负荷的。由于变压器一次侧不接地，不能流通零序电流，即零序阻抗为无穷大，可看作开路。换言之，变压器和负荷并不影响上述分析的入端零序阻抗，即配电变压器不影响馈线零序电流和母线零序电压。图3为系统故障时配电变压器对某健全馈线和故障馈线零序电流的影响。由图3可知，在带有和不带配电变压器时，馈线零序电流波形几乎是重合的。

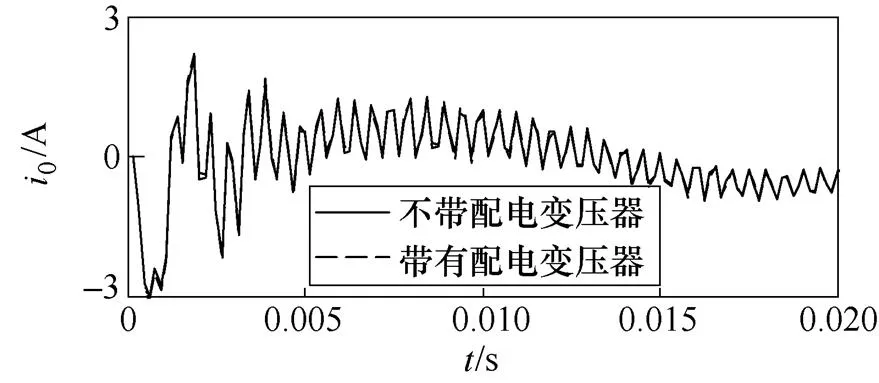
（a）健全线路

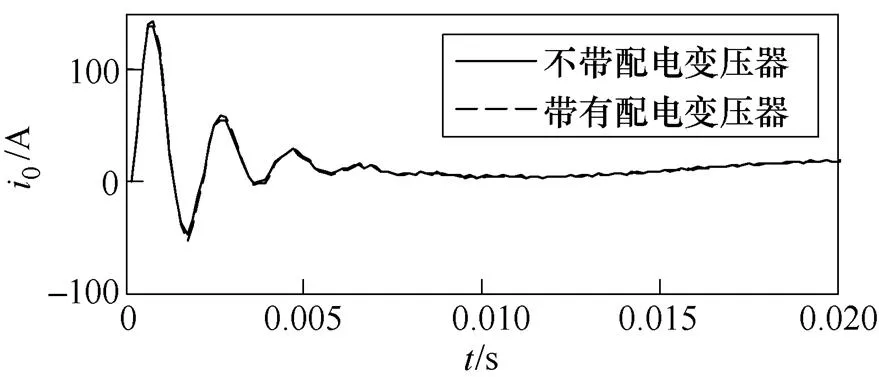
（b）故障线路

图3 配电变压器对健全线路和馈线零序电流的影响

Fig.3 Influence of distribution transformer to good and faulty feeder zero sequence currents

综上所述，对于健全线路，零序阻抗在各频段均呈电容特性；对于故障线路，等值零序阻抗在高频段呈电容特性，在低频段呈电感特性。

2 基于馈线零序阻抗特性的选线原理

设馈线2为故障线路，其余馈线为健全线路。根据故障线路与健全线路零序阻抗特性的差异，构成故障选线原理。

对于健全线路（≠2），其零序电流与母线零序电压导数在高频段和低频段的分量满足

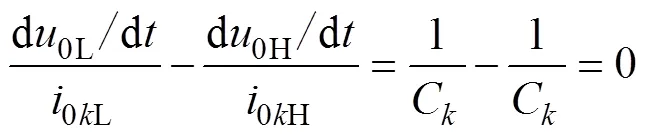
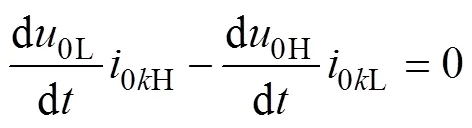
定义

则健全线路满足

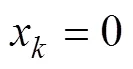
对于故障线路2，其零序阻抗特性在高频段呈容性，设其等值电容为，结合式（5）有

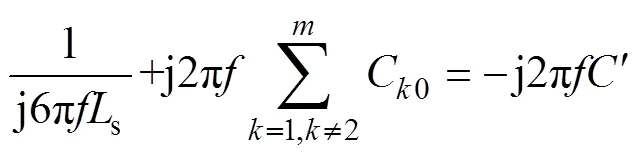
由式（10）、式（11）得

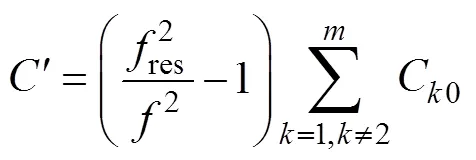
由式（13）可知，故障线路在高频段几乎不受消弧线圈影响，则高频段的零序电流为

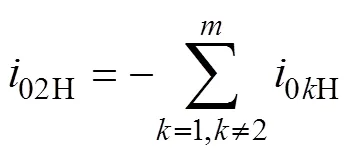
由文献[9]可知，暂态过程中，故障线路零序电流在低频段主要包含基频分量和衰减直流分量，且在故障合闸角为0°时衰减直流分量最大，在故障合闸角为90°时该分量几乎为0。母线零序电压在低频段仅有基频分量。

根据故障线路在高低频段的阻抗特性，得到故障线路零序电流及母线零序电压在高低频段的关 系为

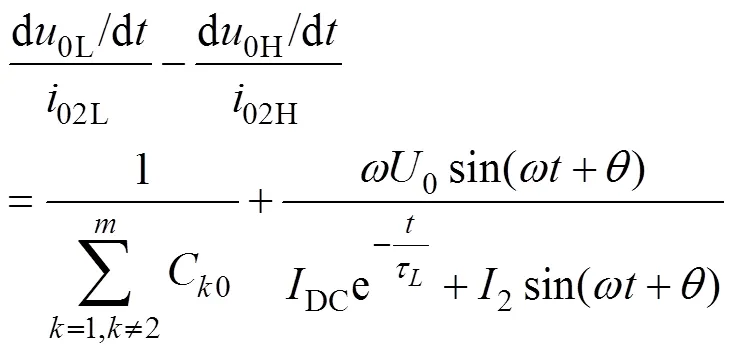
式（15）中，母线零序电压导数与馈线零序电流的比值在高频段为定值，在低频段为时间函数，两者显然不等，即式（15）不等于0，两侧同乘，得到故障线路2满足

综上所述，健全线路x=0（≠2）；故障线路2≠0。

对健全线路，在给定数据窗内，x的所有数值都为0，故其方均根也为0，由于电网三相不平衡、测量误差、噪声干扰等因素的影响，实际方均根为接近0的较小数值。故障线路在给定数据窗内x实际上大多数远大于0，x的方均根值也远大于0。二者差异显著，由此构成故障选线判据，可靠性高。具体实现时，可通过求各馈线在给定数据窗内x的方均根选出故障线路，也可通过能量法实现，本文选用方均根进行故障选线。

由于架空线路和电缆线路的x相差较大，为避免母线故障时选线发生误判，采用馈线x的方均根与其零序电流的方均根的比值作为故障选线判断量。

3 故障选线步骤

根据上述分析，基于馈线零序阻抗特性的故障选线流程如图4所示。具体实现步骤如下。

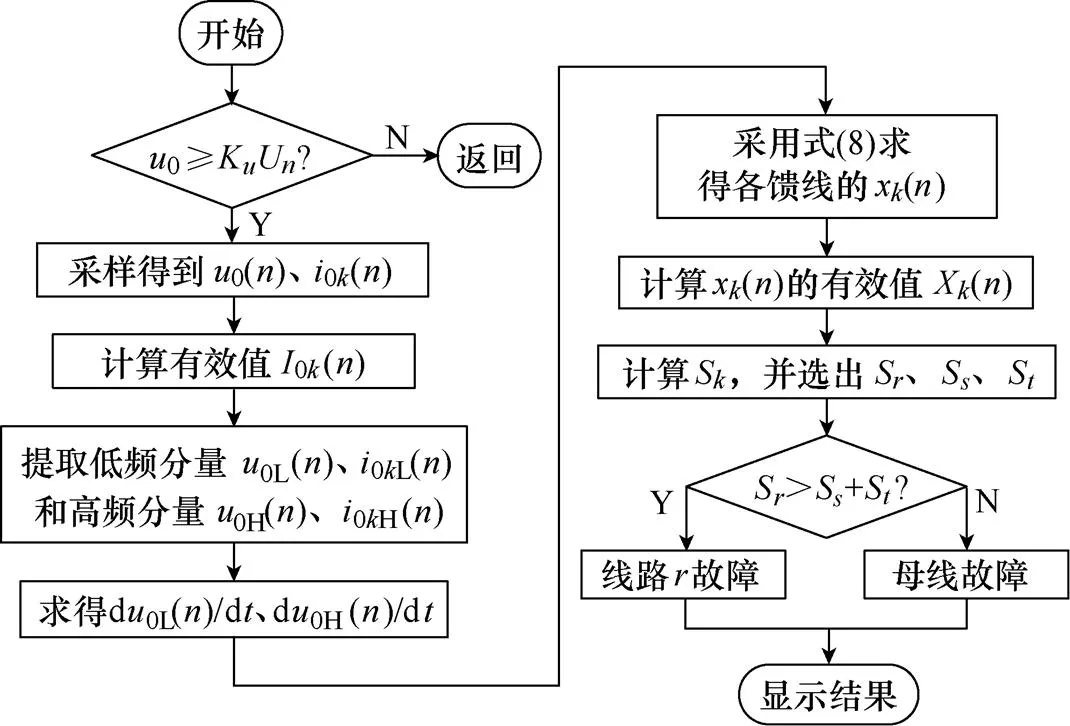
图4 故障选线流程

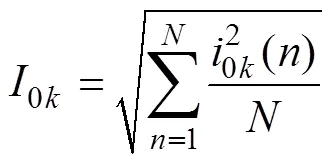
（4）利用差分法分别对母线零序电压的高频分量和低频分量求导，得到相应的零序电压导数和。

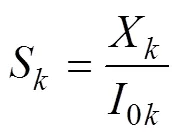
4 仿真

4.1 截止频率的选取

本文选用切比雪夫滤波器来设计低通、带通数字滤波器，滤波器的阶数分别为6和19，其幅频特性如图5所示。为了更有效地提取暂态信号低频分量和高频分量，截止频率的选取至关重要。根据第1节的分析，低频段截止频率的选取与故障线路的等值导纳有关，而故障位置和故障线路未知，无法确定并联谐振频率的具体值，但可求得谐振频率的范围。当分布电容最小的馈线发生故障时，求得系统最小并联谐振频率；当分布电容最大的馈线发生故障时，求得系统最大并联谐振频率。因此，低频段的截止频率可取为最小并联谐振频率与最大并联谐振频率之间的某一数值。由式（5）可推出、分别为

图5 低通、带通数字滤波器的幅频特性

高频段故障截止频率的选取与最小分布电容健全线路有关，而由于故障线路未知，则选取所有馈线首次串联谐振频率的最小值为一截止频率，该频率的具体计算如式（3）所示，另一截止频率可取为。

实际上，为了避免低频分量和更高频段分量对高频分量的影响，高频段的两侧截止频率可分别向高频段的中间频率靠近。具体来说，低频段的截止频率的取值略大于；高频段的截止频率可取为的3～4倍，可取为实际值的2/3。

4.2 仿真

谐振接地系统仿真模型如图6所示。该系统为6出线的110kV/10kV变电所，其中线路1、2为电缆线路，其余为架空线路，具体线路长度标示于图6中。开关S闭合，中性点经消弧线圈接地，本文采用10%的过补偿，消弧线圈的有功损耗取为无功损耗的5%。负荷有功功率统一为1MW，功率因数为0.89，其模型为三相对称线性负荷。电缆线路零序参数为0=2.7W/km，0=1.02mH/km，0=0.28mF/km；正序参数为1=0.27W/km，1=0.255mH/km，1= 0.339mF/km。架空线路零序参数为0=0.25W/km，0=0.54mH/km，0=0.012mF/km；正序参数为1= 0.178W/km，1=1.21mH/km，1=0.015mF/km。

图6 谐振接地系统仿真模型

系统采样频率设定为6.4kHz。根据4.1节的分析，低频段的截止频率取为60Hz，高频段的截止频率取为200～1 000Hz。故障发生后，母线零序电压显著增大并启动故障选线，通过采样记录故障后两个周期的馈线零序电流及母线零序电压。本文对不同馈线不同故障状态的单相接地故障进行了仿真，结果见表1，其中，f为故障距离，f为过渡电阻，为故障合闸角。

表1 不同馈线不同故障状态的选线结果

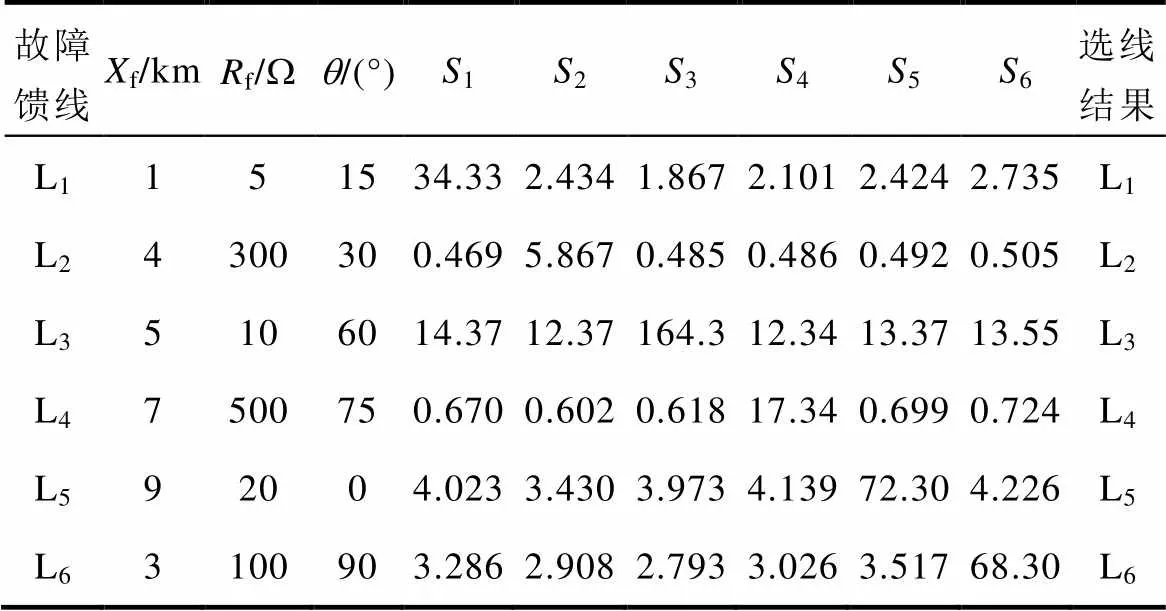
Tab.1 Selection results of different failure modes and different lines

表1中馈线3故障后，各馈线零序电流及母线零序电压采样波形如图7所示。由图7可见，电缆线路的零序电流幅值较大，而架空线路的零序电流幅值偏小，由于消弧线圈的补偿作用，故障馈线的稳态零序电流较小。

图7 馈线零序电流和母线零序电压

通过低通、带通数字滤波器分别提取图7采样信号的低频分量和高频分量，并利用式（8）求得各馈线的x，结果如图8所示。由于低通滤波器截止频率选取较低，相比原信号，低频分量有较大的输出延迟，约为0.005s，但所有低频分量的输出延迟相当，故不影响故障选线结果。

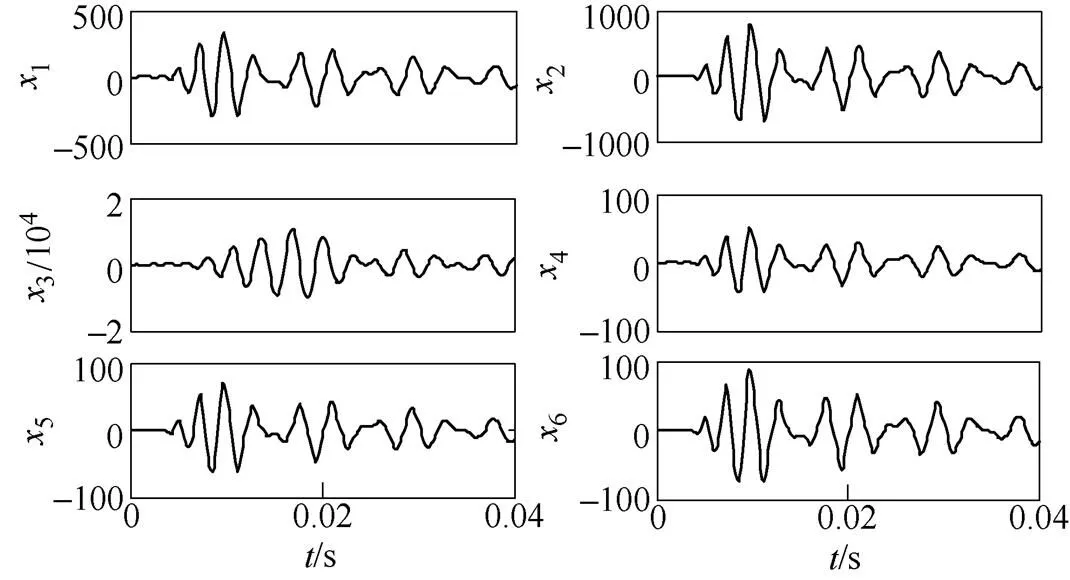
图8 Sk曲线

在两个工频周期的数据窗内，得到图8中各馈线x值的方均根X分别为105.5、243.2、3670、15.76、17.72和19.43，并得到图7中各馈线零序电流的方均根0k分别为7.336、19.66、22.34、1.277、1.326和1.434，最后得到二者对应的比值S分别为14.37、12.37、164.3、12.34、13.37和13.55。显然，3远大于其他S（≠3），易知馈线3为故障线路。

若数据窗为时间段0.005～0.045s，算得各馈线的S值分别为14.40、12.40、165.3、12.38、13.40和13.58。对比可知，低通滤波器的输出延迟不会影响选线结果。

为使馈线零序电流更接近实际情况，现减小线路零序电容并改变个别线路长度、线路类型进行仿真，其采样零序电流如图9所示，x值如图10所示，并算得S分别为10.27、9.948、69.23、10.02、9.479和10.19，故馈线3为故障线路，由此表明该选线方法仍然适用。实际上，由于本文所提算法采用的参数S是X与0k的比值，因此避免了线路零序电容大小、线路长度及线路类型对本方法的影响。

图9 馈线零序电流

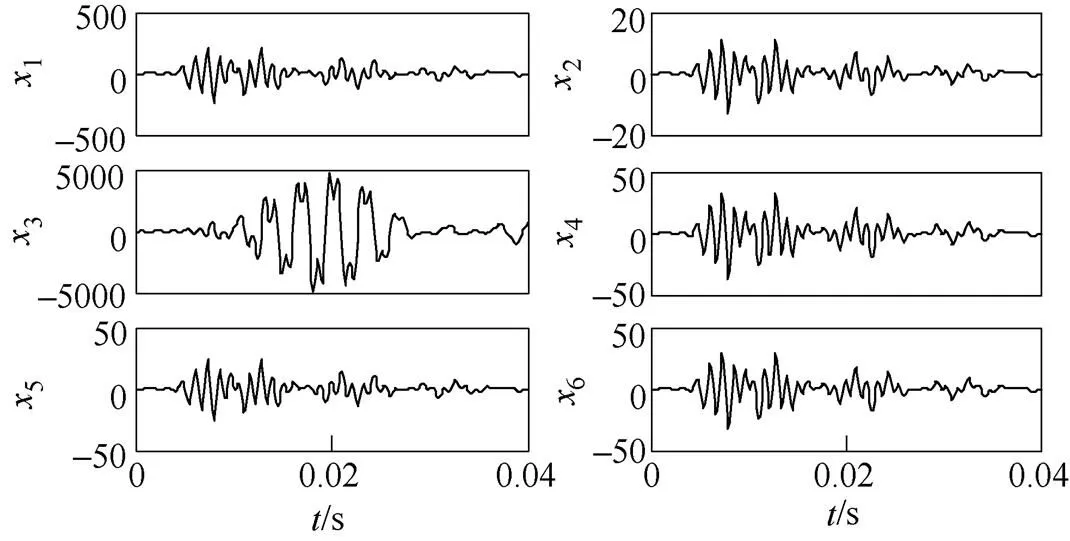
图10 各馈线Sk

5 选线方法的适用性

5.1 过渡电阻的影响

架空线路3距母线3km处在故障合闸角为45°时发生单相接地故障，本文就不同过渡电阻进行了仿真，结果见表2。由表2可知，随着过渡电阻的增大，各馈线的S均逐渐减小，但任何过渡电阻下，故障线路的S均明显大于其他馈线的S，且其他馈线的S相差甚小，故能准确、可靠地实现选线。

当过渡电阻为5W时，2、3分别为11.79、162.1；当过渡电阻为500W时，2、3分别为0.432、13.77。从不同过渡电阻下二者的比值可知，在较大过渡电阻下的选线灵敏度较高。

表2 不同过渡电阻下的选线结果

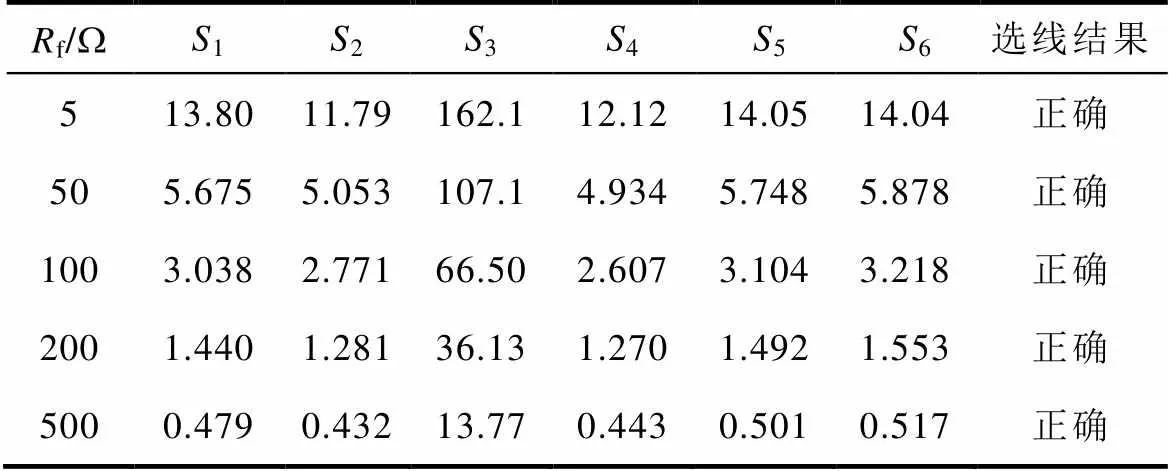
Tab.2 Selection results with different transition resistances

5.2 故障合闸角的影响

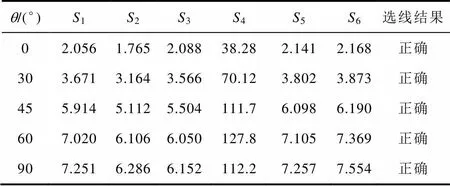
在不同故障合闸角的情况下，架空馈线4距母线5km处发生过渡电阻为50W的单相接地故障，仿真结果见表3，表明该选线方法能适用于不同故障合闸角的情况。

表3 不同合闸角情况下的选线结果

Tab.3 Selection results with different initial fault angles

当故障合闸角为0°和90°时，3、4分别为2.088、38.28和6.152、112.2，显然，两种情况下的灵敏度相当。即当故障合闸角为0°时，选线灵敏度几乎没有下降。

5.3 不同故障距离的影响

表4为不同故障距离的仿真结果，故障线路为馈线6，其故障合闸角为60°时，接地电阻为100W。由表4可知，各馈线的S几乎不受故障距离的影响，而故障线路的S与健全线路的S差异显著，选线灵敏、可靠。

表4 不同故障距离的选线结果

Tab.4 Selection results with different fault distances

5.4 母线故障的选线结果

本文就不同过渡电阻、不同故障合闸角情况下发生母线故障进行了仿真，结果见表5。数据表明母线故障时能准确实现故障选线。

表5 母线故障选线结果

Tab.5 Selection results of bus fault

5.5 噪声的影响

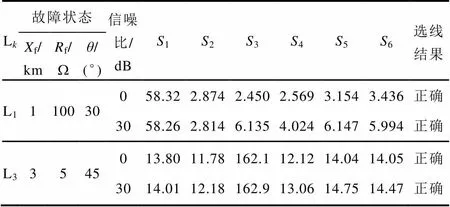
电缆线路L1和架空线路L3在不同故障状态下，加入30dB高斯白噪声与不加噪声的单相接地故障仿真结果见表6。由表6可知，在过渡电阻较小时，噪声叠加对各馈线S的影响甚微；过渡电阻较大时，噪声叠加使得健全线路的S增大，故障选线灵敏度降低，但故障线路与健全线路的S仍有较大差距，故能准确实现选线。

表6 加入高斯白噪声后的选线结果

Tab.6 Selection results with Gaussian white noise

5.6 数据窗长度的影响

馈线5距母线5km处在故障合闸角为60°时，发生过渡电阻为30W的单相接地故障，本文就不同数据窗下进行了仿真，结果见表7。表7中，为1个工频周期。

表7 不同数据窗下的选线结果

Tab.7 Selection results of different data windows

数据窗长度由1个工频周期逐步增加到5个周期，仿真结果表明，数据窗为1个工频周期时，选线灵敏度最低；数据窗增加1个周期时，选线灵敏度显著增加；数据窗从两个周期逐渐增加时，选线灵敏度虽有增加，但幅度不大。考虑到数据窗越长，选线所需存储记忆功能越强，综合考虑，本文选取长度为两个工频周期的数据窗。

5.7 不同补偿度下的选线结果

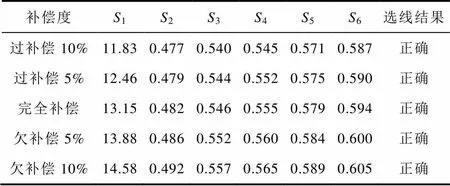
馈线1距母线2km处，在故障合闸角为30°时发生过渡电阻为300W的单相接地故障，并就消弧线圈在过补偿、完全补偿及欠补偿下进行了仿真，结果见表8。仿真数据表明，在不同补偿度的情况下，选线基本不受影响。

表8 不同补偿度的选线结果

Tab.8 Selection results of different compensation degree

6 结论

配电网谐振接地系统发生单相接地后，故障线路与健全线路在高低频段具有不同的馈线零序阻抗特性，由此提出一种基于馈线零序阻抗特性的谐振接地故障选线方法。暂态过程中，母线零序电压导数与健全线路零序电流的比值在高频段和低频段相等；而母线零序电压导数与故障线路零序电流的比值在高频段和低频段不等，二者差异明显。据此构成故障选线判据，可靠性高。该方法充分利用故障后母线和馈线在不同频段的暂态信息，选线准确率高。数字仿真结果表明，该方法不受线路类型及线路长度的影响，具有较强的抗噪声干扰能力，能适用于不同过渡电阻、不同故障位置、不同补偿度和不同合闸角下的故障选线；能提高较大过渡电阻下的选线灵敏度，不降低故障合闸角为0°时的选线灵敏度，有望解决高阻接地及故障发生在相电压过零点附近时选线灵敏度不足的问题。

参考文献：

[1] 薛永端, 徐丙垠, 冯祖仁, 等. 小电流接地故障暂态方向保护原理研究[J]. 中国电机工程学报, 2003, 23(7): 51-56.

Xue Yongduan, Xu Bingyin, Feng Zuren, et al. The principle of directional earth fault protection using zero sequence transients non-solid earthed network[J]. Proceedings of the CSEE, 2003, 23(7): 51-56.

[2] 王朋, 田翠华, 陈柏超, 等. 基于新型磁控消弧线圈的电磁混合消弧及配合选线新方法[J]. 电工技术学报, 2015, 30(16): 173-183.

Wang Peng, Tian Cuihua, Chen Baichao, et al. Electromagnetic hybrid arc suppression and a novel method of feeder selection based on the novel magnetic controlled Petersen coil[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 173- 183.

[3] 张钧, 刘洪星, 何正友, 等. 基于瞬时能量函数的故障选线新方法[J]. 电力系统保护与控制, 2012, 40(14): 1-9.

Zhang Jun, Liu Hongxing, He Zhengyou, et al. A novel fault line identification approach based on instantaneous energy function[J]. Power System Protection and Control, 2012, 40(14): 1-9.

[4] 张淑清, 马跃, 李盼, 等. 基于改进的广义谐波小波包分解和混沌振子的小电流接地系统故障选线[J]. 电工技术学报, 2015, 30(3): 13-20.

Zhang Shuqing, Ma Yue, Li Pan, et al. Application of improved generalized harmonic wavelet packet decomposition and chaos oscillator to fault line detection in small current grounding system[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 13-20.

[5] 金涛, 褚福亮. 基于暂态非工频零序电流的含DG新型配电网的接地选线方法[J]. 电工技术学报, 2015, 30(17): 96-105.

Jin Tao, Chu Fuliang. A fault line-selection method in new distribution network with DG based on transient non-power frequency zero sequence current[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 96-105.

[6] 司瑞琦, 黄翰, 罗建, 等. 基于消弧线圈补偿特征的故障选线新方法[J]. 电力系统保护与控制, 2014, 42(23): 16-22.

Si Ruiqi, Huang Han, Luo Jian, et al. Fault line selection approach based on compensation character- ristic of extinction coil[J]. Power System Protection and Control, 2014, 42(23): 16-22.

[7] 赖平, 周想凌, 邱丹. 小电流接地系统暂态电流频率特性分析及故障选线方法研究[J]. 电力系统保护与控制, 2015, 43(4): 51-57.

Lai Ping, Zhou Xiangling, Qiu Dan. Research on transient-current frequency analysis and faulty line detecting method in indirectly grounding power system[J]. Power System Protection and Control, 2015, 43(4): 51-57.

[8] 张伟刚, 张保会, 胡海松. 应用小波包分析实现配电网单相接地故障选线[J]. 电力系统自动化, 2009, 33(23): 60-64.

Zhang Weigang, Zhang Baohui, Hu Haisong. Application of wavelet packet analysis in phase- to-ground fault detection of distribution networks[J]. Automation of Electric Power System, 2009, 33(23): 60-64.

[9] 吴乐鹏, 黄纯, 林达斌, 等. 基于暂态小波能量的小电流接地故障选线新方法[J]. 电力自动化设备, 2013, 33(5): 70-75.

Wu Lepeng, Huang Chun, Lin Dabin, et al. Faulty line selection based on transient wavelet energy for non-solid-earthed network[J]. Electric Power Auto- mation Equipment, 2013, 33(5): 70-75.

[10] 戴剑锋, 张艳霞, 侯喆. 小波重构算法在配电网接地选线中的应用[J]. 电网技术, 2004, 28(3): 43-47.

Dai Jianfeng, Zhang Yanxia, Hou Zhe. Application of wavelet reconstruction algorithm in phase-to-ground fault detection of distribution networks[J]. Power System Technology, 2004, 28(3): 43-47.

[11] 束洪春, 刘娟, 司大军, 等. 自适应消弧线圈接地系统故障选线实用新方法[J]. 电力系统自动化, 2005, 29(13): 64-68.

Shu Hongchun, Liu Juan, Si Dajun, et al. New adaptive method for fault line selection in non-solidly grounded system[J]. Automation of Electric Power System, 2005, 29(13): 64-68.

[12] 李森, 宋国兵, 康小宁, 等. 基于时域下相关分析法的小电流接地故障选线[J]. 电力系统保护与控制, 2008, 36(13): 15-20.

Li Sen, Song Guobing, Kang Xiaoning, et al. Time-domain fault line selection based on correlation analysis in neutral indirect ground system[J]. Power System Protection and Control, 2008, 36(13): 15-20.

[13] 束洪春, 彭仕欣, 李斌, 等. 基于零序电流激励的谐振接地系统故障选线测后模拟方法[J]. 电工技术学报, 2008, 23(10): 106-113.

Shu Hongchun, Peng Shixin, Li Bin, et al. Simulation after detecting fault line in resonant earthed system through zero sequence current motivation[J]. Transa- ctions of China Electrotechnical Society, 2008, 23(10): 106-113.

[14] 刘谋海, 方涛, 姜运, 等. 基于暂态主频分量相关分析的故障选线方法[J]. 电力系统保护与控制, 2016, 44(2): 74-79.

Liu Mouhai, Fang Tao, Jiang Yun, et al. A new correlation analysis approach to fault line selection based on transient main-frequency components[J]. Power System Protection and Control, 2016, 44(2): 74-79.

[15] 庞清乐, 孙同景, 钟麦英, 等. 基于粗集理论的小电流接地系统故障选线[J]. 中国电机工程学报, 2007, 27(4): 60-64.

Pang Qingle, Sun Tongjing, Zhong Maiying, et al. Fault line detection based on rough set theory in indirectly grounding power system[J]. Proceedings of the CSEE, 2007, 27(4): 60-64.

[16] 高艳, 林湘宁, 刘沛, 等. 基于广义形态开闭变换的小电流接地选线算法[J]. 中国电机工程学报, 2006, 26(14): 1-6.

Gao Yan, Lin Xiangning, Liu Pei, et al. Generalized morphological opening-closing transform based feeder selection algorithm for neutral un-effectual grounded system[J]. Proceedings of the CSEE, 2006, 26(14): 1-6.

[17] 李雅洁, 孟晓丽, 宋晓辉, 等. 基于最优FIR滤波器与层次聚类的配电网单相接地故障选线方法[J]. 电网技术, 2015, 39(1): 143-149.

Li Yajie, Meng Xiaoli, Song Xiaohui, et al. Single- phase-to-ground fault line detection for distribution network based on optimal finite impulse response filter and hierarchical clustering[J]. Power System Technology, 2015, 39(1): 143-149.

[18] 王兴国, 张举. 基于相关分析和模糊推理的故障选相元件[J]. 电网技术, 2006, 30(14): 93-97.

Wang Xingguo, Zhang Ju. A novel faulty phase selector based on correlation analysis and fuzzy reasoning[J]. Power System Technology, 2006, 30(14): 93-97.

[19] 牛云涛, 李华, 宋志宏, 等. 谐振接地系统多判据多周期信息融合故障选线方法[J]. 电工技术学报, 2015, 30(增1): 512-517.

Niu Yuntao, Li Hua, Song Zhihong, et al. Fault line selection for grounding power network in arc suppression coil based on information fusion[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 512-517.

[20] 薛永端, 冯祖仁, 徐丙垠. 中性点非直接接地电网单相接地故障暂态特性分析[J]. 西安交通大学学报, 2004, 38(2): 195-199.

Xue Yongduan, Feng Zhuren, Xu Bingyin. Analysis of transient characteristics of signals phase earth fault in non-solidly earthed network[J]. Journal of Xi’an Jiaotong University, 2004, 38(2): 195-199.

[21] 薛永端, 李娟, 徐丙垠. 中性点经消弧线圈接地系统小电流接地故障暂态等值电路及暂态分析[J]. 中国电机工程学报, 2015, 35(22): 5703-5714.

Xue Yongduan, Li Juan, Xu Bingyin. Transient equivalent circuit and transient analysis of single- phase earth fault in arc suppression coil grounded system[J]. Proceedings of the CSEE, 2015, 35(22): 5703-5714.

A Method of Fault Line Selection in Resonant Earthed System Based on Zero Sequence Impedance Characteristic of Lines

（School of Electrical and Information Engineering Hunan University Changsha 410082 China）

After the single phase ground fault occurred in the resonant ground distribution network, the zero sequence impedance of the sound line shows capacitance characteristic under the circumstance that the frequency is below the minimum series resonant frequency. However, the zero sequence impedance of the faulty line presents capacitance characteristic in the high frequency and inductance characteristic in the low frequency. In terms of the phenomena above, a faulty line selection method based on zero sequence impedance characteristics of lines is proposed. The high and low frequency components of the bus zero sequence voltage and each feeder zero sequence current are extracted through low-pass and band-pass digital filters. And then the high and low frequency components of the bus zero sequence voltage are derived separately. Since the ratio between the voltage derivative and the current in the capacitive circuit is constant, the ratios between the bus zero sequence voltage derivative and the zero current of the sound line are same both in the high and the low frequencies theoretically. The actual difference of these two ratios is almost zero. Whereas, the ratios between the bus zero sequence voltage derivative and the zero current of the faulty line are different both in the high and the low frequencies, and the difference is greater. Therefore, a faulty line selection criterion is proposed. The method is proved to be accurate, reliable and adaptable through the theory and simulations.

Resonant earthed system, faulty line selection, feeder, single-phase grounding, zero sequence impedance

TM76

汤 涛 男，1989年生，博士研究生，研究方向为电力系统保护与控制。

E-mail: ttqzh0102@163.com

黄 纯 男，1966年生，教授，博士生导师，研究方向为电力系统继电保护、数字信号处理等。

E-mail: yellowpure@21cn.com（通信作者）

2015-11-30 改稿日期 2016-04-18

国家自然科学基金资助项目（51677060）。