模块化多电平变流器调速系统变频控制

殷 实 谭国俊 方 磊 曹晓冬



模块化多电平变流器调速系统变频控制

殷 实 谭国俊 方 磊 曹晓冬

（中国矿业大学信息与电气工程学院 徐州 221116）

模块化多电平变流器（MMC）凭借着诸多优势成为高电压大功率工况下的核心拓扑。但MMC变频调速系统运行于低频状态时存在桥臂能量分配不均衡、子模块电容电压波动严重等问题，不仅影响变频器全速域运行能力，甚至威胁系统安全。为解决上述问题，提出一种基于共模电压与偏置电压控制的MMC变频调速系统全速域运行方法，旨在通过控制系统各桥臂瞬时功率以快速抑制子模块电压波动。首先，构建系统数学模型，分析悬浮电容电压波动影响因素；其次，设计变频调速系统的低频控制器与在线模式切换环节；最后，为验证所提控制策略的可行性和有效性，对其进行仿真和实验的对比分析。实验结果表明，所提控制策略能有效抑制MMC变流器子模块电压波动，完成不同频段平滑切换，降低系统损耗，改善系统输出品质，提升MMC系统安全运行能力。

模块化多电平变流器驱动系统 共模电压控制 偏置电压控制 模式切换 降低系统损耗

0 引言

模块化多电平变流器（Modular Multilevel Con- verters, MMC）作为一种新型多电平拓扑结构，凭借其共母线结构、高度模块化、输出品质高、谐波含量少、结构灵活、可自由延展等诸多优势，被广泛应用于中、高电压大功率直流输电、新能源并网、电能品质改善等诸多领域[1-7]。

随着对MMC系统研究的深入，不同调制策略、先进控制方法相继被提出[8-17]，将输出品质更高、结构更灵活的MMC应用于中、高电压大功率调速领域成为可能。区别于传统H桥级联拓扑结构，由于MMC数目庞大的子模块并不是由多抽头变压器独立供电，MMC运行于低频段时悬浮电容电压波动严重，电压平衡被破坏，各相上、下桥臂电流畸变率大，系统输出电压、电流品质较差，甚至中断系统安全运行。由于MMC在低频状态下存在种种问题，阻碍了其在电机驱动系统领域的发展。

文献[18]理论分析了MMC悬浮电容电压波动幅值的影响因素。文献[19]提出了一种注入高频共模电压与环流高频分量的控制（Injecting Common Voltage and Circuit Current Control, IVC4）方法，从而达到抑制低频电容电压波动的控制目标。但上述方法仅讨论了特定调制度、特定频率的控制方法，并不适用于实时变化的变频调速工况。文献[20,21]针对变调制度问题进行改进，引入离线查表法思想，实现不同调制度、不同频段的控制。上述方法中均通过控制高频环流分量从而达到抑制悬浮电容波动的目标，但由于环流高频控制分量的引入，致使系统环流幅值增大，开关应力升高。同时MMC环流高频分量控制器设计难度较高，高低频控制器理想控制参数均不同，在工程应用过程中可实现度较低。

为解决上述问题，本文提出一种基于方波共模电压与偏置电压匹配控制的MMC变频系统全速域运行方法（Injecting Common Voltage and Bias Voltage control strategy, IBCV2）。分析MMC不同状态下各桥臂瞬时功率的变化，在低频控制环节，引入共模电压与偏置电压控制自由度。解决MMC低频段电容电压波动、能量均衡问题，改善输出品质，增强系统低频状态下的可靠运行能力。同时降低控制器设计难度，提升控制器工程应用的可实现性，设计高低频控制模式切换环节，完成系统低频段与高频段的平滑过渡，实现变频调速系统的全速域高精度控制。最后，搭建MMC变频调速实验平台，通过仿真和实验验证所提控制策略的正确性与可实现性。

1 MMC定义及基本工作原理

模块化多电平变流器拓扑结构如图1所示，为三相、六桥臂对称结构。变流器各相分为上、下两个桥臂，均由数个半桥型子模块与桥臂电感串联构成。MMC的子模块为系统功率单元，桥臂电感则起到抑制相间环流、减小故障冲击的作用。

图1 模块化多电平变流器拓扑结构

变流器正常工作时，子模块有投入、旁路、切除三种工作状态。当子模块半桥结构上、下管同时关断时，子模块处于切除状态（即冗余热备用状态）。若上管导通、下管关断，子模块处于投入状态，sm=1；若上管关断、下管导通，子模块处于旁路状态，sm=0。参考MMC拓扑结构，基于基尔霍夫电流定律，各相上、下桥臂电流（i,p,i,n）可表示为

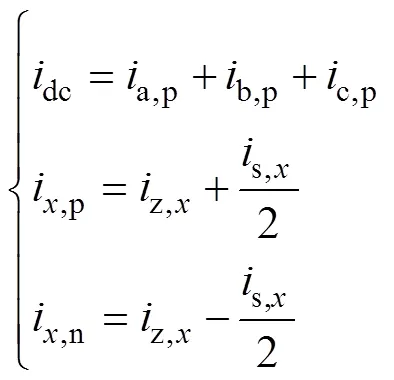
式中，=a,b,c分别表示变流器a、b、c三相；p、n分别表示上、下桥臂；dc为母线电流；z,x为各相环流；s,x为MMC交流侧电流。

由于环流存在于系统内部，不便直接测量，由式（1）可获得各相内部环流表达式为

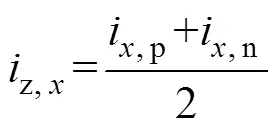
子模块电容电压与其所附属的桥臂电流p、n存在耦合关系，如式（3）所示。通过控制子模块的投、切状态，从而控制其电容能量交换过程，维持电容电压稳定。MMC正常工作时，为便于分析，可将系统各桥臂简化为可变电压源，则MMC简化电压模型如图2所示。各桥臂的子模块端口电压构成了桥臂电压v,y。

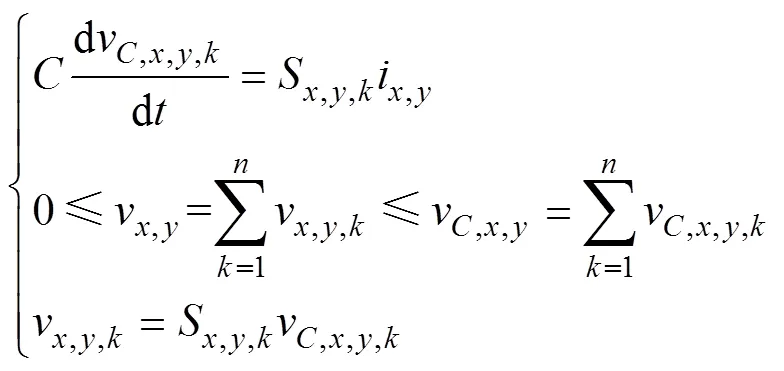
式中，v,y为各相上、下桥臂电压，=p,n；为子模块电容；=1,2,3,…,，为各桥臂1～号子模块；v,y,k为子模块输出电压；v,y,k为子模块电容电压；S,k为子模块投切状态。

图2 MMC简化电压模型

基于基尔霍夫电压定律，各相上、下桥臂电压与变流器交流侧电压及桥臂偏置电压关系为

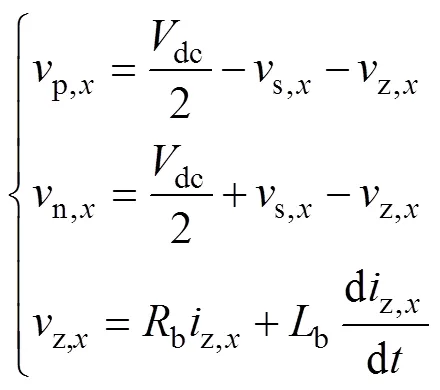
式中，dc为MMC直流母线电压；s,x为交流侧电压；z,x为桥臂偏置电压；b、b分别为桥臂电感的等效电感与电阻。

2 MMC低频状态分析

2.1 子模块电容电压波动问题

由于系统功率单元并不是理想直流源，其悬浮电容支撑子模块的输出电压，需通过周期性的能量交换维持电容电压稳定。子模块电容电压波动情况如图3所示，其波动系数可表示为[15]

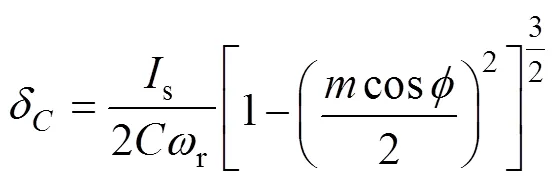
式中，s为变流器交流侧电流幅值；为MMC调制系数；r为变流器输出角速度；为输出功率角。

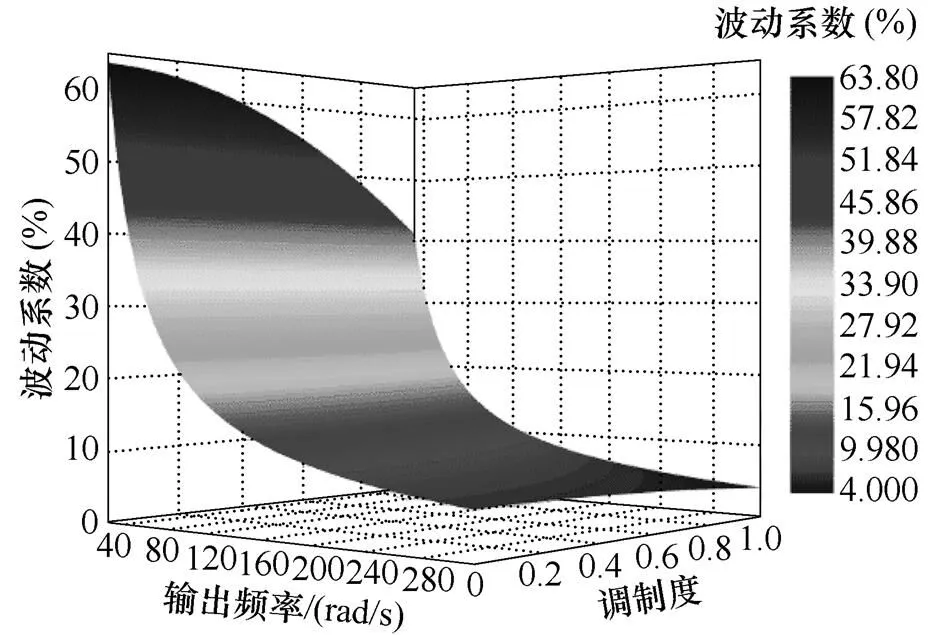
图3 子模块电容电压波动情况

由图3可知，若变流器系统处于低频状态时（即0＜converter＜12Hz，悬浮电容的波动十分严重。在输出频率相同的情况下，系统处于低调制度区域时，波动更为明显。若子模块的电压波动严重，不仅会侵占系统所需的有效调制区间，使得控制器无法完成既定的控制目标，输出电压品质变差，谐波含量升高，甚至会使稳定系统产生振荡，中断系统安全运行。

2.2 上、下桥臂能量均衡问题

参考式（1）、式（4），各相上、下桥臂的瞬时功率可表示为

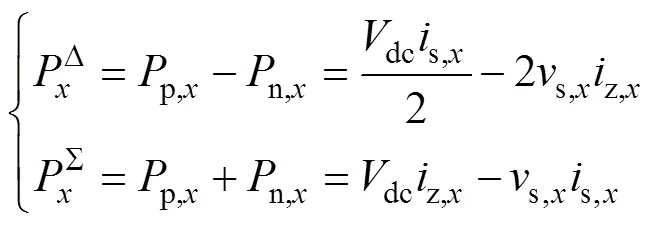
MMC运行于低频状态时，各相上、下桥臂功率偏差为低频分量且波动周期过长，致使上、下桥臂子模块所存储的总电能偏差累积放大，破坏子模块电容电压平衡。同时，系统各相的瞬时功率之和也为低频量，若长时间处于低频状态且不对其进行控制，子模块电容电压不仅产生较大的波动，同时会偏离功率单元期望电压。

3 MMC低频控制器设计

若想实现MMC变频调速系统高精度全速域运行，同时控制系统成本，需解决低频段存在的能量分配不均衡、悬浮电容电压波动等问题，因此在低频控制环节中需引入控制自由变量。控制自由变量只作用于变流器内部，对输出变量不产生影响。同时能够最大限度地消除桥臂瞬时功率偏差与各相总功率的低频分量，从而改善各桥臂能量交换过程，抑制子模块电容电压波动，提高系统输出品质，实现对MMC调速系统的高精度控制。

3.1 共模电压控制

高频共模电压注入MMC后，仅改变各相上、下桥臂电压与相电压，对系统输出线电压及电流并不产生影响。系统注入高频共模电压后，上、下桥臂功率变为

式中，com为MMC系统注入的共模电压。其表达式及标幺调制信号可表示为

式中，com为注入共模电压幅值；为注入共模电压角频率；为注入共模电压初始角；com为标幺共模电压调制信号；com为共模电压调制信号比，后文中均用该方法表述。

参考式（8），系统注入高频共模电压后，各相上、下桥臂瞬时功率偏差表达式为

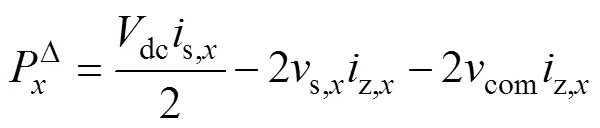
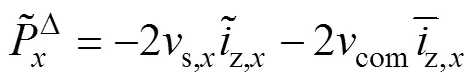
由式（11）可知，在匹配注入高频共模电压与同频率的环流后，可消除变流器在低频段所产生的低频偏差分量。同时，为避免MMC系统出现过调制现象，参考式（3），注入共模电压的幅值需满足

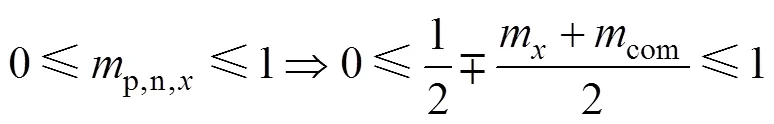
式中，p,n,x为变流器上、下桥臂的调制系统；m为交流侧输出调制系数。

在抑制MMC低频电容电压波动的过程中，由于需要高频环流的介入，致使系统开关应力上升。为此设计低频控制器时，为提高系统的可靠运行能力，需尽可能地减小各相环流的幅值，降低开关应力，减少系统损耗。

由式（11）可知，增大注入共模电压的幅值可降低控制系统所需环流高频控制分量的幅值。但在低频控制环节中，所注入共模电压幅值大小是受到调制区域硬性约束的。为最大可能地减小控制器所需高频环流分量，同时不占用调速控制系统所需的调制区域，在确保系统所注入共模电压幅值不变的情况下，提升注入共模电压基波幅值是降低系统损耗的有效解决方案。为此，可用方波共模电压控制信号替代正弦波，则注入共模电压可表示为

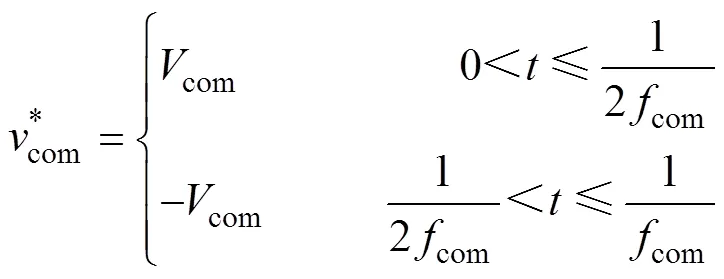
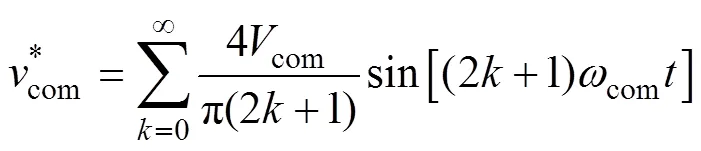
参考式（11）、式（15），系统低频控制所需的各相环流高频分量大小与注入共模电压基波成反比关系。将注入的方波共模电压替换传统控制策略所使用的正弦共模电压后，系统低频运行过程中所需环流高频分量降低了21%。

3.2 高频偏置电压控制

环流只存在于变流器内部，并不影响MMC系统输出电流，若其与系统所注入共模电压匹配控制即可消除偏差功率的低频分量。为实现对高频环流分量的控制，多采用比例谐振控制器（Proportional Resonant-Controller, PR-Controller），但PR-Controller的参数选取难度较大，可实现度较低。为简化控制架构，降低控制器设计难度，在低频控制器设计过程中，采用偏置电压控制方案。

参考式（4）可知，各相偏置电压高频分量与高频环流之间存在一阶线性关系。通过对各相偏置电压进行控制，即可获得理想的环流控制信号。为配合系统所注入的共模电压消除功率偏差低频分量，各相偏置电压高频控制分量可表示为

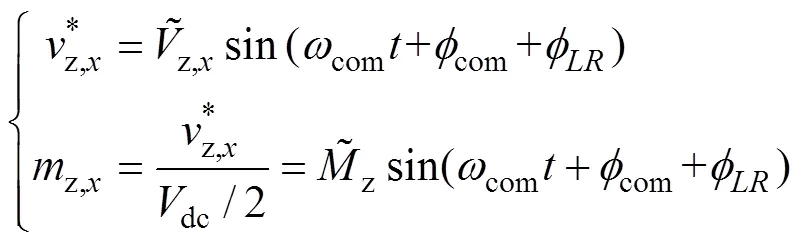
式中，z,x为各相偏置电压；为偏置电压高频分量幅值；为偏置电压初始角；为标幺偏置电压高频分量调制信号；为偏置电压高频分量调制比。

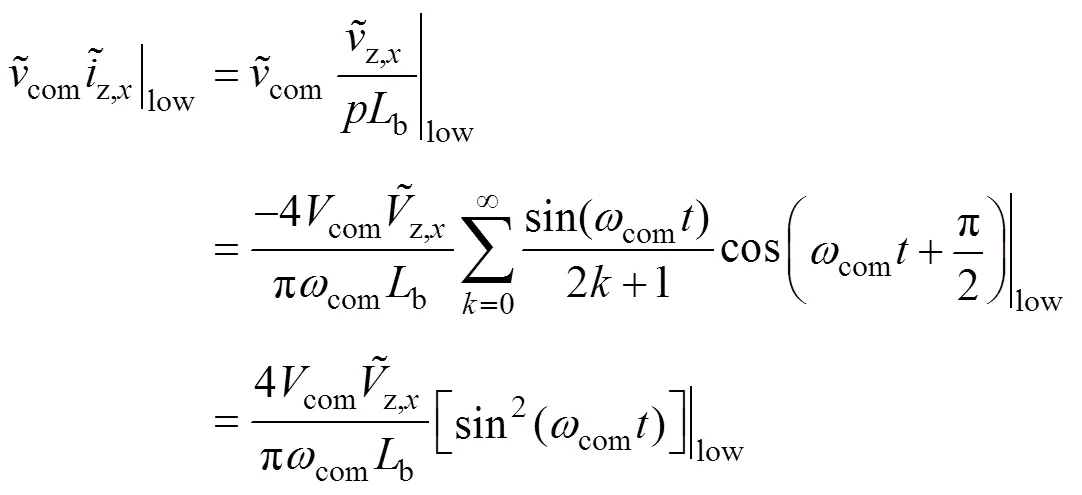
为实现MMC低频状态下桥臂功率均衡控制，需满足

将式（17）代入式（10）和式（18），整理可获得变流器系统桥臂偏置电压给定为

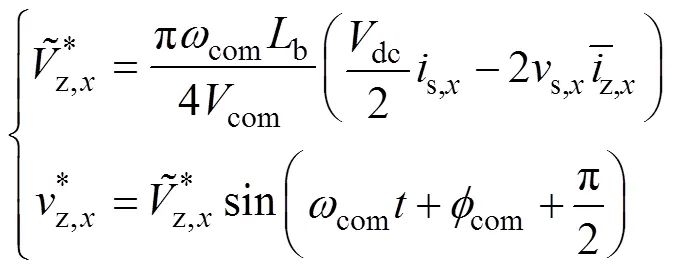
由注入方波共模电压的傅里叶级数展开式可知，共模电压信号中不仅含有频率为com的基波分量，同时包含(2+1)com的倍频分量。相比于仅引入频率为com偏置电压方法，在获得相同控制效果的前提下，同时引入倍频分量的方法能够有效地降低系统环流幅值。引入基波分量与三倍频分量后，所注入的偏置电压信号可表示为

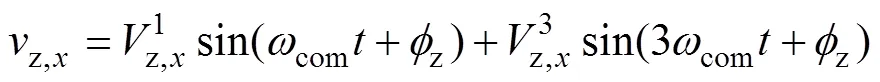
将式（20）代入式（10）、式（18）中，可得

式中，1、3分别为偏置电压基频分量与三倍频分量比例。

由式（4）可知，控制系统所注入的高频偏置电压幅值与相间环流高频分量幅值成正比。为降低系统开关应力，需尽可能地减小偏置电压，即

求解式（22）可获得1=0.9；3=0.3。则有

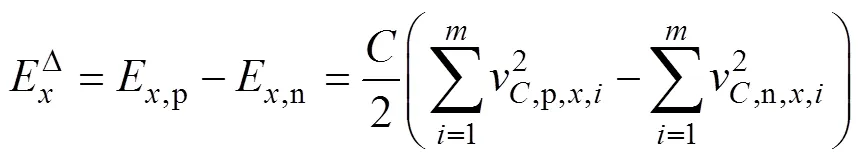
为最大程度抑制电容电压波动，确保各相上、下桥臂能量均衡，消除控制扰动，控制器设计过程中引入前馈思想。IBCV2策略偏置电压高频分量控制如图4所示，为消除存储电能偏差，给定设置为0。

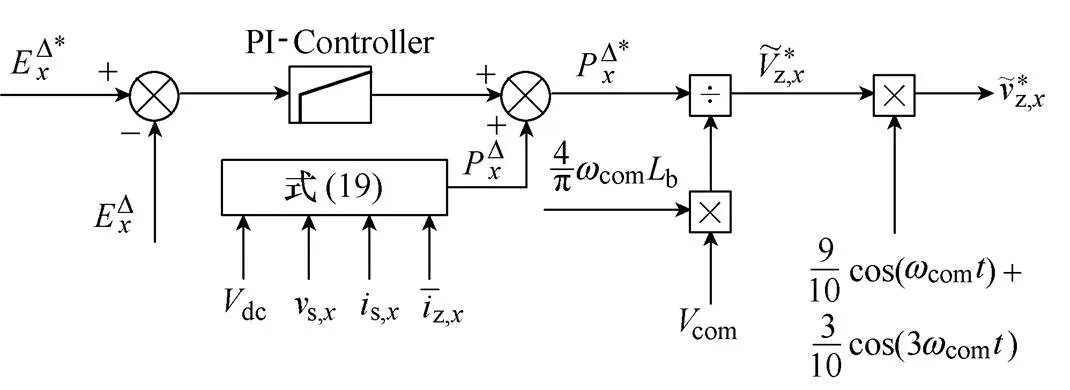
图4 IBCV2策略偏置电压高频分量控制

3.3 低频偏置电压控制

为使各个子模块电压跟踪期望电压，需确保对变流器交、直流侧能量交换情况，各相瞬时总功率进行控制。注入共模电压后，参考式（8），系统各相总功率可表示为

若子模块电容电压趋近恒定，在系统子模块期望给定上下小幅值波动，则需确保各相瞬时功率总

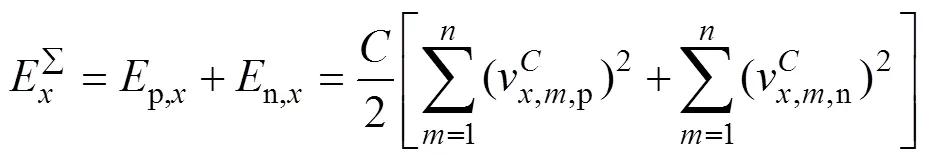
参考式（26），通过控制偏置电压低频分量，即可控制各相总功率恒定，维持电容电压在给定值（dc/）附近。为此设计低频偏置电压控制器，IBCV2策略偏置电压高频分量控制如图5所示。

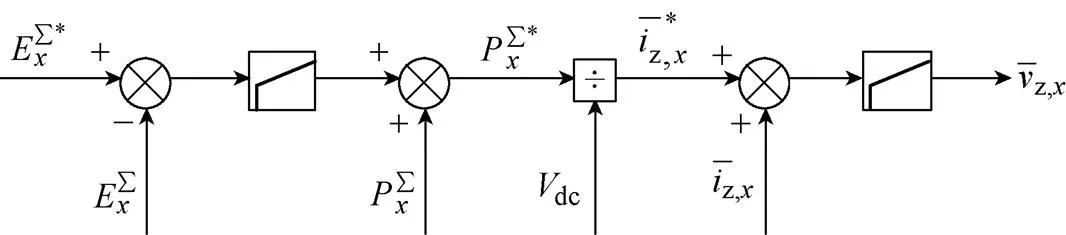
图5 IBCV2策略偏置电压高频分量控制

4 MMC高频控制

变流器系统运行于高频状态时，由式（7）可知，偏差功率的低频分量几乎为0，悬浮电容交换能量的速率加快，在协处理器中设计简单的子模块电压均衡方法，即可确保子模块电容电压在给定值附近小幅值波动。为此，在MMC变频调速系统运行于高频状态时，系统上、下桥臂调制信号中无需引入附加控制自由变量，即

在高频状态下，上、下桥臂电压之和与变流器直流母线之间仍存在电压偏差，且MMC仍有内部环流，为降低功率器件的开关应力，提升安全运行能力，需对环流进行抑制。高频控制器设计过程中，参考式（7），同样需对相功率进行控制。为此，系统运行于高频模式下时，控制器保留偏置电压低频分量控制，即

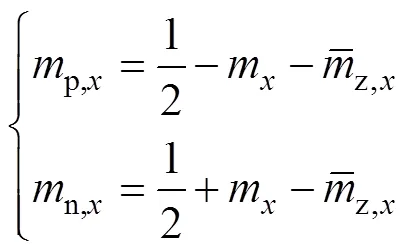
5 模式切换

IBCV2低频控制策略是MMC电容电压低频波动抑制的有效解决方案，但长时间在电压调制信号中注入共模电压、偏置电压信号后，会增大系统开关应力，占用调制区域。为此，MMC控制器设计过程中需要在系统损耗、调制区间和抑制电容电压波动等控制需求之间寻求一个平衡点。同时电机起动、制动、运行是一个动态变频过程，需参考系统输出需求，共模电压、偏置电压何时注入，偏置电压给定的高、低频分量的选取，控制分量的大小都是模式切换环节所需解决的问题。

在MMC控制器模式切换环节中引入模糊决策理论，其原理如图6所示。以系统输出频率为评价

图6 模糊决策原理

准则，将频率0～50Hz及以上区间分为约束控制段1、线性控制段2与最优控制段3。针对不同频段的控制指标，在线修正共模电压与偏置电压的控制信号，实现MMC变频器的全速域运行。MMC变频驱动系统模式切换环节的线性决策函数为

式中，f为变流器输出频率；high、low分别为模式切换环节的高、低频控制阈值。由此可得

（1）若f＜low，模式切换环节则判定系统处于约束控制段。为使系统安全稳定运行，确保上、下桥臂能量平衡，最大限度地降低悬浮电容的波动，需注入满幅值的共模电压与偏置电压高频控制分量，即com=1=1，从而维持系统安全稳定运转。为此，抑制电压波动为约束控制段的最高优先级控制目标。

（2）若f＞high，则控制器判定系统运行于最优控制段，变流器输出频率较高，各桥臂之间能量交换快，可自然均衡。悬浮电容电压波动较小，无需共模电压和偏置电压高频控制信号，仅协处理器就均压问题进行处理，此时com=3=0。在最优控制段，电容电压是否跟随给定、环流大小的抑制情况的好坏则是评判控制效果的首要准则。

（3）若low≤f≤high，则系统运行于线性控制段，变流器需在电容电压波动与调制区间大小、开关损耗之间寻求平衡。随着变流器输出频率逐渐升高，系统对电容电压波动抑制的控制需求逐渐减弱，模式切换环节也需将控制分量不间断地在线修正，如式（30）所示，。

引入模式切换环节后，共模电压与偏置电压的调制信号表示为

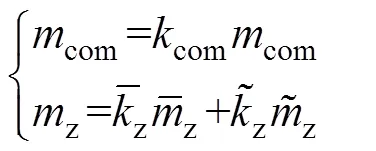
6 仿真

为验证所提策略的控制性能，在Matlab/ Simulink环境下，搭建MMC变频调速系统仿真模型，对不同控制方法进行仿真对比。MMC变频调速系统控制框图如图7所示，MMC及电机仿真参数见表1、表2。

图8为MMC变频调速仿真波形，MMC变频调速系统未引入低频控制策略模型（Control Strategy without Low-frequency Mode, CSLM）和采用IBCV2策略的电机起动过程对比实验波形如图8a所示。若MMC电机驱动系统控制器仅采用传统变频器的控制策略，未设计独立低频控制环节，低频状态下子模块电容电压波动明显，且持续时间较长，变流器输出线电压、电流畸变率较大。由图8可知，传统MMC控制方法无法解决其在低频段所存在的问题，不仅影响输出品质，同时威胁着系统安全。若控制系统采用IBCV2策略，其仿真波形如图8b所示，由于控制自由变量的引入，对系统低频段瞬时功率进行控制，子模块电容电压波动得到明显抑制，波动幅值大大降低，变流器系统输出品质得到明显改善，电机起动过程转速上升平滑。IBCV2策略的引入不仅增强了系统高精度控制、全速域运行能力，同时降低了损耗，确保系统在不同工况下的稳定运行。

图7 MMC变频调速系统控制框图

表1 MMC仿真参数

Tab.1 Simulation parameters of MMC system

表2 电机仿真参数

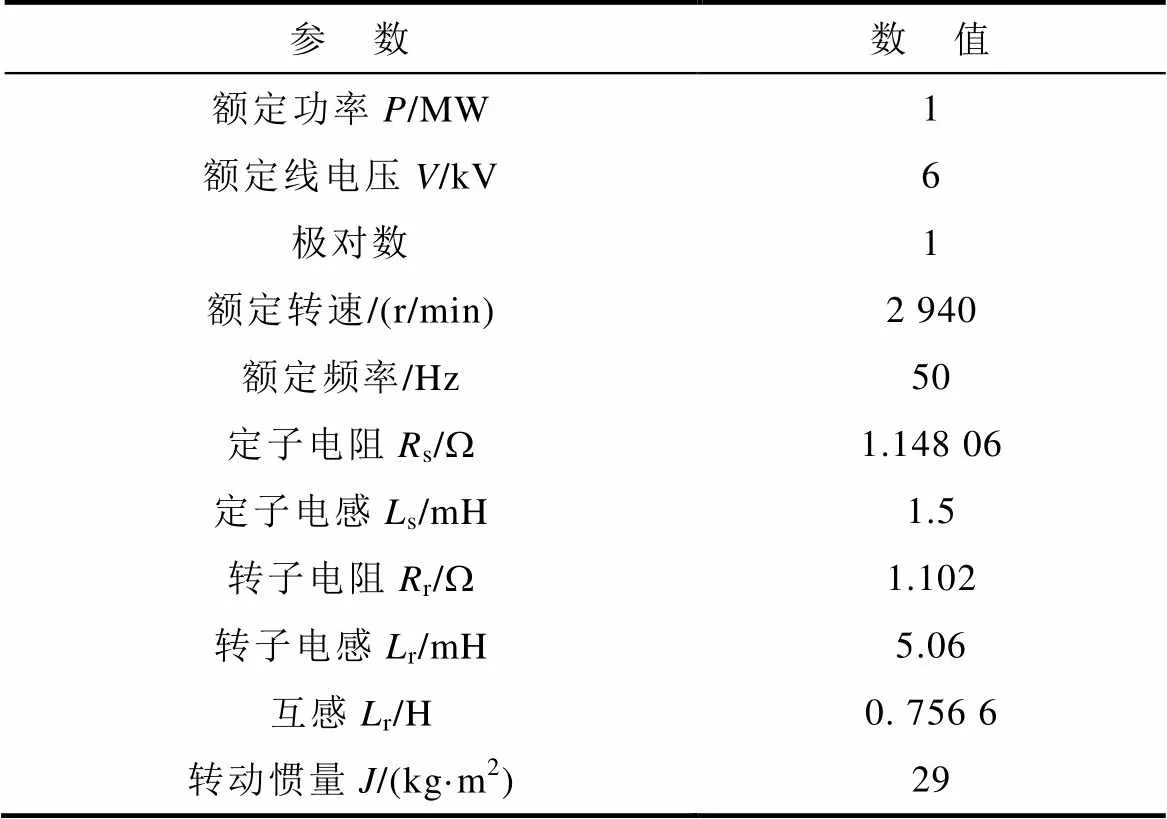
Tab.2 Simulation parameters of motor system

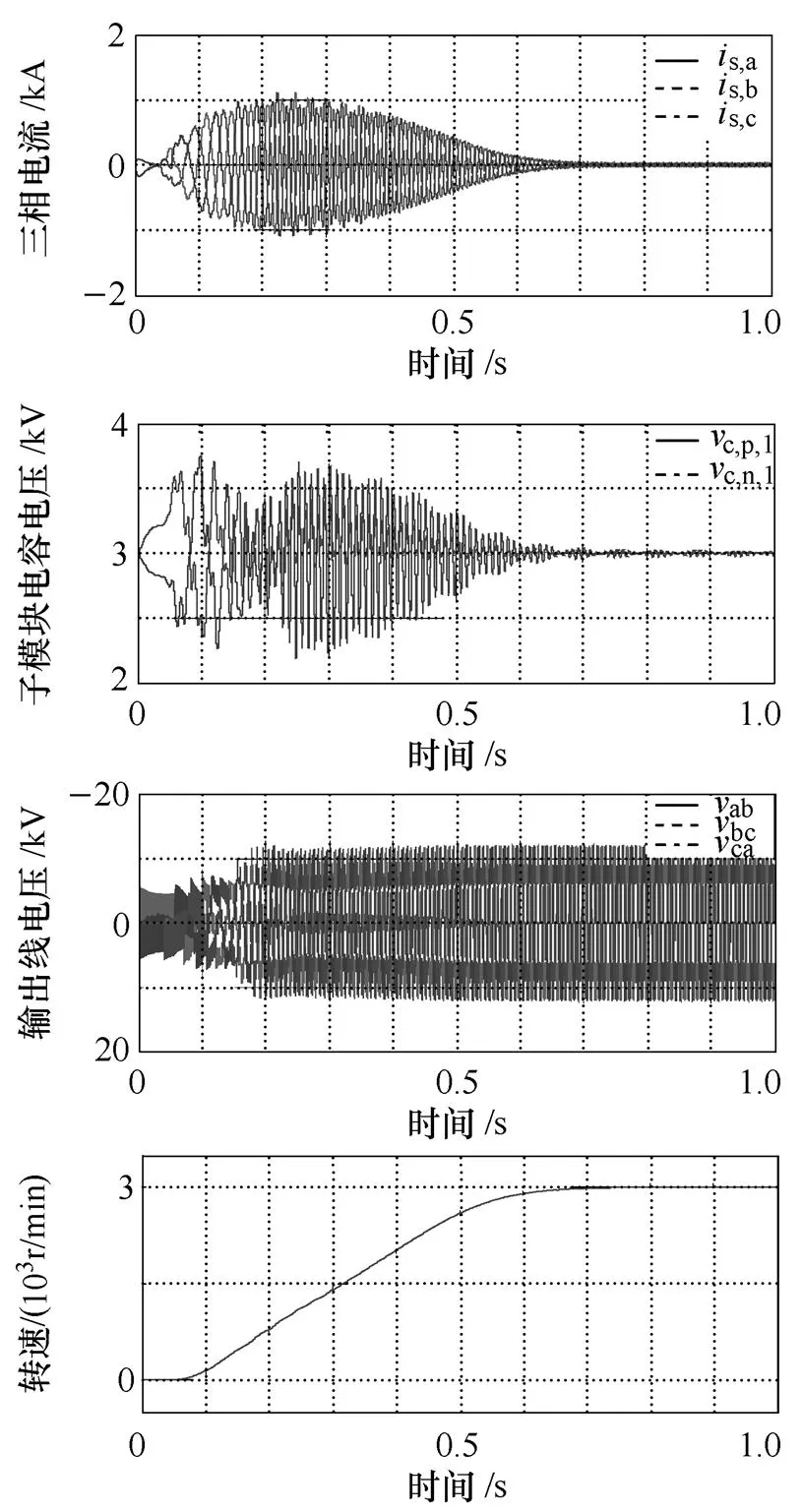
（a）未引入低频控制策略

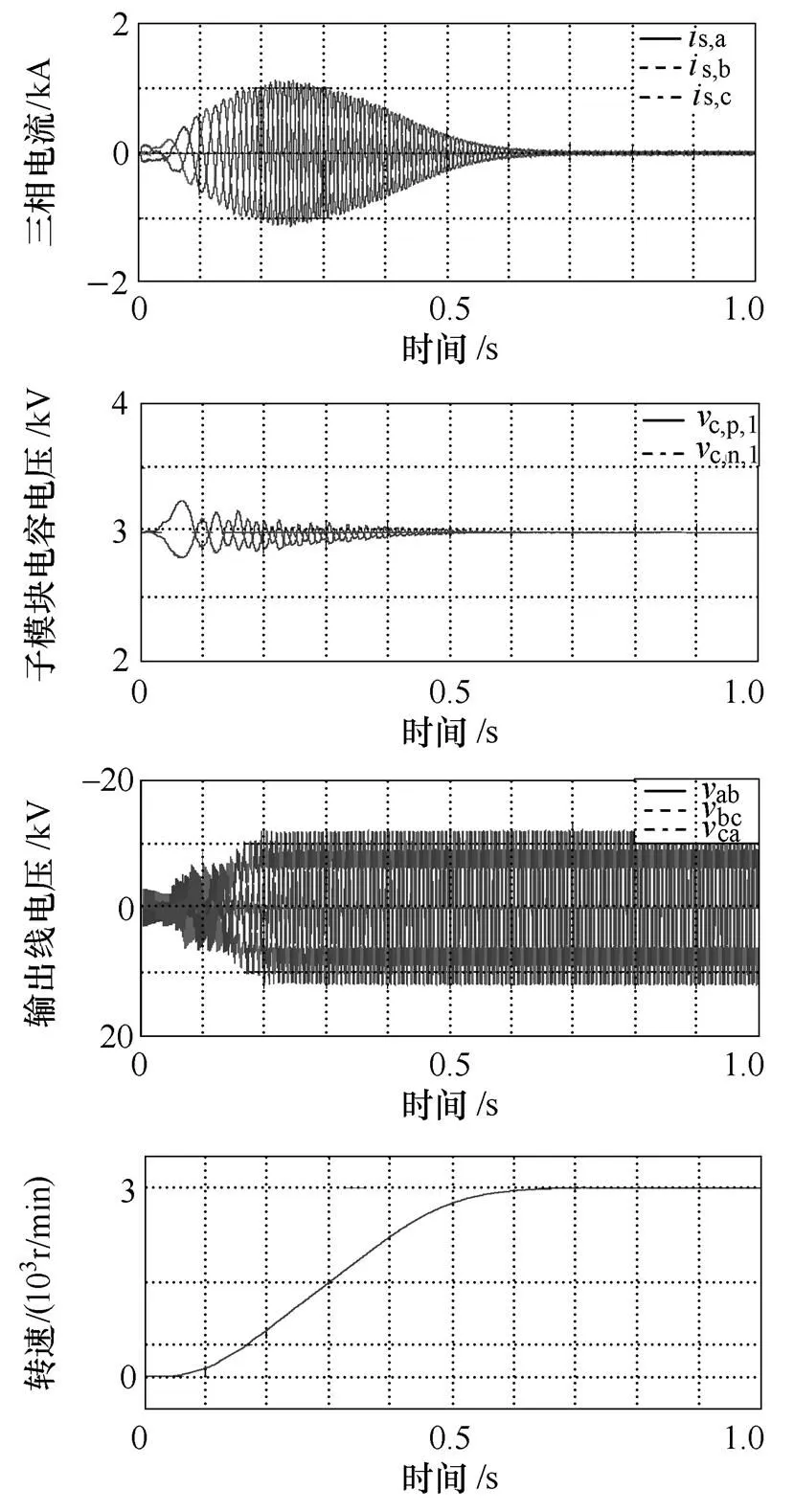
（b）IBCV2控制策略

图8 MMC变频调速仿真波形

Fig.8 Simulation waveforms of MMC drive system

7 实验

为进一步验证所提MMC调速系统变频控制策略的有效性与可实现性，搭建三相MMC调速系统实验样机如图9所示。由于实验条件所限，MMC直流母线电压为500V，子模块电容为2 200mF，桥臂电感为1.5mH。核心控制器采用DSP+FPGA数字处理系统架构，DSP28335芯片完成核心算法，FPGA3S500E作为协处理器完成AD采样、死区保护等辅助功能，系统控制器结构如图7所示。IGBT采用英飞凌公司的FF400R12KT3，为方便测量，将需观测的输出线电压、电流、子模块电容电压等变量经D-A转换并用安捷伦MSO6014A示波器观测。

图9 MMC调速系统实验样机

7.1 对比实验

图10为MMC驱动系统低频状态对比实验波形。图10a～图10c分别为未引入低频控制策略与IVC4策略和IBCV2策略在系统处于输出频率10Hz、25%负载转矩情况下，变流器三相输出电流、上下桥臂电流和子模块电容电压对比实验波形。由图10可知，传统IVC4策略与IBCV2策略均能有效地抑制子模块低频电容电压波动，变流器输出电流三相对称且正弦度良好，低频控制方案的引入，不仅提升了MMC的可靠性，同时优化了变流器的输出品质。但相比较于传统IVC4策略，在注入共模电压幅值相同的情况下，由于方波共模电压与倍频偏置电压的引入，系统上、下桥臂电流幅值降低了30%。在确保变流器获得较好的控制效果的前提下，降低了功率器件的开关应力与损耗，提升了系统的稳定运行能力。

表3给出了三种控制方法性能对比概述，其内容包括子模块电容电压波动系数、输出电流畸变率、算法复杂度、模型依赖度和开关应力大小。从表3中对比结果可以看出，未引入低频控制环节的传统控制策略作为算法复杂程度最低的方案，运行于低频状态下时，电容电压波动情况严重，输出品质较差，更适用于工频工况如电能传输工程等。IVC4策略引入低频控制环节，有效地抑制了子模块电容电压低频波动，系统低频输出品质得到改善，但控制器设计难度较大。IBCV2作为IVC4策略的改进方案，在降低系统开关应力的情况下，也可获得优异的控制精度，但是该方法相比于IVC4策略，系统参数依赖性略有上升，但简化了控制器的结构，提升了其在工程应用中的可实现性。

（a）未采取低频控制策略 （b）采用IC4V控制策略 （c）采用IBCV2控制策略

图10 MMC驱动系统低频状态对比实验波形

Fig.10 Contrast experimental waveforms of MMC drive system

表3 CSLM、IVC4、IBCV2三种控制方法性能对比

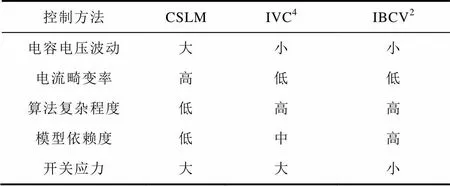
Tab.3 Comparative results among three control methods of CSLM, IVC4 and IBCV2

7.2 动态实验

为验证所提控制策略的动态性能，变频调速系统控制器能够实现在不同调制度、输出频率状态下的悬浮电容电压波动抑制与能量均衡，对基于IBCV2策略的MMC变频调速系统进行电机起动实验。变流器系统在变频调速过程，尤其运行于低频模式，IBCV2能有效地抑制电容电压波动。随着变流器系统输出频率的变换，IBCV2策略实时在线修正注入共模电压的幅值、偏置电压的控制量，完成变流器不同频段的平滑过渡，实现MMC的全速域运行。

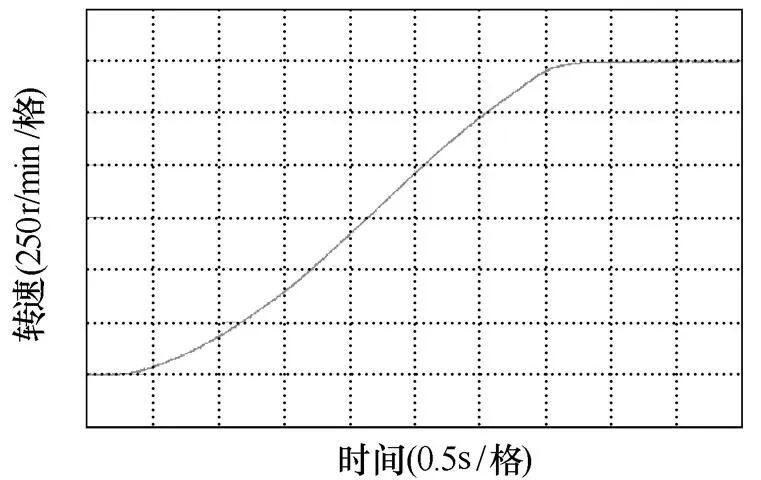
（a）电机起动转速波形

（b）三相电流波形

（c）a相上、下桥臂电流

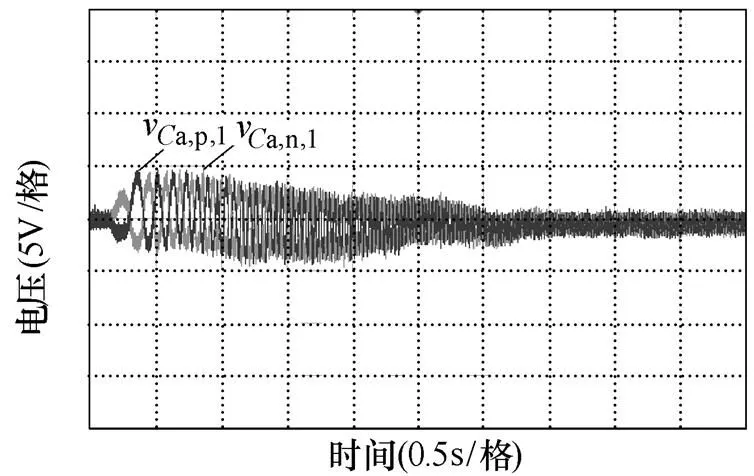
（d）a相上、下桥臂电容电压波形

图11 IBCV2策略动态实验

Fig.11 The dynamic experiments of IBCV2 strategy

8 结论

MMC运行于低频状态下时，电容电压波动严重，输出品质恶化。MMC变频驱动系统若实现全速域运行，亟需设计低频控制器，对悬浮电容电压、桥臂电流等系统内部状态变量进行控制，从而提升系统控制精度与可靠运行能力。本文以分析桥臂瞬时功率为基础，引入共模电压与偏置电压作为控制自由变量，消除MMC系统上、下桥臂功率偏差与各相总功率的低频分量，抑制悬浮电容的能量累积。同时在控制器模式切换环节中，引入模糊决策理论，在线修正控制分量，力求在系统损耗与控制精度之间寻求平衡点，完成高、中、低频控制的模式切换。仿真与实验结果表明，所提IBCV2策略能有效地解决不同频段下子模块电容电压波动问题，提升系统输出品质，同时减小桥臂电流，降低开关应力与系统损耗。无需设计环流比例谐振控制器，简化了控制架构，提升了控制策略的可实现性。IBCV2策略作为一种MMC变频调速系统的新型控制方法，为高电压大功率多电平变流器调速系统提供了新思路。

参考文献：

[1] Rodriguez J, Lai J, Peng F Z. Multilevel inverters: a survey of topologies, controls, and applications[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4): 724-738.

[2] Saeedifard M, Iravani R. Dynamic performance of a modular multilevel back-to-back HVDC system[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2903-2912.

[3] 彭浩, 邓焰, 王莹, 等. 模块化多电平变换器模型及稳态特性研究[J]. 电工技术学报, 2015, 30(12): 120-127.

Peng Hao, Deng Yan, Wang Ying, et al. Research about the model and steady-state performance for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 120-127.

[4] Zha X, Xiong L, Gong J, et al. Cascaded multilevel converter for medium-voltage motor drive capable of regenerating with part of cells[J]. IET Power Electronics, 2014, 7(5): 1313-1320.

[5] 楚遵方, 李耀华, 王平, 等. 柔性直流输电系统中模块化多电平变流器的直流侧充电策略分析[J]. 电工技术学报, 2015, 30(12): 136-142.

Chu Zunfang, Li Yaohua, Wang Ping, et al. Analysis of charging strategy by DC grid of modular multi- level converter in high voltage direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 136-142.

[6] Debnath S, Qin J, Bahrani B, et al. Operation, control, and applications of the modular multilevel converter: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 37-53.

[7] 邓雪松, 欧开健, 陈鹏, 等. 基于无差拍电流控制的MMC-HVDC系统控制策略研究[J]. 电力系统保护与控制, 2014, 42(8): 34-39.

Deng Xuesong, Ou Kaijian, Chen Peng, et al. Study of control strategy for MMC-HVDC system based on deadbeat current control[J]. Power System Protection and Control, 2014, 42(8): 34-39.

[8] 陆晶晶, 肖湘宁, 张剑, 等. 基于定有功电流限值控制的MMC型UPQC协调控制方法[J]. 电工技术学报, 2015, 30(3): 196-204.

Lu Jingjing, Xiao Xiangning, Zhang Jian, et al. MMC-UPQC coordinated control method based on fixed active current limit value control[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(3): 196-204.

[9] Mei J, Xiao B, Shen K, et al. Modular multilevel inverter with new modulation method and its application to photovoltaic grid-connected gener- ator[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5063-5073.

[10] 代高富, 赵丹, 林鹏峰, 等. 基于MMC拓扑的有源滤波器控制策略研究[J]. 电力系统保护与控制, 2015, 43(8): 74-80.

Dai Gaofu, Zhao Dan, Lin Pengfeng, et al. Study of control strategy for active power filter based on modular multilevel converter[J]. Power System Protection and Control, 2015, 43(8): 74-80.

[11] Konstantinou G, Ciobotaru M, Agelidis V. Selective harmonic elimination pulse-width modulation of modular multilevel converters[J]. IET Power Elec- tronics, 2013, 6(1): 96-107.

[12] Li B, Yang R, Xu D, et al. Analysis of the phase- shifted carrier modulation for modular multilevel converters[J]. IEEE Transactions on Power Electro- nics, 2015, 30(1): 297-310.

[13] Meshram P M, Borghate V B. A simplified nearest level control (NLC) voltage balancing method for modular multilevel converter (MMC)[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 450-462.

[14] Bergna G, Berne E, Egrot P, et al. An energy-based controller for HVDC modular multilevel converter in decoupled double synchronous reference frame for voltage oscillations reduction[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2360-2371.

[15] Zhang M, Huang L, Yao W, et al. Circulating harmonic current elimination of a CPS-PWM-based modular multilevel converter with a plug-in repetitive controller[J]. IEEE Transactions on Power Electro- nics, 2014, 29(4): 2083-2097.

[16] 李爽, 王志新, 吴杰. 采用基频零序分量注入的MMC换流器故障容错控制研究[J]. 电力系统保护与控制, 2014, 42(17): 1-7.

Li Shuang, Wang Zhixin, Wu Jie. Study on fault-tolerant operation control strategy of modular multilevel converters injected with fundamental- frequency zero-sequence voltage component[J]. Power System Protection and Control, 2014, 42(17): 1-7.

[17] 陈耀军, 陈柏超, 袁佳歆, 等. 模块化多电平逆变器电容电压及环流控制[J]. 电工技术学报, 2014, 29(10): 166-174.

Chen Yaojun, Chen Baichao, Yuan Jiaxin, et al. The control of capacitor voltages and circulating currents of the modular multilevel inverter[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 166- 174.

[18] 周月宾, 江道灼, 郭捷, 等. 模块化多电平换流器子模块电容电压波动与内部环流分析[J]. 中国电机工程学报, 2012, 32(24): 8-14.

Zhou Yuebin, Jiang Daozhuo, Guo Jie, et al. Analysis of sub-module capacitor voltage ripples and circula- ting currents in modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(24): 8-14.

[19] Korn A J, Winkelnkemper M, Steimer P. Low output frequency operation of the modular multi-level converter[C]//IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, USA, 2010: 3993-3997.

[20] Antonopoulos A, Ängquist, Lennart, et al. Modular multilevel converter ac motor drives with constant torque from zero to nominal speed[C]//IEEE Energy Conversion Congress and Exposition (ECCE), North Carolina, USA, 2012: 739-746.

[21] Debnath S, Saeedifard M. Optimal control of modular multilevel converters for low-speed operation of motor drives[C]//Twenty-Ninth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Pennsylvania, USA, 2014: 247-254.

Variable-Frequency Control Strategy of Modular Multilevel Converter

（School of Informationand Electrical Engineering China University of Mining and Technology Xuzhou 221116 China）

With the advantages of modularization, flexible structure and convenient expansion, modular multi-level converters (MMC) become the core topology under the condition of high voltage and high power. In low frequency status, the problems, such as unbalanced energy distribution in arms, severe pulsation of sub-module capacitor voltage in MMC variable-speed drives system, will exist. These problems will not only affect the running ability of full speed area, but threaten the system safety. Therefore, a full speed area running method based on common voltage and bias voltage control for MMC variable-speed drives system is proposed. The proposed method can suppress the pulsation of sub-module capacitor voltage by controlling instantaneous power of each arm. Firstly, the mathematical model of MMC system was built to analyze the influencing factors for pulsation of sub-module in low-frequency. Then, the low frequency controller and on-line link of mode switch were designed for variable-speed drives system. Last, the comparisons of the simulations and experiments verified the proposed control strategy. The results show that the control strategy proposed can effectively suppress the pulsation of MMC sub-module capacitor voltage, accomplish smooth switch during different frequencies, reduce system loss, and hence improve the system output quality and the safety performance of MMC system.

Modular multi-level converters drive system, common voltage control, bias voltage control, mode switch, reduce system loss

TM921.51

殷 实 男，1990年生，博士研究生，研究方向为多电平变流器控制方法等。

E-mail: yinshicumt@163.com（通信作者）

谭国俊 男，1962年生，教授，博士生导师，研究方向为电力电子与电力传统等。

E-mail: gjtan@cumt.edu.cn

2015-12-30 改稿日期 2016-05-20

江苏省研究生培养创新工程（KYLX_1380）和江苏省自然科学基金（BK20140204）资助项目。