结合开关表的三电平逆变器永磁同步电机模型预测转矩控制
2016-11-17夏长亮张天一周湛清张国政史婷娜
夏长亮 张天一 周湛清 张国政 史婷娜
结合开关表的三电平逆变器永磁同步电机模型预测转矩控制
夏长亮1,2张天一1周湛清1张国政1史婷娜1
(1. 天津大学电气与自动化工程学院 天津 3000722. 天津市电机系统先进设计与智能控制技术工程中心 天津 300387)
提出了一种应用于中点钳位型(NPC)三电平逆变器馈电的永磁同步电机(PMSM)调速系统的改进模型预测转矩控制(MPTC)策略。该策略将评价函数中磁链和电磁转矩控制部分等效为空间矢量图中参考电压与基本电压矢量差的模,然后合理划分区域,建立能够选择出使上述模最小的电压矢量的预测开关表。并将这个电压矢量作为第二步预测的输出,从而以一次查表代替传统MPTC第二步预测中多次模型预测计算。实验结果证明,改进策略可以很好地实现对磁链、电磁转矩和中点电位的控制的同时,解决了传统两步预测MPTC计算量大的问题。
中点钳位型三电平逆变器 永磁同步电机 模型预测转矩控制 预测开关表
0 引言
直接转矩控制(Direct Torque Control,DTC)作为一种高性能电机调速方案,已经延伸到多电平逆变器领域,成为工业和学术界重要的研究课 题[1,2]。多电平逆变器主要面向中、高电压场合,其中,中点钳位型(Neutral Point Clamped,NPC)三电平逆变器的应用最为广泛[3,4]。
当DTC应用于NPC三电平逆变器驱动的电机调速系统时,在利用电压矢量控制电机磁链和电磁转矩的同时,还应该满足NPC三电平逆变器的以下运行要求:①相邻电压矢量切换过程中,相电压和线电压的跳变幅值不应该超过直流母线电压的一半;②保持中点电位平衡[5,6]。基于单一电压矢量的DTC控制策略,按照磁链和电磁转矩的控制要求选择基本电压矢量,如果被选电压矢量不满足电压矢量切换或中点电位平衡的要求,先插入满足要求的电压矢量,然后再过渡到被选电压矢量[5]。文献[7,8]优化了控制磁链和电磁转矩的电压选择方案,但仍采用插入过渡电压矢量的方法来满足逆变器运行要求。由于过渡电压矢量对磁链和电磁转矩的作用,并不总满足控制要求,因而导致控制性能并不理想。文献[9-11]采用合成虚拟电压矢量作为磁链和电磁转矩控制矢量,在虚拟电压矢量合成过程中兼顾了电压矢量切换和中点电位平衡的要求,但是使用合成矢量不可避免降低了电压利用率。
为了合理、有效地利用逆变器产生的基本电压矢量,可以采用模型预测转矩控制(Model Predictive Torque Control,MPTC)。MPTC能够很好地将逆变器产生的基本电压矢量和控制目标结合在一起,它易于处理系统的约束,并能够实现对多个变量的控制[12-14]。当MPTC应用于由NPC三电平逆变器驱动的电机调速系统时,只需根据电压矢量切换要求调整有限控制集,同时预测中点电位,并在评价函数中添加中点电位控制目标项,即可满足NPC三电平逆变器的运行要求[15,16]。为了选择更合理的输出电压矢量,MPTC预测过程需要考虑过渡电压矢量对电机状态的影响,因此,多步预测MPTC更适合NPC三电平逆变器驱动的电机调速系统。此外,采用多步预测算法可以获得更好的稳态性能。
然而随着预测步数的增加,MPTC算法的计算量会呈指数倍增加,这在一定程度上限制了MPTC的应用。相关文献通过对算法进行优化来减小计算量,其中,对两步预测MPTC的研究最为常见。文献[17]在第一步预测后只保留最优和次优开关状态,在此基础上进行第二步预测,来减少预测计算次数。文献[18]提出基于两电平逆变器的优化算法,首先计算无差拍电压矢量,然后根据其位置缩小有限控制集范围,从而减小算法计算量。
本文针对NPC三电平逆变器驱动的永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)调速系统,提出一种两步预测MPTC改进策略,将MPTC与预测开关表相结合减小两步预测MPTC的计算量。首先分析NPC三电平逆变器电压矢量切换要求对MPTC控制性能的影响。然后解析评价函数中磁链和电磁转矩控制项在空间矢量图中的物理意义,通过物理关系建立可直接选出最优基本电压矢量的预测开关表,并将其应用到MPTC第二步预测中简化预测过程。最后,为了验证改进策略的正确性与控制的有效性,进行实验分析。
1 传统MPTC策略
1.1 NPC三电平逆变器
NPC三电平逆变器驱动PMSM拓扑结构如图1所示。逆变器每相可以输出三种电压分别为dc/2、0和-dc/2,分别对应输出状态P、O和N,dc代表直流母线电压。NPC三电平逆变器共有27个输出状态,对应19个不同的空间电压矢量,NPC三电平逆变器空间矢量如图2所示。按矢量幅值大小可以分为大矢量、中矢量、小矢量和零矢量。每个大、中矢量有一个输出状态,每个小矢量有两个输出状态,零矢量有三个输出状态。

图1 NPC三电平逆变器驱动PMSM拓扑结构
MPTC以逆变器产生的19个基本电压矢量作为有限控制集元素。NPC三电平逆变器运行时,相邻电压矢量切换过程中,相电压和线电压的幅值跳变都不超过dc/2。因此,MPTC有限控制集与上一采样时刻作用的电压矢量有关,两者关系见表1。

图2 NPC三电平逆变器空间矢量
表1 MPTC有限控制集元素

Tab.1 Elements of MPTC finite-control-set
MPTC利用基本电压矢量控制磁链和电磁转矩的增减,使磁链和电磁转矩快速地跟踪参考值。以定子磁链矢量s的位置作为参考将空间矢量图分为4个区域,电压矢量区域如图3所示。每个区域内的电压矢量对磁链和电磁转矩的作用不同[19]。为了满足NPC三电平逆变器的运行要求,不同区域之间的电压矢量可能不能直接切换,需要通过中间电压矢量过渡。而过渡电压矢量的作用结果往往与磁链、电磁转矩的控制要求是相反的。例如图3中,当前时刻输出令磁链和电磁转矩增加的电压矢量后,下一步要减小磁链或者电磁转矩,而过渡矢量的作用却会导致磁链和电磁转矩进一步增加,从而使控制性能下降。考虑上述因素以及系统扰动和建模误差的影响,当MPTC应用于由NPC三电平逆变器驱动的电机调速系统时,采用两步或多步预测算法更为合理,考虑到计算量,一般采用两步预测算法。

图3 电压矢量区域
由于流过NPC三电平逆变器直流母线中点的电流O不一定为零,中点电位O会发生偏移[5,11]。O与直流侧电容、逆变器输出状态和三相电流关系为[15]

式中,abc=[abc]T,a、b和c为三相电流;=;S为相开关状态函数,S∈{1, 0,-1},∈{a, b, c},1、0、-1分别代表状态P、O、N;为直流侧电容。
1.2 两步预测MPTC
建立dq旋转坐标系,将转子磁链定向到d轴,如图3所示。采用前向欧拉离散法对PMSM电机方程离散化,得到其预测模型为[20]

其中
式中,上标表示第s采样时刻;s为定子电流矢量,s=[dq]T;s为定子电压矢量,s=[dq]T;s为定子电阻(W);f为永磁体磁链(Wb);r为转子磁链角速度(rad/s);d、q分别为d轴和q轴电感(H);s为采样周期(s)。第(+1)s时刻的磁链和电磁转矩分别为


式中,为电机极对数。
将式(1)离散化,得到NPC三电平逆变器中点电位O的预测模型为

传统两步预测MPTC控制结构如图4所示,算法的主要步骤描述如下:
(1)延迟补偿。由于实际数字控制系统存在一步延迟,在s时刻选择输出的电压矢量会延迟到(+1)s时刻才被更新输出。为消除一步延迟的影响,采用提前预测一步的方式对延迟进行补偿[21]。具体措施为按式(2)和式(5)预测和,然后以和作为两步预测MPTC算法初值。

图4 传统两步预测MPTC控制结构
(3)第二步预测。由中第个元素()可确定第二步预测的有限控制集N,N为()对应的有限控制集,可以得到个集合。记N内的元素为(),其中=1,…,n,n为N中元素的数量。将这个有限控制集内的元素()以及第一步预测得到的中间变量s+2()依次代入到式(2)~式(5),计算(+3)s时刻的控制变量+3()。
(4)上述计算完成后得到如图5所示传统MPTC预测轨迹,每条轨迹代表(+2)s和(+3)s两时刻的磁链、电磁转矩和中点电位,将每条轨迹对应的两个时刻的预测值代入到评价函数中,即

式中,和O分别为电磁转矩和中点电位权重系数。选取使评价函数最小的预测轨迹,并将这条轨迹对应的(+1)s时刻的电压矢量作为输出。
从图5中可以看出,第二步预测要对个有限控制集N内所有元素执行模型预测计算。从表1可以看出,有限控制集元素数量为4、5或7。这意味着传统MPTC第二步预测最多要进行49次模型预测计算,计算量很大。较大的计算负担会导致采样周期增加,而这会抵消预测步数增加带来的控制性能的提升[15]。

图5 传统MPTC预测轨迹
2 改进MPTC策略
本文提出了一种计算更简单的改进MPTC策略。改进MPTC控制结构如图6所示。图6中,在第二步预测时,通过预测开关表从每个有限控制集N中,直接选择出最优矢量,作为(+2)s时刻的输出电压矢量。下面将介绍预测开关表的建立过程,以及改进MPTC的算法流程。

图6 改进MPTC控制结构
2.1 预测开关表的建立
传统MPTC的评价函数描述的是磁链和电磁转矩的参考值与实际值之间的关系。本文提出的改进MPTC在第二步预测时,将磁链和电磁转矩的参考值与实际值之间的关系变换为参考电压与实际电压之间的关系,从而得到评价函数中磁链项和电磁转矩项在空间矢量图中的物理意义,然后根据物理关系离线建立了预测开关表。
建立旋转坐标系,将定子磁链定向到轴,如图3所示。忽略定子电阻,则磁链和电磁转矩的变化率可以表示为

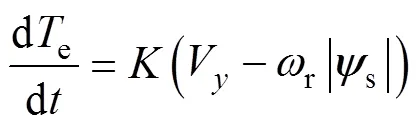
其中

式中,V和V分别为定子电压轴和轴分量(V);为定子磁链和转子磁链之间的夹角(rad)。将式(7)和式(8)离散化,可以得到


假定在(+3)s时刻,在参考电压r作用下,磁链和电磁转矩均达到参考值,即,,则有


式中,rx和ry代表参考电压r的、轴分量。
由式(10)~式(13)可得


记第二步预测时,传统评价函数式(6)中表示磁链和电磁转矩的控制部分为

将式(14)和式(15)代入式(16)中,并令=1/2,可得

在上述推导过程中,为电磁转矩权重系数。从式(9)可以看出,与|s|和有关。值随系统运行状态变化而变化。考虑到电机正常运行时,的变化范围较小,因此,在计算过程中取固定值,的整定将在2.3节分析。式(17)等号右边方括号内的式子在空间矢量图中的物理意义为|r-|2,即的大小与|r-|的长短是等价的。那么选择使最小的电压矢量即转化为选择使|r-|最短的电压矢量。
以r位于第一扇区为例,第一扇区区域划分如图7所示。第一扇区内基本电压矢量之间连线(图7中虚线)的中垂线,将第一扇区划分五个区域。若上一个采样周期作用电压矢量为1,r位于1号区域,那么第二步预测的有限控制集为{1,2,12,13}。根据r和中垂线1、2和3的位置关系,通过中垂线定理,可以判断|r-1|是最短的,即在有限控制集中1对应的最小。同理,可以得到当r位于其他区域时,使最小的电压矢量,见表2第一行。当上一个采样周期作用的基本电压矢量1~19时,同理可得到下一时刻的最优矢量,预测开关表见表2。
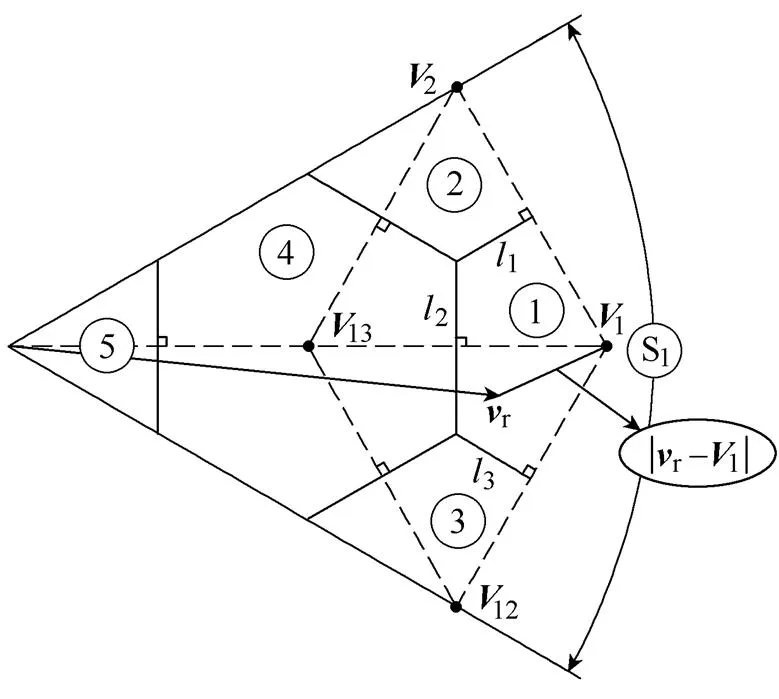
图7 第一扇区区域划分
表2 预测开关表

Tab.2 Predictive switching table
当r位于第一扇区时,根据r所在区域号以及上一个采样时刻作用的电压矢量,可以从表2直接选择出使最小的电压矢量。当r位于其他扇区时,通过简单的扇区变换,表2同样适用。
由于在传统评价函数中,中点电位项的值一般远小于其他项[13],因此对电压矢量影响较大的是磁链和电磁转矩控制项。考虑到从表2可以直接选择出使最小的电压矢量,本文提出的改进策略在第二步预测时,可以通过表2选择出电压矢量作为(+2)s时刻的输出电压矢量。当通过表2选择到小矢量时,考虑到小矢量有两种开关状态,它们对中点电位的作用相反,选择使中点电位平衡的开关状态作为最终输出状态。
2.2 改进MPTC
改进MPTC的算法流程如下:
(1)延迟补偿过程和第一步预测过程,与传统MPTC相同,对有限控制集中所有元素执行模型预测计算后,得到(+2)s时刻的磁链、电磁转矩和中点电位。
(2)将第一步预测得到的磁链和电磁转矩的预测值|s|+2()和e+2()代入式(12)和式(13)进行计算,得到参考电压矢量r+2()。然后判断r+2()所在扇区,再通过比较r+2()与中垂线位置关系判断r+2()所在区域。
(3)根据r+2()所在区域号和(),从表2中选择出+2(),作为(+2)s时刻的输出电压矢量,并将+2()代入式(5)计算(+3)s时刻的中点电位。
(4)两步预测完成后得到条轨迹,改进MPTC预测轨迹如图8所示。每条轨迹中的X+2()代表(+2)s时刻磁链、电磁转矩和中点电位,+2()代表(+2)s时刻输出电压矢量,()代表参考电压矢量r+2()和由+2()计算得到的 (+3)s时刻中点电位值。最后将上述变量值代入改进MPTC评价函数中,即

选取使评价函数最小的预测轨迹,并将这条轨迹对应的 (+1)s时刻的电压矢量作为输出。
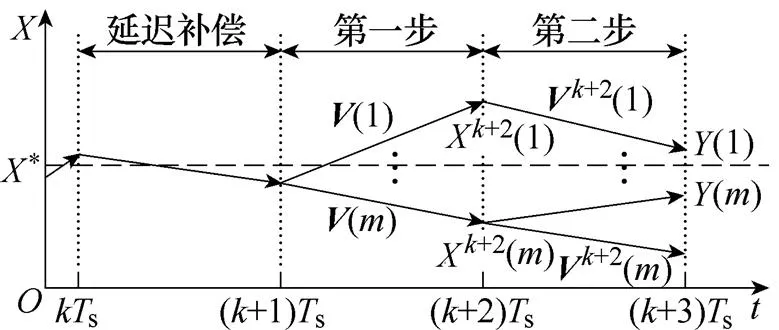
图8 改进MPTC预测轨迹
改进MPTC在第二步预测时,以一次查表代替传统MPTC对N内所有元素的模型预测计算。因此,改进MPTC第二步预测最多只进行7次查表运算。查表过程包括简单的区域判断和查找开关表2,与传统MPTC第二步预测计算过程相比,计算量大大减小。
2.3 参数K取值分析
在改进策略的评价函数中,参数代表了转矩权重系数。权重系数的取值会影响控制性能。取较小的值可以增加控制器对电磁转矩的控制力度,但是过小的会增大磁链波动,进而使电流纹波增加,整体控制性能下降。当取值较大时,电磁转矩波动会增加,同时系统动态响应能力下降。
通常权重系数的取值是通过大量的仿真和实验来确定的[21]。在本文提出的改进算法中,参数可以通过式(9)计算得到,可以看出是负载角的函数。下面对的取值进行仿真分析。记=0时的值为0,对在(0.5~1.5)0的范围内作仿真,分析磁链和电磁转矩的波动变化,仿真采用的电机参数见表3。以磁链和电磁转矩的均方差作为波动衡量标准,即

式中,为磁链或者电磁转矩;为总采样个数;为实际采样值。=0时磁链和电磁转矩波动分别为s0和0,将取其他值时磁链和电磁转矩波动分别与s0和0进行对比,取值对控制性能影响仿真结果如图9所示。
表3 PMSM参数

Tab.3 Parameters of PMSM
从图9中可以看出,随着增加,磁链波动减小,电磁转矩波动增加,这与转矩权重系数的作用相吻合。考虑到在(0.8~1.1)0区间取定值时,磁链和电磁转矩波动均在较为合理的范围,因此可以按照这个范围对进行初步整定,然后根据实际运行情况与控制要求进行调整。

图9 K取值对控制性能影响仿真结果
3 实验
为验证本文算法的可行性和有效性,采用NPC三电平逆变器驱动永磁同步电机实验平台对两步预测MPTC策略进行实验研究,实验系统如图10所示。实验中所用PMSM电机参数见表3。实验中负载电机为一台以西门子变频器S120驱动的11kW异步电机,控制器为浮点微处理器TMS320F28335。

图10 实验系统
DSP运行传统两步预测MPTC程序(包括A-D采样、保护、DAC和核心算法等)计算时间为124ms,而改进MPTC的计算时间为63ms,计算量减小49.19%。对于模型预测转矩控制,缩短采样周期在一定程度上可以提高逆变器的平均开关频率,改善控制性能。改进算法是对传统算法的简化,两者的矢量选择原理本质是相同的。当采样周期相同时,改进算法和传统算法可以获得几乎相同的控制效果。而在充分发挥控制器运算能力的前提下,改进算法可以采用更短的采样周期,这是算法的优势所在。由于DSP运行传统算法的计算时间最小为124ms,考虑一定的时间裕量,在以下实验中传统算法的采样周期设为140ms,改进算法的采样周期设为80ms。
图11和图12分别为传统算法和改进算法控制电机在负载为100N·m时,转速指令从50r/min阶跃至200r/min的实验波形。

图11 传统MPTC转速阶跃实验波形

图12 改进MPTC转速阶跃实验波形
从图11和图12可以看出,电机加速时,转矩调节器迅速达到限幅值,随着转速增加,输出转矩平稳减小,最终实际转速等于转速给定值,输出转矩与负载转矩平衡,转速有微小的超调,中点电位的波动范围不超过2.5%(直流母线电压为400V)。传统算法稳态时磁链s=0.013 1Wb,转矩= 6.45N·m,电流总谐波畸变率为19.37%,改进算法稳态时磁链s=0.009 6Wb,转矩=4.28N·m,电流总谐波畸变率为12.13%。磁链波动、电磁转矩波动和电流畸变率分别减小26.71%、33.64%和37.37%。实验说明由于改进MPTC可以采用更高的采样频率,因此在控制电机转速快速平稳地跟踪给定值的同时,控制效果更好。
图13和图14分别为传统算法和改进算法控制电机在转速为150r/min运行时,负载转矩由空载(负载转矩约15N·m)突加至100N·m的实验结果。

图13 传统MPTC电机突加负载实验波形
从图13和图14可以看出,输出转矩可以快速与负载转矩平衡。在突加负载过程中,电机转速小幅下降后立刻恢复到稳定运行状态。在输出转矩较高时,NPC三电平逆变器中点电位的波动范围增大是由于大、中矢量的使用比重增加,但中点电位的波动范围不超过2.5%(直流母线电压为400V)。传统算法稳态时磁链s=0.012 7Wb,转矩=6.33N·m,电流总谐波畸变率为18.84%,改进算法稳态时磁链s=0.009 7Wb,转矩=4.15N·m,电流总谐波畸变率为11.76%。磁链波动、电磁转矩波动和电流畸变率分别减小23.62%、34.43%和37.6%。实验说明两步预测MPTC可以控制电机稳定输出转矩,改进MPTC采用更高的采样频率使控制效果更好。
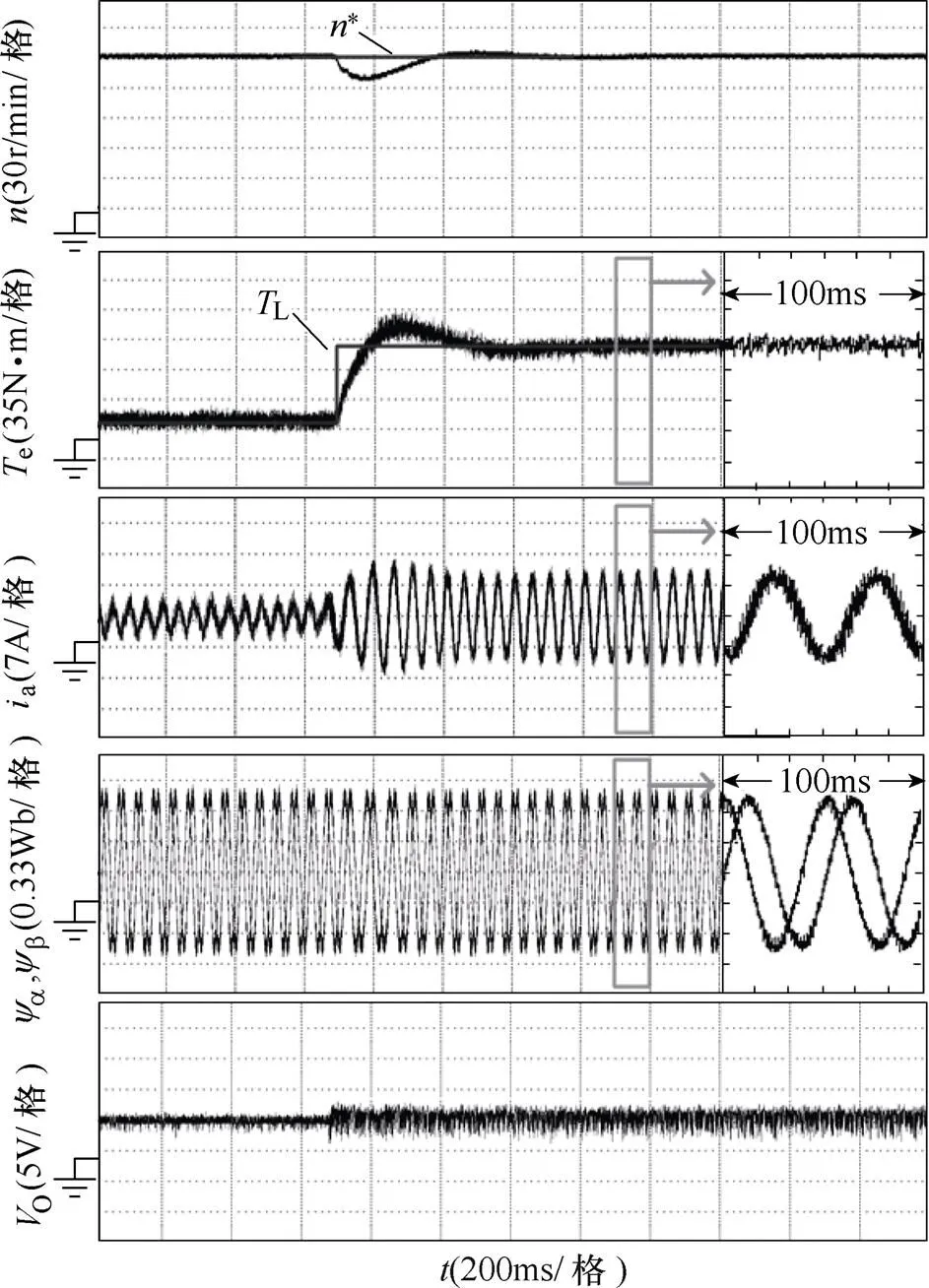
图14 改进MPTC电机突加负载实验波形
4 结论
MPTC可以有效利用逆变器产生的基本电压矢量实现对电机磁链和电磁转矩的控制。本文针对传统两步预测MPTC计算负担较大的问题,提出了结合预测开关表的改进两步预测MPTC策略。将评价函数中磁链和电磁转矩的参考值与实际值之间的关系,变换为参考电压与实际电压之间的关系,选择使参考电压与实际电压矢量差的模最小的电压矢量作为磁链和电磁转矩最优控制电压矢量。根据上述原则,将空间区域合理划分,建立了预测开关表,并将其应用于第二步预测,简化了预测过程。相比传统MPTC,改进算法在实际应用当中的优势在于算法的计算量更小,可以采用更短的采样周期。最后通过实验验证了改进MPTC算法的有效性与可行性。
参考文献:
[1] 邱鑫, 黄文新, 卜飞飞, 等. 电动汽车用IPMSM直接转矩控制系统效率优化[J]. 电工技术学报, 2015, 30(22): 42-48.
Qiu Xin, Huang Wenxin, Bu Feifei, et al. Efficiency optimization of IPMSM direct torque control system used in electric vehicles[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 42-48.
[2] 牛峰, 李奎, 王尧. 基于占空比调制的永磁同步电机直接转矩控制[J]. 电工技术学报, 2014, 29(11): 120-129.
Niu Feng, Li Kui, Wang Yao. Model predictive direct torque control for permanent magnet synchronous machines based on duty ratio modulation[J]. Transa- ctions of China Electrotechnical Society, 2014, 29(11): 120-129.
[3] 梅杨, 孙凯, 黄震. 二极管中点钳位型三电平逆变器-交流电机调速系统的高精度建模与分析[J]. 电工技术学报, 2015, 30(6): 200-207.
Mei Yang, Sun Kai, Huang Zhen. High accuracy modeling and analysis of neutral-point-clamped three-level inverter fed AC motor drive system[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 200-207.
[4] 王若醒, 吴迎霞, 杨恢宏, 等. 两级式T型三电平光伏逆变器的关键技术研究及实现[J]. 电力系统保护与控制, 2015, 43(4): 58-62.
Wang Ruoxing, Wu Yingxia, Yang Huihong, et al. Research on key technologies of double-stage T-type three-level photovoltaic inverter[J]. Power System Protection and Control, 2015, 43(4): 58-62.
[5] 李永东, 侯轩, 谭卓辉. 三电平逆变器异步电动机直接转矩控制系统 (I)——单一矢量法[J]. 电工技术学报, 2004, 19(4): 34-39.
Li Yongdong, Hou Xuan, Tan Zhuohui. Direct torque control of induction motor fed by three level inverter (I)——single vector method[J]. Transactions of China Electrotechnical Society, 2004, 19(4): 34-39.
[6] 宋文胜, 冯晓云, 侯黎明, 等. 电力牵引传动系统的三电平直接转矩控制算法的半实物实验研究[J]. 电工技术学报, 2012, 27(2): 165-172.
Song Wensheng, Feng Xiaoyun, Hou Liming, et al. Hardware-in-loop research of three-level direct torque control scheme for electric traction drive system[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 165-172.
[7] Mohan D, Zhang X N, Foo G. Direct torque control of IPMSM driven by a three level NPC inverter with torque and capacitor voltage ripple reduction[C]// Applied Power Electronics Conference and Exposition (APEC), Charlotte, 2015: 557-564.
[8] Zhang Y C, Zhu J G, Zhao Z M, et al. An improved direct torque control for three-level inverter-fed induction motor sensorless drive[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(3): 1502- 1513.
[9] 李永东, 侯轩, 谭卓辉. 三电平逆变器异步电动机直接转矩控制系统 (Ⅱ)——合成矢量法[J]. 电工技术学报, 2004, 19(5): 31-35.
Li Yongdong, Hou Xuan, Tan Zhuohui. Direct torque control of induction motor fed by three level inverter (II)——method of synthesizing vectors[J]. Transa- ctions of China Electrotechnical Society, 2004, 19(5): 31-35.
[10] 刘述喜, 王明渝. 基于快速空间矢量调制算法的三电平直接转矩预测控制系统[J]. 电工技术学报, 2009, 24(2): 35-41.
Liu Shuxi, Wang Mingyu. Direct torque predictive control system supplied by three-level inverter based on a fast SVPWM algorithm[J]. Transactions of China Electrotechnical Society, 2009, 24(2): 35-41.
[11] 林磊, 邹云屏, 王展, 等. 一种具有中点平衡功能的三电平异步电机直接转矩控制方法[J]. 中国电机工程学报, 2007, 27(3): 46-50.
Lin Lei, Zou Yunping, Wang Zhan, et al. A DTC algorithm of induction motors fed by three-level inverter with neutral-point balancing control[J]. Proceedings of the CSEE, 2007, 27(3): 46-50.
[12] 朱玲, 符晓巍, 胡晓波, 等. 模块化多电平变流器HVDC系统的模型预测控制[J]. 电力系统保护与控制, 2014, 42(16): 1-8.
Zhu Ling, Fu Xiaowei, Hu Xiaobo, et al. Model predictive control of modular multilevel converter for HVDC system[J]. Power System Protection and Control, 2014, 42(16): 1-8.
[13] 王峰, 张旭隆, 何凤有, 等. 基于复合模型预测控制策略的三电平APF研究[J]. 电力系统保护与控制, 2014, 42(11): 79-85.
Wang Feng, Zhang Xulong, He Fengyou, et al. Research of three-level shunt APF control method based on composite model predictive control strategy[J]. Power System Protection and Control, 2014, 42(11): 79-85.
[14] 杨冬锋, 周苏荃, 魏剑啸, 等. 基于MPC的超短期优化调度策略研究[J]. 电力系统保护与控制, 2015, 43(11): 21-25.
Yang Dongfeng, Zhou Suquan, Wei Jianxiao, et al. Ultra-short term optimal dispatch method based on MPC[J]. Power System Protection and Control, 2015, 43(11): 21-25.
[15] Geyer T, Papafotiou G, Morari M. Model predictive direct torque control—part I: concept, algorithm, and analysis[J]. IEEE Transactions on Industrial Elec- tronics, 2009, 56(6): 1894-1905.
[16] Stolze P, Karamanakos P, Kennel R, et al. Variable switching point predictive torque control for the three-level neutral point clamped inverter[C]//15th European Conference on Power Electronics and Applications, Lille, 2013: 1-10.
[17] 沈坤, 章兢, 王坚. 一种多步预测的变流器有限控制集模型预测控制算法[J]. 中国电机工程学报, 2012, 32(33): 37-44.
Shen Kun, Zhang Jing, Wang Jian. A model predictive control scheme of multi-step prediction finite control set for converters[J]. Proceedings of the CSEE, 2012, 32(33): 37-44.
[18] Xie W, Wang X C, Wang F X, et al. Finite control set-model predictive torque control with a deadbeat solution for PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5402-5410.
[19] 朱昊, 肖曦, 李永东. 永磁同步电机转矩预测控制的磁链控制算法[J]. 中国电机工程学报, 2010, 30(21): 86-90.
Zhu Hao, Xiao Xi, Li Yongdong. Stator flux control scheme for permanent magnet synchronous motor torque predictive control[J]. Proceedings of the CSEE, 2010, 30(21): 86-90.
[20] Preindl M, Bolognani S. Model predictive directtorque control with finite control set for PMSM drive systems, part 1: maximum torque per ampere operation[J]. IEEE Transactions on Industrial Infor- matics, 2013, 9(4): 1912-1921.
[21] 张永昌, 杨海涛. 感应电机模型预测磁链控制[J]. 中国电机工程学报, 2015, 35(3): 719-726.
Zhang Yongchang, Yang Haitao. Model predictive flux control for induction motor drives[J]. Pro- ceedings of the CSEE, 2015, 35(3): 719-726.
Model Predictive Torque Control with Switching Table for Neutral Point Clamped Three-Level Inverter-Fed Permanent Magnet Synchronous Motor
1,21111
(1. School of Electrical Engineering and Automation Tianjin UniversityTianjin 300072 China;2. Tianjin Engineering Center of Electric Machine System Design and Control Tianjin 300387 China)
A model predictive torque control (MPTC) is proposed for a neutral point clamped (NPC) three-level inverter based permanent magnet synchronous motor (PMSM) drive system. The flux and torque components in the cost function are equivalent to the amplitude of the difference between reference voltage vector and the basic voltage vector. By dividing the vector space logically, a predictive switching table is built. The built switching table can select the voltage vector which minimizes the amplitude mentioned above. The selected vector is then used as the output of the second step prediction. Thereby multiple model predictive calculations of the second step prediction are replaced by selecting a vector from switching table. The experimental results show that the improved MPTC strategy controls the flux, torque and neutral point voltage effectively. Compared with the traditional MPTC method, the improved MPTC strategy also has lower computation.
Neutral point clamped three-level inverter, permanent magnet synchronous motor, model predictive torque control, predictive switching table
TM351
夏长亮 男,1968年生,教授,博士生导师,研究方向为电机系统及其控制、电力电子与电气传动、风力发电系统运行控制。
E-mail: motor@tju.edu.cn(通信作者)
张天一 男,1990年生,硕士研究生,研究方向为永磁同步电机直接转矩控制。
E-mail: zhang_303607@163.com
2015-09-28 改稿日期 2016-01-06
国家重点基础研究发展计划(973计划)资助项目(2013CB035600)。
