利用三频外差实现的小视场三维测量系统
2016-11-17刘守起刘元坤张启灿
艾 佳,刘守起,刘元坤,张启灿
利用三频外差实现的小视场三维测量系统
艾 佳,刘守起,刘元坤,张启灿
( 四川大学电子信息学院光电系,成都610064 )
搭建了一套小视场的三维面形测量系统。该测量系统采用基于DLP4500芯片开发的高速数字投影模块套件实现条纹图像的高速投影和相机的同步触发图像采集。利用该投影模块向小视场物体表面投影三种不同频率的相移条纹图,相机同步记录受到物体表面形貌调制而发生形变的条纹,分别计算出三组条纹对应的截断相位图,再进行两次外差得到频率为1的相位分布,以此为基准往回展开得到连续的相位分布,从而重建被测物体的三维面形分布。实验成功重建了以硬币为代表的小视场(8 mm×6 mm)物体在100 μm深度范围内的表面三维形貌。
三维测量;三频外差法;相移;时间相位展开
0 引 言
目前,结构光三维测量技术[1]在许多领域得到了广泛的应用。经过几十年的发展,产生出了多种方法,包括傅里叶变换轮廓术[2]、相位测量轮廓术、调制度测量轮廓术[3]等。这些方法大多应用于常规尺寸和大视场物体的测量。但随着机械加工技术、微电子技术、材料技术等领域的发展,越来越多的行业对小物体的三维表面轮廓信息产生了需求。
近十年来,国内外多位专家学者提出了针对小物体表面形貌的测量方法。任晨丽[4]等人提出了一种基于三坐标测量机的小视场多目立体测量方法。Quan[5]等人搭建了一套小视场三维测量系统,在相位展开时采用的是空间相位展开的方法。陈超[6]等人利用立体显微镜搭建了一套基于彩色条纹投影的小视场测量系统。本文设计实现的微小视场三维面形测量系统,结构简单,在相位展开时采用的是时间相位展开方法[7]中的三频外差算法[8-9]。三频外差法投影的条纹图数较少,能够在保证较高测量精度的情况下,提高测量速度,可以应用于静态微小物体的表面形貌测量。本文的测量系统是利用基于DLP4500芯片开发的投影组件投影微小视场的正弦条纹到微小物体表面,搭配与投影组件同步触发控制的CCD相机采集变形条纹图,经过三频外差算法处理获取的这些条纹图像,实现了对静态微小物体表面形貌的三维测量与重建。
文中第一节介绍了此测量系统进行三维形貌测量的基本原理;第二节给出了实际测量结果;第三节对实验结果进行了分析,并做出总结。
1 相移技术及三频外差法的三维形貌检测基本原理
相位测量轮廓术是V. Srinivasan和M. Halioua[10-11]等人提出。其基本原理是投影有固定相位差的多幅正弦条纹图样到待测物体表面,之后利用CCD采集回来的相应变形条纹来计算相位,最终通过高度映射重建被测物体的三维面形。测量光路如图1所示。

图1 测量原理图
图中,1、2分别为投影系统的入瞳和出瞳,3、4为成像系统的入瞳和出瞳,表示成像系统入瞳3到参考平面的距离,表示投影系统出瞳2和成像系统入瞳3之间的距离,Grating为投影的正弦光栅,CCD为成像系统。
当投影正弦条纹到三维漫反射物体表面上,通过成像系统采集,得到的变形条纹强度可以表示为
由于是通过反正切函数计算相位信息,因此所得的相位值都是被截断在区间内的不连续相位。为了得到连续的相位分布,需要进行相位展开。本文采用三频外差方法进行相位展开。
三频外差法是一种时间相位展开方法,它是在三频展开法[12]的基础上改进而来。通过投射三种不同频率的条纹图到物体表面,拍摄得到一组受物体表面调制的条纹图序列,然后将每点的相位沿时间序列独立进行展开,可以从原理上避免误差的传播[13-15]。
纹图,其中外差即对应像素点相位相减。
到的斜率表示为
其中:,,为标定后测量系统的相关参数,可以通过四平面法[16-17]标定测量系统得到。即为计算得到的物体表面的高度信息。
2 实验结果
基于上述原理,本文搭建了一套适于测量微小物体形貌的测量系统,其测量装置如图2所示。

图2 测量系统装置图
本测量系统使用了一款基于DLP4500芯片开发的高速数字投影套件,经0.8倍率、工作距离为110 mm的远心镜头,投影不同频率的相移正弦条纹到小视场(8 mm×6 mm)物体表面,并对CCD相机(配有和投影系统相同的远心镜头)进行同步触发控制,实现条纹图像的高速投影和相机的同步采集,利用四步相移和三频外差法对微小物体的表面三维形貌进行了测量和重建。
本文测量的微小物体为日常生活中常见的一角硬币和身份证上的微小局部形貌,待测物体如图3所示。投影十二幅三种不同频率的条纹图到物体表面,四步相移条纹投影条纹频率依次为1/42、1/49、1/57,表示的是此时四步相移条纹投影条纹的周期数依次为42、49、57,频率依次对应为1 280/42 pixel-1、1 280/49 pixel-1、1 280/57 pixel-1。

图3(a) 待测一角硬币表面测量区域
Fig.3(a) Digital character ‘1’ and Chinese character ‘Jiao’ on a coin

图3(b) 待测身份证“华”字
Fig.3(b) Chinese character ‘Hua’ on an ID card
采集得到一角硬币“1”字表面投影条纹频率为1/42的一组变形条纹图如图4所示,图像分辨力大小为1 360 pixels×1 024 pixels。
然后利用四步相移法计算得到三种不同频率的截断相位图如图5所示。

图5 三种频率条纹经处理后得到的一角硬币“1”字的截断相位图
利用三频外差法的原理对其进行展开,得到展开相位。再对测量系统进行四平面法标定得到参数,,,代入式(8)可以对展开相位进行高度映射。最终得到图6所示的一角硬币上“1”字的三维面形重建结果。

图6 一角硬币“1”字重建结果
类似地对一角硬币的“角”字部分进行测量,采集得到的投影条纹频率为1/42的一帧变形条纹图如图7(a)所示,最终的重建结果如图7(b)所示。重建面形的纹波调制,是由于投影条纹中还存在少量的高次谐波所导致的相位误差引起的,在进行系统修正补偿后,该误差是可以最终削弱和消除的。

图7 (a) 投影条纹频率为1/42时,“角”字表面的一帧变形条纹图
Fig.7(a) The deformed fringes (=1/42) ofChinese character ‘Jiao’

图7(b) 一角硬币“角”字重建结果
Fig.7(b) The restored height distribution of digital Chinese character ‘Jiao’

图8(a) 投影条纹频率为1/42时,身份证“华”字表面的一帧变形条纹图
Fig.8(a) The deformed fringes (=1/42) of Chinese character ‘Hua’ on an ID card
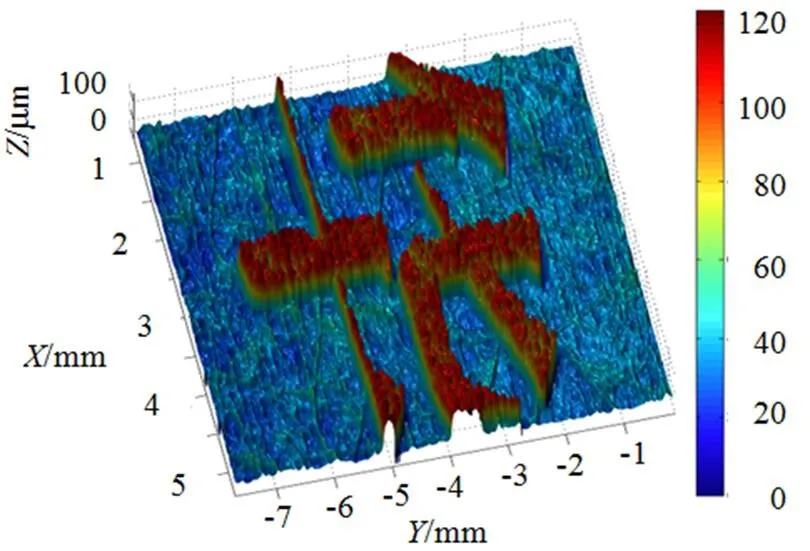
图8(b) 身份证“华”字重建结果
Fig.8(b) The restored height distribution of digital Chinese character ‘Hua’
对身份证“华”字部分进行测量,投影的条纹频率不变,利用同样的方法,成功对其进行了重建,投影的一帧条纹如图8(a)所示,对应重建结果如图8(b)所示。
利用标准平面进行系统测量精度初步评估的结果表明,本文设计的系统目前的测量深度范围为380 μm,系统精度为10 μm(标准偏差),向灵敏度优于2 μm。如果进一步优化系统硬件结构参数,增加投影条纹的周期数,系统的测量精度将能得到提升。
3 结 论
三维表面测量在工业检测、机器视觉等领域有着重要作用,并且其应用领域在未来将进一步拓展,而基于结构光的非接触测量是实现三维表面测量的一个重要手段,有着广阔的应用前景。本文基于相移技术并结合三频外差法的原理,利用投影模块的快速投影和CCD相机同步采集,搭建了一套微小视场(8 mm×6 mm)下物体表面形貌的测量系统。实验结果表明,本文所搭建的系统投影三种频率、四步相移的十二幅条纹图,能对微小物体表面形貌进行重建。
参考文献:
[1] 苏显渝,李继陶,曹益平,等. 信息光学:二版[M]. 北京:科学出版社,2013:304-307.
[2] 许平,陈文静,苏显渝. 高精度的数字光投影傅里叶变换轮廓术 [J]. 光电工程,2005,32(11):59-62.
XU Ping,CHEN Wenjing,SU Xianyu. Higher-precision FTP based on digital light projecting [J]. Opto-Electronic Engineering,2005,32(11):59-62.
[3] 邵双运,苏显渝. 调制度测量轮廓术高度信息获取新算法 [J]. 光电工程,2005,32(9):43-54.
SHAO Shuangyun,SU Xianyu. New depth recovery algorithm in modulation measurement profilometry [J]. Opto-Electronic Engineering,2005,32(9):43-54.
[4] 任晨丽,仲思东. 小视场多目立体测量系统的研究 [J]. 计算机工程与应用,2006,42(18):65-67.
REN Chenli,ZHONG Sidong. Study on Multi-Sensor Stereovision Measurement System in Small Field [J]. Computer Engineering and Applications,2006,42(18):65-67.
[5] QUAN C,HE X Y,WANG C F,. Shape measurement of small objects using LCD fringe projection with phase shifting [J]. Optics Communications(S0030-4018),2001,189(1/3):21–29.
[6] 陈超. 基于彩色条纹投影的三维小视场成像系统软硬件开发 [D]. 天津:河北工业大学,2014:5-11.
CHEN Chao. Hardware and software development of three-dimensional small field imaging system based on color fringe projection [D]. Tianjing:Hebei University of Technology,2014:5-11.
[7] 岳慧敏. 基于时间相位展开的三维轮廓测量研究 [D]. 成都:四川大学,2005:16-29.
YUE Huimin. Research on three-dimensional profilometry based on temporal phase unwrapping [D].Chengdu:Sichuan University,2005:16-29.
[8] Carsten Reich,Reinhold Ritter,JAN Thesing. White light heterodyne principle for 3D-measurement [C]// Sensors,Sensor Systems,and Sensor Data Processing,Munich,FRG,June 16-17,1997,3100:236-344.
[9] 黄燕钧,李中伟,史玉升,等. 基于多频外差原理的三维测量技术 [J]. 新技术新工艺,2008(12):37-40.
HUANG Yanjun,LI Zhongwei,SHI Yusheng,. 3D Measurement Technology Based on Multifrequency Heterodyne Principle [J].New Technology & New Process,2008(12):37-40.
[10] Srinivasan V,LIU H C,Halioua M. Automated phase-measuring profilometry of 3-D object shapes [J]. Applied Optics(S1559-128X),1984,23(18):3105-3108.
[11] Maurice Halioua,LIU Hsin-Chu. Optical three-dimensional sensing by phase measurement profilometry [J]. Optics and Lasers in Engineering(S0143-8166),1989,11:185-215.
[12] 徐珍华,苏显渝. 一种时间相位展开算法 [J]. 四川大学学报:自然科学版,2008,45(3):537-540.
XU Zhenhua,SU Xianyu. An algorithm of temporal phase unwrapping [J]. Journal of Sichuan University:Natural Science Edition,2008,45(3):537-540.
[13] 李璐璐,苏显渝,窦蕴甫,等. 时间相位展开的误差分析与算法设计 [J]. 四川大学学报:自然科学版,2012,49(1):102-108.
LI Lulu,SU Xianyu,DOU Yunfu,. Error analysis and algorithm design of temporal phase unwrapping [J].Journal of Sichuan University:Natural Science Edition,2012,49(1):102-108.
[14] Huntley J M,Saldner H O. Temporal phase-unwrapping algorithm for automated interferogram analysis [J]. Applied Optics(S1559-128X),1993,32(17):3047-3052.
[15] Huntley J M,Saldner H O. Error-reduction methods for shape measurement by temporal phase unwrapping [J]. Journal of the Optical Society of America A(S0740-3232),1907,14(12):3188-3196.
[16] 马颂德,张正友. 计算机视觉:计算理论与算法实现 [M]. 北京:科学出版社,1998:52-60.
[17] 李万松. 位相测量轮廓术(PMP)应用研究 [D]. 成都:四川大学,1999:79-93.
LI Wansong. Applied Study on Phase Measuring Profilometry [D]. Chengdu:Sichuan University,1999:79-93.
Three-dimensional Small-field Measurement System Based on Tri-frequency Heterodyne Fringe Analysis
AI Jia,LIU Shouqi,LIU Yuankun,ZHANG Qican
( Opto-electronics Department, College of Electronic Information, Sichuan University, Chengdu 610064, China )
A three-dimensional (3D) shape measuring system has been built. In the system, a high-speed digital projection module was developed with a DLP4500 chip and synchronously trigged with a CCD camera. Three different frequencies fringe patterns were projected onto the surface of a tested object in turns and were used to calculate the natural phase distribution, as well as the height distribution of the measured object by phase-shifting algorithm and heterodyne phase unwrapping method. Several practical experiments were carried out some tested samples in a small field of view (8 mm×6 mm). The results show that the system can restore the objects’ (coins for example) 3D shape (~100 μm) with a high accuracy.
3D shape measurement; tri-frequency heterodyne method; phase shifting; temporal phase unwrapping
1003-501X(2016)09-0039-06
TN247
A
10.3969/j.issn.1003-501X.2016.09.007
2015-12-11;
2016-01-30
国家重大仪器专项(2013YQ490879)资助项目
艾佳(1988-),男(汉族),江西吉安人。硕士,主要研究工作是三维测量。E-mail: aijiaupt@126.com。
张启灿(1974-),男(汉族),云南陆良人。教授,博士,主要研究工作是三维传感、动态三维测量等。E-mail: zqc@scu.edu.cn。
