带干扰观测器的PID控制器设计与仿真

西安铁路职业技术学院电气工程系 王 丹

带干扰观测器的PID控制器设计与仿真

西安铁路职业技术学院电气工程系 王 丹

本文通过设置干扰观测器，解决了PID控制方法中内扰无法观测的问题。并通过仿真证明，该控制系统不仅能够提高系统输出跟踪系统输出的能力，而且能够更快地消除内扰，从而提高系统的鲁棒稳定性和抗干扰能力。

干扰观测器；PID控制；仿真

0　引言

PID控制方法基于系统的精确模型，结构简单，并能有效地抑制阶跃干扰，工作可靠，但其对周期性的交变干扰抑制能力较差，在控制非线性、时变、耦合及参数和结构复杂过程时，很难实现精确的控制。本文采用对系统中的干扰进行补偿的方法对其加以抑制。此方法无需额外的力或力矩传感器，实现简单；能有效抑制阶跃和交变干扰，具有较强的鲁棒性；在一定的模型误差范围内，具有响应快和可独立调整的特点，方法灵活，易于控制。

1　干扰观测器的研究

干扰观测器基本思想是［3］将外部力矩干扰以及模型参数的变化造成的实际对象与名义模型输出的差异等效到控制的输入端，即观测出等效干扰。基于这种引入等效的补偿思想设计出的干扰观测器的原理框图如图1所示。

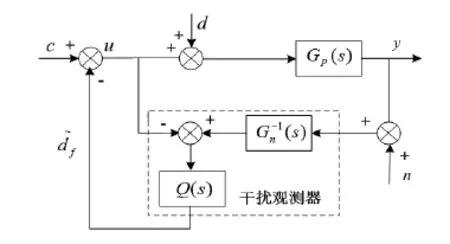
图1　干扰观测器结构框图

如图1所示中c为PID控制器的输入，y为输出信号，n为检测噪声信号。GP（s）为控制对象的传递函数。Q（s）为串入的低通滤波器。Gn（s）为标称模型，G-1n（s）来代替GP（s），目的是解决精确模型不易得到等实际问题。

等效干扰的估计值 在模型匹配情况下，代表实际干扰d。如下式：

控制对象的传递函数模型Gn（s），将不确定对象的集合用乘积来描述，有：

忽略非建模动态和不确定性的影响，Gn（s）可表示：

其中，Jn为等效惯性力矩，bn为等效阻尼系数。

由干扰观测器的原理框图可知：

其中：Y（s）为输出函数，C（s）输入函数，D（s）为干扰，N（s）为检测噪声，GCY（s）表示从输入c到输出y的传递函数，GNY（s）是从干扰到输出的传递函数， 从检测噪声到输出的传递函数。

2　低通滤波器的设计

设低通滤波器Q（s）的频带为fq，有：

低通滤波器Q（s）的设计是干扰观测器设计中的一个重要环节，通过对Q（s）的设计可较好的抵抗外加干扰。

由鲁棒稳定性定理，低通滤波器Q（s）鲁棒稳定的充分条件是：

由式（8）设计出本文采用的低通滤波器为：

通过对Q（s）的设计，可实现鲁棒性要求。

3　实例控制仿真

设被控对象为：

则名义模型取为：

加入干扰观测器的仿真模块如图6所示。

图2　无干扰观测器仿真模块

图3　干扰信号

图4　正弦跟踪图

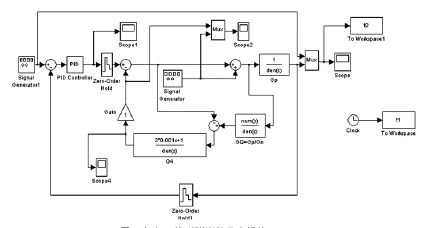
图5　加入干扰观测器的仿真模块

图6　正弦跟踪图

从有无干扰观测器的仿真曲线可以看出：没有干扰观测器即只采用PID控制时，加入干扰信号正弦的跟踪曲线产生波动，不能较好的跟踪系统的输出；在PID的控制中加入了干扰观测器，加快了消除内扰的过程，能够提高跟踪系统输出的能力。

4　结论

本文针对常规PID控制存在的不足，在PID控制中加入干扰观测器。仿真结果说明，在基于干扰观测器的PID控制能有效抑制周期交变干扰，从而使系统的鲁棒性和抗干扰能力都得到了提高。同时，基于干扰观测器的PID控制实现简单，方法灵活，具有实际应用前景。

［1］张平，苑明哲，王宏.基于干扰观测器的污水处理过程控制研究［J］.计算机工程与设计，2006，7，27（14）：2601-2603.

［2］文广，章甫，赵丁选.新型力反馈双向伺服系统干扰观测器PID控制算法的研究［J］.重庆邮电学院学报（自然科学版），2006，18（2）.

［3］焦嵩呜，韩璞，董泽.带有干扰观测器的PID的CMAC控制系统设计［J］.系统仿真学报，2007，19（22）.

［4］李向国，梅志千，王永秀.倒立摆伺服系统中的干扰补偿控制［J］.微特电机，2008（ll）.

［5］刘金琨.先进PID控制MATLAB仿真［M］.北京：电子工业出版社，2005，8.