螺旋溜槽分选流场中矿粒运动轨迹研究

刘祚时，赵南琪，刘惠中，2，李华梁

螺旋溜槽分选流场中矿粒运动轨迹研究

刘祚时1，赵南琪1，刘惠中1，2，李华梁1

（1.江西理工大学机电工程学院，江西赣州341000；2.北京矿冶研究总院，北京100160）

为研究矿粒在螺旋溜槽分选流场中的运动轨迹，以BL600螺旋溜槽作为基础，利用FLUENT软件、离散相颗粒模型（DPM），建立了螺旋溜槽分选CFD模型，分析了分选效果与矿物颗粒比重及粒度的关系，阐明了螺旋溜槽分选流场中矿物颗粒运动轨迹规律。仿真结果与已有的螺旋溜槽在分选矿物颗粒运动轨迹研究相吻合，揭示了螺旋溜槽设备重选分选原理，证明了此CFD模型的可靠性，此模型的建立也为今后螺旋溜槽结构的改进优化提供了新的方法。

螺旋溜槽；CFD模型；分选过程；颗粒运动轨迹

螺旋溜槽应用广泛，分选能力优秀，主要得益于其较为独特的分选流场，研究分选时矿物颗粒在其分选流场中的运动轨迹显得尤为重要［1-2］。但因其分选流场较为复杂，且矿物颗粒在流场中的受力极为繁杂，对其直接进行理论计算分析，显得较为困难。随着CFD技术的发展，采用流体力学FLUENT分析软件对该问题进行模拟分析成为可能［3］。

作为流膜类重选设备的典型代表，螺旋溜槽在分选过程中，水流不仅具有绕轴的螺旋运动（切向流速），而且在过水断面内还存在着断面环流（径向流速）。这两种运动的合成，就构成了螺旋槽内流体所特有的三维空间的“复合螺旋线”运动［4］。同时在流膜中不同粒度、不同比重矿粒随机的成群运动，导致矿粒的受力变得更加复杂，如颗粒间相互碰撞及摩擦产生的力等，且矿粒在流膜中的沉降方式为干涉沉降，这些因素进一步影响了对分选机理和强化分选效果的深入研究［5-6］。

1　数值模拟的模型及边界条件

通常求解流场中粒子的轨道模型，常采用FLUENT中的离散相模型（Discrete Phase Model，DPM），来跟踪每个颗粒的运动轨迹［7］。故对于研究螺旋溜槽流场中矿物颗粒的运动轨迹，可采用DPM模型得到相似解［8］，具体设置见表1。

表1　离散相颗粒模型（DPM）中主要参数设定表Tab.1　Parameters of discrete phase model（DPM）

模拟仿真所用溜槽是基于北京矿冶研究总院BL600型螺旋溜槽相关技术参数在SolidWorks中创建的。BL600螺旋槽设计相关参数如表2。

表2　BL600螺旋溜槽技术参数Tab.2　Parameter of BL600 spiral concentrator

转换格式导入到ANSYS软件后，具体网格划分及边界条件设置见图1、图2。

图1　螺旋槽计算域网格划分Fig.1　Computational domain mesh of spiral slot

图2　计算域边界条件选择Fig.2　Condition selection of calculation boundary

在螺旋溜槽选矿中，矿物分选完成后，有用的比重大的矿物靠近内缘，脉石、泥砂比重小的靠近外缘，这时通过螺旋槽下部出口的截矿器对精矿、中矿、尾矿进行截取，获得最终产品，分选效果的好坏与矿浆中不同比重差异的物料能否形成良好的分带是有密切联系的。

因此选择方铅矿（7 600 kg/m3）、硫铁矿（4 500 kg/m3）、石英矿（2 650 kg/m3）三种梯度密度矿石分别对1 μm、20 μm、50 μm、100 μm四种梯度粒度的分选轨迹进行数值模拟。

根据国外文献资料及摸索尝试，对于螺旋溜槽矿物颗粒的分选轨迹的轨道模型采用雷诺应力模型（RSM），可以获得最佳的矿物颗粒分选轨迹［9］。

雷诺应力模型（RSM）如式：

式中的变量均为连续相，等式的最后一项∏Rij需考虑连续和分散相的湍流之间的相互作用。其中∏Rij的一般形式可为：

其中C1和C2为未知系数，adc，i为相对速度，bdc，i为漂移速度或相对速度，Rdc，ij为未知颗粒流体相关速度。

为了简化该项，假设：

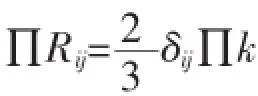
其中δij为克罗内克变量，∏k为原始西莫宁模型的变式：

2　螺旋溜槽颗粒运动轨迹

观察方铅矿（图3）、硫铁矿（图4）、石英矿（图5）等矿物在50 μm、100 μm的粒度下的轨迹图，可以看出矿物颗粒刚进入螺旋槽入口时处于弥散状态，并逐渐开始向内缘聚拢，在经过大约2.5圈后，矿物颗粒都集中在靠近内缘位置运动，实现了矿物分选过程中分带这一环节，并最终沿着内缘从螺旋槽下部出口处排除，完成分选。而对于粒度1 μm的矿物颗粒效果不明显。

图3　方铅矿在四种梯度粒度下的轨迹模拟结果Fig.3　Trajectory simulation results of Galena in four gradient granularities

图4　硫铁矿在四种梯度粒度下的轨迹模拟结果Fig.4　Trajectory simulation results of Pyrite in four gradient granularities

图5　石英矿在四种梯度粒度下的轨迹模拟结果Fig.5　Trajectory simulation results of Quartz in four gradient granularities

为了更明显直观地发现矿物颗粒的运动轨迹规律，单独选取粒度为50 μm的方铅矿（7 600 kg/m3）中的两个颗粒，方便对其进行研究分析，如图6所示，图7为图6在x-z平面的投影。

图6　粒度50 μm方铅矿颗粒轨迹Fig.6　Motion trajectory for 50 μm galena particle

图7　方铅矿颗粒运动轨迹曲线（x-z平面）Fig.7　Galena particle trajectory curve（x-z）

BL600螺旋溜槽的螺旋槽直径是约0.6 m，内缘直径为0.1 m。从图7中可以看出，某两颗方铅矿颗粒在0 s时位于在螺旋槽最外缘（半径为0.3 m）处，分选开始后运动直径逐渐不断缩小，在大约2.5圈（7 s）后，运动直径便维持在了0.1 m（贴在内缘），在剩下的三圈里一直以直径为0.1 m的螺旋线运动，并最终完成了整个分选过程，共耗时10.5s左右。

为方便通过螺旋溜槽矿粒分选轨迹图来阐释该重选设备分选原理，将粒度20 μm的三种不同比重矿物分选轨迹单独集中在一起分析，如图8所示。比重越大矿粒越快进入螺旋槽内缘即精矿区域，而小比重矿粒（硫铁矿和石英矿），由于受到挤出效应的影响，导致进入精矿区域的概率大大降低，只能集中在外侧中尾矿区域，从而达到轻重矿物的分带，实现了按比重差分选，这也正验证了螺旋溜槽设备的重选分选原理。

图8　粒度20 μm下三种矿物颗粒分选轨迹Fig.8　Separationtrajectoryofthreekindsmineral（particleis20μm）

2.1分选效果与矿物比重的关系

螺旋溜槽是借助有用矿石与脉石之间的比重差异实现分选的，对于分选效果的好坏，或者物料能否顺利实现分选，最关键因素就是分选物料中矿物的比重差异。

图9　粒度100 μm三种矿物的分选收集率Fig.9　Cumulative weight distribution of three kinds of 100 μm minerals

图10　粒度50 μm三种矿物的分选收集率Fig.10　Cumulative weight distribution of three kinds of 50 μm minerals

图11　粒度20 μm三种矿物的分选收集率Fig.11　Cumulative weight distribution of three kinds of 20 μm minerals

图12　粒度1 μm三种矿物的分选收集率Fig.12　Cumulative weight distribution of three kinds of 1 μm minerals

图9、图10、图11、图12是三种矿在四种不同粒度的分选收集率［5］。三种矿物比重由高到低分别为方铅矿（7 600 kg/m3）、硫铁矿（4 500 kg/m3）、石英矿（2650kg/m3）。在四幅图中除图12中粒度为1μm时收集率曲线几乎重合一起，没有明显差异外，其他三幅图中不同粒度，随着矿物颗粒比重的递增，其分选收集率的曲线斜率也在明显增大，变得更陡，曲线投影的径向距离越短。表明：大比重矿物颗粒更容易在更短的径向距离内完成分选过程，其矿带的带宽相对更窄，进入到螺旋槽内缘精矿区分选成为精矿产品的概率更大，而比重较小的矿物颗粒在由于带宽更大，且由于精矿区大比重矿粒的挤出效应，则只能进入到外侧中尾矿区成为中尾矿产品。

分选过程中，矿粒由于比重的不同，导致进入内缘精矿区的难易程度不一样，最终形成各自运动带宽半径的不同，实现了不同比重差异矿粒的分选，这证明了矿物颗粒的比重是影响分选效果的关键因素。

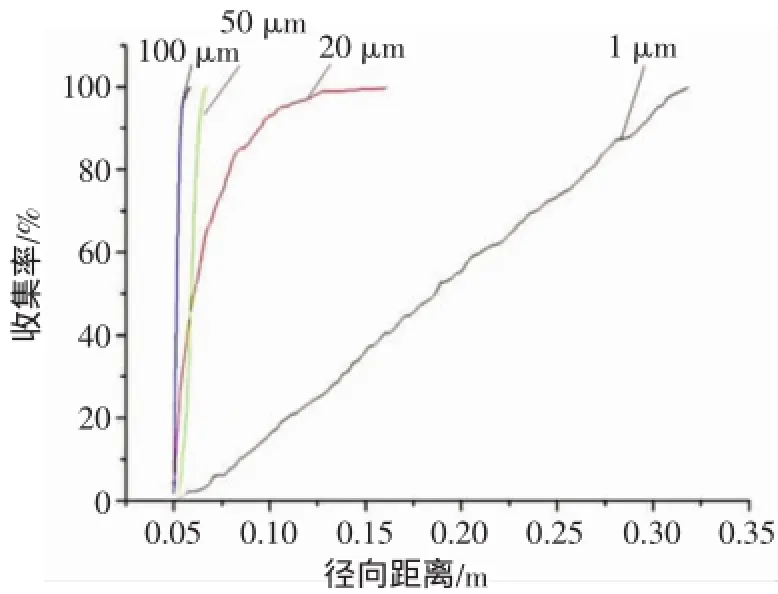
图13　方铅矿各粒度分选收集率Fig.13　Cumulative weight distribution of Galena

图14　硫铁矿各粒度分选收集率Fig.14　Cumulative weight distribution Pyrite

2.2分选效果与矿物粒度的关系

根据三种矿物各粒度分选收集率（图13～图15）可以看出，分选效果与粒度是有一定的关系的，从图13、图14、图15中可以看出三种矿物随着粒度的增大，其曲线明显变更陡，表明矿物颗粒可以在更短径向距离内进入到内缘完成分选，产生更好的分选效果。尤其是粒度大于20 μm以后，曲线斜率明显陡增。但粒度为1 μm时，由于其矿物粒度过小，螺旋溜槽对其影响效果不明显，导致其三种的矿物的曲线斜率变化都不明显。所以，可以看出螺旋溜槽分选效果的好坏与矿物粒度存有密切的关系，存在一个合适的粒度分选范围。

图15　石英矿各粒度分选收集率Fig.15　Cumulative weight distribution of Quartz

那是不是矿物颗粒粒度越大，其运动轨迹向内聚拢现象越明显，分选效果越好呢？其实不然，以粒度为150 μm、200 μm、250 μm、300 μm、400 μm的硫铁矿进行分选轨迹模拟为例，模拟结果如图16所示。

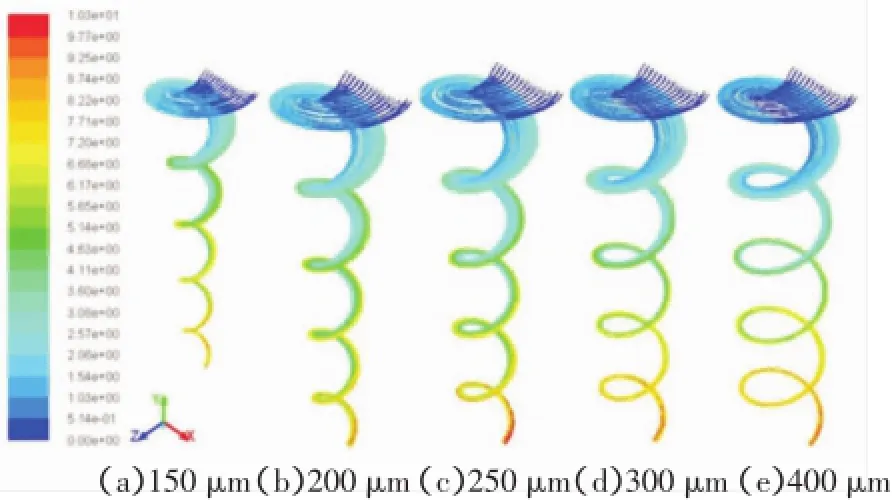
图16　硫铁矿在较大粒度下的轨迹模拟结果Fig.16　Pyrite trajectory simulation results at a larger granularity

图16中可以看出矿物颗粒随着粒度的增加，并不会越来越向槽内缘聚拢，反而有颗粒运动轨迹半径会增加，向槽外缘扩散的现象发生。这是因为随着粒度的增大，颗粒受到的水流影响会加剧，颗粒受到朝向外缘的离心力影响大于朝向内缘的重力分力，造成颗粒随着径向水流向外缘方向运动，远离了槽内缘。

为方便直观研究分析，选出两组硫铁矿粒度（150 μm、400 μm）进行单独对比分析，如图17所示。由图17可以更为明显地看出区别，粒度150 μm的两个硫铁矿颗粒在经过2.5圈（7 s），运动半径不断减小，逐渐向半径为0.05 m的内缘接近。2.5圈以后，颗粒已经基本稳定下来，以运动半径为0.05 m紧贴着槽内缘运动，最后在10 s左右完成了整个分选过程。而粒度为400 μm的硫铁矿向内靠拢运动不明显，只在2圈约6 s的时间内，运动半径减小了0.15 m，相比粒度150 μm的颗粒运动半径约缩减0.25m而言，相差了10cm，这对分选结果是不利的。

图17　不同粒度的硫铁矿颗粒运动轨迹曲线Fig.17　Pyrite particle trajectory curve with different particle size

所以一般BL600螺旋溜槽适宜的分选粒度范围在20 μm到200 μm之间。

从图16中还可以得出一些信息，粒度为400μm的矿粒由于粒度增大，受到径向水流的作用更加明显，在0～2 s拥有比150 μm粒度颗粒更大的斜率，运动速度会比小粒度的颗粒更大，但由于大粒度颗粒的稳定后的运动半径比小粒度颗粒大10 cm，所以造成了粒度400 μm硫铁矿颗粒完成整个分选过程时间比粒度150 μm矿粒多出了2.5 s。

模拟结果的分析与生产实践及理论研究都是相一致的，即同种密度颗粒，细颗粒聚集在内缘，粗颗粒聚集在外缘，粒度更细的矿泥则会聚集在最外缘。证明了该FLUENT数值模拟方法的可行性。

3　结论

本文确定了BL600螺旋溜槽分选流场计算域并建立其矿物分选CFD模型，对矿物颗粒在整个分选过程中的运动轨迹进行了离散相轨迹仿真，揭示了螺旋溜槽设备重选分选的原理。着重分析了在分选流场中不同比重、粒度矿物颗粒的运动轨迹，很好地阐明了螺旋溜槽分选流场中矿物颗粒运动轨迹规律，此模型的建立也为今后螺旋溜槽结构改进优化提供了可行有效的方法。

［1］彭会清，李广，胡海洋，等.螺旋溜槽的研究现状及展望［J］.有色金属科学与工程，2009（3）：26-29.

PENG Huiqing，LI Guang，HU Haiyang，et al.Research status and prospect of spiral chute［J］.Jiangxi Nonferrous Metals，2009（3）：26-29.

［2］曾安，周源，余新阳，等.重力选矿的研究现状与思考［J］.中国钨业，2015，30（4）：42-47.

ZENG An，ZHOU Yuan，YU Xinyang，et al.Research status and thinking of gravity concentration［J］.China Tungsten Industry，2015，30（4）：42-47.

［3］MAHRAN G M A，DOHEIM M A，ABU-ALI M H，et al.CFD simulationofparticulateflowinaspiralconcentrator［J］. Materialprufung，2015，57（9）：811-816.

［4］高淑玲，魏德洲，崔宝玉，等.基于CFD的螺旋溜槽流场及颗粒运动行为数值模拟［J］.金属矿山，2014，32（11）：121-126.

GAOShuling，WEIDezhou，CUIBaoyu，etal.CFD-based numerical simulation of flow field and the particle movement of spiral chute［J］.Metal Mine，2014，32（11）：121-126.

［5］李斌，刘学海.多段螺旋溜槽回收钛的试验研究［J］.金属矿山，1998（3）：23-24.

LI Bin，LIU Xuehai.Experimental study on multi section spiral chute recovery of titanium［J］.Metal Mine，1998（3）：23-24.

［6］刘惠中，李华梁，格海超.BL1500螺旋溜槽在承德某铁矿铁精矿再选中的应用［J］.有色金属工程，2016，6（1）：45-48.

LIUHuizhong，LIHualiang，GEHaichao.Applicationand reselection of BL1500 spiral chute in Chengde iron ore［J］. Nonferrous Metals Engineering，2016，6（1）：45-48.

［7］CHATTOPADHYAY K，ISAC M，GUTHRIE R I L.Considerations in using the discrete phase model（DPM）［J］.Steel Research International，2011，82（11）：1287-1289.

［8］MAHRAN G M A，DOHEIM M A，ABU-ALI M H，et al.CFD simulationofparticulateflowinaspiralconcentrator［J］. Materialprufung，2015，57（9）：811-816.

［9］DOHEIM M A，GAWAD A F A，MAHRAN G M A，et al.Numerical simulation of particulate flow in spiral separators:Part I，low solids concentration（0.3&3%Solids）［J］.Applied Mathematical Modelling，2013，37（1/2）：198-215.

Mineral Particles Trajectory of Spiral Concentrator Separating Flow Field

LIU Zuoshi1，ZHAO Nanqi1，LIU Huizhong1，2，LI Hualiang1
（1.School of Mechanical and Electrical Engineering，Jiangxi University of Science and Technology，Ganzhou 341000，Jiangxi，China；2.Beijing General Research Institute of Mining and Metallurgy，Beijing 100160，China）

Based on BL600 spiral chute which was developed by BGRIMM，this paper studies the discrete phase particle trajectory by applying the multiphase flow field and establishing the spiral concentrator separation CFD model.The separation process is compared with the simulation results with already existing separation mechanism. The results proved the reliability of the CFD model and demonstrated the spiral concentrator gravity separation principle.It provided a research platform of numerical simulation for improvement and optimization of the spiral groove structure.

spiral concentrator；CFD model；separation process；particle trajectory

TD455

A

10.3969/j.issn.1009-0622.2016.05.013

2016-06-05

国家自然科学基金（71361014）；江西省重点科技计划项目（20151BBE50038）

刘祚时（1963-），男，江西永新人，教授，本刊编委，主要从事矿山设备自动化、智能机器人技术。