一种基于相关系数的目标角度估计算法

代培龙

(南京电子技术研究所,南京 210039)



一种基于相关系数的目标角度估计算法

代培龙

(南京电子技术研究所,南京 210039)

实际应用的波达角估计算法主要有最大似然估计、比幅和超分辨等。文中在深入分析这些算法的基础上，提出了一种新的角度估计算法，称之为相关角度估计算法。理论研究和仿真分析表明：相关角度估计算法更易于工程化，相对于比幅法有更高的角度估计精度，比最大似然估计具有更小的计算量，比超分辨测角估计更高，计算量更小。

最大似然估计；比幅测角；超分辨测角；相关系数；阵列扫描

0 引 言

角度估计是阵列信号处理的研究热点，在雷达、声纳、通信和医学成像等领域有着广泛应用，一直是雷达探测的重要功能，因此，精确角度估计是雷达信号处理的重要环节[1]。目前阵列信号处理角度估计常见的算法包括：最大似然估计、比幅度测角和超分辨测角法等。

最大似然估计一般不是无偏的，但其偏差可以通过对估计值乘某合适的常数加以消除，角度估计精度高，然而这类方法通常需要全局极值搜索，计算量无法满足实时处理。比幅测角法把空间合成几个波束，通过比幅得到目标角度信息，比幅法能有效地降低运算量，但信噪比损失较大，测角精度差。超分辨方法是一种实际可行的次优估计方法，角度估计精度高，不过这类算法通常具有较高的信噪比门限并需要较多的采样快拍，同时特征值分解的运算量仍然很大[2-3]。

目前雷达工程应用中主要采用最大似然法，比幅测角法和超分辨测角方法由于计算量和测角精度的影响，在工程上应用较少。本文借鉴文献[4-5]中基于相关法测频的思想，提出了一种相关测角算法，并且对算法搜索过程进行了优化，从而大大降低了计算量。

1 信号模型

设L个目标回波信号入射到N单元天线线阵，如图1所示，N单元线阵接收信号可表示为

X(t)=As(t)

(1)

式中：s(t)=[s1(t),s2(t),…,sL(t)]T为信号矢量；A=[a(θ1),a(θ2),…,a(θL)]。

其中

a(θi)=[1,exp(φi),…,exp(N-1)φi]

(2)

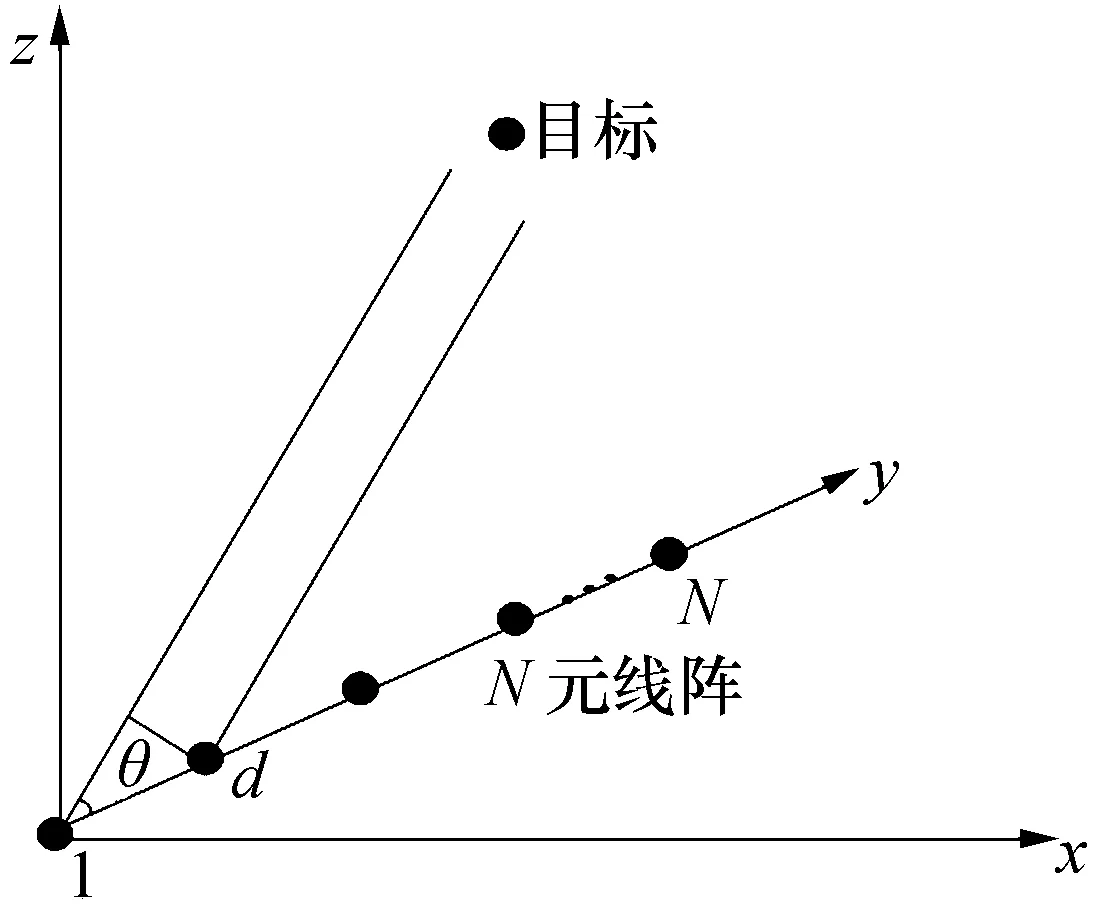
图1 N单元等距线阵

2 现有波达角估计算法

2.1 最大似然估计法

将各阵元的输出进行加权求和，天线阵列的波束“导向”到一定方向上

y(tθ)=WHX(t)=s(t)WHa(θ)

(3)

式中：W为期望波达方向矢量，假设期望波达方向为θ0，则W=[ω0,ω1,…,ωN-1]，其中

(4)

数字阵列对一定方向进行加权求和得到观测样本，最大似然估计可记为

(5)

2.2 比幅测角法

比幅测角法采用两个参数相同的和波束进行波束交叠[8-9]，或者采用和差波束测角，本文分析和波束测角，两和波束交叠对应的方位为θ0，两波束中心方位角度为θ1和θ2。如图2所示，假设两个相互重叠的波束回波信号为

(6)

式中：f(θ1)、f(θ2)为方向函数，通过对u1和u2进行幅度比值处理，在预先得到的幅度-方位表中查找该值对应的角度修正值，即是目标角度。

2.3 超分辨测角法

经典的超分辨算法包括：music多重信号分类算法算法、esprit算法等，本文主要针对music算法和本文算法分析比较，music算法的基本思想是对天线阵列接收的数据协方差进行特征值分解，将特征值划分为相互正交的子空间，一个为信号子空间，一个为噪声子空间，然后，利用两个子空间的正交性来生成空间扫描谱函数，通过搜索谱峰位置来获得信号的波达方向[10-11]。

图2 双波束比幅

对于空间的信源，接收阵列表示为

X(t)=As(t)+N(t)

(7)

式中：A为方向矩阵；s(t)为入射信号矢量；N(t)=[n1(t),n2(t),…,nN(t)]为噪声矢量。

通过对协方差矩阵的分解，利用信号方向矢量与噪声特征向量正交，则music空间谱估计可记为

(8)

峰值对应着整列上得到达角。

3 相关角度估计算法

3.1 算法原理

根据式(3)，阵列信号在θ0方向的离散响应为

y(nθ0)=s(n)WHa(θ)

(9)

把式(9)写成幅相分量形式

(10)

由sad(·)函数性质可知，式(10)中只有θ=θ0-dθ,θ0,θ0+dθ三个方位角度在目标回波包络的主瓣内，可近似表示为

y(nθ1)≈[Pθ0-dθ·δ(θ-θ0+dθ)+Pθ0·

δ(θ-θ0)+Pθ0+dθ·δ(θ-θ0dθ)]

(11)

式中：δ(·)为狄拉克函数，函数Pθ0可表示为

(12)

可知在采样样本数N固定的情况下，复数Pθ0-dθ、Pθ0、Pθ0+dθ，由dθ唯一确定。

由以上分析角度估计问题实际上就是估计θ0和dθ，称θ0为粗估计值，参数dθ为微估计值。粗估计值由精度较低的比幅测角直接给出。

接下来分析dθ的估计方法，将原空间采样间隔Δθ等分成K份，则每一个微刻度唯一对应了一组[Pθ0-dθ,Pθ0,Pθ0+dθ]，K个空间刻度，对应了K组复向量，称

Pk=[Pθ0-dθ(k),Pθ0(k)，Pθ0+dθ(k)]

(13)

式中：k=1,2,…,K，Pk为估计原始样本，这些原始样本确定了所有可能的dθ。

相关系数即

(14)

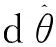
(15)

3.2 算法计算量优化

相关算法中微估计值需要做k次相关运算才能遍历原始样本，得到微估计值dθ。由于P与原始样本的相关系数有唯一最大值，在最大值两边具有单调减的性质，如图3所示。

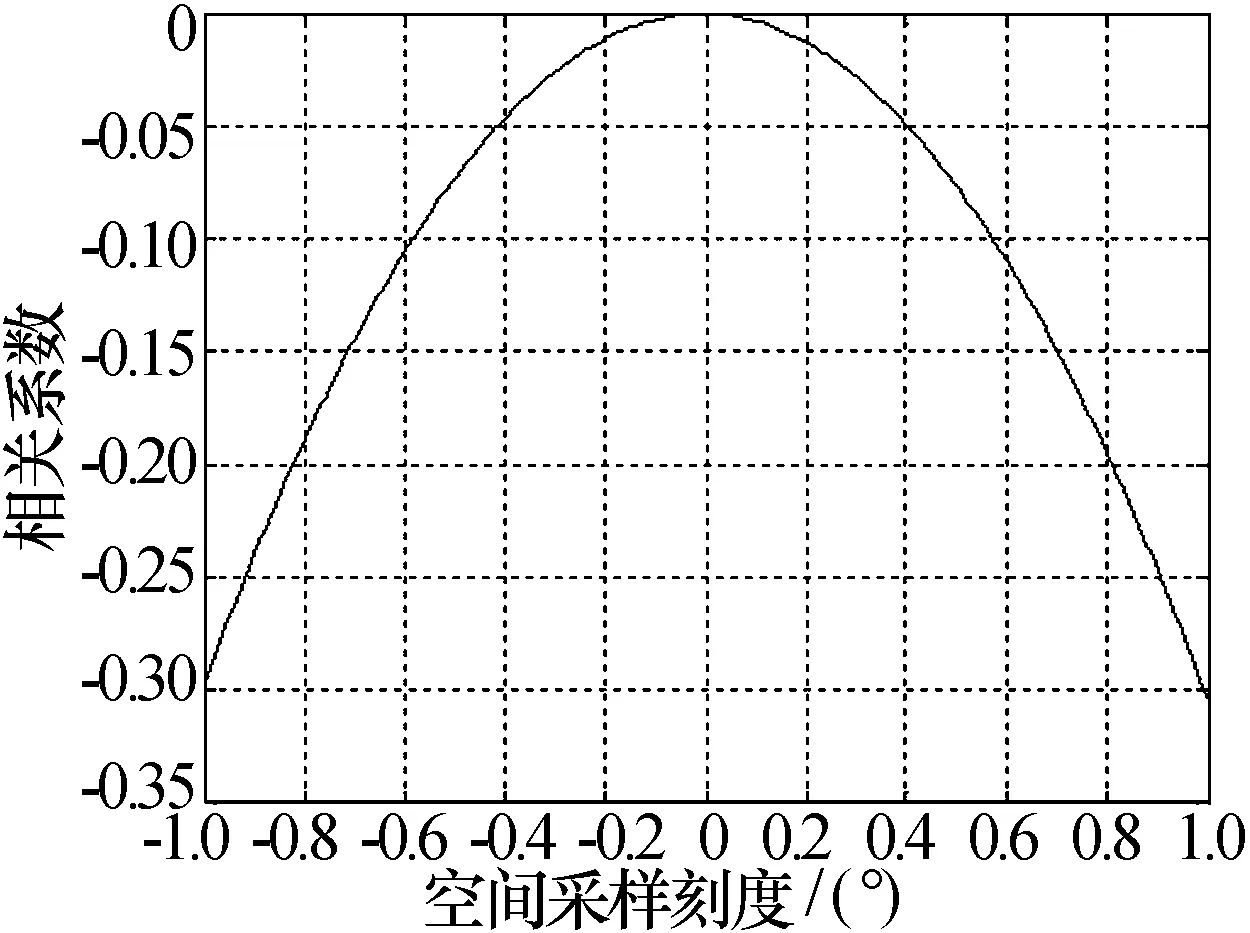
图3 粗估计与微估计样本的相关系数

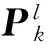
4 仿真分析

对阵列单元数为16，单元间距半波长线阵进行最大似然估计法、比幅测角法、相关法和超分辨方法测角仿真分析，由理论分析算法流程可知最大似然 法计算量为M次16点的乘加运算，M取决于波束形成的角度刻度，即样本数；比幅测角法计算量为M次的16点乘加运算，M取决于波束形成的个数，本仿真在-20°～20°范围内取9个波束；超分辨测角计算量取决于做16×M点的特征值分解，M为每单元采样点数；优化后的相关法主要计算量则为M次16点的乘加运算和⎣lb(K)」+1次3点乘加运算。通过计算量分析最大似然法计算量最大，然后分别是超分辨方法和相关法，比幅法计算量最小。

对上述几种估计算法精度进行仿真比较，蒙特卡罗仿真次数为1 000次。图4给出了四种估计在不同信噪比下的均方根误差。

图4 估计算法均方根误差比对图

从图中可看出在高信噪比下最大似然估计误差最好，相关法估计误差为最大似然估计误差的1.02倍，比幅测角估计误差为最大似然估计的3.60倍，超分辨法为最大似然的1.31倍，四种算法的性能比较如表1所示。

表1 算法性能比较

注：表中的比较相对于最大似然估计。

5 结束语

针对最大似然估计和超分辨测角计算量大，比幅测角虽然计算量小，但测角精度低的特点，本文提出一种基于相关系数的角度估计算法，并对算法进行了优化，减少了计算量。仿真分析表明：当信噪比较大时，本文提出的算法估计误差接近最大似然估计法，是最大似然估计法误差的1.02倍，但是计算量大大降低；相对于超分辨法计算量小，但测角精度更高；相对于比幅法计算量大，但测角精度有很大提升，比幅测角误差为相关法的3.5倍，相关法避免了比幅法的信噪比损失。从计算量上考虑，相关法测角比最大似然法和超分辨法更容易工程化实现。

[1] TSHBAN C.Highlights of statistical signal and array pocessing[J]．IEEE Signal Processing Magazine，1998，16(5)：21-64.

[2] 吴顺君,梅晓春．雷达信号处理和数据处理技术[M]．北京:电子工业出版社，2008．

WU Shunjun，MEI Xiaochun．Radar signal processing and data processing technique[M]．Beijing:Publishing House of Electronics Industry，2008．

[3] FORSTER P,LARZABAL P,BOYER E.Threshold performance analysis of maximum likelihood DOA estimation[J].IEEE Transactions on Signal Processing,2004,52(11):3183-3191.

[4] 蒋 为.一种基于相关系数的频率估计算法[J].微波学报,2012,28(2):49-52.

JIANG Wei.Algorithm of frequency estimation based on correlation coefficient[J].Journal of Microwaves，2012，28(2)：49-52.

[5] 张二伟,肖文书.一种基于相关系数的距离估计算法[J].现代雷达,2014,36(11):58-61.

ZHANG Erwei，XIAO Wenshu.Algorithm of range estimation based on correlation coefficient[J].Modern Radar,2014,36(11):58-61.

[6] 杨雪亚,陈伯孝.一种新的二维角度估计的高分辨算法[J].电子信息学报，2010,32(4):953-958.

YANG Xueya,CHEN Baixiao.High-resolution method for 2D DOA estimation[J].Journal of Electronics & Information Technology,2010,32(4):953-958.

[7] 郑春弟.基于非圆信号的空间谱估计算法研究[D].西安:西安电子科技大学,2006.ZHENG Chundi.Estimation algorithm in spatial spectrum based on noncircular signals[D].Xi′an:Xidian University,2006.

[8] 王成海.雷达测角方法研究[D].西安:西安电子科技大学,2013.

WANG Chenghai .The research of radar angular measurement methods[D].Xi′an:Xidan University,2013.

[9] 丁鹭飞，耿富录，陈建春.雷达原理[M].北京：电子工业出版社,2009.DING Lufei，GENG Fulu，CHEN Jianchun.Principles of radar[M].Beijing：Publishing House of Electronics Industry，2009.

[10] 董晓辉，柯亨玉，董志飞.阵列误差对四阶MUSIC算法到达角估计的影响[J].现代雷达,2005,27(1):41-43.

DONG Xiaohui,KE Hengyu,DONG Zhifei.An analysis of FO-MUSIC algorithm in the presence of sensor perturbations[J].Modern Radar,2005,27(1):41-43.

[11] 童宁宁,郭艺夺,王光明.米波雷达低角跟踪环境下的修正MUSIC算法[J].现代雷达,2008,30(10):29- 32.TONG Ningning,GUO Yiduo,WANG Guangming.Modified MUSIC algorithm in meter-band radar low-angle tracking environment[J].Modern Radar,2008,30(10):29- 32.

代培龙 男，1984年生，硕士，工程师。研究方向为雷达系统设计、雷达信号处理。

Algorithm of Angle Estimation Based on Correlation Coefficient

DAI Peilong

(Nanjing Research Institute of Electronics Technology,Nanjing 210039,China)

At present,the actual application of the DOA estimation algorithms includes maximum likelihood estimation,amplitude angle measurement,super-resolution angle measurement and etc.On the basis of an in-depth analysis on these algorithms,this paper proposes a new angle estimation algorithm,which is called the correlation angle algorithm.Theoretical researches and simulation analyses show that the correlation angle algorithm is easier for engineering,more accurate than amplitude angle measurement and less complex in calculation than maximum likelihood estimation.in addition,compared with super resolution angle measurement,it is higher in the estimated value and smaller in the amount of calculation.

maximum likelihood estimate; amplitude angle; super-resolution angle measurement; correlation angle algorithm; array scanning

��处理·

10.16592/j.cnki.1004-7859.2016.10.007

代培龙 Email：longdpl@126.com

2016-07-08

2016-09-21

TN957.51

A

1004-7859(2016)10-0029-03