基于改进人工蜂群算法的漏磁缺陷轮廓重构*

韩文花，汪胜兵，王建，吴正阳，王平

（1.上海电力学院自动化工程学院，上海200090；2.南京航空航天大学自动化学院，南京210016）

基于改进人工蜂群算法的漏磁缺陷轮廓重构*

韩文花1，汪胜兵1，王建1，吴正阳1，王平2

（1.上海电力学院自动化工程学院，上海200090；2.南京航空航天大学自动化学院，南京210016）

漏磁缺陷重构是指由检测到的漏磁信号重构缺陷轮廓及参数，是实现漏磁反演的关键。将局部最优解和全局最优解引入到人工蜂群算法（Artificial Bee Colony Algorithm，ABC）中，提出了一种基于改进人工蜂群算法的缺陷重构模型。在该模型中，径向基函数神经网络作为前向模型求解漏磁信号，改进人工蜂群算法用于求解反演问题中的优化问题。将改进人工蜂群算法和基本人工蜂群算法作为反演算法进行了比较，实验结果表明，改进人工蜂群反演算法精度较高，速度较快，同时对实测信号具有鲁棒性，是一种有效可行的漏磁反演新方法。

人工蜂群算法，漏磁信号，缺陷轮廓

0　引言

漏磁检测是铁磁材料常用的无损检测方法之一，具有原理简单、在线检测能力强、不受材料表面油污及其他非导磁覆盖物影响等优点［1］。漏磁检测包括正演和反演两个方面，漏磁缺陷轮廓重构是指由检测到的漏磁信号重构缺陷轮廓或几何参数，是进行漏磁检测与评估的关键［1-2］。目前国内外对漏磁反演问题的研究主要有神经网络法［3-5］和优化方法［6-8］。神经网络具有非线性映射和自学习能力，能实现输入漏磁信号和输出裂纹形状非线性关系的逼近。但是神经网络法对训练样本依赖性大，且对噪声敏感。优化法是建立一个目标函数，通过各种优化算法使目标函数的值最小，因此，合适的优化算法是优化方法反演的关键。

土耳其埃尔吉耶斯大学的Karaboga受自然界蜜蜂觅食过程中蜂群个体之间的劳动分工和自组织行为的启发，于2005年首次提出基于蜂群觅食行为的人工蜂群（Artificial Bee Colony，ABC）算法［9］。ABC算法原理比较简单，预设参数少，而且算法相对于其他已知的优化算法能够较好地平衡优化过程中的局部寻优和全局寻优能力，在一定程度上减小了陷入局部最优的可能性，提高了算法整体的寻优能力，已经快速成为优化领域中强有力的全局优化工具之一［10-11］。本文将ABC算法作为反演算法用于漏磁重构，以实现快速、准确的漏磁反演。

1　基于改进ABC算法的漏磁缺陷轮廓模型

1.1改进的ABC算法

在基本ABC算法［12］中，将人工蜂群按分工分为3种:采蜜蜂、观察蜂和侦察蜂。其中，采蜜蜂和观察蜂各占一半，并且每一个蜜源仅有一个采蜜蜂工作，即采蜜蜂的数量与蜜源数量相等，用FN表示。算法初始化时按式（1）随机生成FN个D维初始解并对每个蜜源按式（2）计算对应的适应度值。其中，rand为［0，1］的随机值，搜索过程如下:

1）采蜜蜂阶段:在每个蜜源的邻域附近实施局部搜索，根据搜索结果的好坏判断是否需要更新蜜源；

2）观察蜂阶段:根据蜜源适应度值的大小，观察蜂选取适应度值较大的蜜源，转变为采蜜蜂继续执行上述搜索更新过程；

3）侦察蜂阶段:从所有蜜源中淘汰一个含蜜量即将殆尽的蜜源（或者说该蜜源经过多次搜索其适应度值仍无法提高），进而对应的采蜜蜂转为侦察蜂，继续随机地在整个搜索空间中选择新的潜在优质蜜源。

通过以上过程蜂群开始进行搜索，算法中的每个蜜源代表优化问题中的一个可能解，蜜源的质量对应着解的质量，用适应度值fitness表示:

其中f（xi）表示对应问题的目标函数值。每个采蜜蜂在其蜜源邻域附近搜索公式为:

其中t为当前迭代次数；j∈｛1，2，…，D｝，k∈｛1，2，…，FN｝，j、k为其值域内的随机取值，且k≠j；φ∈［-1，1］为服从均匀分布的随机数。采蜜蜂完成搜索后，观察蜂以轮盘赌的方式选择一个蜜源:

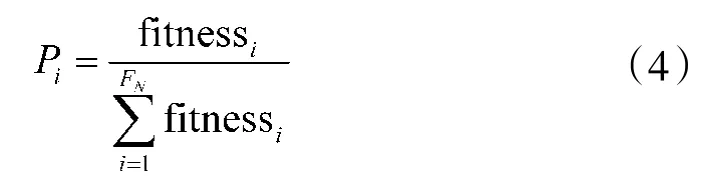
Pi值越大的蜜源能吸引更多的观察蜂前往采蜜，在“被招募”之后，观察蜂转变为采蜜蜂，采用式（3）所示的局部搜索策略进行开采。当一个蜜源在采蜜蜂和观察蜂阶段经过一定次数开采之后，其解的质量仍得不到改进，该蜜源将被抛弃，进而根据式（1）随机选取新的蜜源，用limit表示允许开采的最大次数。

为了克服基本ABC算法容易陷入局部最优解的缺点，胡珂等提出了一种改进的ABC算法［13］，虽然一定程度上解决了容易陷入局部最优的问题，但使得算法的收敛速度变慢。在此基础上本文引入当前最优解pbest和全局最优解gbest用来加快算法收敛速度。改进ABC算法的采蜜蜂和观察蜂的邻域搜索公式分别为式（5）、式（6）。

以上两式中的j、k和φ的取值方式与式（3）相同。改进后算法步骤如下:

步骤1:设置初始参数，按照式（1）得到初始解，按式（2）计算适应度fitness值，并计算当前最优解pbesti和全局最优解gbest的值；

步骤2:采蜜蜂按式（5）搜索蜜源计算fitness，若蜜源质量变好，则更新采蜜蜂当前位置、pbesti和gbest的值并将计数变量counteri置0，否则采蜜蜂当前位置不变将counteri加1；

步骤3:计算Pi，若Pi大于一个随机值，则观察蜂转化为采蜜蜂，按照式（6）搜索蜜源计算fitness，若蜜源质量变好更新采蜜蜂当前位置、pbesti和gbest的值并将计数变量counteri置0，否则，采蜜蜂当前位置不变，并将counteri加1；

步骤4:若counteri＞limit，则抛弃该蜜源，按式（1）选取新蜜源；

步骤5:若达到最大迭代次数，输出结果；否则返回步骤2，进入下一次迭代。

1.2缺陷轮廓重构模型

基于改进ABC算法的漏磁缺陷轮廓方法中，通过径向基函数神经网络（radial-basis function neural network，RBFNN）前向模型来预测缺陷的漏磁信号。以测量的漏磁信号与RBFNN预测的漏磁信号间的均方误差为目标函数，用改进的ABC算法进行迭代，得出最终轮廓。目标函数为:

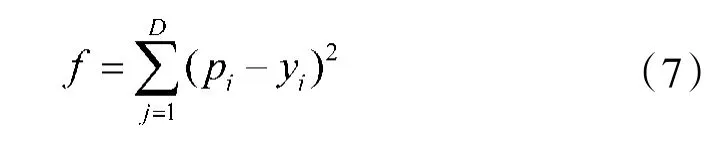
式中D为漏磁信号的维度，P=［p1，p2，…，pD］是实测漏磁信号，Y=［y1，y2，…，yD］是RBFNN预测的漏磁信号。缺陷轮廓重构原理框图如图1所示。

图1　缺陷轮廓重构原理框图

2　实验结果

为了验证基于ABC反演算法的有效性，使用了240个不同缺陷的漏磁信号二维仿真数据。在240个缺陷轮廓和漏磁信号数据对中，210个用于训练神经网络，30个用作测试数据库。实验中，RBFNN有100个输入节点和100个输出节点，并且利用正交最小二乘算法训练RBFNN。图2是宽7.62 cm、深0.889 cm，钢板厚度2.54 cm的缺陷的轮廓和漏磁信号。

图2　缺陷轮廓（a）和对应的漏磁信号（b）

将蜂群数量设为100（采蜜蜂和观察蜂数量分别为50），limit值为100，解空间范围为［-2.159，0.254］cm，改进ABC算法最大迭代次数为5 000，基本ABC算法最大迭代次数为10 000。图3～图6为基于改进ABC和基本ABC的缺陷重构仿真结果，图中实线为缺陷的真实轮廓，虚线为基于基本ABC算法的重构轮廓，点划线为基于改进ABC算法的重构轮廓。表1为基于基本ABC算法和改进ABC算法的反演方法目标函数终值和计算时间。

图3　宽6.604 cm，深0.889 cm的缺陷轮廓反演

图4　宽6.604 cm，深1.905 cm的缺陷轮廓反演

图5　宽8.636 cm，深2.159 cm的缺陷轮廓反演

图6　宽10.668 cm，深0.381 cm的缺陷轮廓反演

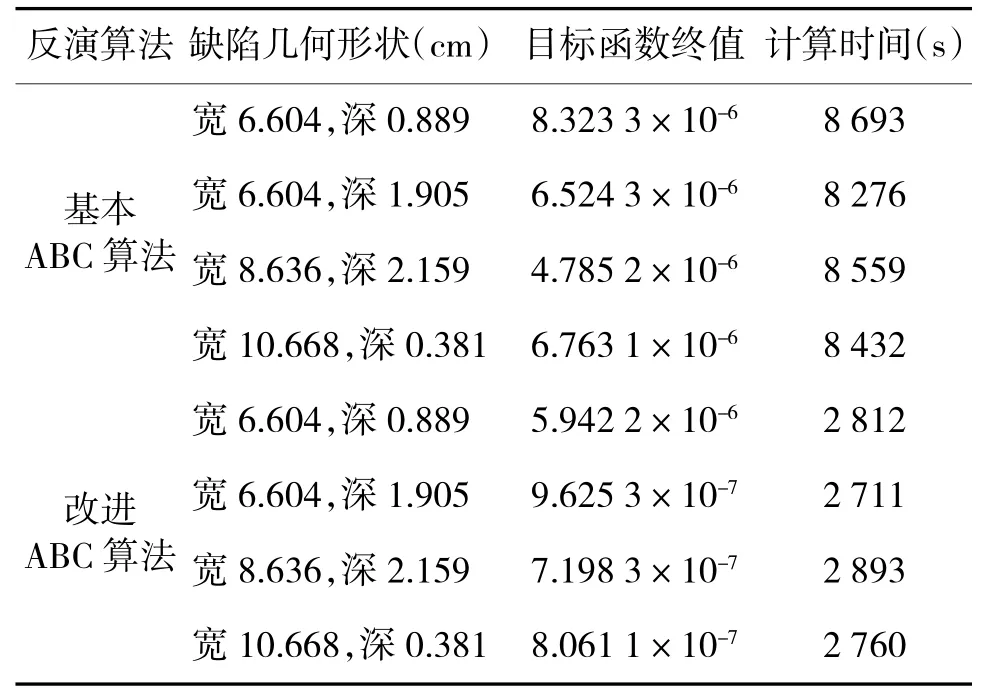
表1　目标函数终值和计算时间

从图3～图6可以看出，基于改进的ABC算法的重构效果要比基于基本ABC算法好得多，但缺陷的宽度和深度对重构的效果影响很大，较深和较宽的缺陷重构的效果要好；由表1可以看出，基于改进ABC算法的迭代次数是基于基本ABC算法的一半，所以前者的计算时间明显比后者短，从目标函数的最终值也可以看出，前者要比后者效果好。

为了验证所提反演算法对实测漏磁信号的可行性，采用如下页图7所示的装置进行实测漏磁信号的采集。

实测装置中，转盘直径为0.849 4 m，不同缺陷刻在了转盘的外周。励磁电流为0.87 A，数据采样频率为120 kHz，传感器提离值为1 mm。依然用训练好的RBFNN为前向模型，ABC算法参数设置不变，图8与图9为不同缺陷的实测信号反演结果，图中实线为缺陷的真实轮廓，虚线为基本ABC算法重构轮廓，点划线为改进ABC算法重构轮廓。表2为目标函数最终值和计算时间。

图8　宽1.942 cm，深0.666 cm的缺陷轮廓反演

图9　宽1.942 cm，深1.448 cm的缺陷轮廓反演

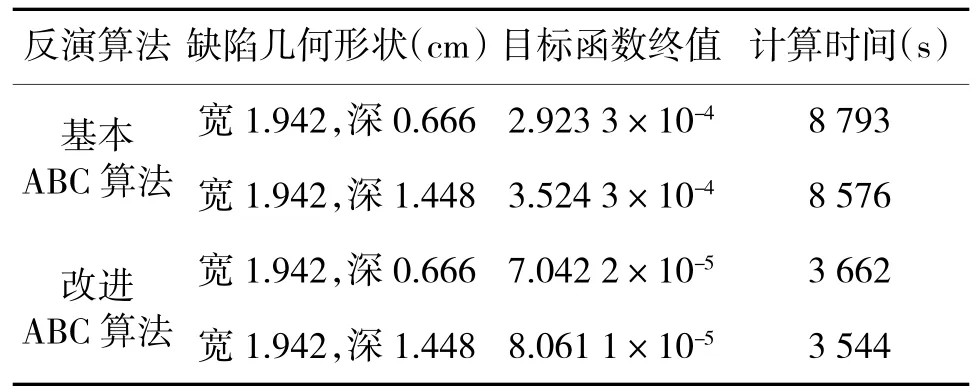
表2　目标函数终值和计算时间

从图8与图9中可以看出基于改进ABC算法的漏磁反演方法对实测信号也能较准确地重构出缺陷轮廓。在相同迭代次数下表2中的目标函数最终值比表1中的大，这是因为实测信号中包含实验装置及环境产生的噪声，所以精度有所降低。

3　结论

本文引入了一种改进的人工蜂群算法，并将其用于漏磁缺陷轮廓重构。实验结果表明，基于改进人工蜂群算法的漏磁反演方法比基于基本人工蜂群算法的反演精度高，需要时间短，而且对实测信号具有一定的鲁棒性，是一种有效可行的漏磁反演新方法。

［1］SNARSKII A A，ZHENIROVSKYY M，MEINERT D，et al. An integral equation model for the magnetic flux leakage method［J］.NDT&E International，2010，43:343-347.

［2］苑希超，王长龙，王建斌.基于贝叶斯估计的漏磁缺陷轮廓重构方法研究［J］.兵工学报，2012，33（1）:138-141.

［3］XU C，WANG C L，JI E Z，et al.Finite-element neural network-based solving 3-D differential equations in MFL［J］. IEEE Transactions on Magnetics，2012，48（12）:4747-4756.

［4］CARVALHOA A A，REBELLOA J M A，SAGRILO L V S. MFL signals and artificial neural networks applied to detection and classification of pipe weld defects［J］.NDT&E International，2006，39:661-667.

［5］雷良金，王长龙，孙世宇，等.基于蚁群算法的径向基网络漏磁信号二维反演［J］.火力与指挥控制，2011，36（3）: 163-165.

［6］HAN W H，XU J，WANG P，et al.Defect profile estimation from magnetic flux leakage signal via efficient managing particle swarm optimization［J］.Sensors，2014，14:10361-10380.

［7］刘美全，徐章遂，王建斌.基于磁偶极子能级分布的缺陷反演成像［J］.中国机械工程，2005，16（11）:952-955.

［8］韩文花，徐俊，沈晓晖，等.自学习粒子群与梯度下降混杂的漏磁反演方法［J］.火力与指挥控制，2015，40（1）: 88-91.

［9］KARABOGA D.An idea based on honey bee swarm for numerical optimization［R］.Technical Report-tr06，Erciyes U-niversity，Engineering Faculty，Computer Engineering Department，2005.

［10］PARK J，HAN Y.Swarm intelligence topology optimization based on artificial bee colony algorithm［J］.International JournalofPrecisionEngineeringandManufacturing，2013，14（1）:115-121.

［11］BANSAL J C，SHARMA H，ARYA K V.Memetic search in artificial bee colony algorithm［J］.Soft Computing，2013，17（10）:1911-1928.

［12］邱剑锋，谢娟，汪继文.基于交叉突变算子的人工蜂群算法及其应用［J］.计算机应用研究，2014，31（5）: 1336-1341.

［13］胡珂，李迅波，王振林.改进的人工蜂群算法性能［J］.计算机应用，2011，31（4）:1107-1110.

Profiles Reconstruction of Magnetic Flux Leakage Based on Improved Artificial Bee Colony Algorithm

HAN Wen-hua1，WANG Sheng-bing1，WANG Jian1，WU Zheng-yang1，WANG Ping2
（1.College of Automation Engineering，Shanghai University of Electric Power，Shanghai 200090，China；2.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

The reconstruction of magnetic flux leakage（MFL）defect profiles means the reconstruction of defect profiles and parameters from MFL inspection signals.It is the key for the inversion of MFL inspection signals.The local optimal solution and the global optimal solution have been introduced into the artificial bee colony algorithm，and a kind of defect reconstruction model based on improved artificial bee colony algorithm is proposed.In the model，radial-basis function neural network is utilized as forward model，and the improved artificial bee colony algorithm is used to solve the optimization problem in the inverse problem.The comparison between basic artificial bee colony algorithm and proposed improved artificial bee colony algorithm which indicate that the proposed method has high accuracy and robustness against the real measure signals，and it is an effective and feasible approach for solving inverse problems

artificial bee colony algorithm，magnetic flux leakage signal，defect profile

TP301.6

A

1002-0640（2016）06-0015-04

2015-05-06

2015-06-07

国家自然科学基金（51107080，61304134，61503237）；上海市电站自动化技术重点实验室（13DZ2273800）；上海市重点科技攻关计划项目（14110500700）

韩文花（1976-），山东日照人，女，博士，副教授。研究方向：无损检测、漏磁反演、智能优化算法等。