权重信息不完全的机载雷达作战效能评估模型

张忠

（中国西南电子技术研究所航空电子信息系统技术重点实验室，成都610036）

权重信息不完全的机载雷达作战效能评估模型

张忠

（中国西南电子技术研究所航空电子信息系统技术重点实验室，成都610036）

为解决指标权重信息不完全时的机载雷达作战效能评估问题，提出了一种评估模型。对专家关于指标权重给出的残缺判断矩阵，给出了其一致性评判标准。结合残缺判断矩阵的最佳一致性比例，构造了一个单目标优化模型，用于计算指标权重。在此基础上提出了权重信息不完全的机载雷达作战效能评估模型。最后给出一个实例验证了评估模型的有效性。

机载雷达，作战效能，评估模型，残缺判断矩阵

0　引言

现代战争中，无论进攻方、还是防御方，制空权都是决定胜负的重要条件之一。“先敌发现、先敌发射、先敌命中”的空战理念对机载雷达的性能提出了更高的要求，换言之，机载雷达作为目标探测的重要手段，其作战效能的高低对战斗机制空能力有显著影响。因此，有必要开展机载雷达作战效能评估问题的研究工作。

目前，许多学者提出了不同粒度的机载雷达作战效能评估模型［1-3］。陈世国［4］结合灰色理论，提出了一种机载雷达作战效能评估模型，其所选指标全面且合理，但评估结果极易受主观因素影响。焦广伦［5］分析了影响机载雷达探测性能的主要指标，并针对典型作战场景建立了探测性能评估模型。该模型具有很强的可操作性，但适用范围较窄。唐政［6］提出了机载雷达探测系统效能评估模型，其粒度比较大，只适用于简单的定性分析。

机载雷达作战效能的评估模型必然涉及不同的指标，这就需要确定各个指标的权重。然而，由于空战环境的日益复杂以及敌方武器装备战技术特征的未知性，评估专家很难全面、准确地分析指标相对重要程度，甚至在敏感指标上不愿表明个人偏好。因此，评估专家给出的指标权重信息往往是不完全的，已有的评估模型并不适用此情况。本文结合在残缺判断矩阵方面的研究成果，提出了权重信息不完全的机载雷达作战效能评估模型。

1　相关知识

层次分析法（Analytic Hierarchy Process，AHP）是由美国运筹学家Saaty于20世纪70年代提出的一种定性与定量相结合的决策分析方法。该方法的核心思想是根据决策目标将决策问题逐层分解为一系列相互独立的决策指标，并对专家所给的指标重要度信息进行定量分析，从而获得决策结果。

指标重要度信息是指专家对不同指标的相对重要程度给出的判断，这些判断用数值表示出来（采用九标度法、五标度法等），写成矩阵形式就是判断矩阵。

定义1若矩阵A=（aij）n×n的元素满足:①aij＞0；②aij=1/aji，则称A为正互反判断矩阵，简称判断矩阵。

定义2若判断矩阵A=（aij）n×n的任一元素均满足:

则称A为完全一致判断矩阵。

若判断矩阵是完全一致的，则表明在判断指标相对重要程度时专家的判断完全符合逻辑。然而由于客观事物的复杂性和主观判断的多样性，专家给出的判断矩阵通常是不完全一致的。因此，需要对判断矩阵进行一致性检验，防止过于混乱的判断逻辑引出错误的决策结果。

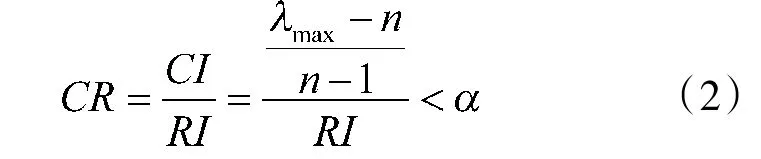
则称A是一致性可接受的。这里α是一致性可接受判断矩阵的临界值，常取α=0.1；CR、CI、RI分别表示判断矩阵的一致性比例、一致性指标、平均随机一致性指标，其中RI的大小与n有关，如表1所示。

表1　平均随机一致性指标

2　作战效能评估模型

2.1指标体系建立

机载雷达的使命任务是在复杂电磁环境下准确地发现目标，快速对目标身份进行识别，并持续跟踪目标以测量目标的位置与状态，为后续火力打击提供目标指示。针对机载雷达的使命任务，可从搜索能力、跟踪能力、识别能力、抗干扰能力等4个方面来衡量机载雷达的作战效能。由此，在遵循指标体系完备性、客观性、可测性等原则［7］的基础上，建立机载雷达作战效能评估指标体系，如下页图1所示。

2.2指标权重确定

作为一种定性与定量相结合的决策分析方法，AHP法具有分析和解决复杂系统问题的简洁性和实用性，因此，本文采用AHP法来确定指标权重。AHP法的关键步骤是由评估专家对不同指标的相对重要程度进行判断，获得判断矩阵。然而，在机载雷达作战效能的评估工作中，评估专家给出的指标权重信息往往是不完整的，换言之，评估专家给出的是残缺判断矩阵。为便于描述，下文均将残缺判断矩阵中的空缺项记为x。

定义4设A是残缺区间判断矩阵，空缺项为xi，i=1，2，…，m。若

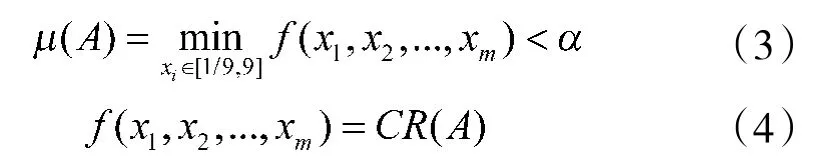
其中，α表示一致性可接受的临界值，则称A是一致性可接受的，且称μ（A）是A的最佳一致性比例。

定理1若判断矩阵A是一致性可接受的，除去A中任意元素，得到残缺判断矩阵A¯，则A¯也是一致性可接受的。

在机载雷达作战效能评估指标体系中，任选一组同父指标集P=｛p1，p2，…，pn｝；参与评估工作的专家组为E=｛e1，e2，…，em｝；专家ek针对指标集P给出的残缺判断矩阵为Ak=，k=1，2，…，m。

在依据残缺判断矩阵确定指标权重时，若残缺判断矩阵是一致性不可接受的，表明相关专家的判断逻辑过于混乱，所给指标权重信息不足信，故应将该残缺判断矩阵摒弃；若残缺判断矩阵是一致性可接受的，其最佳一致性比例越小且残缺元素越少，表明相关专家的判断逻辑越严谨，知识面越广，故应更加重视该残缺判断矩阵。基于上述分析，为确定指标权重向量ω=（ω1，ω2，…，ωn），建立如下单目标优化模型:

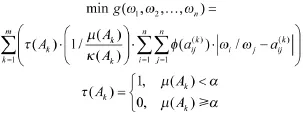
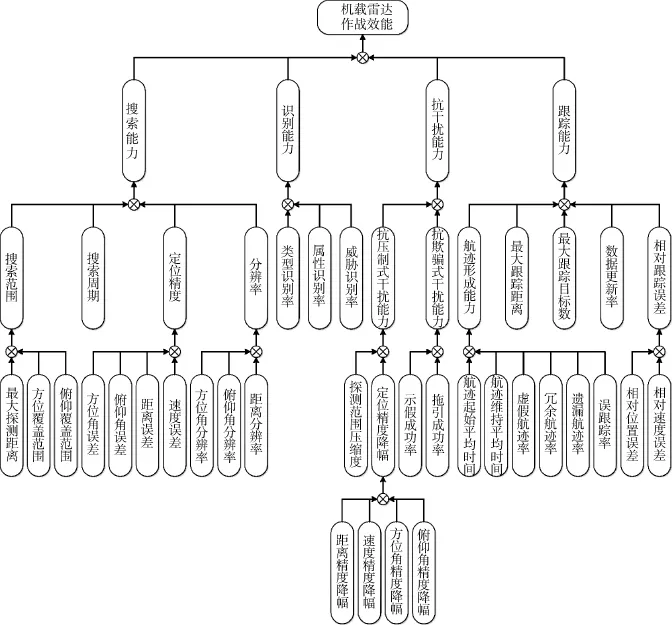
图1　机载雷达作战效能评估指标体系

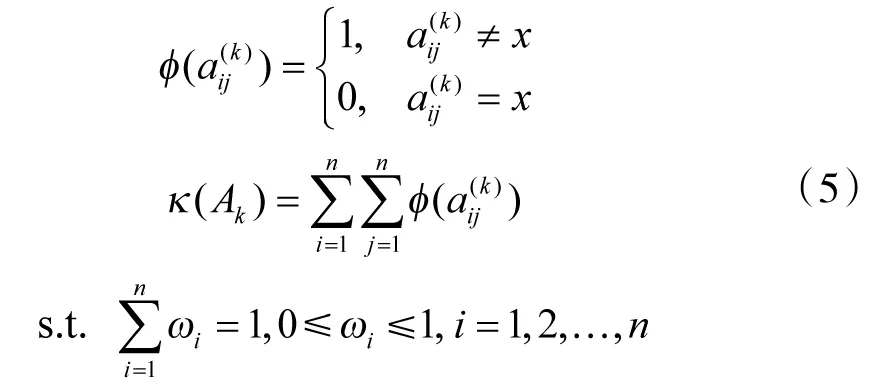
式（5）是一个非线性优化模型，可采用蚁群算法、粒子群算法等对其进行求解，即可得到指标权重向量。

2.3指标功效转换

在机载雷达作战效能评估指标体系中，下层指标为性能指标，上层指标为效能指标。上层指标的效能值是根据下层指标的性能值计算得到的。因此，需要进行性能指标的功效转换，即将机载雷达的性能值转换为机载雷达的效能值。

根据机载雷达作战效能评估的实际情况，本文将性能指标分为以下两类:

①效益型性能指标:指标值越大，表明机载雷达的作战效能越高，例如探测距离；

②成本型性能指标:指标值越小，表明机载雷达的作战效能越高，例如测距误差。

针对机载雷达的效益型性能指标，提出了效益型功效函数，如下所示:

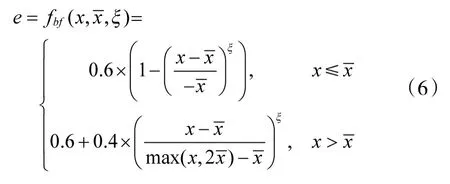
针对机载雷达的成本型性能指标，提出了成本型功效函数，如下所示:

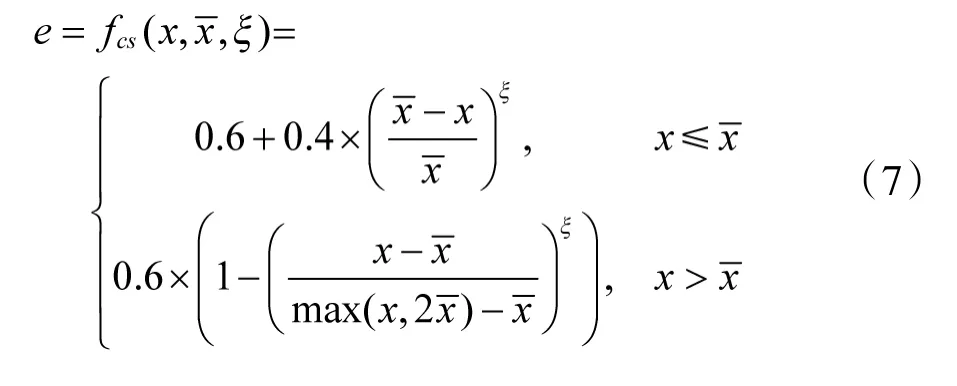
效益型功效函数与成本型功效函数均是在非线性可导S型函数的基础上构造的，符合机载雷达性能指标的饱和特性。一方面，机载雷达的某项性能指标有其物理或当今技术实现能力的极限；另一方面，改变机载雷达某项性能所带来的效能变化本质上也有S型曲线的趋势。

图2　性能指标的功效函数

2.4指标效能计算

机载雷达的作战能力是指机载雷达发现与监视目标的能力，其效能计算式如下:

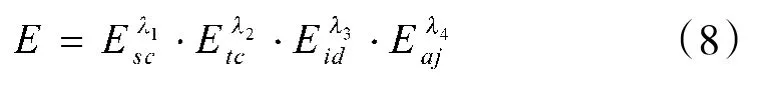
式中:Esc、Etc、Eid、Eaj分别表示机载雷达搜索能力、跟踪能力、识别能力、抗干扰能力的效能值；i表示权重系数，。

搜索能力是指机载雷达发现目标的能力，其效能计算式如下:

式中:R、［αmin，αmax］、［βmin，βmax］、T、δs、δv、δα、δβ、ΔθA、ΔθE、ΔR分别表示机载雷达的最大探测距离、方位覆盖范围、俯仰覆盖范围、搜索周期、距离误差、速度误差、方位角误差、俯仰角误差、方位角分辨率、俯仰角分辨率、距离分辨率；为作战任务规定的性能值；ξi为临界弹性系数；fb（fx，x，ξ）、fc（sx，ξ）分别表示效益型功效函数、成本型功效函数；i表示权重系数，， 0≤i≤1，i=1，2，…，7。

跟踪能力是指机载雷达对目标进行连续监视的能力，其效能计算式如下:

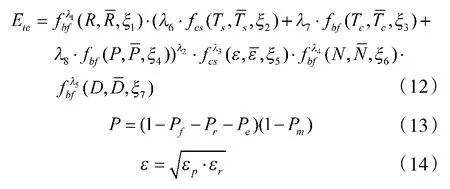
式中:R、Ts、Tc、Pf、Pr、Pe、Pm、εp、εr、N、D分别表示机载雷达的最大跟踪距离、航迹起始平均时间、航迹维持平均时间、虚假航迹率、冗余航迹率、误跟踪率、遗漏航迹率、目标位置误差、目标速度误差、最大跟踪目标数、数据更新率；为作战任务规定的性能值；ξi为临界弹性系数；fbf（x，x，ξ）、分别表示效益型功效函数、成本型功效函数；i表示权重系数， 0≤i≤1，i=1，2，…，8。

识别能力是指利用机载雷达获得的目标特征信息，并结合先验知识对目标身份进行判断的能力，其效能计算式如下:

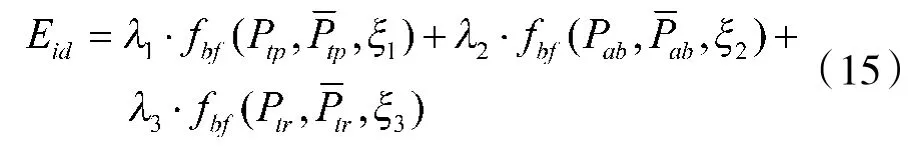
式中:Ptp、Pab、Ptr分别表示机载雷达对目标的类型识别率、属性识别率、威胁识别率；为作战任务规定的性能值；fbf（x，x，ξ）表示效益型功效函数；ξi为临界弹性系数；表示权重系数i≤1，i=1，2，3。

抗干扰能力是指机载雷达在干扰环境中工作时，消除或抑制干扰的能力，其效能计算式如下:

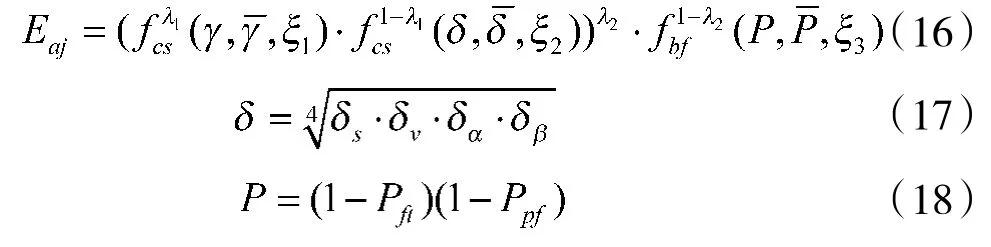
式中:γ、δs、δv、δα、δβ、Pft、Ppf分别表示探测范围压缩度、距离精度降幅、速度精度降幅、方位角精度降幅、俯仰角精度降幅、示假干扰成功率、拖引干扰成功率；为作战任务规定的性能值；ξi为临界弹性系数；fbf（x，x，ξ）、fcs（x，x，ξ）分别表示效益型功效函数、成本型功效函数；表示权重系数，，i=1，2。

3　实例分析

以甲型机载雷达和甲改型机载雷达为例，运用本文所提模型来评估二者的作战效能。限于篇幅，这里仅列出雷达搜索能力的评估情况。两款雷达的搜索性能指标如表2所示。

结合表2中的数据，利用式（5）～式（7）与式（9）～式（11）计算出两款雷达的搜索效能值，分别为Esc（甲）=0.67，Esc（改）=0.85。Esc（改）＞Esc（甲）表明甲改型雷达的搜索效能优于甲型雷达的搜索效能。从表2中可以看出，与甲型雷达相比，甲改型雷达在探测距离、方位覆盖范围、俯仰覆盖范围、定距精度、距离分辨率等重要指标上有显著提升。因此，甲改型雷达的搜索能力强于甲型雷达的搜索能力。在空中对抗演练中，两架同型号战机分别装备甲型雷达、甲改型雷达，最终装备甲改型雷达的战机胜9负1，这与两款雷达作战效能的评估结果相符。

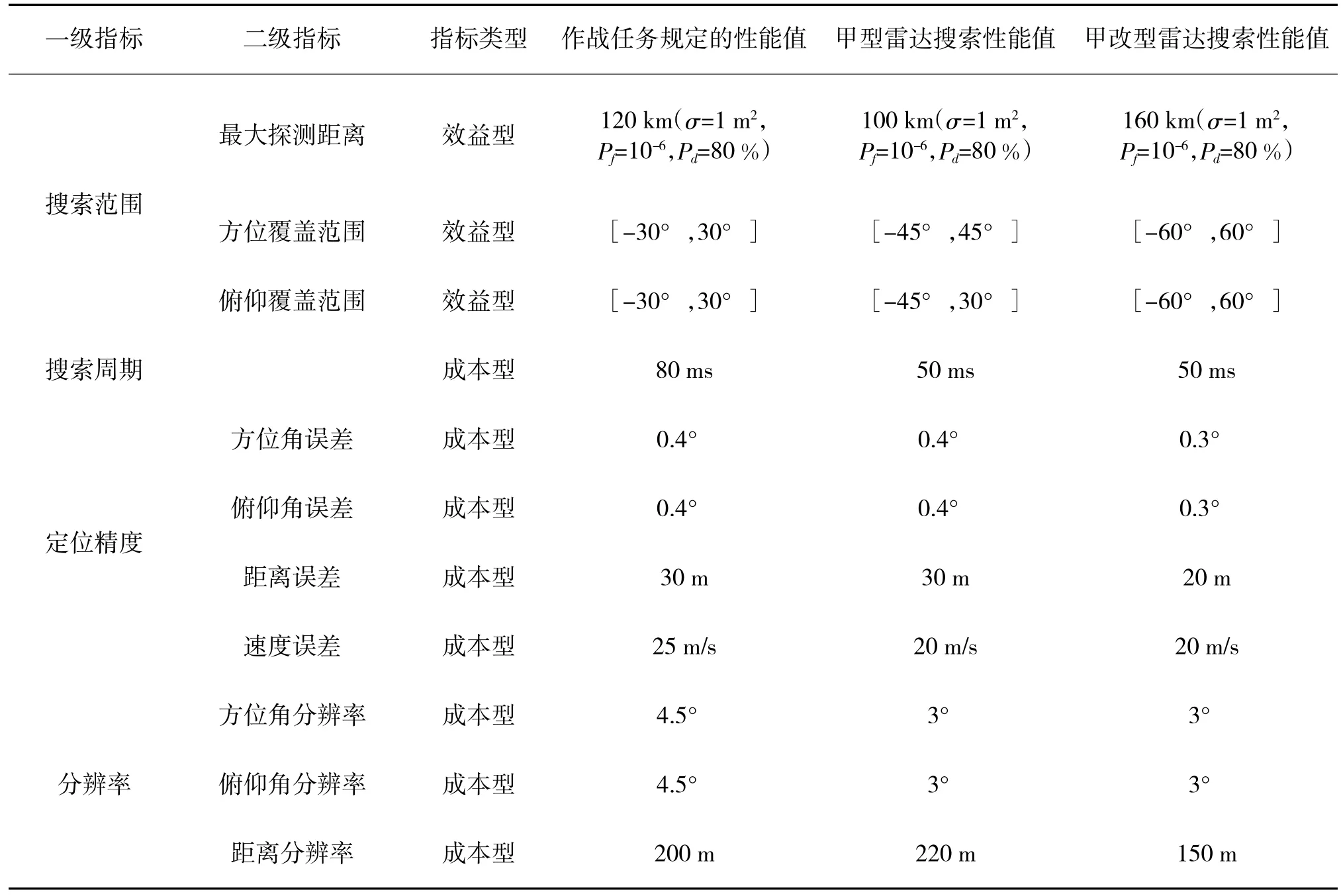
表2　机载雷达的搜索性能指标

4　结论

由于空战环境的复杂性以及敌方武器装备战技术特征的未知性，在对机载雷达的作战效能进行评估时，评估专家往往无法给出完整的指标权重信息。因此，本文结合在残缺判断矩阵上的研究成果，提出了权重信息不完全的机载雷达作战效能评估模型。该模型考虑了不同专家所给残缺判断矩阵的质量差异，削弱甚至劣质的残缺判断矩阵对评估结果的影响，使得评估结果更趋于客观合理。

［1］王云辉，高晓光，郑俊.基于攻击区匹配的机载雷达作战效能评估方法［J］.火力与指挥控制，2010，35（8）:32-36.

［2］陈辉，雷霆，闫达亮.天波超视距雷达作战效能综合评估研究［J］.雷达科学与技术，2014，12（2）:127-132.

［3］李教，敬忠良，王安，等.机载雷达的基本效能模型［J］.火力与指挥控制，2003，28（3）:12-14.

［4］陈世国，沈齐.基于灰色理论的机载预警雷达效能评估技术［J］.现代雷达，2008，30（7）:28-32.

［5］焦广伦，陆军.机载脉冲多普勒雷达探测性能的评估［J］.电讯技术，2009，49（11）:80-84.

［6］唐政，高晓光，张莹.机载雷达探测系统效能评估模型分析［J］.火力与指挥控制，2007，32（11）:21-23.

［7］叶义成，柯丽华，黄德育.系统综合评价技术及其应用［M］.北京:冶金工业出版社，2006.

Evaluation Model of Airborne Radar Operational Effectiveness with Incomplete Weight Information

ZHANG Zhong
（Southwest China Institute of Electronic Technology，CETC Key Laboratory of Avionic Information System Technology，Chengdu 610036，China）

For the problem of airborne radar operational effectiveness evaluation，in which index weight information is incomplete，an evaluation model is proposed.For incomplete judgment matrix given by expert，its consistency criteria is established.Combined with the best consistency ratio of incomplete judgment matrix，a single objective optimization model is constructed to calculate index weight.Based on this，an evaluation model of airborne radar operational effectiveness with incomplete weight information is proposed.Finally an example is given to validate the effectiveness of the proposed model.

airborneradar，operationaleffectiveness，evaluationmodel，incompletejudgmentmatrix

TN958

A

1002-0640（2016）06-0161-05

2015-05-06

2015-06-27

张忠（1986-），男，河南周口人，博士，工程师。研究方向：航空综合传感器系统效能评估。