基于统计加权的单传感器数据融合算法

李军，黄力伟

（海军大连舰艇学院，辽宁大连116018）

基于统计加权的单传感器数据融合算法

李军，黄力伟

（海军大连舰艇学院，辽宁大连116018）

单传感器数据融合是十分重要的实际问题。为了提高数据处理的敏感性和精度，在研究基于关系矩阵的数据融合方法的基础上，提出了基于统计加权的数据融合方法，并对两种方法进行了对比分析。实例仿真表明，基于统计加权的数据融合方法优于基于关系矩阵的数据融合方法，该方法能减小无效测量值的范围，并且对测量值的变化更敏感。

数据融合，关系矩阵，统计加权

0　引言

在实际应用中，当单传感器对某特性参数进行测量时，在较短的时间内，会得到多个测量值。如何对单传感器的多个测量值进行数据融合以得到最佳的融合数据，这一问题具有十分重要的现实意义［1］。在研究基于关系矩阵的数据融合方法的基础上，本文提出一种基于统计加权的数据融合方法，并对两种方法进行了对比分析。

1　基于关系矩阵的数据融合算法

基于关系矩阵的数据融合方法根据传感器的测量值，确定测量值间的置信距离矩阵，然后利用阈值得出测量值间的关系矩阵，根据关系矩阵得出测量值的综合支持程度［2］，从而确定融合集，最后根据极大似然法确定融合集的最佳融合数据。

用单传感器测量某特性参数时，设测量值X服从Gauss分布，即，xi、xj分别表示第i、j次的测量值，为了衡量xi、xj之间偏差的大小，引入置信距离测度，dij的值称为传感器的测量值xi、xj的置信距离测度，dij可以直接借助误差函数求得［3-4］：

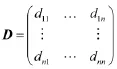
选定阈值ε，当置信距离测度dij＜ε时，认为两个测量值相互支持，值为1（rij=1），否则为0（rij=0），得到关系矩阵为：

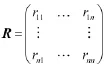
其中rij表示测量值xj对测量值xi的支持程度。

如果传感器的某个测量值被其他测量值所支持，则此测量值是有效的。若传感器的测量值不被其他测量值所支持，或只被少数其他测量值所支持，则此测量值是无效的，应把这样的值删掉。所有有效测量值的集合称为融合集。

设单传感器测量值经关系矩阵处理后，所得融合集为（x1，…，xm）。下面用极大似然法［5］求最佳融合数据。

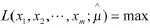
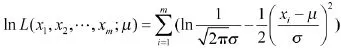
解得

2　基于统计加权的数据融合算法

基于关系矩阵的数据融合方法中，阈值的选定带有很大的主观因素，并且不能反映测量值的差异性。下面给出一种基于统计加权的数据融合方法，此方法在利用传感器测量值统计规律的基础上，有效、客观地反应了测量值间的差异性对融合结果的影响。

2.1算法的基本思想

基于统计加权的数据融合方法根据传感器的测量值，依据“3σ法则”［5］，去除无效测量值。然后利用选定的步长划分有效区间，根据测量值在有效区间的位置，确定置信概率向量。对置信概率向量归一化可得测量值的加权向量。最后根据测量值与加权向量的乘积可得最佳融合数据。

设传感器第i次测量值为xi。以步长L划分，如果，则定义xi的置信概率为：

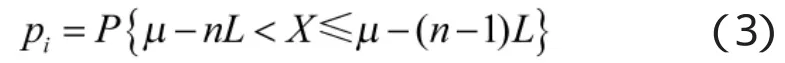
根据置信概率，可定义置信概率向量：

当L=σ时，区间划分和置信概率如下：

定义加权向量：

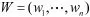
其中

加权向量W是置信概率向量P归一化后的结果。特别地，传感器的无效测量值在加权向量W中的权值为0。

最佳融合数据k为：

2.2算法步骤

第2步：确定步长L，并结合σ的值，求得各测量值的置信概率，从而确定置信概率向量P，对P进行归一化处理，可得加权向量W。

第3步：计算k=X*WT的值，如果k==μˆ，则传感器的最佳融合数据为k；如果k≠μˆ，令μˆ=k，重复第2步和第3步。

经过l次迭代后，最终的加权矩阵为W（l），传感器的最佳融合数据输出k（l）为：

3　算法举例

假设单传感器对某特性参数测量值如下：

其中传感器的均方差σ=0.1。

3.1基于关系矩阵的数据融合算法

由（1）式可得测量值的置信距离矩阵为：

表1　测量值

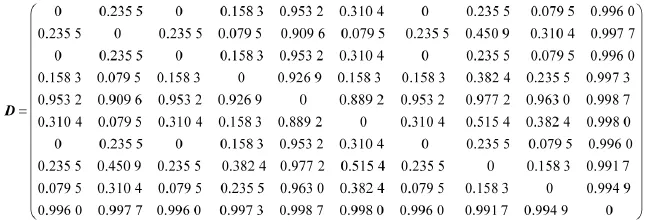
当ε=0.6时，得到关系矩阵为：

假定被另外至少6个测量值支持的数据为有效数据，则融合集为。

运用文献［3］的方法，根据式（2）可得到最优融合数据为0.8938。

3.2基于统计加权的数据融合算法

取步长L=σ，经3次迭代后，由式（3）可得置信概率向量为：

由式（4）可得加权向量为：

由于x10的加权系数为0，所以融合集为。

表2　仿真迭代结果

如表2所示，3次迭代后最佳融合数据为0.884 6。

4　算法比较

为了对两种算法进行性能对比，采用控制单一变量的方法，令观测值x5为自变量，变化范围为［0.5，1.28］。传感器均方差σ=0.1，测量值如表3所示。

在进行MATLAB仿真时，x5以步长0.02变化。如图1所示，其中算法1是基于关系矩阵的数据融合算法，算法2是基于统计加权的数据融合算法。

图1　算法仿真

表3　测量值

在对算法1进行试验仿真时，取阈值ε=0.6，并设定至少被6个测量值支持的数据为有效数据。从图1可以得到：当时，算法1的最优融合数据为0.893 8；当时，最优融合数据和x5成线性关系，即最优融合数为。产生此现象的主要原因是：当时，测量值x5和x10都被算法1认为是无效的数据，所以最优融合数据根据式（2）是的平均值，为0.893 8；当时，测量值x10被算法1认为是无效数据，所以最优融合数据和x5成线性关系，为。

在对算法2进行试验仿真时，取步长L=σ。从图1可以得到：当时，算法2的最优融合数据为0.893 8；当时，最优融合数据和x5成分段线性关系。产生此现象的主要原因是：当时，测量值x5和x10都被算法2认为是无效的数据，所以加权系数向量W的值和算法1的各加权值相同为1/8，最优融合数据根据式（6）是的平均值，为0.893 8；当时，测量值x10被算法2认为是无效数据，而x5被认为是有效数据，但是由于它与最佳融合数据偏离程度不同，会被划分到不同的区间，赋予相应的权值，尤其是当时，x5被赋予和其他有效数据一样的加权值，所以在区间［0.8，0.92］，算法2和算法1的结果相同。随着缩小步长L的取值，算法2的仿真图像将变得越来越平滑。

从以上分析中可以得到：两种算法在融合数据时都能把错误测量值x10排除，较好地删除了无效数据。但是，算法1较算法2扩大了无效测量值的范围。而且由于算法1利用极大似然法求最佳融合数据，所以它对有效测量值赋予的权值相同为1/m（其中m为融合集中有效值得个数），只是简单地取融合集的平均数。而算法2根据测量值偏离最佳融合数据程度的不同，赋予测量值不同的权值，因此，算法2对测量值的改变更敏感，也更好地反映了测量值的差异性。但是算法2要结合具体的实际问题划分置信概率区间，并且随着细化置信概率区间，融合结果的收敛速度会变慢。

5　结论

在融合单传感器多次测量值时，基于关系矩阵的数据融合算法中阈值和测量值支持数据个数的选定过于经验化，不能很好地对实际情况作出判断，融合结果受主观影响较大［6］。而基于统计加权的数据融合算法在利用“3σ”法则的基础上，依据测量值偏离融合值的程度确定加权值，能客观地对测量值进行融合，可以在多次迭代后得到最佳融合数据。

［1］蔡菲娜，刘勤贤，朱根兴，等.数据融合方法在单传感器系统中的应用［J］.数据采集与处理，2005，20（3）：88-90.

［2］王丽，杨全胜.多传感器数据融合的一种方法［J］.计算机技术与发展，2008，18（2）：80-82.

［3］陈福增.多传感器数据融合的数学方法［J］.数学的实践与认识，1995，25（2）：11-15.

［4］曾黎，蒋沅.多传感器数据融合的数学方法研究［J］.云南民族大学学报，2010，19（9）：321-324.

［5］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2013.

［6］刘建书，李人厚，常宏.基于相关性函数和最小二乘的多传感器数据融合［J］.控制与决策，2006，21（6）：714-716.

Single Sensor Data Fusion Method Based on Statistical Weighting

LI Jun，HUANG Li-wei
（Dalian Naval Academy，Dalian 116018，China）

It is important to the question of a single sensor data fusion.For improvingsensitivity and accuracy of data fusion，this paper which has studied the data fusion method based on relational matrix presents a data fusion method based on statistical weighting and compares between two methods. The simulation results show that the data fusion method based on statistical weighting is better than which based on relational matrix.The method can reduce the range of invalid measured values，and is more sensitive to the measured value changes.

datafusion，relational matrix，statistical weighting

TP274

A

1002-0640（2016）10-0184-04

2015-08-16

2015-09-16

李军（1988-），男，河南驻马店人，硕士。研究方向：目标识别，数据融合。