装备保障人员优化配置方法研究

张继尧，高铁路，陈为元，陈义军，李志伟

（1.空军勤务学院，江苏徐州221000；2.军械工程学院，石家庄050003）

装备保障人员优化配置方法研究

张继尧1，高铁路2，陈为元2，陈义军1，李志伟2

（1.空军勤务学院，江苏徐州221000；2.军械工程学院，石家庄050003）

将装备保障人员按级别分为操作人员、维修人员及管理人员，结合人员进入、培训和退出的状态，构造了状态转移矩阵，求出了各级别人员数量。定义了不同级别针对不同任务的保障效率，按照保障人员完成最高效率任务构建了最优化配置模型。通过实例验证了模型的实用性。

保障人员，状态转移，优化配置，模型

0　引言

保障人员作为装备保障的主体，是保障过程的执行者，直接影响着装备保障效能的发挥。对保障人员进行合理配置，可以使保障任务能及时、高效地完成，使装备保障获得最大的效益［1］。当前，保障人员优化配置模型和方法主要有指派模型［2］、目标规划模型［3］、实体关系模型［4］以及借用经济学中的边际理论［5］、无差异曲线［6］等方法。但是人员配置实际中往往存在人员动态变化的情况，例如荆海英、杨兆宇基于控制理论建立了人员动态模型［7］。本文结合装备保障人员级别层次特点，考虑人员动态转移，运用线性规划模型，对保障人员按任务进行分配，力求使得保障任务综合保障效率最高，从而实现保障人员的优化配置。

1　保障人员动态描述

装备保障人员主要分为装备操作人员、装备维修人员和装备管理人员3个类别，由装备操作人员或装备维修人员通过培训获得一定资格后可以转移为下一类别，根据任务需要可以直接进行各类别人员之间的调整，如图1所示。

图1　人员状态转移示意图

如果假设保障人员在某一时刻t所处的各类状态组成一个系统S（向量），则系统中保障人员状态分为以下两种：一是培训态li（i=1，2，3分别表示保障人员处于培训状态）；二是正常态ki（i=1，2，3分别表示保障人员处于3个类别的状态）。其中，培训态l3为人员达到装备管理人员后的培训，在实际中没有意义，因此，可以舍去。于是，在某一时刻t系统可表示为一个状态空间集合，即。

定义系统S为保障人员系统，假设人员在该系统中的动态转移具有随机和无后效性，即服从非齐次马尔科夫过程，则在时刻t时人员的随机转移概率服从概率矩阵PS（t）

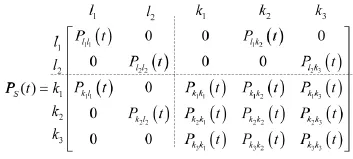
其中，Pij（t）表示从状态i向状态j转移的人员占原处于状态i人员的比例，即状态i转移为状态j的概率。

分析矩阵PS（t）可知，其状态转移过程可描述为4种情况：

①某一类别人员符合培训条件进入培训状态（矩阵PS（t）左下）；

②培训完考核不通过继续停留在培训状态（矩阵PS（t）左上）；

③培训完成，即进入下一类正常状态（矩阵PS（t）右上）；

④正常态之间直接进行相互调整（矩阵PS（t）右下）。

2　保障人员动态模型

2.1保障人员进出分析

2.1.1保障人员退出系统的状态

在系统内部动态转移之外，还需要考虑人员进入和退出系统的情况。首先定义时刻t处于系统S内各个状态的保障人员数量，可用向量表示为

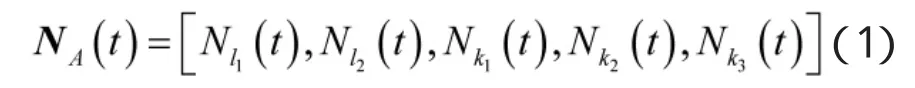
假设系统S外存在一个状态k4，表示保障人员退出系统的状态，那么可以得出人员的退出概率为

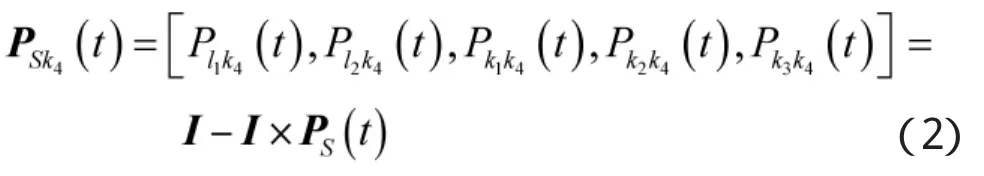
式中，I=［1，1，1，1，1］。

所以，在时刻t由于人员退出造成的人员空缺为

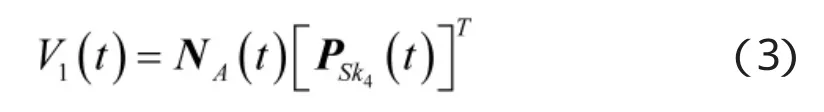
2.1.2保障人员进入系统的状态

保障人员出现空缺后需要进行适当的补充，即需要有一定的人员进入系统S。人员进入系统的状态分为两类情况：一类是具有一定保障能力的人员直接进入系统，另一类是新分配的保障人员经过岗前培训进入系统。

①具有一定保障能力的保障人员进入。

具有保障能力的人员进入系统可按照其素质不同，直接分配至3个类别的保障人员。假设系统S外存在一个进入系统前的状态，定义该状态为k0。那么保障人员直接进入系统的概率可表示为

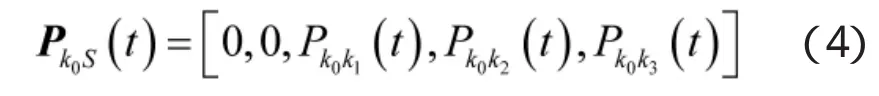
②经过岗前培训的保障人员进入。

新分配的保障人员需要通过一个预备培训才可以上岗，因此，系统S外还应存在一个进入系统的预备培训状态，定义该状态为l0。那么经过预备培训进入系统的概率为

式（5）中，I=［1，1，1，1，1］。

显然，在时刻t处于状态l0的人员，在时刻t+1加入系统且处于状态ki（i=1,2，3）的概率为，写成向量形式为

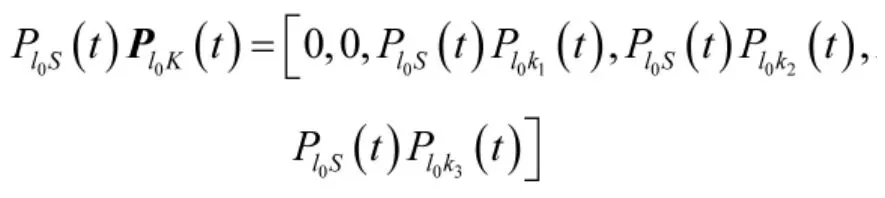
2.2保障人员动态模型

结合上述分析可知，在时刻t，处于系统S内部各个状态的保障人员数量以向量表示为

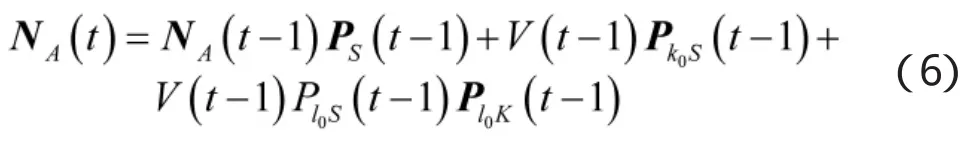
将式（3）代入式（6）有

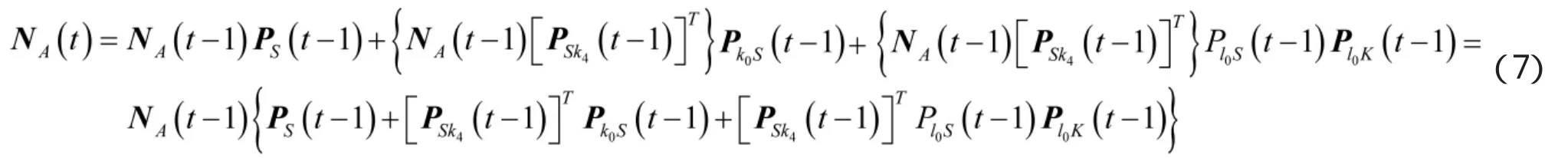
式（7）可简写为

式（8），P1（t-1）第1项表示系统S内部的培训或直接调整；第2项表示为弥补人员退出的空缺，人员直接调入系统的调整情况；第3项表示为弥补人员退出的空缺，人员经过岗前培训补充至系统的调整情况。可见，式（8）总结了保障人员包括进入、培训、提升及退出的动态规律，可以成为机关调整装备操作人员、装备维修人员和装备管理人员的依据。

3　保障人员动态优化配置模型

考虑到实际中3个级别的保障人员存在差异性，即不同级别人员在完成同类任务时体现的能力并不一致，这对人员配置有很大的影响，借鉴能力成熟度模型集成（Capability Maturity Model Integration，CMMI）的方法［9］，本文将此影响定量表示为保障效率：

其中：ηij为在某一时刻t，第i级别保障人员完成第j类任务的保障效率（每人单位时间完成任务量）。βij为第i级别保障人员完成第j类保障任务的能力系数；θij为第i级别保障人员与第j类保障任务的匹配度。

由于保障人员的能力系数和匹配度都是较为主观的评价值，可尽量结合实际制定评价标准，采用专家评估、AHP等方法进行评定。表1和表2分别给出了能力系数和匹配度的评价标准。

需要说明的是，按照评价标准得出的分数为百分制，还需要进行标准化转化为属于［0，1］内的值，标准化公式为：

其中，wk为标准化后的值；Zk为某级别保障人员中第k个评价分数为某级别保障人员评价分的平均值；S为标准差。

能力系数评价根据职务说明书确定保障人员各因素的评定等级及标度分值，如1表所示。

匹配度评价主要按照人员各项素质［10］与保障任务的符合程度，分为6个标度等级：完全符合、基本符合、符合、有时符合、不符合、无，依次对应的标度如表2所示。

假设：

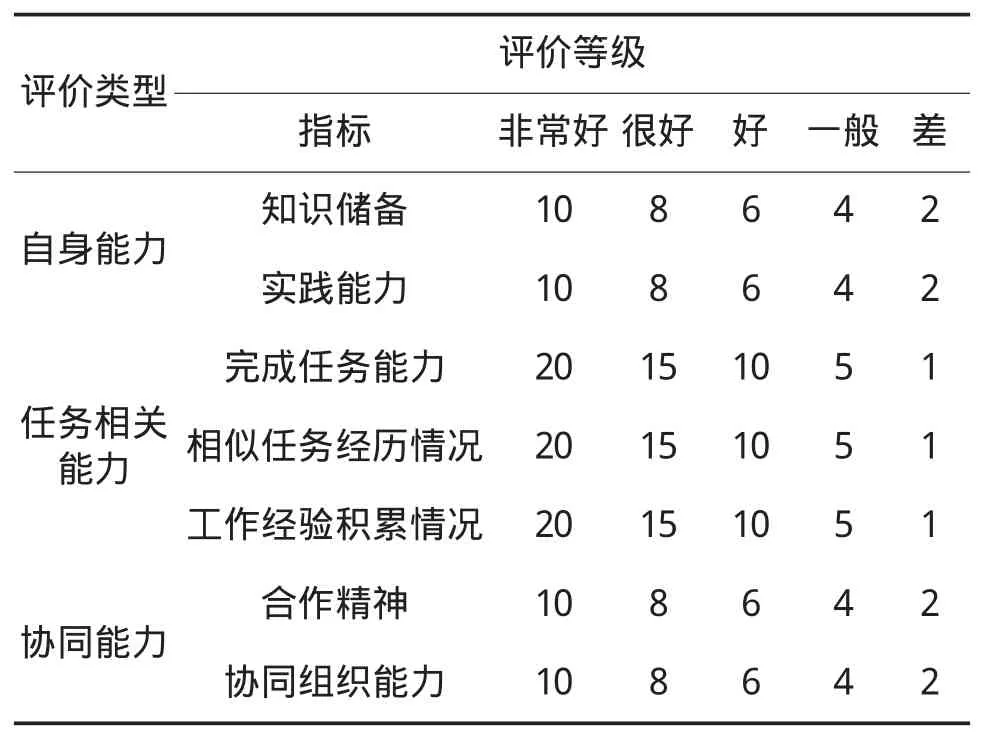
表1　保障人员能力系数评价标准

表2　保障人员匹配度评价标准

①处于培训态的人员无法完成保障任务；

②同一类别的所有保障人员在完成同一保障任务时拥有相同的保障效率；

③在完成某种保障任务时，各类别的保障人员完成的任务量与其保障效率成正比；

④第j类保障任务的保障人员需求量为nj。

如果当前有n个保障任务，在t时刻分配至第j个保障任务的第ki类别保障人员数量为；则有下述建模条件

在考虑人员最优配置时，可以直接考虑使保障人员去完成保障效率最高的任务，优化模型表示为

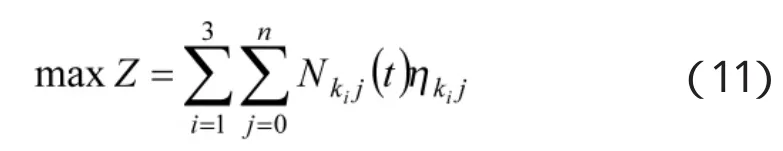
该模型为人员总量约束的线性规划模型，求解过程中为了最优解可以解出，可以结合式（8）调整约束条件中保障人员数量的值。

4　示例分析

某单位2014年保障人员状态如表3所示。表4列出了2015年计划保障任务的保障人力需求值，2015年无专业或设备增加的计划。如果该单位装备操作人员、装备维修人员每年以8%、6%的概率进行培训，培训后当年不进行类别转换；3个类别保障人员各有90%的人员不作类别调整，且装备操作人员和装备维修人员各有5%、2%的概率调入下一类，并且无跨类（k1→k3）和降类（k2→k1，k3→k1，k3→k2）的调整。人员进入必须经过岗前培训，且通过岗前培训平均进入系统的保障人员分配比率为75%、20%和5%。2014年底，装备操作人员、装备维修人员和装备管理人员的退出概率分别为5%、3%、和2%，处于培训状态的人员不退出系统。试通过保障人员动态控制的方法，求解2015年度保障人员的最佳配置方案。

表3　某单位2014年度保障人员实力统计

表42015　年度保障任务人力需求

解：下面从动态调整和人员配置两个步骤解决该问题。

①动态调整。

将上述数据代入式（8）有

可知，在给出培训率、类别调整概率以及人员退出率的情况下，2015年度经过动态调整后的装备操作人员、装备维修人员和装备管理人员的人数分别为90.9、68.95和10.42，较2014年的人数（101、71和10）有所变动，基本符合实际情况。比较式（8）可知，人员进入系统的概率是当前未给出的变量，如果各类人员变动后，出现无法满足任务需求的情况，单位可以通过控制变量来进行人员配置。

②人员配置。

根据表1和表2的标准对保障人员能力和任务匹配度进行打分，进行标准化后分别按行和列填入表5，并相乘得出保障效率数据。例如，装备维修人员完成值勤任务的能力系数评价值标准化后为0.844，完成值勤任务的匹配度评价值标准化后为0.790，则填入表5第2行第1列的值为0.844×0.790=0.667。

表5　保障人员完成各项任务的保障效率表

由于处于培训状态的人员不参与保障任务，所以只考虑3个类别的保障人员数量，则依据式（11），保障人员配置模型可表示为

约束条件为

其中，由于人数均向上取整，所以需要补充人数比理论计算值要多。即在2015年度，当装备操作人员补充39+27+31-91=6（人）、装备维修人员补充18+13+11+14+17-69=4（人）时，可以按最高效率完成所要求的任务。

表6　保障人员配置方案

需要说明的是，本例只对人员通过培训进入系统的比例进行了动态的调整与配置。人员调整与配置的方法还包括控制人员退出概率、调节系统内部人员转移比率等，调整方法与本例类似，本文不再进行讨论。

5　结论

本文将保障人员按级别分为操作人员、维修人员及管理人员，结合人员进入、培训、退出的状态，分析其状态转移方法，并构造了状态转移概率矩阵，构建了保障人员的动态模型。通过定义不同级别保障人员针对不同任务的保障效率，按照保障人员完成最高效率的任务，构建了最优化配置模型。下一步需要在系统内部人员流动概率方面继续研究，在此基础上实现最优化配置。

［1］刘建国，毕进南.通信装备保障概论［M］.北京：军事科学出版社.2006.

［2］朱益军，项阳.用指派问题求解企业人力资源配置的最优方案［J］.天津商学院学报，2003，23（3）：32.

［3］林晶晶.企业多项目管理中的人力资源配置研究［D］.成都：西南交通大学，2006.

［4］侯莉莉，姚玉南，范世东，等.基于船舶大修的人力资源优化配置研究［J］.武汉理工大学学报（交通科学与工程版），2011，35（2）：325-328.

［5］谭元发.边际理论在企业人力资源配置中的应用［J］.技术经济与管理研究，2003，24（1）：76-77.

［6］王恺，高崎，王登山，等.无差异曲线在部队修理机构人员配置中的运用［J］.兵工自动化，2007，26（8）：20-21.

［7］荆海英，杨兆宇.人力资源规划的动态预测方案［J］.预测，2001，20（2）：23-25.

［8］王俊.人力资源柔性管理与人员流动优化模型研究［D］.天津：天津大学，2005.

［9］CMMI Product Team.Capability maturity model integration（CMMISM，Version 1.1）［R］.CMMISM for Systems Engineering，Software Engineering，and Integrated Product and ProcessDevelopment（CMMI-SE/SW/IPPD，V1.1）Staged Representation，2001.

［10］朱平利.企业中人岗匹配度测算模型及其应用［J］.湖北工业大学学报，2009，24（6）：58-60.

Study on Optimization Allocation Methods of Equipment Support Personnel

ZHANG Ji-yao1，GAOTie-lu2，CHENWei-yuan2，CHENYi-jun1，LI Zhi-wei2
（1.Air Force Logistics College，Xuzhou 221000，China；2.Ordnance Engineering College，Shijiazhuang 050003，China）

The support personnel are divided into three categories：operator，maintenance personnel and administrator.A state transition matrix is established combining with the training station，then the numbers of personnel can be solved.Support efficiency of personnel to task is defined，and optimization allocation model of support personnel is developed.An instance is get to analyze and prove the practicability of the model，finally.

supportpersonnel，statetransition，optimizationallocation，model

E92

A

1002-0640（2016）10-0192-05

2015-07-05

2015-08-07

张继尧（1992-），男，天津人，硕士。研究方向：装备保障理论与应用、航空弹药勤务。