玻璃纤维土的力学性能研究

2016-11-15张瑞斌

山西交通科技 2016年5期

张瑞斌

（山西省交通科学研究院，山西太原 030006）

玻璃纤维土是指利用特定的机械设备将玻璃纤维均匀加入土体中，利用玻璃纤维与土体之间的摩擦力制止土体的移位，从而实现土体的加固[1]。相比于一般加筋土，如编织袋、土工格栅等，玻璃纤维不仅能控制土体的水平变形，还可以有效地控制侧向和竖向变形[2]。这是因为拌合后的玻璃纤维土，其纤维均匀地分布于土体中，土体利用玻璃纤维较好的抗拉性能，将自己牢牢黏聚在一起，具有各向同性的力学性质。同时，与其他纤维相比，玻璃纤维具有耐腐蚀、吸水性少、强度高、延伸率低、加工性好等特点。

国内外学者纤维土已展开了较全面的研究。Sivakumar等[3]通过研究发现，纤维的掺入能够快速地提高土体的抗剪强度；Garry等[4]分析了土体应力和应变与纤维角度的关系；张旭东等[5]通过研究发现，随着纤维的加入，土的黏聚力、韧性和塑性均明显改善。但目前，对玻璃纤维土的工程力学特性研究尚不全面。

本文通过室内三轴试验对其强度及变形特性进行研究。分析了玻璃纤维掺入比、纤维长度对玻璃纤维土抗剪强度的影响；通过动三轴实验分析了玻璃纤维土的动强度及动模量。

1 玻璃纤维土的作用机理

可用“弯曲机理”与“交织机理”来分析玻璃纤维补强土体的作用机理。弯曲机理是将掺入土体中的玻璃纤维分布形态看作连续分布的无数均匀没有直线段的弯曲形态。当外力作用土体时，土体中玻璃纤维受拉，由于玻璃纤维为弯曲形态，其凹侧对土颗粒作用压力与摩擦力，从而对土体进行加固作用。交织机理是指大量玻璃纤维无序地分布在土体中，纤维之间存在无数的交织点，将整个纤维连接成一个统一的网格，当某一交织点受力时，会牵扯整个网格，就会形成一个统一的空间受力体。

2 玻璃纤维土的三轴试验研究

2.1 试验设备

a）静三轴试验试验所采用的三轴仪为SJ-1A型应变控制式，产自南京。仪器由试验机器、压力控制室以及测量系统3个部分组成，利用TSW-3进行数据采集。

b）动三轴试验试验采用电磁式GDS动三轴仪，产自英国GDS公司。仪器由静力系统、激振系统及量测系统组成，该仪器能够测量小应变并自动进行数据采集。

2.2 试验材料

本文试验所采用的土样为ISO标准砂，其级配良好，物理参数如表1所示。试验所采用的玻璃纤维为无碱玻璃纤维丝，其物理参数如表2所示。

表1 砂土的物理参数指标

表2 玻璃纤维的物理参数

2.3 试验方法

a）静三轴试验试件为高200 mm、直径100 mm的圆柱体，采用三轴不固结不排水试验，以玻璃纤维掺入比例、纤维长度作为两个水平因素。如表3所示，玻璃纤维掺入比分别取1%、2%、3%、4%，玻璃纤维的长度分别为5 cm、10 cm、15 cm、20 cm，为使试验得到的强度包络线完整，取4个围压值，分别为50 kPa、100 kPa、150 kPa、200 kPa。

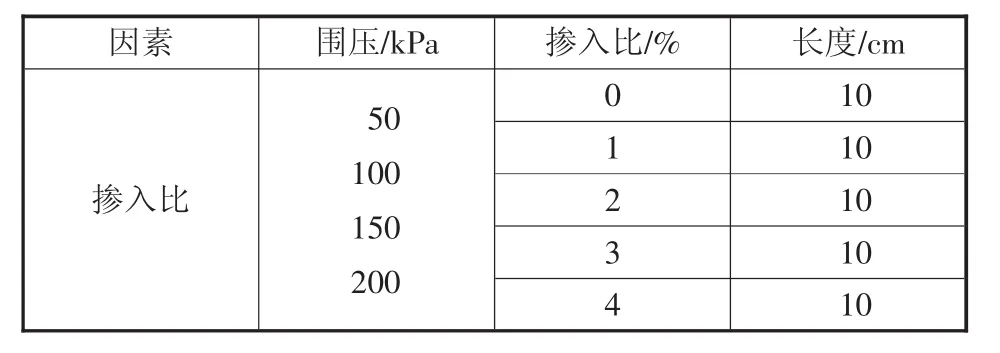
表3 玻璃纤维土的试验工况

b）动三轴试验分别制作玻璃纤维掺入量为0%、2%的试件，试件为直径70 mm、高140 mm的圆柱体。试验时，动应力加载的频率为0.5～5 Hz，压力分别为100 kPa、200 kPa、300 kPa。将水压加大至所需围压，施加动应力直到应变量达到5%，即认定试件达到破坏，试验结束。

3 玻璃纤维土的试验结果分析

3.1 玻璃纤维土的应力-应变曲线

通过对不同玻璃纤维掺入量、玻璃纤维长度以及不同围压条件下的玻璃纤维土三轴不固结不排水试验，可得如图1～图3所示结果。

图1 不同玻璃纤维掺入量下的应力-应变曲线

由图1可知，随着玻璃纤维长度与掺入量的增加，玻璃纤维土的可承受压力值增加，强度逐渐增加。轴向应变小于1.8%左右时，玻璃纤维土试块为弹性变形，当轴向应变大于3%后，玻璃纤维土试块的应力-应变曲线趋于平缓。由图1可以明显看出，与无筋砂土相比，在相同轴向应变的情况下，玻璃纤维的掺入明显限制了土体的变形，增加了土体的强度。同时，当玻璃纤维掺入量大于2%后，在受力初期，玻璃纤维土试块的应力-应变曲线斜率就开始增加，玻璃纤维的加固作用已体现。工程应用中，考虑到经济作用，可取玻璃纤维的掺入量为3%。

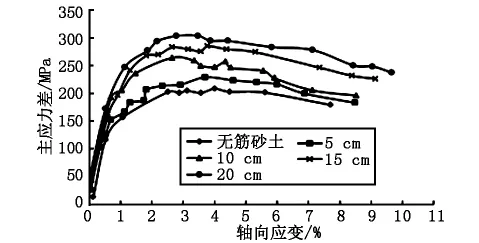
图2 不同玻璃纤维长度的应力-应变曲线

由图2可知，玻璃纤维土试块可承受压力值随着玻璃纤维长度的增加而逐渐增加，当玻璃纤维长度大于10 cm后，曲线的斜率增加，玻璃纤维的加固作用明显。在工程应用中，为使玻璃纤维拌合均匀，可取玻璃纤维长度为10 cm。

图3 不同围压下的应力-应变曲线

图3表明，玻璃纤维土试块的强度随着围压的增大而逐渐增大。另一方面，其曲线斜率也随之增加。

3.2 玻璃纤维土的抗剪强度指标

以黏聚力、内摩擦角作为玻璃纤维的抗剪强度指标值，本试验所用砂土的黏聚力为0，内摩擦角为38°。由摩尔库伦应力圆方法，求得不同玻璃纤维掺入量与长度下的黏聚力与内摩擦角如表4所示。

表4 玻璃纤维土的抗剪强度相关指标

由表4可知，玻璃纤维的掺入对黏聚力的影响较大，但对内摩擦角的影响较小。

3.3 玻璃纤维土的抗剪强度分析

试验可得玻璃纤维土抗剪强度与玻璃纤维掺入量、玻璃纤维长度的关系如图4所示。

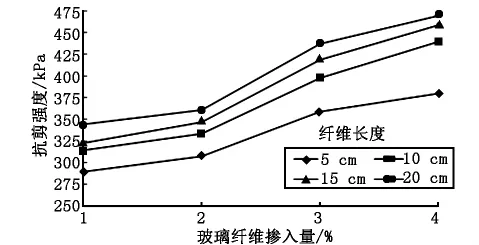
图4 玻璃纤维掺入比与纤维长度的抗剪强度关系(围压150 kPa)

图4为围压150 kPa时，玻璃纤维土试块在不同玻璃纤维掺入量与长度下的抗剪强度曲线。由图4可知，玻璃纤维的抗剪强度随着玻璃纤维含量和纤维长度的增加而增加，但不同含量的增加量则不同，玻璃纤维含量从2%增加到3%时，其抗剪强度的增长幅度最大，平均达到了18%左右。掺入量由1%增加到2%时，抗剪强度的增长幅度平均为9%左右；掺入量由3%增加到4%时，抗剪强度增长幅度平均为7%左右，这是因为随着玻璃纤维掺入量的增加，纤维与土颗粒的接触逐渐趋于饱和。

由图5可知，当玻璃纤维长度由5 cm增加到10 cm时，其抗剪强度的平均增长幅度最大，达到了10.1%左右。当玻璃纤维的长度大于10 cm后，抗剪强度的增长趋于平缓。

图5 玻璃纤维长度与围压的抗剪强度关系（玻璃纤维掺入量3%）

3.4 动强度的提取

由动三轴试验所得的试验数据可以直观看出动剪应力σd/2随破坏周数的对数lgNf的变化规律，其中动强度为10周破坏时对应的动剪应力。不同围压下，玻璃纤维掺入量分别为0%、2%的破坏周数与动剪强度关系曲线如图6、图7所示。

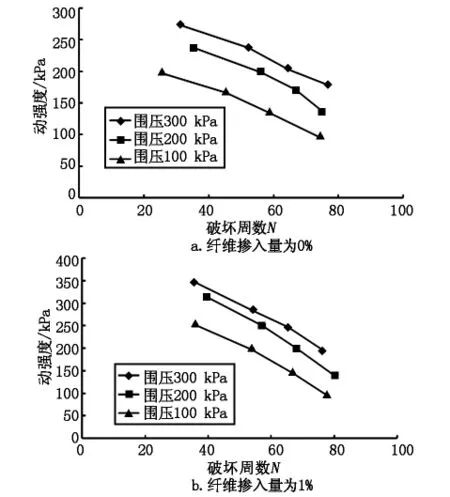
图6 玻璃纤维土的动强度曲线

由图6可得不同围压下，Nf=10时，玻璃纤维土的动强度结果如表5所示。

表5 玻璃纤维土加固前后的动强度 kPa

由表5可知，相比于纯砂土，掺入玻璃纤维后的砂土，其动强度平均增加了60 kPa，即提高了28.39%。另一方面，随着破坏周数的增多，玻璃纤维土的动强度减小，但其动强度随着围压的增加而增大。

3.5 动模量的提取

由动三轴试验所得试验数据，可得玻璃纤维土的应力-应变关系曲线如图7所示。

图7 动三轴试验下的应力-应变曲线

由图7所示应力-应变滞回曲线计算玻璃纤维土的弹性模量，如表6所示。

表6 玻璃纤维土加固前后的动模量 MPa

由表6可知，掺入2%玻璃纤维后的砂土，其动强度得到了有效的提高。这是因为玻璃纤维弯曲分布于砂土中，当玻璃纤维受拉时，摩擦力随即产生于弯曲处，由此便产生一种抗力。另一方面，玻璃纤维交叉处产生的力会随着整体受力的增加使玻璃纤维产生横向位移的趋势，而其他交织在一起的玻璃纤维便会阻止这种位移的产生，即形成一个受力新区，从而增加了玻璃纤维土的黏聚力，由τ=σtanφ+c可知，随着黏聚力c的增大，玻璃纤维土可承受的最大剪切应力增大，从而提高了动剪切强度τd，即提高了玻璃纤维土的抗液化强度。此外，由于玻璃纤维在砂土中随机分布，孔隙水压力的上升从而受到阻止，土的液化即变得十分困难，从而提高了土体抗液化强度。