变位系数对聚合物熔体齿轮泵挤出稳定性的影响

樊柯彬，毕超

变位系数对聚合物熔体齿轮泵挤出稳定性的影响

樊柯彬，毕超

（北京化工大学机电工程学院，北京 100029）

针对熔体齿轮泵齿轮啮合过程中齿槽容积变化，从而引起微观波动的问题，基于扫过面积法建立了外啮合变位齿轮泵流量计算模型。利用该模型，以齿轮泵平均流量和流量脉动率等参数为指标，分析了齿数增长时，高度变位、角度变位正传动和角度变位负传动等情况中齿轮变位系数对挤出稳定性的影响。

齿轮泵；挤出稳定性；变位系数

熔体齿轮泵在聚合物稳定挤出领域应用越来越广。由于齿轮泵的正位移输送特性，它可以有效地消除由喂料波动、塑化不均及供电波动造成的挤出宏观波动。但是由于齿轮泵的齿轮啮合过程中齿槽容积随齿轮啮合相位不断变化，所以齿轮实际工作中还会造成一定的微观波动，即齿轮泵流量脉动。流量脉动是衡量齿轮泵挤出稳定性的一个重要指标，很多学者在齿轮泵流量脉动方面开展了研究工作［1-3］。李秀明［4］介绍了选择变位系数的限制条件。司健［5］指出齿轮泵输送流体是靠齿轮转动时啮合点形成的吸、压腔室的容积变化来形成的，分析了齿轮泵参数对其输送性能的影响。邹曼等［6］研究了齿轮变位后齿轮泵的排量计算方法。齿轮变位修正后，齿轮的形状发生变化，排量计算公式推导时用到的齿轮厚度、齿顶高和齿根高也发生了相应的变化。杨国来等［7］研究了内啮合齿轮泵齿轮变位系数对流量脉动的影响。宗光涛等［8］对比了齿槽有效容积的排量计算方法和有效体积的排量计算方法，研究出了三维模型的齿轮泵排量计算方法，进而将齿轮泵的齿槽有效体积以及所有齿轮轮齿的体积分别计算出来，得到了齿轮泵排量的计算原则。郜立焕等［9］在研究流量脉动产生原因中指出，齿轮泵中输出的流量随转动轴的转角按抛物线规律变化。胡昕好［10］指出，齿轮泵工作过程中的流量脉动会引起压力脉动，造成设备振动，降低系统的稳定性。周兰美［11］利用能量法计出外啮合齿轮泵齿轮变位系数对流量脉动的影响。邬自力等［12］将计算齿槽面积作为计算齿轮泵排量的核心，提出用微积分的逼近法计算齿槽面积，并利用齿部的啮合起始圆和齿顶圆作为积分的上下限，避免引入补偿系数，从而准确计算了齿槽面积。

众所周知，在齿轮设计中引入变位系数是调整齿轮中心距和轮齿强度的有效途径。在前人有关熔体齿轮泵挤出稳定性方向的研究中，关于带有变位系数的齿轮泵的性能研究较少。所以，笔者在前人研究的基础上，利用扫过面积法建立了可分析外啮合变位齿轮泵挤出性能的数学模型。并利用该模型分析了高度变位、角度变位正传动和角度变位负传动等几种模式下齿轮泵的变位系数对齿轮泵产量和挤出稳定性的影响。研究中还综合考虑了齿轮齿数的影响。

1　数学模型

齿轮泵齿轮啮合几何关系及啮合线构造过程如图1所示。在确定两齿轮中心距后，在两齿轮中心点O1和O2位置分别作两齿轮的基圆Rj1和Rj2。过两基圆的公法线并外切于两基圆的切线即为啮合线，啮合线与两齿轮中心连线的交点为节点C，节点C的圆周速度方向与啮合线之间所夹的锐角为啮合角。节点绕各自中心旋转而形成节圆R1和R2。在两齿轮中心点位置分别作两齿轮的齿顶圆Ra1和Ra2。齿顶圆与啮合线相交分别得到齿轮进入啮合点C1和齿轮脱离啮合点C2。两圆心到C1的距离即为啮合半径Rc1和R′c2，两圆心到C2的距离即为啮合半径Rc2和R′c1。C到C1的距离为f1，C到C2的距离为f2，通常将啮合起点到节点的距离f1定为负值，啮合止点到节点的距离f2定为正值。

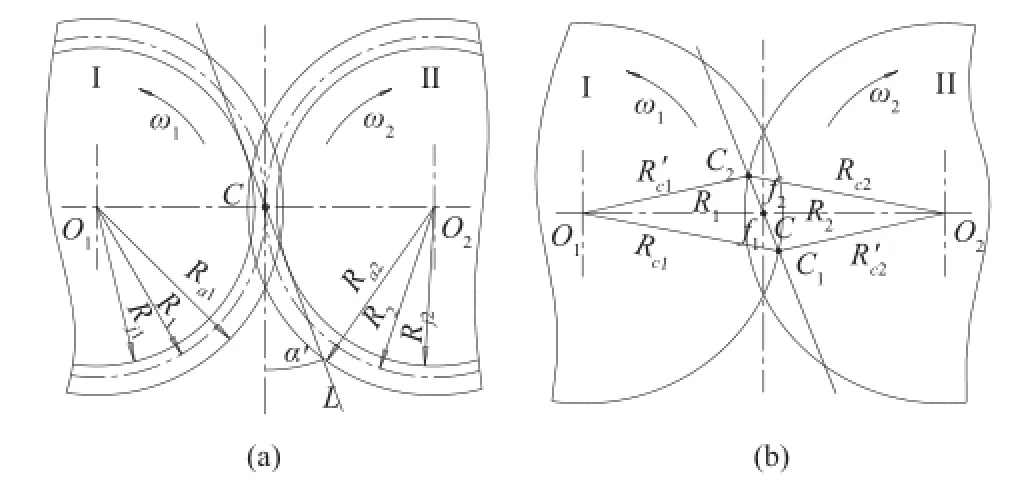
图1　齿轮泵齿轮啮合几何关系及啮合线的构造

在分析啮合线的基础上，根据齿轮啮合的基本定律，利用扫过面积法［13-14］得到在齿轮I转角dφ1内，排料腔的体积为：

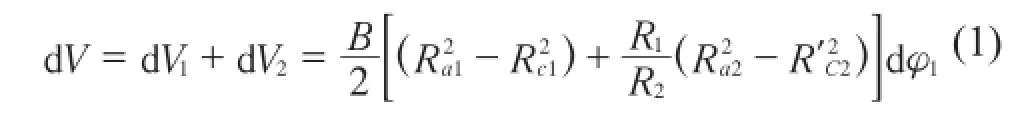
式中：B——齿轮的宽度，mm。

结合图1b，根据三角函数关系式可知外啮合变位齿轮齿轮泵的瞬时流量计算公式：

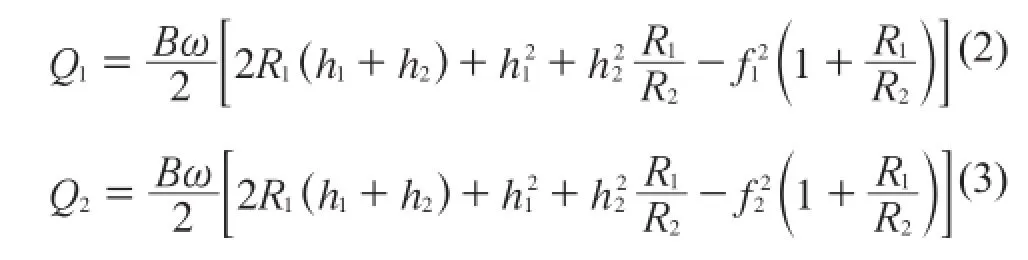
式中：ω——齿轮的角速度，rad/s；

h1，h2——齿轮I和齿轮II的齿顶高，mm。

当两啮合齿轮开始排料（啮合结束）时，瞬时流量最小：

当f1和f2都为零时（即啮合点与节点重合）时，瞬时流量最大：

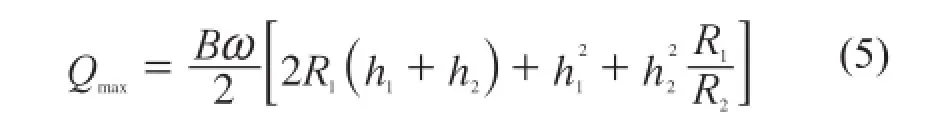
式中：ω——齿轮的角速度，rad/s；

B——齿轮的宽度，mm；

h1，h2——齿轮I和齿轮II的齿顶高，mm。

式（2）、（3）和（5）中齿轮泵相关参数计算如下：

式中：m——齿轮模数，mm；

一组科学数据显示：1991年夏季，北冰洋海冰的面积为1400万平方公里；2007年大洋海冰面积缩小速度尤为明显，面积为600多万平方公里。最近一次北冰洋大面积“缩水”发生在去年，大洋海冰面积仅余341万平方公里。全球许多科学家的气温模型都预测，2030年前后，夏季北冰洋的海冰将全部融化。

a——标准中心距，mm；

x1和x2——齿轮I和齿轮II的变位系数。

两齿轮啮合半径Rc1和Rc2的计算公式分别为：

2　流量不稳定性指标

式中：q——齿轮泵的排量，mm3/r；

n——齿轮泵的转速，r/min。

3　结果与分析

对于高度变位齿轮传动来说，两齿轮变位系数x1= -x2。虽然中心距与标准齿轮传动一致，但由于引入变位系数使得齿轮轮廓发生变化，其实际啮合过程也发生变化，导致齿轮泵输送性能发生变化。对于角度变位齿轮来说，变位后两齿轮中心距发生了变化，同时啮合角与中心距有关，变位系数与啮合角有关，所以角度变位同样会影响齿轮啮合过程，从而影响齿轮泵的输送能力和挤出稳定性。研究中齿轮泵的基本参数见表1。

表1　齿轮基本参数

3.1高度变位齿轮对挤出稳定性的影响

齿轮泵齿轮高度变位系数设置如表2所示。图2为齿轮高度变位系数对平均流量和流量脉动率δ的影响。研究中同时考虑了中心距不变的情况下齿数增加（模数减小）的影响。

表2　高度变位齿轮变位系数

图2　齿轮I变位系数x1对和δ的影响

从图2可以看出，在齿数不变的条件下，随着齿轮I高度变位系数x1增大（齿轮II高度变位系数x2减小），平均流量逐渐减少，脉动率逐渐增加。可见，高度变位后的齿轮泵稳定性能变差。此外，高度变位齿轮的中心距不变，齿数增加而齿槽容积减小，导致齿轮啮合周期齿槽容积的变化减小，所以平均流量减少的同时，流量脉动减小。挤出稳定性得到提高，但产量降低。

3.2角度变位齿轮正传动对挤出稳定性的影响

角度变位正传动两齿轮变位系数设置如表3所示。图3示出该条件下总变位系数x∑对和δ的影响。图3中，相同齿数条件下，与标准齿轮相比，角度变位齿轮正传动的流量脉动率明显增加。但随着齿轮I和齿轮II变位系数之和x∑增大，虽然δ呈现增加的趋势，但变化相对较小。同时，还可以观察到，随着x∑的增大，齿轮泵的呈线性增加趋势，这是因为齿槽容积随着x∑增大而增加。在表1所列的几种齿轮参数中，随着齿数增加，齿槽容积减小，导致齿轮泵平均流量减少，但可以在一定程度上提高挤出稳定性。随着变位系数增加，虽然产量增加，但是稳定性有所下降。从轮齿的力学性能角度来看，其齿高减小，有利于提高轮齿强度。角度变位齿轮正传动可用于高黏度物料挤出工况。

表3　角度变位齿轮正传动变位系数

图3　角度变位齿轮正传动总变位系数x∑对和δ的影响

3.3角度变位齿轮负传动对挤出稳定性的影响

角度变位负传动中两齿轮变位系数如表4所示。图4示出该条件下总变位系数x∑对和δ的影响。从图4可以看出，相同齿数条件下，与标准齿轮相比，角度变位齿轮负传动的流量脉动率明显增加，而且随着x∑增大，流量脉动率逐渐减小。与此同时，从图4中还可以看出，挤出产量也随着x∑的增大而提高。此外，齿数增加（依托表1中齿轮参数），平均流量减小，流量脉动率减小。故可以推断，标准齿轮有利于提高齿轮泵的挤出产量和挤出稳定性。随着变位系数的绝对值增加，虽然产量和稳定性都有所下降，但从轮齿的力学性能角度来看，齿高减小有利于提高轮齿强度。角度变位齿轮负传动也可在高黏度物料挤出的工况下使用。

表4　角度变位齿轮负传动变位系数

图4　角度变位齿轮负传动总变位系数x∑对和δ的影响

4　结论

利用建立的齿轮泵瞬时流量公式，分析了三种变位情况下齿轮泵挤出产量和挤出稳定性的变化情况。对于高度变位齿轮来说，变位系数的增大导致齿轮泵平均流量减少，而且挤出稳定性变差。对于角度变位正传动来说，总变位系数增大导致齿轮泵平均产量增加，但挤出稳定性变差。当采用角变位负传动时，总变位系数增大，不仅平均产量呈现增大趋势，而且齿轮泵的挤出稳定性得到提高。故可以推断，标准齿轮有利于提高齿轮泵的挤出稳定性，角度变位齿轮有利于提高齿轮强度，可在高黏度物料挤出的工况下使用。

［1］ 甘学辉，吴晓铃，侯东海.全齿廓啮合斜齿齿轮泵流量脉动特性［J］.石油化工设备，2002，31（5）：8-10. Gan Xuehui，Wu Xiaoling，Hou Donghai. Flow pulse property of whole profile mesh helical gear pump［J］. Petro-Chemical Equipment，2002，31（5）：8-10.

［2］ 赵亮，王东屏，任喜岩.斜齿齿轮泵流量脉动特性分析［J］.大连铁道学院学报，2001，22（4）：25-28. Zhao Liang，Wang Dongping，Ren Xiyan. Flow pulse analysis of helical gear pump［J］. Journal of Dalian Railway Institute，2001，22（4）：25-28.

［3］ 苏欣平，郭仲，魏晓光，等.基于MATLAB的复合齿轮泵流量脉动特性的仿真［J］.中国工程机械学报，2009，7（3）：343-345. Su Xinping， Guo Zhong， Wei Xiaoguang， et al. MATLAB-based flow pulsation characteristic simulation on compound gear pumps［J］. Chinese Journal of Construction Machinery，2009，7（3）：343-345.

［4］ 李秀明.高粘度齿轮泵特性分析及齿轮参数优化［D］.郑州：机械科学研究院，2002. Li Xiuming. Property analysis of high viscidity gear pump& optimization of the gear parameters［D］. Zhengzhou：Mechanical Engineering Research Institute，2002.

［5］ 司健.外啮合齿轮泵的泵齿轮最佳参数的研究及CAD［D］.北京：清华大学，2002. Si Jian. Study about the optimum value of external spur pump gear and its CAD［D］. Beijing：Tsinghua University，2002.

［6］ 邹旻，祝海林，李迎.齿轮变位后齿轮泵的排量计算［J］.机床与液压，2002 （3）：23-25. Zou Min，Zhu Hailin，Li Ying. Displacement calculation for gear pump with corrected gears［J］. Machine Tool & Hydraulics，2002（3）：23-25.

［7］ 杨国来，刘志刚，杨长安，等.内啮合齿轮泵齿轮变位系数对流量脉动的影响［J］.机床与液压，2008，36（11）：60-61. Yang Guolai，Liu Zhigang，Yang Changan，et al. Effect of internal gear pump modification coefficient on flow pulsation［J］. Machine Tool & Hydraulics，2008，36（11）：60-61.

［8］ 宗光涛，周志鸿，白忠飞，等.齿轮泵排量计算方法研究［J］.液压气动与密封，2009，29（3）：32-34. Zong Guangtao，Zhou Zhihong，Bai Zhongfei，et al. Study of displacement calculation for gear pump［J］. Hydraulics Pneumatics & Seals，2009，29（3）：32-34.

［9］ 郜立焕，唐晓阳，李言芝，等.齿数对齿轮泵流量脉动特性影响的分析［J］.机床与液压，2011，39（6）：71-72. Gao Lihuan，Tang Xiaoyang，Li Yanzhi，et al. Influence of teeth number on flow pulsation characteristic of gear pump［J］. Machine Tool & Hydraulics，2011，39（6）：71-72.

［10］ 胡昕好.大流量外啮合齿轮泵的理论研究［D］.阜新：辽宁工程技术大学，2011. Hu Xinhao. The theory research of big flow external gear pump［D］. Fuxing：Liaoning University of Project Technology，2011.

［11］ 周兰美.外啮合齿轮泵变位系数对流量脉动的影响［J］.煤矿机械，2011，32（1）：110-111. Zhou Lanmei. Influence of modification coefficient of flow pulsation of external gear pump［J］. Coal Mine Machinery，2011，32（1）：110-111.

［12］ 邬自力，郭威.基于齿形分析的变位齿轮泵排量计算方法［J］.中国水泥，2015（7）：90-92. Wu Zili，Guo Wei. The calculation method of displacement of modified gear in gear pump based on tooth profile［J］. China Cement，2015（7）：90-92.

［13］ 喻开清.齿轮泵流量脉动分析与优化设计［D］.哈尔滨：哈尔滨工业大学，2006. Yu Kaiqing. Flow rate pulsation analysis and optimal design of gear pump［D］. Harbin：Harbin Institute of Technology，2006.

［14］ 聂一彪.大排量齿轮泵的结构及性能优化研究［D］.广州：广东工业大学，2007. Nie Yibiao. Study on the structure and performance optimization of the large displacement gear pump［D］. Guangzhou：Guangdong University of Technology，2007.

［15］ 刘茜.外啮合齿轮泵的瞬时流量及脉动特性研究［J］.机械传动，2012（6）：17-21. Liu Qian. Study on instantaneous flow and pulsation characteristic of the external gear pump［J］. Mechanical Drive，2012（6）：17-21.

［16］ 刘玉兰，刘忠朝.低脉动低噪音齿轮泵的研究［J］.西安矿业学院学报，1990，10（2）：85-92. Liu Yulan，Liu Zhongchao. Study on low-flux pulse and low noise of the gear pump［J］. Journal of Xi'an Mining Institute，1990，10（2）：85-92.

Effect of Modification Coefficient on Extrusion Stability of Polymer Melt Gear Pump

Fan Kebin， Bi Chao
（College of Mechanical and Electrical Engineering， Beijing University of Chemical Technology， Beijing 100029， China）

Aiming at the problem of micro fluctuation which was brought by gear pump，due to the variation of the tooth space volume in the meshing process of two gears，a flow calculation model of gears with profile modification was established based on swept area method herein. Based on the model，the effect of modification coefficient on extrusion stability when the number of teeth increased was analyzed for the situations of addendum modification， positive angle modification and negative angle modification，using average flow rate and flow pulsation as evaluating indexes.

gear pump；extrusion stability；modification coefficient

TQ320

A

1001-3539（2016）06-0072-04

10.3969/j.issn.1001-3539.2016.06.016

联系人：樊柯彬，硕士研究生，主要研究方向为齿轮泵的挤出稳定性

2016-03-23