数据挖掘技术在电力设备故障诊断中的应用

杨超，张霖

(贵阳供电局，贵州　贵阳　550002)



数据挖掘技术在电力设备故障诊断中的应用

杨超，张霖

(贵阳供电局，贵州贵阳550002)

电力设备运行状态信息具有海量、复杂性以及不完整的特点，给设备故障诊断带来了不小的困难。本文提出一种将粗糙集理论与朴素贝叶斯相结合的数据挖掘方法，通过粗糙集求取故障诊断最小属性约简集，并在此基础上利用朴素贝叶斯计算设备发生各种故障的概率，从而得出诊断结果。最后进行了变压器故障实例分析，诊断结果证明该方法的正确性和有效性。

电力设备；数据挖掘；故障诊断；粗糙集；朴素贝叶斯

1　引言

故障诊断是根据设备运行状态信息查找故障源，并确定相应决策的一门综合性的新兴科学。电力设备故障诊断技术的应用，使设备维修由传统的计划维修逐步过渡到状态维修，减少了事故停电损失，提高了电网供电可靠性，具有重要的经济和社会效益。随着工业和科学技术的迅速发展，SCADA、生产管理系统以及设备在线监测系统等的广泛应用,与设备状态相关的各种数据呈爆炸性增长态势,数据之间的相互关系更加趋于复杂化，传统的分析统计手段已难以满足要求,需要运用新方法来挖掘更深层次的规律,确定设备是否存在异常或故障、故障的部位以及故障恶化的趋势，以便给出更快、更有效的维修决策支持。数据挖掘的出现引起了电力工作者的广泛关注[1]。

数据挖掘是从大量的、已有数据(数据库或数据仓库)中发现未知的、具有潜在应用价值的信息或模式,被广泛地应用于金融、市场营销、过程优化控制、电力系统等各个领域[2]。在数据挖掘的分类过程中所使用的一些方法有贝叶斯分类器,神经网络分类方法,K-最临近方法,遗传算法,模糊集合还有粗糙集等方法。他们都有各自的特点,将各个方法相融合,取长补短,有机高效得整合在一起是当前探索的一个热点。

本文从粗糙集和朴素贝叶斯两种方法具有的优势互补性出发,针对电力设备故障数据中通常存在信息不完整或错误等问题,提出了一种基于粗糙集和朴素贝叶斯的数据挖掘方法,用基于互信息的属性约简算法提取出最小属性约简集,最后根据约简的决策表建立朴素贝叶斯模型,计算区域故障概率,得出诊断结果。

2　数据挖掘相关理论

2.1基于粗糙集的属性约简

粗糙集理论是由波兰的Z.Pawlak教授于1982年提出的一种处理模糊和不确定性问题的新型数学工具，它能有效地分析和处理不精确、不一致、不完整等不完备性数据，通过发现数据间隐藏的关系，揭示潜在的规律，从而提取有用信息，简化信息的处理[3]。

粗糙集把客观世界抽象为一个信息系统S=(U,A,V,f),其中U为对象的非空有限集,称为论域；A为属性的非空有限集,V为属性A的值域；f:U×A→V是信息函数,即a∈A,x∈U,f(x,a)∈Va。若A可由条件属性C和决策属性D表示,即A=C∩D,C∩D=φ,则称该知识表达系统为决策表。

根据信息论可以定义知识的熵与条件熵的概念，知识(属性集合)P的熵H(p)定义为：

(1)

知识(属性集合)Q(U|IND(Q))={Y1，Y2，…，Ym}相对于知识(属性集合)P(U|IND(P))={X1，X2，…，Xm}的条件熵H(Q|P)定义为:

(2)

其中:p(Xj|Xi)=|Yj∩Xi|/|xi|,(i=1,2,…,n;j=1,2,…,m)

则知识P、H之间的互信息可定义为:

(3)

式中p表示求概率。

原始决策表中并非所有的条件属性都是必要的，有些是多余的，去除这些属性不会影响原有的表达效果。因此，采用粗糙集描述知识，通过去除冗余的条件属性求取约简可以实现知识的简化，将一个复杂的决策表约简为不含多余属性并保证分类正确的最小条件属性决策表。基于粗糙集的属性约简算法具体步骤如下：

步骤1 计算决策表T中条件属性C和决策属性D的互信息I(D,C)=H(D)-H(D|C)；

步骤2 计算条件属性的简约即从决策表中删去一些冗余的列；

步骤3 删去重复的行即删除重复对象；

步骤4消去每一决策规则中的冗余属性。

约简后的决策表是一个不完全的决策表，它仅包含那些在决策时所必需的条件属性值，但它具有原始知识系统的所有知识。

2.2朴素贝叶斯分类原理

贝叶斯网络，又称因果网络、信度网络，是一种带有概率注释的有向无环图(DAG)。它以有向图的形式表示随机变量间的因果关系，并通过条件概率将此关系量化。朴素的贝叶斯分类方法是贝叶斯方法中实用性很高的一种学习方法，以概率密度函数为基础,描述分类系统中条件属性和分类属性之间的映射关系,相比于其他算法,具有出错率最小的特点[4]。

朴素贝叶斯分类器假定属性变量间相互类条件独立,每个属性节点Xi只与类节点C相关联。令U={X1,X2,…,Xn,C}是离散随机变量的有限集，其中X1,X2,…,Xn是属性变量，类变量C的取值范围为{c1,c2,…,cm} ，xi是属性Xi的取值。假设给定一个故障样本X={x1,x2,…,xn}，此样本属于故障类ck的概率由贝叶斯定理表示为：

(4)

式中P(ck)为ck类的先验概率,即根据以往的数据分析得到的类ck发生的概率;P(x1,x2,…,xn|ck)为类ck的后验概率,即得到某些信息后重新修正的类ck发生的概率,后验概率反映了样本数据对类ck的影响。

由于P(X)对于所有故障类均为常数,因此只需P(X|ck)P(ck)最大即可。其中先验概率可通过式(5)求得：

P(ck)=Nck/N

(5)

上式中k=1,2,…,m；N为训练样本总数；Nck为训练样本中故障区域类ck出现的样本个数。朴素贝叶斯算法假定各个属性x1,x2,…,xn之间互相独立,只与故障类C相关,则后验概率可由化简公式(6)求得：

(6)

其中概率P(xi|ck)可由训练样本计算,即

(7)

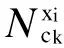
(8)

通过以上公式可求得故障样本属于类变量C中某个故障类ck的概率P(ck|X),若属于某个故障类的此概率值最大,则该故障样本就属于此故障类。

3　基于粗糙集和朴素贝叶斯的电力设备故障诊断

粗糙集理论的主要优势之一在于它不需要任何预备的或额外的有关数据信息,完全依据数据驱动进行知识发现。但其局限在于当把实时故障信息与规则库中的规则进行匹配得出诊断结果时,若故障信息不完备,诊断结果极易出错,且诊断耗时长。朴素贝叶斯可以利用概率理论处理故障信息与规则库(训练样本)之间的这种不确定性,同时当规则库较大时,概率的计算要比规则匹配搜索速度快。但是贝叶斯方法在使用过程中主要存在两个方面的限制:一是先验概率定义困难;二是条件属性的独立假设问题。

本文提出结合粗糙集与朴素贝叶斯的电力设备故障诊断方法。该方法通过粗糙集约简参与分类的属性个数,得到相互独立的核心属性,然后基于最小属性约简集进行朴素贝叶斯方法的分类知识挖掘,使贝叶斯方法可以适用于更大的范围。算法流程如图1所示。

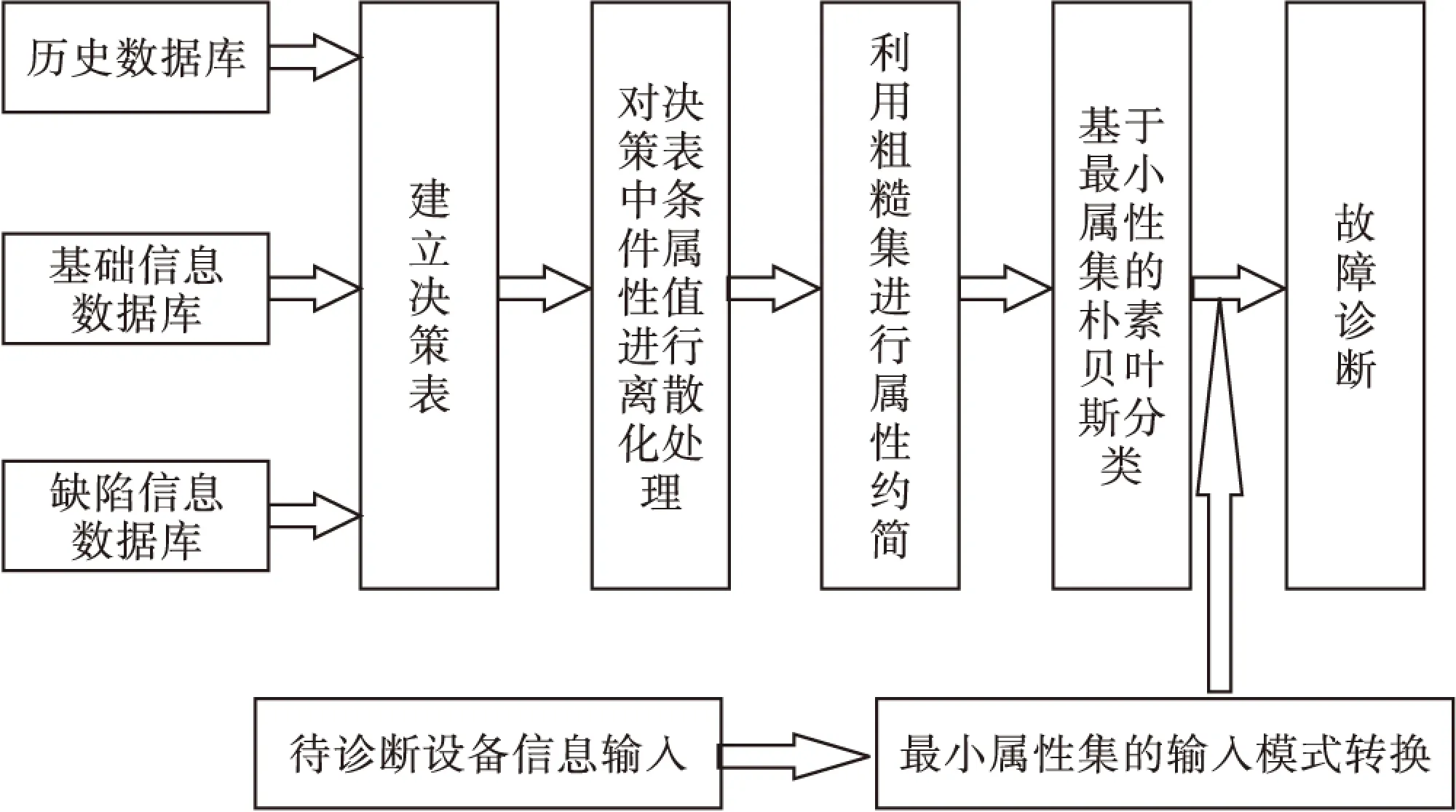
图1　故障信息挖掘实现框图

下面以变压器故障诊断为例说明数据挖掘过程,其中定义条件属性C为征兆集合，决策属性D为故障集合。本文从变压器运行情况和相关文献中收集到100例变压器故障样本进行了分析研究[5-6]，给出了征兆集合C(表1)和故障集合D(表2)，并利用公式(5)计算出各故障的先验概率。

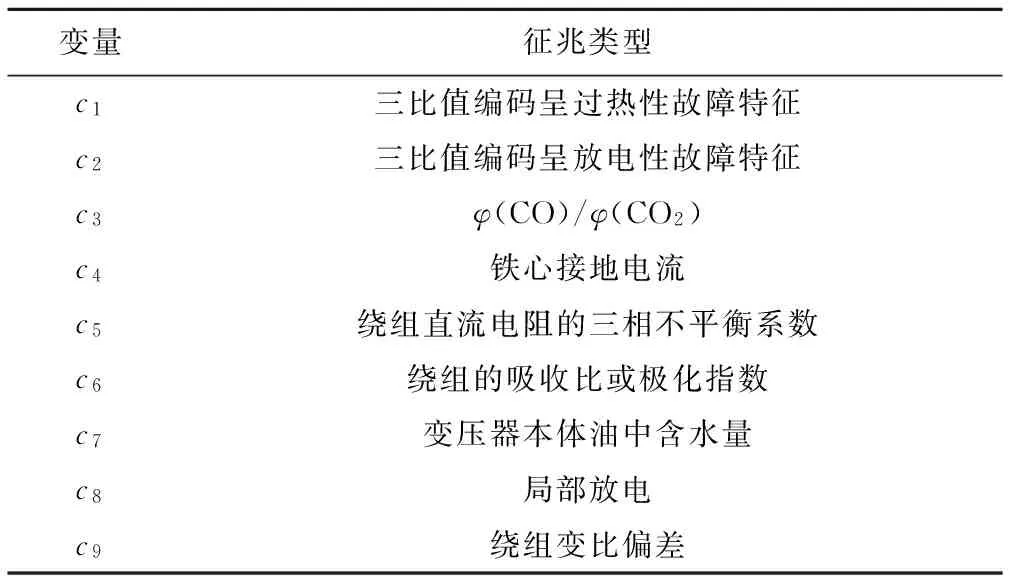
表1　征兆集合C列表

表2　故障集合D列表

根据上文公式(1)～(3)，计算得到故障集合与征兆集合的互信息I，如表3所示：

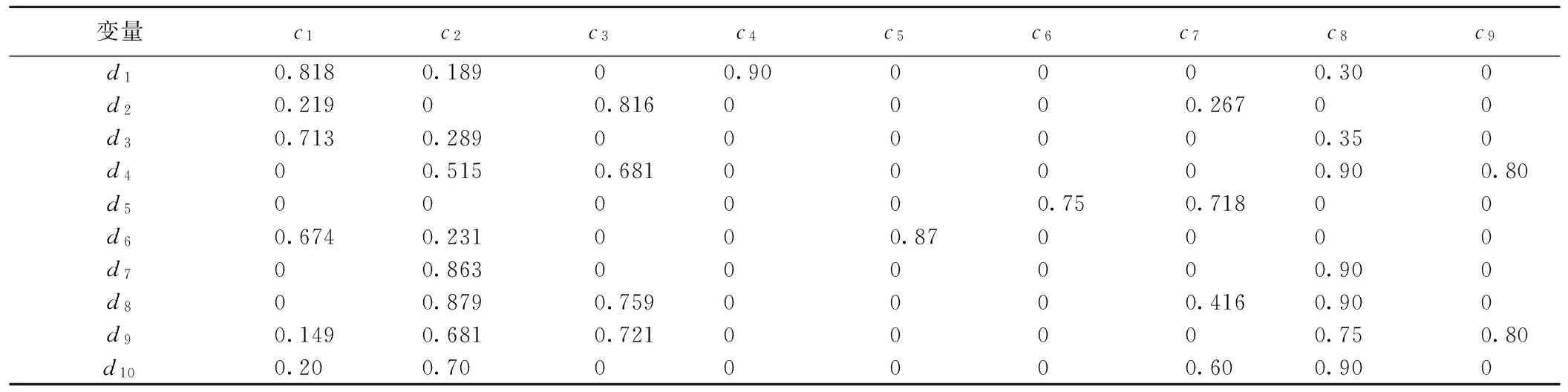
表3　故障集合与征兆集合的互信息I

从粗糙集的观点，表3是一张决策表，条件属性为征兆集合{c1，c2，…,c9}，结论属性为故障类型{d1，d2，…,d10}。但表中数据为连续值，即各属性视为连续属性，按粗糙集理论须将其离散化，因此本文以互信息大于0.5时量化为2，互信息小于0.5时量化为1，互信息等于0时量化为0这种规则将每个条件属性离散化，直观上可以理解为该征兆引起此类故障的概率较大、较小或几乎没有。经上述加工处理后，得到表4所示的电力变压器故障诊断决策表。

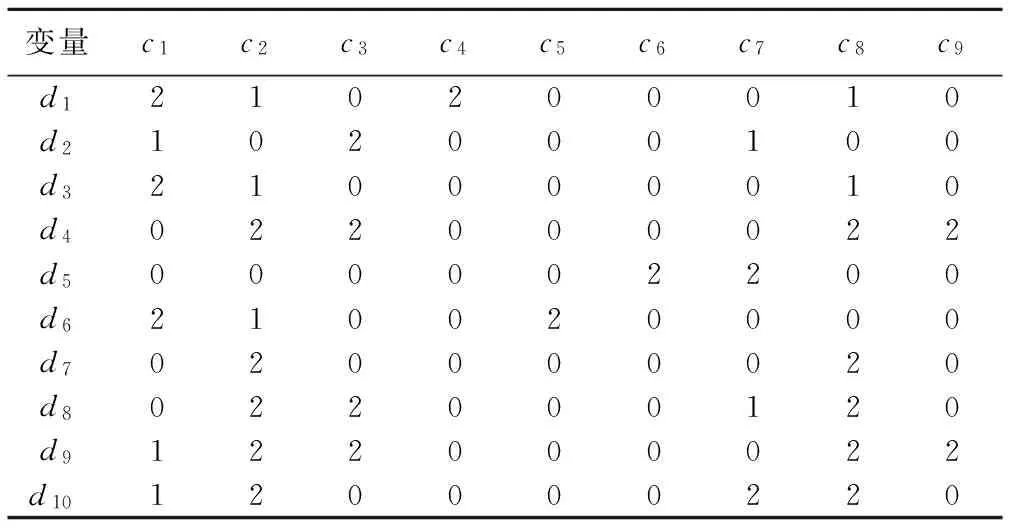
表4　故障诊断决策表

对故障决策表进行约简，约简时选择互信息最小的条件属性,约简后的属性是相互独立的,满足朴素贝叶斯算法的约束条件。这里选择的最小属性集分别为{c1，c2，c3，c5,c7}，{c1，c3，c4，c5,c7}，{c1，c3，c4，c7,c8}，{c1，c4，c5，c7,c9}和{c1，c4，c7，c8,c9}。而其中的属性集{c1，c3，c4，c5,c7}和{c1，c4，c5，c7,c9}中有一个决策属性对应的条件属性全为0，故删除。考虑到征兆获取的难易，选择属性集{c1，c3，c4，c7,c8}作为变压器故障诊断决策最小约简表，如表5所示。

4　变压器故障诊断实例

某变压器型号为SFSZ8-50000/110，运行中油色谱分析气体组分如表6所示。

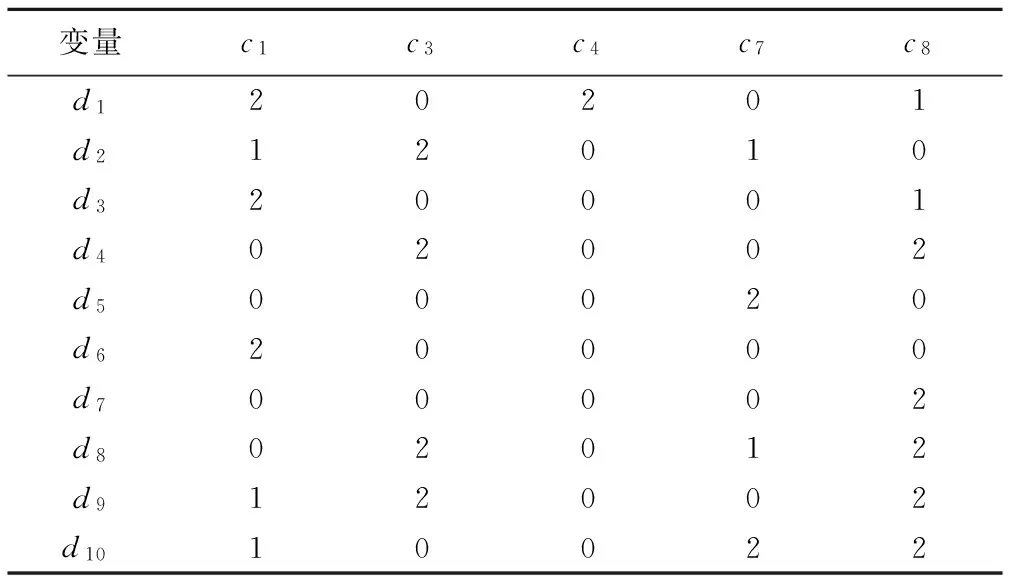
表5　最小故障诊断决策表

表6　变压器各特征气体浓度(μl/L)

分析各特征气体的比值如下：φ(CH4)/φ(H2)=2.64，φ(C2H2)/φ(C2H4)=0.002，φ(C2H4)/φ(C2H6)=5.32，三比值编码为022，属高温过热性故障特征；铁心接地电流为1.378A，属性值存在异常；另外φ(CO)/φ(CO2)=0.32，变压器油中含水量为17mg/L ,局部放电量均在正常范围内。

对于上面给定的故障信息C={c1，c3，c4，c7,c8}，应用公式(4)和(6)进行计算，得到各故障发生的概率结果如表7。

表7　各种故障发生的概率

由表7可知，故障类d1存在的概率最大，即铁芯多点接地的可能性最大，且明显大于其他故障原因，因此故障诊断结果为铁芯多点接地故障。而本台变压器实际吊罩结果为：变压器内部存在铁屑残渣，这些铁屑残渣在变压器运行时，由于铁芯磁场的影响吸附在铁芯上，造成铁芯环流过热或铁屑多点接地。对变压器故障信息挖掘得到诊断结果，与实际情况相吻合。

5　结论

本文将先进的数据挖掘技术应用于电力系统，提出一种基于粗糙集与朴素贝叶斯的电力设备故障诊断方法。利用粗糙集信息表约简技术来实现对专家知识的简化与故障特征的压缩，可以有效降低问题解决的复杂性与故障特征获取的难度；同时利用朴素贝叶斯模型实现概率推理，便于描述故障特征的变化及对设备故障原因的快速分析。故障实例分析表明，文中所提出的方法可以有效进行不确定性推理，减少诊断信息的冗余性，诊断结果证明了本方法的有效性。

[1](美)韩家炜，等.数据挖掘：概念与技术[J].3版.机械工业出版社，2012.

[2]陈星莺,张晓花,翟峰,等.数据挖掘在电力系统中的应用综述[J].电力科学与技术学报,2007,22(3):51-56.

[3]张文修.粗糙集理论与方法[M].北京：科学出版社，2001.

[4]林士敏，田凤占，陆玉昌.贝叶斯网络的建造及其在数据采掘中的应用[J].清华大学学报(自然科学版)，2001，41(1)：49-52.

[5]杨莉，尚勇，周跃峰,等.基于概率推理和模糊数学的变压器综合故障诊断模型[J].中国电机工程学报，2000，20(7)：19-23.

[6]王楠，律方成，刘云鹏,等.基于决策表约简的变压器故障诊断Petri网络模型及其应用研究[J].电工技术学报，2003，18(6)：88-93.

Application of Data Mining Technology in Power Equipment Fault Diagnosis

YANGChao,ZHANGLin

(Guiyang Power Supply Bureau,Guiyang 550002，China)

The data of the power equipment is massive,complex and incomplete,which creates no small difficulty for equipment fault diagnosis.This paper presents a data mining method which combines the rough set theory with the Naive Bayesian classification.The minimum attribute reduction set is first extracted by using the rough set method,then the probability of various faults can be calculated with the naive Bayesian classification method.Finally,the correctness and effectiveness of this method are validated by the result of practical fault diagnosis examples to the transformer.

power equipment;data mining;fault diagnosis;rough set theory;Naive Bayesian

1004-289X(2016)02-0083-04

TM76

B

2015-03-09

杨超(1981-)，男，高级工程师，硕士，主要从事高压绝缘监督工作；

张霖(1976-)，男，高级工程师，硕士，主要从事高压绝缘监督工作。