带权决策表的属性约简

李 旭，荣梓景，任 艳

1.新疆财经大学 信息管理学院，乌鲁木齐830012

2.北京语言大学 信息科学学院，北京100083

1 引言

粗糙集理论是由波兰学者Pawlak[1]提出的，是一种处理不确定、不一致和模糊问题的数据分析工具。近年来，粗糙集理论的研究成果丰硕，在机器学习、数据挖掘、决策支持与分析、医疗卫生服务、物联网等诸多领域中，取得了成功应用。属性约简是粗糙集研究的重要内容之一，其主要思想就是根据特定规则要求，删除冗余属性，得到知识分类最小属性子集。

目前，属性约简已取得了大量的理论研究成果。将决策表和不同应用背景相结合，研究人员提出了正域约简[2-3]、变精度约简[4-5]、分配约简[2，6]、覆盖约简[7-8]、分布约简[9]、局部约简[10-12]等多种类型的约简。已有的研究已通过容差关系[13]、量化容差关系[14]、限制容差关系[15]等拓展了正域约简的应用范围。Liu[16]在一致决策表和不一致决策表上提出了一般关系，从而推广了二元关系。文献[11]在一般关系下，提出了上下近似的概念，并给出了严格证明。在决策表中，正域约简[3]研究已取得重要进展。现阶段一般通过启发式约简算法[17-19]和基于辨识矩阵[20-21]的算法等两种方法进行属性约简。虽然启发式约简算法能够快速计算约简，但不能得到所有约简。基于辨识矩阵的算法数学论证严格，目前仍是得到所有约简的最好方法，本文中涉及的约简均是通过辨识矩阵的方法得到的。近似分类精度[2]也称分类精度，其表达了当使用条件属性集对对象进行分类时，可能的决策中正确决策的百分比。文献[22]研究了区分能力和分类能力之间的关系，更细致地描述了近似分类概念。文献[23]提出了求解近似质量属性约简的迭代约简算法。文献[24]以属性重要度来刻画近似精度差，通过启发式约简算法得到近似精度约简，然而该方法不能得到所有约简。目前，基于辨识矩阵讨论分类精度约简的研究讨论较少。

带权决策表是一种特殊形式的决策表。由论域、条件属性集、决策属性集等要素构成决策表的基础上，通过增加一列元素（权）来形成带权决策表。在不同领域背景下，通常情况下决策表结构不能够很好地表示实际情况。例如，在大型机械设备故障诊断中，机械设备中的各子系统指标构成条件属性集，不同的故障结果构成决策属性集。当发生某种机械故障时，把各子系统中指标参数出现的相同频次作为权值，来描述某种机械故障的样本数量。当发生某种机械故障时，通过构建带权决策表可以为专家分析研究问题提供理论依据。因此，关于带权决策表的属性约简在故障诊断、医疗诊断等领域具有比较重要的现实意义。

基于上述分析，关于带权决策表的属性约简研究讨论相对较少。因此，本文提出了在带权决策表中，通过计算对象权值比的方法得到正域，从而进行正域约简，该算法的时间复杂度优于文献[3]给出的正域约简算法的时间复杂度。同时，本文提出了近似分类精度约简的算法，并进行了严格的理论证明。

2 基本概念

为便于进一步对决策表的属性约简进行研究，本章将介绍关于决策表的相关概念、正域约简及其对应的辨识矩阵。

在粗糙集模型中，当研究对象是一个二元信息表，称其为信息系统。设(U,C)是信息系统[1]，若B⊆C，等价关系，其中，a(x)表示对象x在a上的属性值，称RB是U上的等价关系[1]。若关系R是U上的等价关系时，R在U上具有自反性，对称性和传递性。记[x]B是RB在U上的等价类。若y∈[x]B时，恒有( x,y)∈RB。若信息系统中属性集是由条件属性集C和决策属性集D构成的，称其为决策表，记为(U,C⋃D)。定义1[1-2]设(U,C)是信息系统，其中U是论域，RC是由属性集C决定在U上的等价关系，若∅≠X⊆U时，关于X的上近似，下近似分别为：

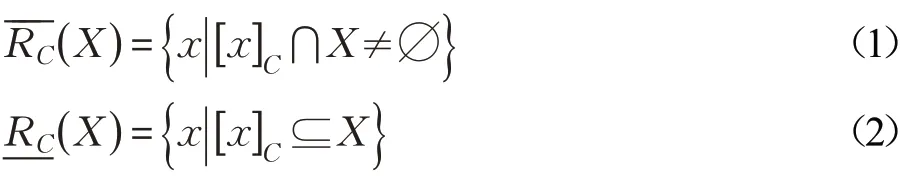
文献[11]给出了基于辨识矩阵计算上近似、下近似约简的算法，并将其推广至关系决策表中的上近似、下近似约简。

引理1[1]设(U,C)是信息系统，若RC是U上的等价关系，对于X⊆U,有，其中，～X是X的补集。

定义2设(U ,C)是信息系统，对于任意X⊆U，若B⊆C时，X关于B的正域、边界域[11]分别为：

定义3设(U,C)是信息系统，对于∅≠X⊆U，若B⊆C时，X关于属性集B的近似分类精度[2]为：，其中，||⋅表示集合的基。

定义4设(U,C⋃D)为决策表，U是论域，C是条件属性集，D是决策属性集，RC、RD分别是条件属性集，决策属性集确定的U上的等价关系，决策属性确定的商集为U/D={D1,D2,…,Dl}，正域为POSC(D)=，对于B⊆C时，若B满足下列两条件：

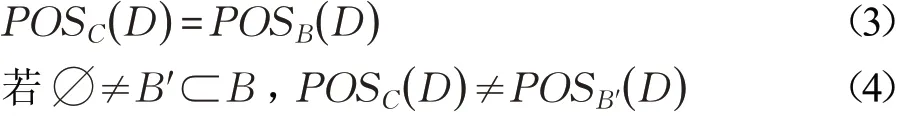
称B是C关于D的正域约简[1-2]。

正域约简相应的辨识矩阵[3]为M=( mij)s×n：

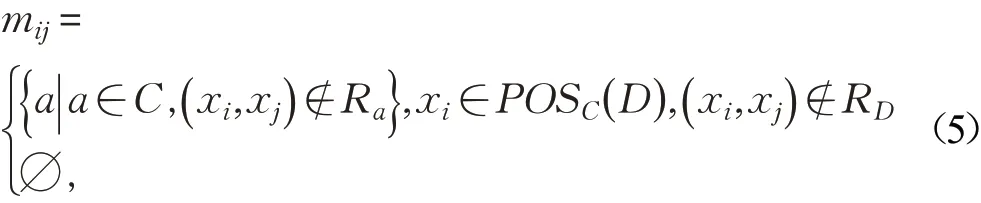
在辨识矩阵M中，s= |POSC(D )|是正域的基，n= ||U是论域中对象数。

3 带权决策表的正域约简

带权决策表是一种决策表的形式变形。把决策表中的每行均作为一条决策规则时，将出现相同决策规则的次数称为权，因而可知本文定义的权值均为正整数。考虑用权来表示决策规则在决策表中重复出现的次数，每条决策规则仅出现1次时，称决策表为带权决策表，记为(U ,C⋃D,W)。其中，U是论域，C是条件属性集，D是决策属性集，W为对象的权，RC、RD分别是条件属性，决策属性确定的U上的等价关系。现通过表1和表2来说明决策表到带权决策表的构建过程。决策表(U,C⋃D)（表1），论域U={ui|i=1,2,…,6}，条件属性集C={a1,a2,a3}，决策属性集D={d}。

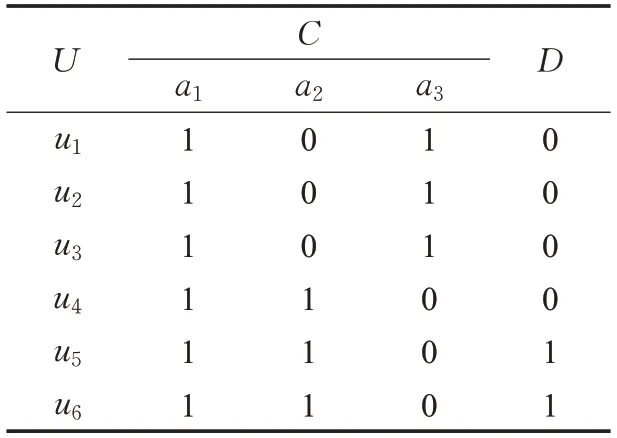
表1 决策表

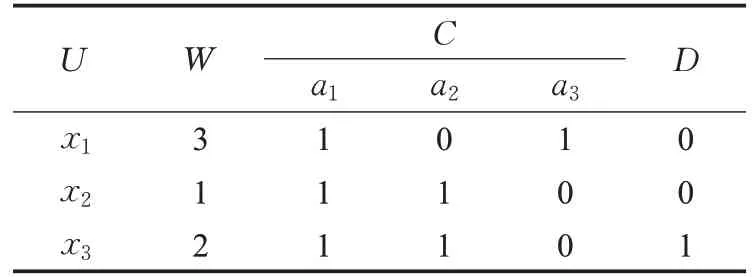
表2 经过转化的带权决策表

由带权决策表可知，若等价类[x]C中的决策规则一致时，即，则等价类[x]C必包含于正域。若等价类[x]C中的决策规则不一致，即时，则等价类[]xC任意对象必不属于正域。

对于带权决策表(U,C⋃D,W)，其正域约简对应的辨识矩阵为M′=(m′ij)s×n：

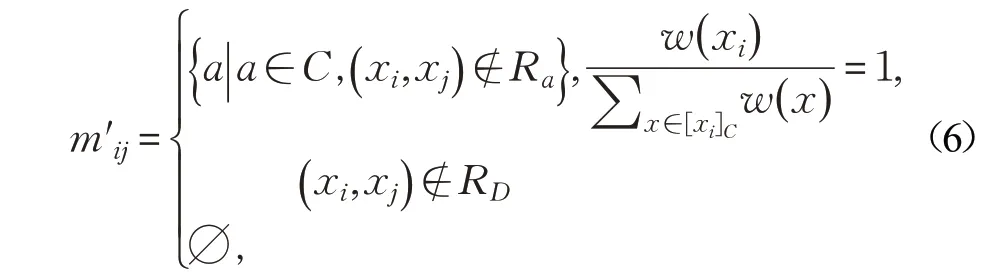
定理1设(U,C⋃D),W为带权决策表，若∅≠B⊆C时，则下列两个条件等价：

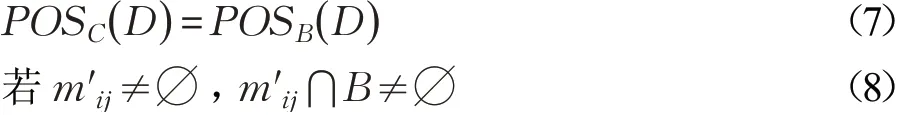
证明 (7)⇒(8)，若m′ij≠∅，有且( xi,xj)∉RD。利用反证法，m′ij⋂B=∅。对于∀a∈B,( xi,xj)∈RB。由条件（7）知：

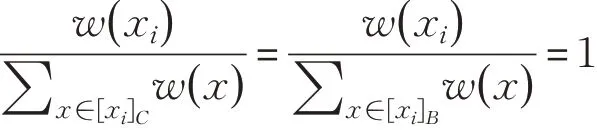
因而与( xi,xj)∉RD矛盾，得证。

(8)⇒(7)，因B⊆C，有POSB(D)⊆POSC(D)。现证POSC(D)⊆POSB(D )。由引理知m′ij≠∅，当时，需证。对于任意xj,(xi,xj)∉RD,即xj∉[]xiD。由条件（8）知m′ij⋂B≠∅，则存在Rl∈m′ij⋂B使得(xi,xj)∉RB，即

推论1设(U,C⋃D,W)为带权决策表，当B⊆C时，B是C关于D的正域约简当且仅当B为C中满足m′ij⋂B≠∅的最小子集。

算法1带权决策表中正域约简算法

输入：带权决策表(U ,C⋃D,W)。

输出：全部约简。

步骤1计算条件等价类[x]C和决策等价类[x]D。

步骤2计算正域。

步骤3构造辨识矩阵M′。

算法结束。

在通常的决策表中，基于辨识矩阵的正域约简算法需要消耗大量时间。但本章将决策表转化为带权决策表后，利用对象权值比方法，一定程度上优化了时间复杂度，能够有效提高约简的效率。本文将决策表转化为带权决策表的过程时间复杂度为带权决策表中条件类的时间复杂度为O(| C|× |U′|)。算法1在计算正域时，其时间复杂度为O(| U′|× |U′/C |)，而文献[3]中计算正域的时间复杂度为O(| U|2)，因，因此，算法1的时间复杂度优于原有算法的时间复杂度。

4 带权决策表的近似分类精度约简

在带权决策表中，近似分类精度概念描述了条件属性集对带权的对象分类时，可能的决策中正确决策的百分比，刻画为下近似基与上近似基的比值。在带权决策表(U ,C⋃D,W)中，决策属性确定的商集为U/D=，存在πD⊆U/D=，需要说明的是πD至少包含一个Di(i=1,2,…,l)。

证明 利用反证法，若E＞G或F＜H时，由条件知F≤H,E≥G，则不成立。因而E=G且F=H成立。

引理4设(U,C⋃D,W)为带权决策表，当B⊆C时，对于πD⊆U/D，的充要条件是

定义5设(U ,C⋃D,W)为带权决策表，对于πD⊆U/D，对于近似分类精度αC，若B⊆C时，若满足下列两条件：

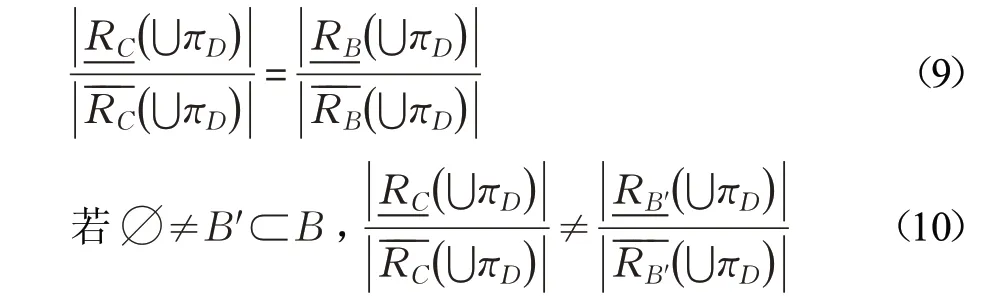
称B是关于πD的近似分类精度约简。

定理2设(U,C⋃D,W)为带权决策表，当B⊆C,πD⊆U/D时，则的充要条件是且

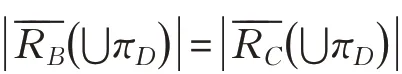
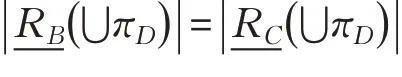
现定义辨识矩阵S=(sij)n×n如下：

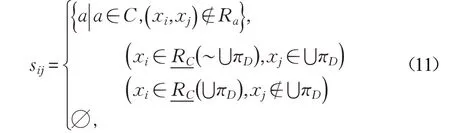
其中，n是论域的基。

定理3设(U,C⋃D,W)为带权决策表，当B⊆C时，πD⊆U/D，则下列两条件等价：

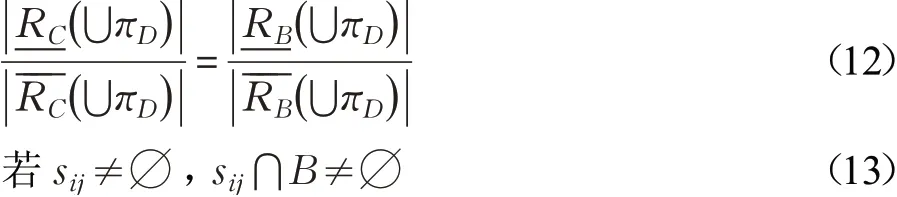
推论2设(U,C⋃D,W)为带权决策表，当B⊆C时，πD⊆U/D，B是关于πD的近似分类精度约简当且仅当B为C中满足sij⋂B≠∅的最小子集。

算法2带权决策表的近似分类精度约简算法

输入：带权决策表(U ,C⋃D,W)。

输出：全部约简。

步骤2构造辨识矩阵S。

算法结束。

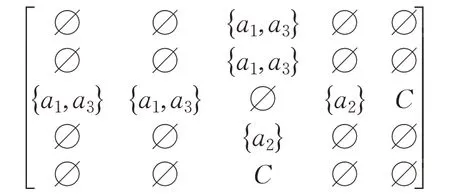
由该辨识矩阵得辨识函数为f=(a2)( a1+a3)，得析取范式为f=( a1a2)+( a2a3)，得约简为{a1a2}和{a2a3}。

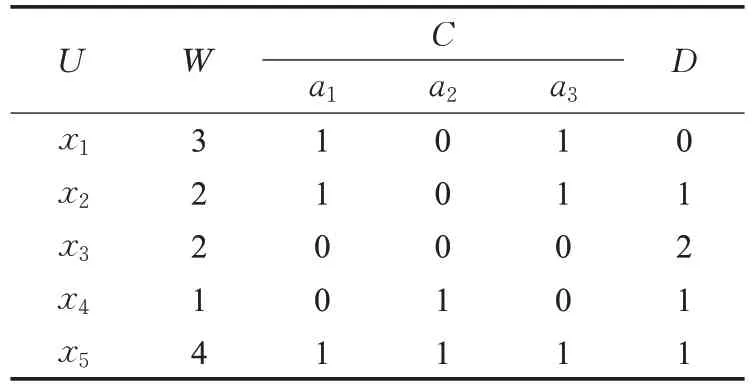
表3 带权决策表

5 实验分析

带权决策表中，针对正域约简和近似分类精度约简，本章通过实验对提出的算法进行了验证。现从UCI数据集中选取Iris，Wine，Statlog（Heart）等3个数据集（表4），来说明算法的有效性和可行性。程序运行环境：Intel®CoreTMi5-2440 CPU 3.10 GHz，Windows10 64 bit，算法为Python代码实现。

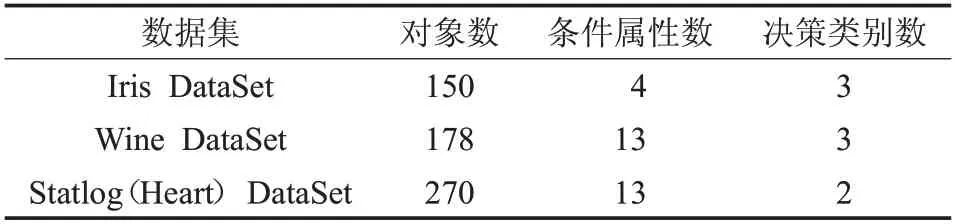
表4 数据集的有关信息

表5中，算法1和文献[3]中提出的算法（记为GPAR算法）对比说明，两者所得约简相同，同时相较于后者，算法1的运行效率相对较高。属性个数是约简的基，约简集数是相同的基下的约简个数。对于Wine数据集（表5），共有78个约简，其中，当约简的基等于2时有47个约简，例如{a1,a2}，{a3,a9}。当约简的基等于3时有31个约简，例如{a4,a5,a12}，{a5,a6,a12}。

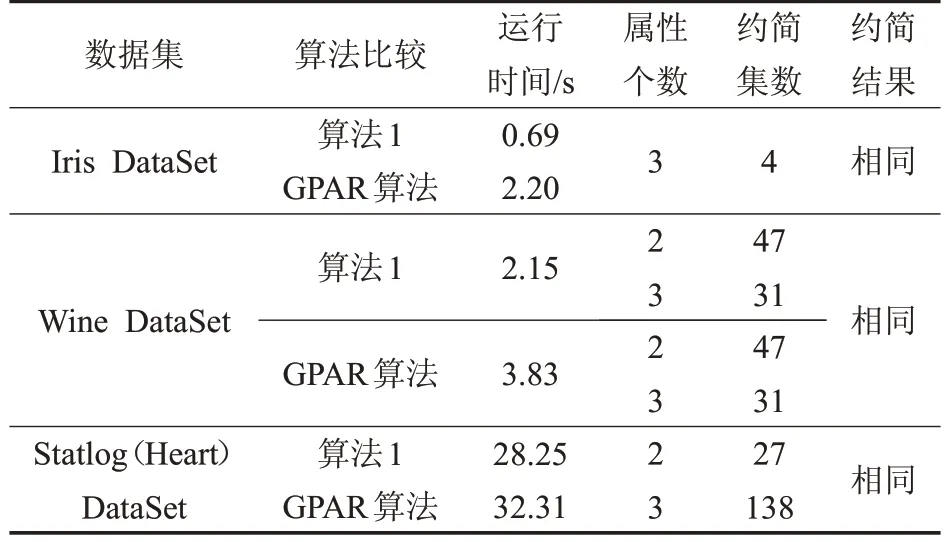
表5 算法约简结果对比

在选取3个数据集上，根据算法2得到带权决策表的近似分类精度约简结果如表6所示，其中，πD是决策属性集在论域上确定的商集U/D的子集。在Iris数据集中，D1为属性值为“Setosa”确定的等价类，D2为属性值为“Versicolour”确定的等价类；在Wine数据集中，D1为属性值为“1”确定的等价类，D2为属性值为“2”确定的等价类；在Statlog（Heart）数据集中，D1为属性值为“1”确定的等价类，D2为属性值为“2”确定的等价类。

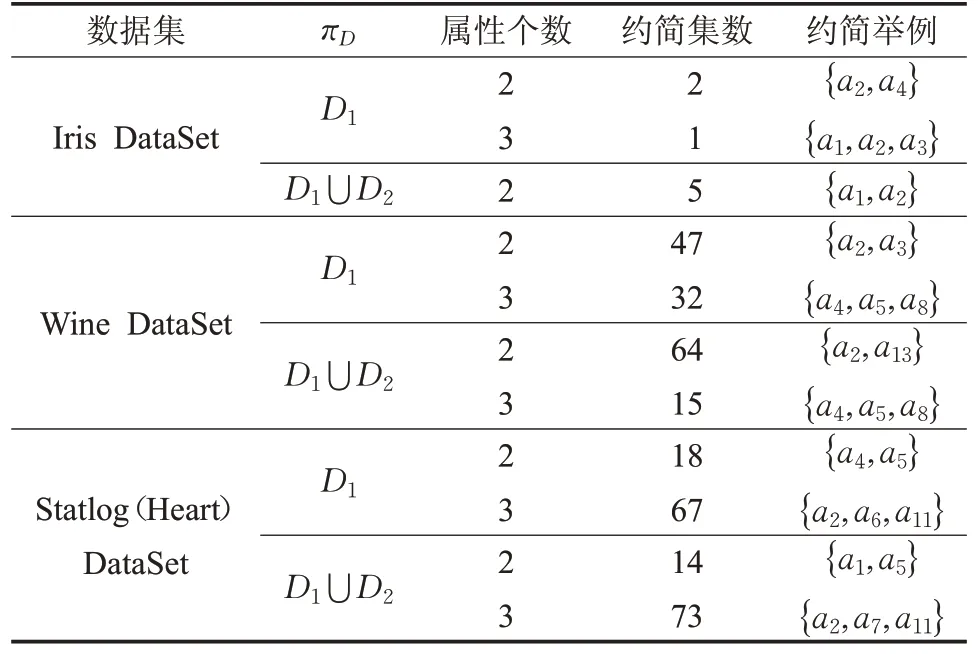
表6 近似分类精度约简结果

表6中，对于Iris数据集，取πD=D1时，有3个约简，其中当约简的基为3时，有1个约简{a1,a2,a3}，当约简的基为2时，有2个约简。取πD=D1⋃D2时，有5个约简，且5个约简的基均为2。通过实验进一步说明了本文提出的算法1和算法2具有可行性。

6 结束语

关于决策表中的约简研究取得了广泛的研究成果。在通常的决策表中，可通过GPAR算法得到正域的全部约简。本文将决策表转化为带权决策表后，通过算法1进行正域约简时发现，算法1的运行时间优于GPAR算法。同时，本文提出了一种关于近似分类精度约简算法，并给出了证明。最后通过实验说明本文提出算法的可行性和有效性。之后的工作中，通过带权决策表模型，来解决更多类型的约简问题，例如将等价关系推广至一般关系（即不要求关系满足自反性、对称性、传递性）。