DBD涡流发生器及其在角区流动控制中的数值研究

徐向南， 张华， 胡波

北京航空航天大学 航空科学与工程学院 教育部流体力学重点实验室， 北京　100083



DBD涡流发生器及其在角区流动控制中的数值研究

徐向南， 张华*， 胡波

北京航空航天大学 航空科学与工程学院 教育部流体力学重点实验室， 北京100083

为明确介质阻挡放电(DBD)涡流发生器对马蹄涡的影响，在采用唯象模型的基础上，通过数值方法研究了DBD涡流发生器诱导产生流向涡的结构特性及其对马蹄涡的控制特性。研究结果表明，流动在激励器上游边缘处形成羊角涡，自由剪切层卷入流向涡的涡核并为其提供持续涡量；在柱体根部角区流动中，当对称面两侧激励器诱导流动指向对称面，诱导涡与马蹄涡环绕方向相反时，马蹄涡可以得到有效抑制，反之，则控制效果不佳。最后得出，诱导涡对下游马蹄涡的控制机制体现在其黏性扩散作用、掺混作用以及低压效应3个方面。

DBD涡流发生器； 数值模拟； 流向涡； 角区流动； 马蹄涡

等离子体气动激励作为一种主动控制手段，具有响应快、频带宽、能耗低和无移动部件与复杂气体输运系统等优点；在提高升阻比[1-3]、增大失速迎角[4]、实现噪声控制[5-6]以及减弱激波强度[7]等方面具有广泛的应用前景，受到众多学者青睐[7-9]。关于等离子体流动控制机理存在两种观点：① 诱导周围气体流动，向边界层注入动量以抵抗更强逆压梯度；② 以激励器诱导涡结构来加强边界层内掺混作用，最终实现对附面层的有效控制。

以介质阻挡放电(DBD)等离子体激励器作为涡流发生器诱导产生流向涡可以作为一种新的设计理念，具有重要的研究价值。20世纪末，在Roth等[10]应用等离子体气动激励进行边界层流动控制的实验中，DBD激励器诱导产生流向涡的设计理念就已初见雏形。在数值模拟中，Riherd等[11]将蛇形电极条布置在翼型上，以诱导产生的完整空间涡结构实现了对边界层分离的有效控制，并且发现蛇形现象越明显，控制效果越好。随后，Riherd和Roy[12]指出流动在这种蛇形激励器控制下会表现出两种特性：① 在距离激励器很近的下游区域产生定向射流；② 诱导产生环绕方向相反的流向涡。Rizzetta和Visbal[13]应用大涡模拟对蛇形等离子体激励器作用下的低雷诺数翼型绕流进行了数值模拟，并分析了其作用机理。虽然该布置方式获得了和标准布置方式一样好的控制效果，加速了边界层流动，但不同之处是该布置方式产生的非均匀展向力抑制了二维涡结构的出现。以上有关蛇形激励器控制翼型分离的研究在一定程度上体现了DBD涡流发生器诱导产生流向涡的控制理念。

在双圆柱扰流实验中，Opaits等[4]引入了DBD涡流发生器的思想(即沿周向布置电极条)，有效抑制了上游柱体卡门涡街的脱落，进而促进了尾流与下游柱体的良性接触，实现了对噪声的有效控制。Okita等[14]在NACA翼型上沿流向布置电极条，并将DBD等离子体激励器作为一种涡流发生器，以其诱导产生的大尺度流向涡结构有效延缓了翼面分离。Schatzman和Thomas[15]在边坡流动控制实验中，以两对DBD涡流发生器诱导产生的一对环绕方向相反的流向涡实现了湍流边界层的再附；并且发现了相对于定常或非定常的展向布置理念，使流向布置方式在边界层掺混作用中体现出了更好的优越性。在此基础上，Jukes和Choi[16]通过实验对DBD涡流发生器进行了深入研究，发现流向涡的强度随着诱导速度与来流速度比率的增大而增大，且电极条与来流夹角为零时效果最佳。此外，在边坡分离控制实验中还发现，激励器诱导产生的一对反向涡比同向涡具有更好的应用前景。Jukes和Choi[17]指出，DBD涡流发生器诱导产生流向涡的机理可以从两方面考虑：① 横向壁面射流在来流边界层作用下被卷入流向涡中；② 来流边界层中的展向涡在激励器上游边缘处，受展向壁面射流的作用逐渐抬升扭曲卷入流向涡中，由二者共同作用形成集中流向涡。

虽然以上有关DBD涡流发生器的研究取得了一定成果，但诱导涡分离形态不清楚，且形成机理有待进一步分析；同时考虑到实验的局限性，DBD涡流发生器的一些细节特性容易被遗漏。基于此，本文应用Shyy等[18]提出的唯象模型，线性化处理作用区域内电场，将激励器激励对周围流场的势流[19]作用以体力形式添加到Navier-Stokes方程中求解；通过对DBD涡流发生器的数值模拟，探讨流向涡分离形态及形成机理，分析流向涡的发展过程以及在一定激励强度下来流速度、激励器长度、激励器与自由流夹角对流向涡的影响；并将其应用到角区流动中，研究其对下游马蹄涡的控制效果。

1　计算模型验证

本文应用Shyy等[18]提出的唯象模型，将激励器形成的电场限定在三角形区域内，并对其进行线性化处理，将等离子体对周围气体的影响作为激励频率、电压、电荷密度及等离子体形成时间的函数，以体力形式量化并添加到Navier-Stokes方程中求解。

为了验证本文提取模型的正确性，参照文献[18]中的设置进行二维数值模拟。将激励器布置在二维平板上，自由来流速度分别取为5 m/s 和0 m/s，基于壁面长度和自由来流速度的雷诺数为7 017，激励频率为3 kHz，均方根电压为4 kV，放电时间为67 μs，选用层流模型，详细布置参数如图1所示(二维计算域)，其中ST1、ST2、ST3和ST4为不同位置处的截面，其到壁面前缘距离分别为3.75、11、13.9 和17.3 mm。

图2为自由来流速度U0=5 m/s时，不同位置处的截面速度型，u为X方向的速度分量，很明显计算结果与文献[18]中的数据一致，自由来流在作用区域内被逐渐加速，在下游3.8 mm处达到最大值，从而验证了本文提取的等离子体数值模型的正确性。图3为静止空气中(即U0=0 m/s)，激励器诱导流动的速度矢量及X方向速度分量云图。假设以三角形体力作用区域为控制体，流体在控制体内受体力作用加速离开，由于质量连续守恒，控制体右上方气体被向下诱导，最终形成层流壁面射流[19]。从图3中可以发现，静止状态下激励器的最大诱导速度为W=11 m/s，距离壁面高度为δ=0.25 mm。

图1　二维计算域参数Fig.1　Parameters of 2D computational domain

图2　不同位置处的截面速度型Fig.2　Section velocity profiles at different positions

图3　静止空气中激励器诱导流动的速度矢量与X方向速度分量云图Fig.3　Flow velocity vector induced by actuator and contour of velocity component in X direction in quiescent air

2　研究模型

2.1DBD涡流发生器模型

将计算域扩展到三维空间以模拟DBD涡流发生器对周围流场的诱导作用，将长为L=30 mm 的激励器平行于来流布置，诱导产生横向壁面射流；其中自由来流速度U0=10、12、14、16 m/s，激励器前缘到壁面前缘距离为L1=50 mm，激励器下游根部到壁面前缘的距离为L2=80 mm，整个计算域在Z方向的长度为L3=170 mm，DBD涡流发生器模型如图4所示；该计算域网格数量约为400万，如图5所示。基于U0和L2的雷诺数为5.48×104～8.76×104之间，基于U0和L3的最大雷诺数为1.8×105，在Fluent中选用层流模型。随后改变激励器与自由来流的夹角α(以顺时针方向为正)，取α=-40°、0°、20°、40°、60°、90°，研究角度对流向涡的影响，具体结构如图6所示。

图4　介质阻挡放电(DBD)涡流发生器模型示意图Fig.4　Sketch diagram of dielectric barrier discharges (DBD) vortex generator model

图5　计算域网格Fig.5　Grids of computational domain

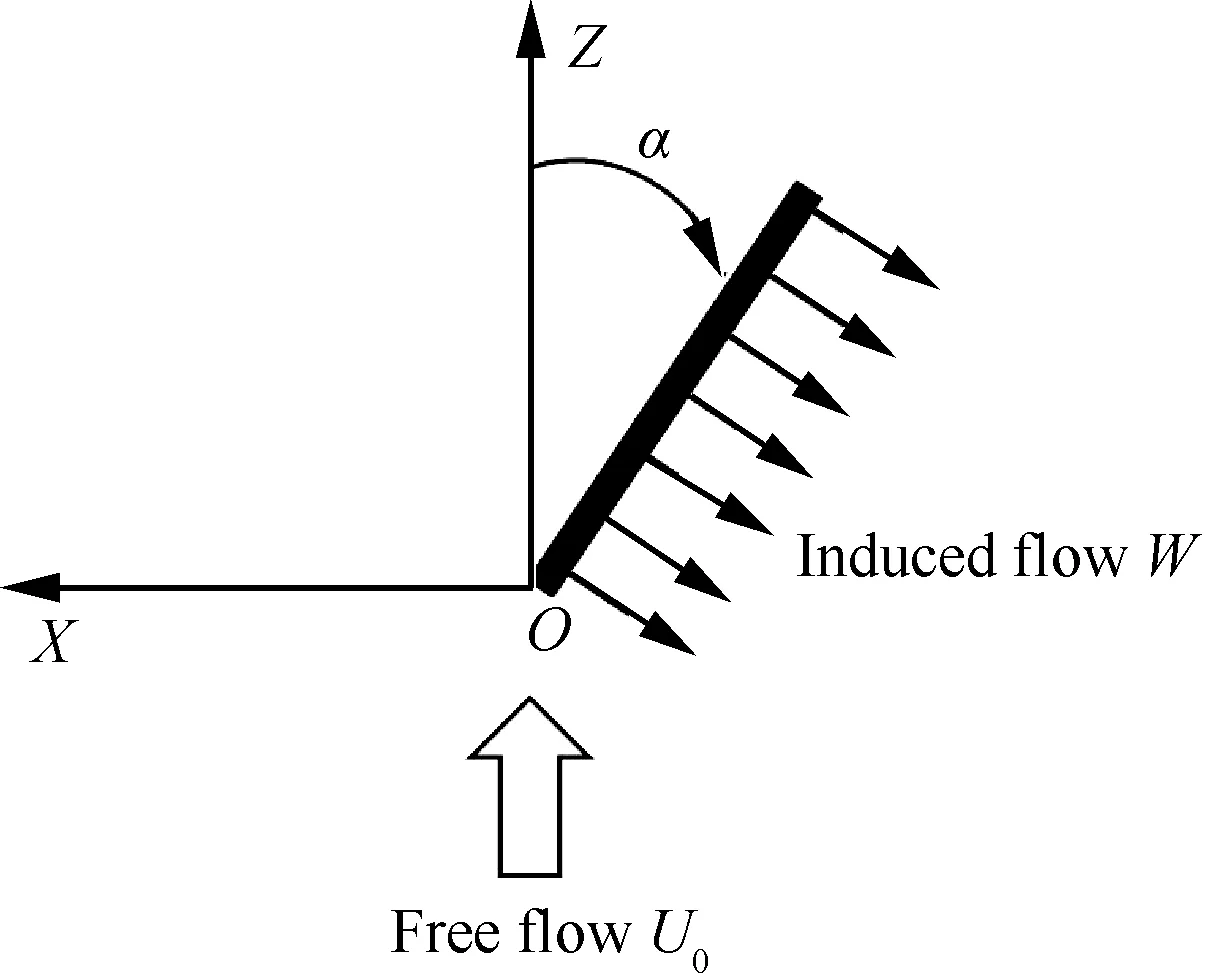
图6　激励器与自由来流的角度布置示意图Fig.6　Sketch diagram of actuator placed at a yaw angle to free flow

2.2引入DBD涡流发生器的角区结构模型

参照文献[20]，角区结构采用直径为D=100 mm、高为H=250 mm的柱体与平板组成，柱体前缘到壁面上游边缘的距离为L0=750 mm。柱体后缘到壁面下游边缘的距离为350 mm，自由来流速度为U0=10 m/s，基于U0和D的雷诺数为68 459。该状态下出现湍流分离，并伴随涡的随机性震荡[21]，湍流模型采用 S-A(Spalart-Allmaras)模型。将两对长为50 mm的激励器布置在对称面的两侧，与自由来流夹角α为 0°，激励外侧边缘到对称面的距离为J=0.05D，下游边缘到柱体前缘的距离为K=0.7D。依据激励器诱导流动方向，DBD涡流发生器的布置方式可以分为两种，即：诱导流动方向指向对称面(工况1)，如图7(a)所示；诱导流动方向背离对称面(工况2)，如图7(b)所示。

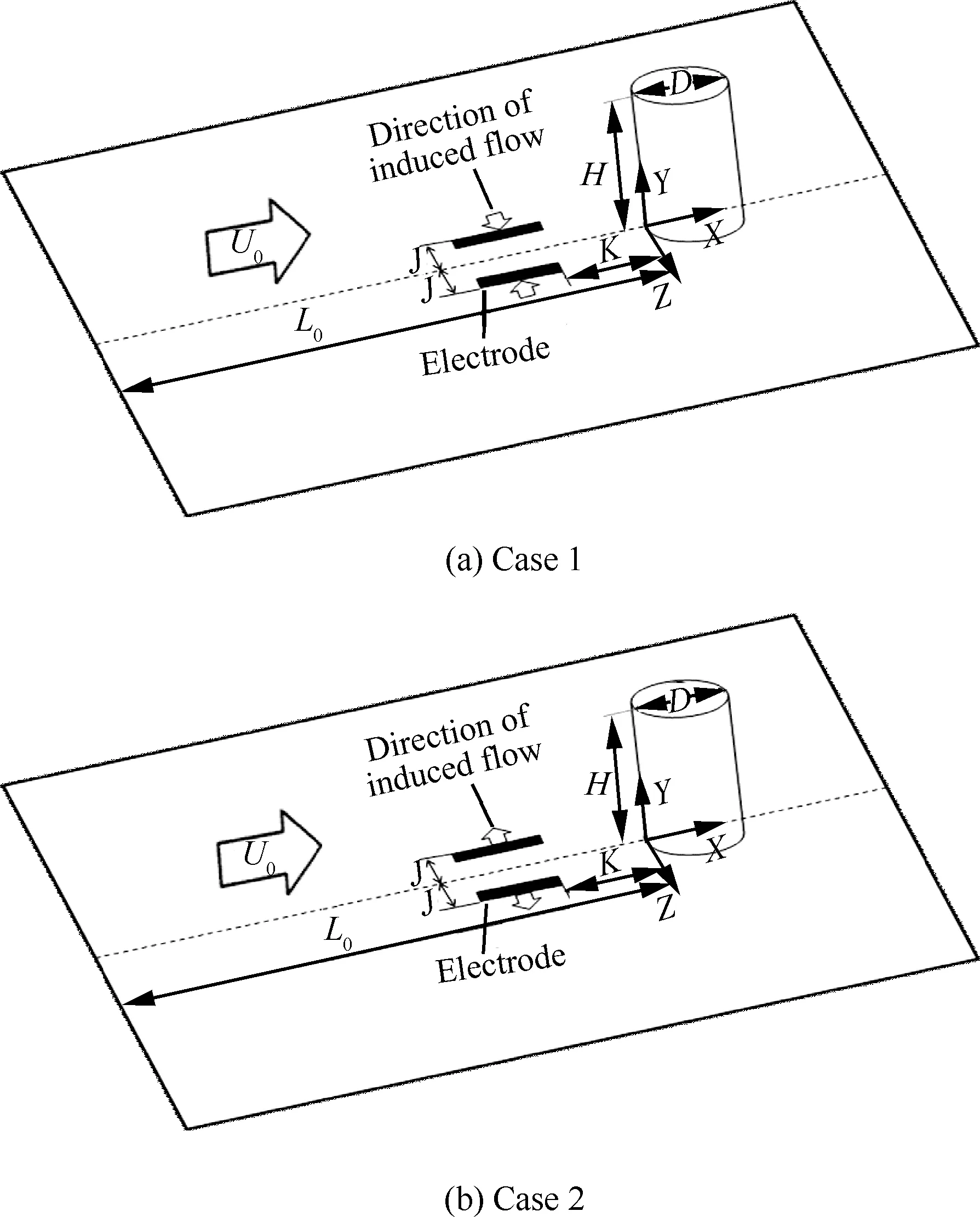
图7　引入激励器的角区结构示意图Fig.7　Sketch diagram of corner structure with actuator

3　DBD涡流发生器流场结构与特性

以U0=12 m/s和α=0°(即激励器与自由来流平行)为例讨论分离形式以及流向涡发展情况。流动在自由来流与壁面射流的作用下形成集中流向涡，结果如图8所示，其中图示涡核结构依据文献[22]中的Q法则提取，云图反映的则是基于激励器长度L和自由来流速度U0的无量纲化的Z方向涡量分布，其中ΩZ为Z方向的涡量大小。从图8中的空间流线环绕状态来看，流动在激励器上游边缘处分离，自由剪切层卷起构成流向涡的涡核；在激励器长度区域内的流动又产生持续分离，自由剪切层被卷入流向涡中。为进一步分析其分离形态，提取时均壁面摩擦力线，如图9所示。可以发现流动在激励器上游边缘处形成羊角涡，羊角涡在激励器作用下逐渐发展为空间流向涡，分离螺旋点N与右侧的鞍点S相连接形成典型的鞍点/螺旋点型分离[23]，以由鞍点S发出的三维分离线为起始的分离涡面围绕螺旋点N构成漩涡运动，为涡核发展提供持续涡量；而在激励器长度区域内，存在不从任何奇点发出的摩擦力线M，因壁面摩擦力线的方向与极限流线处处相同，可将其视为极限流线，则M可以作为三维分离线，构成开式分离。

图8　流向涡涡核结构及截面无量纲化涡量云图Fig.8　Streamwise vortex structure and contour of normalized vorticity on cross plane

图9　时均壁面摩擦力线Fig.9　Time-average wall friction streamlines

基本状态下，提取Z=5、10、20、30、40、50 mm 处XY截面内的时均速度矢量及无量纲涡量图，如图10所示。从图中可以看到，激励器附近的流体由于受到体力作用获得X方向的加速度而逐渐向侧向流动；考虑到质量守恒，体力作用区外的气被吸入控制体内，此过程为流向涡的形成提供初始环量[16]。在向下游发展过程中，流向涡始终在壁面射流的上方，涡心在向侧向以接近匀速运动的同时逐渐沿Y轴正向运动，而下方的壁面射流受流向涡的影响逐渐从壁面抬升。同时从图10中的涡量分布可以判断，在激励器长度区域内壁面，射流一直在向流向涡进行涡量输运，在激励器下游20 mm处壁面射流作用基本消失。

提取Z=5、10、20、30、40、45、50、60、70 mm处的XY截面，利用文献[20]中的复数特征值速度梯度张量法则来判断涡核的位置，即将涡核限定在某个速度梯度张量特征值为复数的区域，然后提取涡核边界S，并利用式(1)进行环量计算，得到不同自由来流速度下基于W和δ的无量纲化结果，如图11所示。

Γ=∮SudX+vdY

(1)

式中：Γ为环量大小；v为流动在Y方向的速度分量。

从图11中可以看出，在Z/L≤1范围内，当自由来流速度一定时，流向涡环量随着距离增长持续增加，与文献[16]中的结论一致；不同的是在Z/L>1以后的一段距离内，环量仍有一定程度的增加，并在激励器下游某处达到最大值，如U0=12 m/s时，流向环量在Z=40 mm处达到最大值。从图10(e)中Z=40 mm处的速度矢量及涡量分布可以发现，在流向涡的下方仍然有一定程度的壁面射流存在，这是因为受自由来流的影响，壁面射流在向侧向发展的同时有向下游扩展的趋势，因此它不是在电极条下游根部马上消失，而是存在消亡滞后现象。考虑到本文中激励器诱导速度与自由来流速度的绝对值相对于文献[16]较大，因此滞后现象相对较为明显，容易被捕捉。同时从图11中还可以看出，随着自由来流速度的增加，各截面涡核的无量纲环量逐渐减小；同时还发现相应的涡核内的涡量最大值并没有减小，反而逐渐增大，与涡核环量呈现相反的变化趋势。分析其原因，可能由于自由来流速度增加，流向涡被拉伸程度加剧，使得相应涡核截面面积逐渐被压缩，以致涡量变得较为集中，进而出现较大的截面涡量最值。随着来流速度增加，涡量耗散加剧，致使涡通量减小，涡强减弱，流向涡影响范围变小。

图10　XY截面内的时均速度矢量及无量纲化涡量云图Fig.10　Time-average velocity vector and contour of normalized time-average vorticity on XY plane

图11　不同自由来流速度下无量纲涡环量沿Z轴变化情况Fig.11　Normalized vortex circulation along Z axis for different free stream velocities

改变激励器与自由来流的夹角，沿来流方向截取Z=2L处的XY截面，同样应用具有复数特征值的速度梯度张量来提取涡核边界并进行环量计算，之后通过自由来流速度U0=12 m/s 与电极长度L对其进行无量纲化处理，得到如图12所示的影响结果。显然，随着角度的增加，流向涡环量变大，在α=0°(即电极条与来流平行)时取得最大值，但角度继续增加时环量又随即减小，结论与文献[16]中的实验结果一致。

图12　角度对流向涡环量的影响Fig.12　Effect of angles on streamwise vortex circulation

4　圆柱根部角区流动控制

4.1湍流模型验证

为了验证湍流模型的正确性，首先参照文献[20]，对自由来流速度为25 m/s、未施加控制状态下的流场进行数值模拟。图13为该状态下通过数值计算得到的时均壁面摩擦力线与文献[20]中的油流实验数据的对比，图中R为测量点离开柱体中心的距离。可以发现，由数值计算得到的分离线A和二次分离线B与文献[20]中的结果基本一致。

考虑到现有阶段DBD等离子体激励器诱导速度较低，为保证激励器可以诱导产生一定强度的流向涡，引入激励器后的自由来流速度为U0=10 m/s。图14为未施加控制时对称面内的时均流线图，其中，由数值计算得到主涡涡心到柱体中心线的距离为λ0=0.75D，主涡涡心到壁面的距离为ζv=0.04D，在0.028～0.073范围内，与文献[24]中的统计结果一致。综上所述，本节应用S-A模型得到的时均结果具有一定的参考价值。

图13　时均数值计算结果与实验数据[20]对比Fig.13　Comparison between time-average calculation results and experimental data[20]

图14　未施加控制时对称面内的时均流线图Fig.14　Diagram of time-average streamlines on symmetry plane in uncontrolled condition

4.2结果讨论

柱体上游对称面两侧布置激励器对可以诱导产生流向涡，其中自由来流速度为U0=10 m/s。截取X=-0.7D处YZ面的诱导涡示意图，得到结果如图15所示。工况1下，激励器诱导流动指向对称面，诱导涡如图15(a)所示，该涡结构与下游马蹄涡环绕方向相反；工况2下，诱导流动背离对称面，诱导涡如15(b)所示，该涡结构与下马蹄涡环绕方向相同。

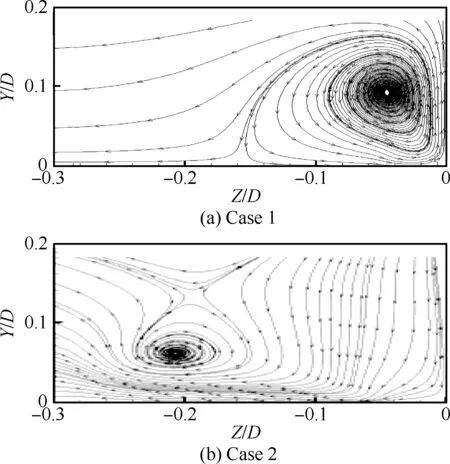
图15　X=-0.7D处YZ面内的诱导涡示意图Fig.15　Sketch diagram of induced vortex on YZ plane when X=-0.7D

图16为对称面上无量纲时均涡量及三维涡结构示意图。从涡量变化分析，相对于未施加控制时，工况1下的对称面上边界层内的涡量输运在激励器上游边缘处被阻断，激励器产生的涡结构改变了对称面上的涡量分布，使得马蹄涡内涡量极值的大小明显降低，且相应位置向柱体和壁面压缩。而相对于未施加控制状态，工况2下的对称面上涡量输运方式没有显著变化，且马蹄涡截面涡量极值大小相对增加，同时相应位置也向柱面产生一定程度的靠近。提取对称面上涡核边界进行环量计算，得到未施加控制状态、工况1以及工况2状态下基于自由来流速度U0与柱体直径D的无量纲环量分别为0.226 1、0.127 5和0.139 8，可以发现，施加控制后马蹄涡在对称面内环量显著降低。结合图16中的三维涡结构来看，工况1下激励器诱发的流向涡结构与下游马蹄涡环绕方向相反，这种与马蹄涡环绕方向相反的流向涡结构延伸到下游时，通过黏性的扩散作用大大降低了马蹄涡涡量的强度；从图16中可以看出，在对称面附近的马蹄涡空间尺度明显减小，且向下游延伸很短距离后消失。工况2状态下，虽然在对称面附近马蹄涡的空间尺度有所减小，但在向下游发展过程中，由于诱导涡与马蹄涡环绕方向相同，诱导与马蹄涡耦合时，使得马蹄涡可以继续向下游延伸。综合对称面上涡量分布、环量计算以及三维涡结构变化分析，工况1下的诱导涡与马蹄涡环绕方向相反，控制效果较好。

图16　对称面上无量纲时均涡量及三维涡结构示意图Fig.16　Sketch diagram of normalized time-average vorticity and 3D vortex structure on symmetry plane

图17为对称面上时均流向速度分量Ux的云图。可以发现相对于未施加状态下，工况1下的近壁流向速度分量Ux值虽然在激励器长度区域内减小，但在下游由于激励器产生诱导涡的掺混作用，动量大的质点被卷入近壁区域，加剧了边界层内外的动量交换，使得Ux值增大；工况2下，无论是激励器长度区域还是激励器下游，近壁速度都得到一定程度提升。总体而言，近壁速度的提升一定程度上可以削弱分离强度，进而降低马蹄涡强度。

从图18中的时均壁面压强系数作进一步分析，工况1下，在激励器长度区域内压强系数显著增大，并且在-0.7D～-0.2D区域内的压强系数也有一定程度提升，同时可发现柱体根部压强明显降低，这是由于诱导涡延伸到对称面附近时，该诱导涡的低压效应造成的。而工况2下，激励器下游压强系数整体上增加，并且压强梯度增大，同时可以发现柱体根部压强增加。

综上所述，工况1下马蹄涡强度得到有效控制的机理是：① 激励器诱导的流向涡与马蹄涡环绕方向相反，诱导涡延伸到下游时，通过黏性的扩散作用大大降低了马蹄涡涡量的强度；② 诱导涡的掺混作用使近壁区域速度增加，进而削弱了分离强度；③ 由于诱导涡可以延伸到对称面附近，诱导涡的低压效应使得柱体根部压强降低，进而使分离区域内整体压强梯度降低。相比之下，虽然工况2中诱导涡的掺混作用可以增加近壁速度，削弱分离强度；但因诱导涡与马蹄涡环绕方向相同，当诱导涡延伸到下游时对马蹄涡集中涡量没有消耗作用；同时诱导涡无法延伸到对称面附近，对对称面附近柱体根部压强起不到降低作用，所以控制效果不佳。

5　结　论

1) 流动在激励器前缘形成羊角涡，构成鞍螺旋点分离，由鞍点发出的三维分离线为起始的分离面绕螺旋点做螺旋运动，为流向涡涡核提供持续涡量。

2) 当DBD涡流发生器诱导的流向涡与马蹄涡环绕方向相反时，流向涡的黏性扩散作用、掺混作用、低压效应使马蹄涡强度得到有效抑制。

[1]POST M L, CORKE T C. Separation control on high angle of attack airfoil using plasma actuators[J]. AIAA Journal, 2004, 42(11): 2177-2184.

[2]ZHANG P F, LIU A B, WANG J J. Aerodynamic modification of a NACA 0012 Airfoil by trailing-edge plasma gurney flap[J]. AIAA Journal, 2009, 47(10): 2467-2474.

[3]毛枚良, 江定武, 陈亮中, 等. 受DBD等离子体控制的低速流动数值模拟方法研究[J]. 空气动力学学报, 2011， 29(2): 129-134.

MAO M L, JIANG D W, CHEN L Z, et al. Study of numerical simulation method for low speed flow with DBD plasma[J]. Acta Aerodynamica Sinica, 2011, 29(2): 129-134 (in Chinese).

[4]OPAITS D F, ROUPASSOV D V, STARIKOVSKAIA S M, et al. Plasma control f boundary layer using low-temperature non-equilibrium plasma of gas discharge[J]. AIAA Journal, 2005, 43(6): 1-6.

[5]THOMAS F O, KOZLOV A, CORKE T C. Plasma actuators for cylinder flow control and noise reduction[J]. AIAA Journal, 2008, 46(8): 1921-1931.

[6]KOZLOV A V, THOMAS F O. Plasma flow control of cylinders in a tandem configuration[J]. AIAA Journal, 2011, 49(10): 2183-2193.

[7]吴云, 李应红. 等离子体流动控制研究进展与展望[J]. 航空学报, 2015, 36(2): 381-405.

WU Y, LI Y H. Progress and outlook of plasma flow control[J]. Acta Aeronautica et Astronautica, 2015, 36(2): 381-405 (in Chinese).

[8]聂万胜, 程钰锋, 车学科. 介质阻挡放电等离子体流动控制研究进展[J]. 力学进展, 2012, 42(6): 722-734.

NIE W S, CHENG Y F, CHE X K. A review on dielectric barrier discharge plasma flow control[J]. Advances in Mechanics, 2012, 42(6): 722-734 (in Chinese).

[9]李应红, 吴云. 等离子体流动控制技术研究进展[J]. 空军工程大学学报： 自然科学版, 2012, 13(3): 1-5.

LI Y H, WU Y. Progress of research on plasma flow control technology[J]. Journal of Air Force Engineering University: National Science Edition, 2012, 13(3): 1-5 (in Chinese).

[10]ROTH J R, SHERMAN D M, WILKINSON S P. Electrohydrodynamic flow control with a glow-discharge surface plasma[J]. AIAA Journal, 2000, 38(7): 1166-1172.

[11]RIHERD M, ROY S, VISBAL M. Numerical investigation of serpentine plasma actuators for paration control at low Reynolds number: AIAA-2011-3990[R]. Reston: AIAA, 2011.

[12]RIHERD M, ROY S. Serpentine geometry plasma actuators for flow control[J]. Journal of Applied Physics, 2013, 114(8): 083303-1-13.

[13]RIZZETTA D P, VISBAL M R. Numerical investigation of plasma-based control for low-Reynolds-number airfoil flows[J]. AIAA Journal, 2011, 49(2): 411-425.

[14]OKITA Y, JUKES T, CHOI K S, et al. Flow reattachment over an airfoil using surface plasma actuator: AIAA-2008-4203[R]. Reston: AIAA, 2008.

[15]SCHATZMAN D M, THOMAS F O. Turbulent boundary-layer separation control with single dielectric barrier discharge plasma actuators[J]. AIAA Journal, 2010, 48(8): 1620-1634.

[16]JUKES T N, CHOI K S. Dielectric-barrier-discharge vortex generators: Characterization and optimization for flow separation control[J]. Experiments in Fluids, 2012, 52(2): 329-345.

[17]JUKES T N, CHOI K S. On the formation of streamwise vortices by plasma vortex enerators[J]. Journal of Fluid Mechanics, 2013, 733: 370-393.

[18]SHYY W, JAYARAMAN B, ANDERSSON A. Modeling of glow discharge-induced fluid dynamics[J]. Journal of Applied Physics, 2002, 92(11): 6434-6443.

[19]张攀峰, 刘爱兵, 王晋军. 基于唯象模型的等离子激励诱导流场数值模拟[J]. 北京航空航天大学学报, 2010, 36(1): 52-56.

ZHANG P F, LIU A B, WANG J J. Numerical simulation on flow induced by plasma actuator based on phenomenological model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(1): 52-56 (in Chinese).

[20]吴星钢. 基于二维/三维沟槽的角区流动控制实验研究[D]. 北京: 北京航空航天大学， 2014: 23-49.

WU X G. Experimental study on junction flow control based on two & three dimensional cavity[D]. Beijing: Beihang University, 2014: 23-49 (in Chinese).

[21]WEI Q D, CHEN G, DU X D. An experimental study on the structure of juncture flows[J]. Journal of Visualization, 2001, 3(4): 341-348.

[22]JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285(4): 69-94.

[23]夏雪湔, 邓学蓥. 工程分离流动力学[M]. 北京：北京航空航天大学出版社， 1991: 13-50.

XIA X J, DENG X Y. Engineering separated flow dynamics[M]. Beijing： Beihang University Press, 1991: 13-50 (in Chinese).

[24]DEVENPORT W J, SIMPSON R L. Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction[J]. Journal of Fluid Mechanics, 1989, 210(1): 23-55.

徐向南男， 硕士。主要研究方向： 流动控制。

E-mail: huilieri@163.com

张华男， 博士， 教授， 硕士生导师。主要研究方向： 旋涡与分离流动， 流动控制， 风工程， 风沙两项流动。

Tel: 010-82339908

E-mail: Ltszhh@buaa.edu.cn

胡波男， 博士研究生。主要研究方向： 旋涡与分离流动， 流动控制。

E-mail: hubohubo666@163.com

Numerical study of DBD vortex generator and application in junction flow control

XU Xiangnan, ZHANG Hua*, HU Bo

Ministry-of-Education Key Laboratory of Fluid Mechanics, School of Aeronautic Science and Engineering，Beihang University, Beijing100083, China

In order to explore the effects of dielectric barrier discharges (DBD) vortex generator on the horseshoe vortex, the phenomenological model is applied in the paper to the numerical simulation. The characteristics of the streamwise vortex structure and its control on the horseshoe vortex are analyzed. The results indicate that the tornado-like vortex is formed at the edge of the upstream electrode, and streamwise vortex engulfs the free shear layer and gains continuous vortices. When the induced flows on the two sides of symmetry plane point to the symmetry and the direction of the induced vortex is opposite to the horseshoe vortex, the strength of horseshoe vortex can be suppressed effectively in junction flow at the root of the cylinder. Otherwise the control effect is poor. Three factors, the viscous diffusion of the induced vortex on horseshoe vortex, and the mixing and low pressure of the induced vortex, related to the control mechanism are pointed out.

DBD vortex generator; numerical simulation; streamwise vortex; junction flow; horseshoe vortex

2015-10-21； Revised： 2015-11-18； Accepted： 2016-01-05； Published online： 2016-01-1114:55

National Natural Science Foundation of China (11372027)

. Tel.： 010-82339908E-mail: Ltszhh@buaa.edu.cn

2015-10-21； 退修日期： 2015-11-18； 录用日期： 2016-01-05；

时间： 2016-01-1114:55

www.cnki.net/kcms/detail/11.1929.V.20160111.1455.002.html

国家自然科学基金 (11372027)

.Tel.： 010-82339908E-mail:Ltszhh@buaa.edu.cn

10.7527/S1000-6893.2016.0006

V211

A

1000-6893(2016)06-1743-10

引用格式： 徐向南， 张华， 胡波． DBD涡流发生器及其在角区流动控制中的数值研究[J]． 航空学报, 2016, 37(6): 1743-1752. XU X N, ZHANG H, HU B. Numerical study of DBD vortex generator and application in junction flow control[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1743-1752.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160111.1455.002.html