三角形问题中添加特殊辅助线的途径分析
2016-11-14常爱国福州市日升中学福建福州350000
常爱国(福州市日升中学,福建福州350000)
三角形问题中添加特殊辅助线的途径分析
常爱国
(福州市日升中学,福建福州350000)
三角形是初中数学教学的重要内容之一,对三角形问题中添加特殊辅助线的一些途径(相似三角形法、延长线段法、特殊角法)进行细致分析,可以为学生在证明与计算某些几何图形问题时提供正确的数学思维方法。
初中数学;三角形;辅助线;解题
平面几何作为初中数学教学内容的重点与难点,对培养学生思维能力与创新能力有重要作用。在新课程标准背景下,教师必须基于先进教学理念的指导下,结合几何知识点的教学特点以及学生的实际能力、学习需求,采用灵活多样的教学方法,引导学生满怀兴致的进行几何学习。在几何教学中,许多三角形问题需要添加特殊辅助线才能求解,对三角形问题中添加特殊辅助线的一些途径(相似三角形法、延长线段法、特殊角法)进行细致分析,可以为学生在证明与计算某些几何图形问题时提供正确的数学思维方法。
一、相似三角形法
例1.等腰三角形△ABC(如图1所示),顶角为20°,底边以及一腰长分别为b、a,则判断如下等式中可成立的是()。
A.a3+b3=3a2b;B.a3+b3=3ab;C.a3+b3=3ab2;D.a3+b3=3a2b2。
在求解该问题时,根据已知条件,AB段以及BC段长度均为a,BC段长度为b,且B= 20°。为判断所给出等式是否成立,可引导学生把握题目特点,通过引入辅助线的方式得到相似三角形,然后尝试借助于相似三角形性质建立三角形边之间的关系,最后得出正确答案。绘制辅助线AD段后形成两个相似三角形△ABC以及△ADC(如图2所示)。

图1
在辅助线绘制好后不难发现,两个相似三角形△ABC以及△ADC具有△ABC~△ADC的关系,则根据相似三角形对应关系可以作出如下推断:
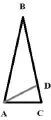
图2
DC/AC=AC/BC→DC=AC2/BC=b2/a;同时,∵BA=BC,且∠B=20°,∴∠BAC=80°,∠BAD=∠BAC-∠CAD=80°-20°=60°。
而在△ADB中,BD2=a2+b2-2abcos∠BAD,故可转换为(a-b2/a)2=a2+b2-2abcos∠BAD,经简化处理后可得到等式为a2+b2=3a2b。故选项A为正确答案。
分析认为:本题求解过程中通过添加辅助线的方式可构建与已知三角形相类似三角形,然后利用相似三角形的性质建立边与边之间的关系。通过绘制辅助线的方式,能够使解题思路更加清晰与简明,同时还引入了有关相似三角形判定以及性质的知识点,使学生在解题过程中能够加深知识之间的联系,简化解题步骤,提高解题效率。
二、延长线段法
在一些三角形特征比较模糊的题目中,通过常规的连接两点的方法难以理顺题目中的数量关系,学生往往难以把握解题的思路与方法,导致最终得出错误的结果。在遇到这些例题时,可以根据三角形相关题目的特点,选择延长线段的方法构建新的图形,以引出全新的数量关系,从而为学生对三角形相关问题的求解提供新的思路与途径。
例2.三角形△ABC中AD为已知中线(如图3所示),要求验证:AB+AC>2AD。
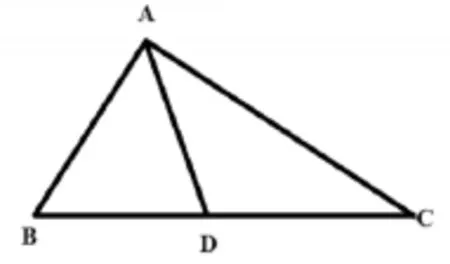
图3
学生通过对三角形相关知识点的学习,在教师引导下可以整理得到证明三角形边大小关系的思路,第一种思路是应用“两点之间线段最短”的基本原理;第二种思路是应用“三角形任意两边之和恒大于第三边”的基本原理。为给出验证三角形ABC中AB+AC>2AD规律,教师可引导学生做出推论,即如果将其归入一个三角形内,边的大小关系是显然的。因此,需要通过转移线段的方式加以证实。在对已知三角形进行进行延长时,通常所采取的是构建全等三角形的方案。
在添加辅助线时,可以将AD段延长至E点,令AD=DE,并将CE点连接。通过添加辅助线的方式可以构建起△ABC以及△ECD两个主要三角形(如图4所示)。在添加好辅助线后,对AB+AC>2AD的验证步骤可以总结为:
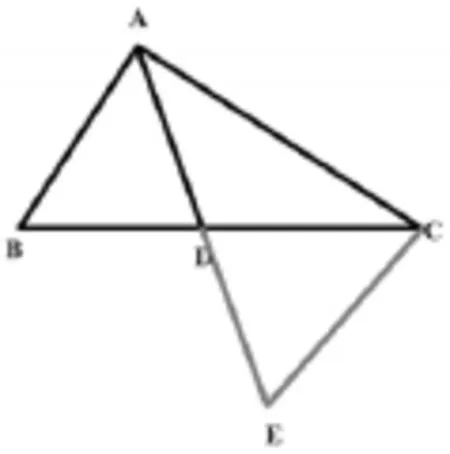
图4
在△ABC以及△ECD中,已知AD=DE,∠ADB=∠EDC;同时又有BD=CD,故△ABD≌△ECD,且有AB=CE。
在此基础之上,利用“三角形任意两边之和恒大于第三边”的基本原理,对于△ACE而言,有AC+CE>AE的恒定关系,故经过转换可得AC+AB>AE=2AD,进而可求证得到:AB+AC>2AD。
分析认为:在三角形中,任意两边之和恒大于第三边这一基本的原理是证明三角形各边大小关系的重要方法。当通过常规的连接两点或作出现的方法难以理顺题目中的数量关系时,可以根据题目已知条件中所给出的中线进行成倍延长,以构造全等边三角形,从而使解题思路更加顺畅,解题步骤更加简化。
三、特殊角法
在针对一些存在难度的三角形求解题目中,为进一步理顺学生的解题思路,可结合题目的实际特点以及所需要考察的内容,通过添加三角形辅助线的方式进一步挖掘题目已知条件中所蕴含的条件,使题目中各个条件之间不明显的关系得到充分展现。同时,添加辅助线还可以使条件得到合理转换,为学生的求解提供更加多样化的思路。
例3.已知某钝角三角形△ABC(如下图5所示)内角度数呈等差序列分布,且最大边边长与最小边边长比值为m,要求m取值范围为()。
A.m∈(1,2);B.m∈[2,+∞);C.m∈[3,+∞);D.m∈(3,+∞)。
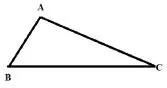
图5
结合图1已知钝角三角形△ABC,BC段边长>AC段边长>AB段边长,同时,可假定钝角三角形△ABC内BAC角度为a,ABC角度为b,ACB角度为c。同时已知条件中提示:“钝角三角形△ABC内角度数呈等差序列分布”,即可得到关系为a-b=b-c。由此可以计算得到b=60°。a取值范围则为90°<a<120°,c取值范围则为0°<c<30°。过该△ABC作角BAD使其与角b相等,均为60°(如下图6所示)。
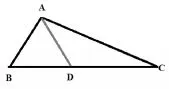
图6
根据图6则有c<30°∠CAD,故可以计算得到m>2,进而可选择得到正确答案。
分析认为:在对三角形问题的求解过程中,通过作辅助线的方式构成特殊角度,然后可根据题目所给出的已知关系与数据,确定角的大小关系。进而根据边角关系计算得到m的取值范围,给出正确答案。
四、结语
在平面几何教学中,三角形问题是教学的重点,学生掌握了三角形添加辅助线的方法与技巧,可灵活借助辅助线使用正确的思维方法解决许多问题。
[1]彭胜军.三角形全等证明题中常用辅助线的几种作法[J].初中生辅导,2012(16).
[2]来林芳.移动重叠构造全等——已知线段相等的一种辅助线添法探究[J].新课程(中旬),2015(2).
[3]吴建忠.例析不完整平行线型相似三角形中辅助线的添设[J].数理化学习,2012(5).
(责任编辑:王钦敏)
