换元法在高中数学中的“魔法”应用
2016-11-14江芳英武平县第二中学福建武平364300
江芳英(武平县第二中学,福建武平364300)
换元法在高中数学中的“魔法”应用
江芳英
(武平县第二中学,福建武平364300)
高中数学在教学中,以具体实例向学生介绍常见的整体换元、对称换元、数字换元、均值换元、三角换元等方法,促进学生使用换元法解决数学问题的思维水平。
整体换元;对称换元;数字换元;均值换元;三角换元
换元法是一种重要的数学方法,能够让复杂问题简单化,让生疏问题熟悉化。
解题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化的方法叫换元法。常见的换元法有整体换元、对称换元、数字换元、均值换元、三角替换等等。换元法在数学各分支具有广泛的应用,列举如下:
一、在求函数解析式中的应用
出现形如f[g(x)]=h(x)的问题中,常用整体换元。
二、在化简代数式中的应用
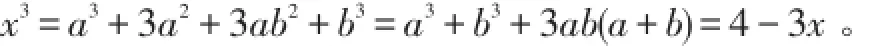
即x3+3x-4=0,
此方程的唯一实根是1,故化简结果为1。
三、在解方程中的应用
例3.解方程:x3+18x2+81x+8=0。
分析:这是三次方程,经仔细观察,若把9看成新的未知数,就可转化为一元二次方程了.令9=t,得
xt2+(2x2+1)t+x3-1=0,
接下来,把t用数字换回,就可进一步解出x了。
四、在求条件值域中的应用
例4.已知x2-y2=4,求的取值范围。
分析:利用三角替换,令x=2secθ,y=2tanθ(θ∈[0,
∴w∈(-6,10)。
常见三角替换有:已知a2+b2=1,令a=cosθ,b=sinθ,
已知|x|≤1,令x=cosθ,
已知|x|>1,令x=secθ,
已知x∈R,令x=tanθ。(注意各参变量角度的范围)
五、在三角函数中的应用
例5.求W=sin3θ+cos3θ+sinθcosθ+sinθ+cosθ的取值范围。
分析:考虑到sinθ+cosθ和sinθcosθ的关系,可令
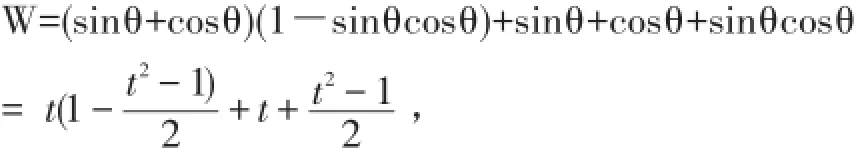
∴Wmin=f(-1)=-2。
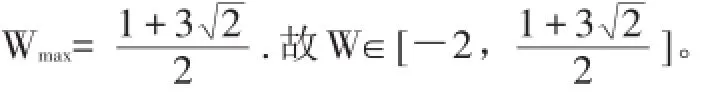
本例通过换元法,把比较复杂的三角函数问题转化为三次函数的值域,达到用导数解决问题的目的。
六、在数列中的应用
数列中的换元法,往往和构造新数列联系在一起,其意图大都是把一般数列转化成等差(比)数列。
例6.设b>0,数列{an}满足a1=b,
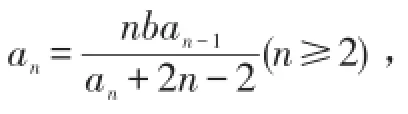
(1)求数列{an}的通项公式;
分析:①因为a1=b>0,由已知得:
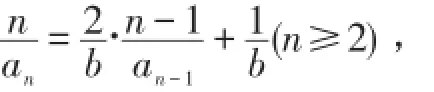
∴{bn}是一个首项为的等差数列,易得an=2,
∴{bn}是一个首项为的等比数列,
②根据(1)的结论,用分析法和综合法(均值不等式)易证,从略。
七、在不等式中的应用
在不等式的问题中,换元法也有很普遍的应用。如已知a+b=1,比较的大小,可作均值换元,
例7.正数a、b、c适合a2+b2+c2=1,求证:
设a3+b3+c3=A,由1=a2+b2+c2,得
即a3+b3+c3。
本题用换元法容易从个数和指数方面加以推广:
关于其它方面的问题,换元法还广泛应用于微积分中,如一些导数公式的推导,不定积分的求法等等。因篇幅所限,不再讨论。通过上面事例,可发现换元法有如下特征:①从书写的角度看,解题中用到换元法时,最后要还原成原来变量;②新、旧变量的取值范围及其关系,常是关注的焦点;③换元的一致性,即换元必须干净、彻底;④换元法绝不是简单的“无中生有”,它需要较强的观察力。只有具备了“大局观”,并能妥善处理整体与局部的关系,才能更好地使用换元法。
[1]卢正勇.数学解题思路[M].福州:福建教育出版社,1986.
[2]王钦敏.如何对数学教材进行有益的拓展与改造[J].数学通报,2013(1).
[3]龙岩市普通教育教学研究室.2015届高三数学总复习指导意见[Z].2014.
(责任编辑:王钦敏)
