快度在狭义相对论中的应用
2016-11-14李泽昊刘楚源
刘 娜 李泽昊 刘楚源
(中国人民大学附属中学,北京 100080)
快度在狭义相对论中的应用
刘 娜 李泽昊 刘楚源
(中国人民大学附属中学,北京 100080)
双曲函数不仅是一种数学表达形式,同时在粒子物理中也有非常广泛的应用.快度是双曲空间中一个虚构的角度,通过数学代换方法,可将狭义相对论中的速度变换公式表述成一个简单的双曲旋转,这一旋转角度就是快度.快度与速度变换中的β因子有关.本文详细推导了这一代换过程,给出快度与β因子的具体关系以及快度在能量和动量的表现形式.快度有非常丰富的物理意义,它不仅能把狭义相对论在双曲空间中表现为一种更加简单直观的形式,而且其本身蕴含粒子能量和动量的信息,在高能物理中也被科学家广泛应用.
快度;双曲函数;洛伦兹变换;粒子物理
1 狭义相对论和快度的发展
1905年,爱因斯坦在《论动体的电动力学》[1]一文中完整地提出了狭义相对论,这一理论改变了牛顿力学的时空观念,开创了物理学新纪元. 1908年,闵可夫斯基把时间坐标作为新的一维“空间”,同三维空间一起构成闵可夫斯基时空,在这种时空形式下,狭义相对论中的洛伦兹变换方程式得以进一步简化为双曲旋转[2],即在双曲空间中旋转一个虚构的角度.1910年,快度一词最早被科学家们使用[2].
下面我们将详细推导洛伦兹变换在双曲空间中的形式,并解释快度的意义.
2 洛伦兹变换在双曲空间的形式
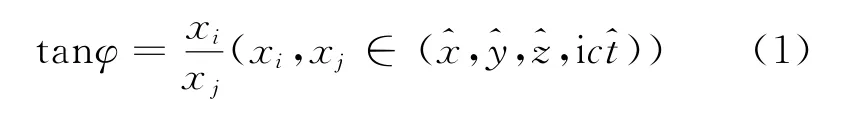
2.1 1+1维(1维空间和1维时间)的推导
发生在1+1维惯性系S中的事件可以用时空坐标表示为(x,i ct).

(x,i ct)事件,在相对S以速度v运动的惯性系S′中观测为(x′,i ct′).我们将v和所确定的平面定义为v-i ct平面.
这一洛伦兹变换为

由此,将R定义为双曲复空间中的一个旋转矩阵.可见,洛伦兹变换在该空间中可以表达为将坐标系绕垂直于v-i ct平面的轴旋转η角度,其中的η按式(4)定义,即快度.
2.2 2+1维(2维空间和1维时间)的推导
发生在2+1维惯性系S中的事件可以用时空坐标表示为(x,y,i ct).该事件在相对S以速度v运动的惯性系S′中观测为(x′,y′,i ct′).
首先,旋转S系得到S″(x″,y″,i ct″)系,使x″与速度v的方向一致,同时y″与速度v的方向垂直,这一旋转过程如下:


2.3 3+1维(3维空间和1维时间)的推导
对于发生在3+1维S系中的事件(x,y,z,i ct),在相对S以速度v(vx,vy,vz)运动的惯性系S′中观测为(x′,y′,z′,i ct′,),我们仍采用与2+1维相同的方法,先将S系进行两次旋转,第一次将x-y平面旋转到与v(vx,vy,vz)共面,旋转矩阵为M1,第二次将新的x轴旋转到与v共线的位置,旋转矩阵为M2.定义双曲旋转矩阵:M=M1M2变换后可以利用M-1得到S′系,于是在3+1维双曲时空中的洛伦兹变换仍为M-1RM.
以上证明了洛伦兹变换确实等效为在双曲空间中的角度旋转.
3 快度的物理意义
快度η不仅是双曲空间中一个虚构的角度,它在粒子物理中更广泛地被用来表示能量和纵向动量[3].
根据式(5):
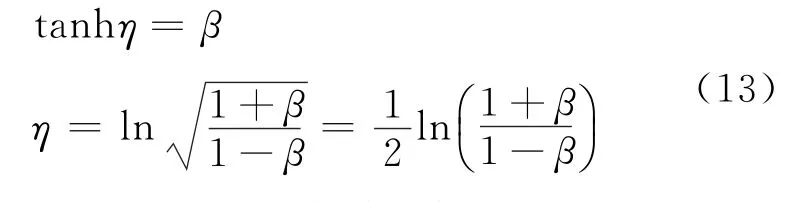
粒子的能量和纵向动量分别被定义为
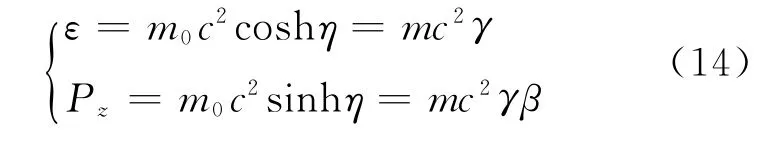
故沿着z轴以速度β运动粒子的快度为
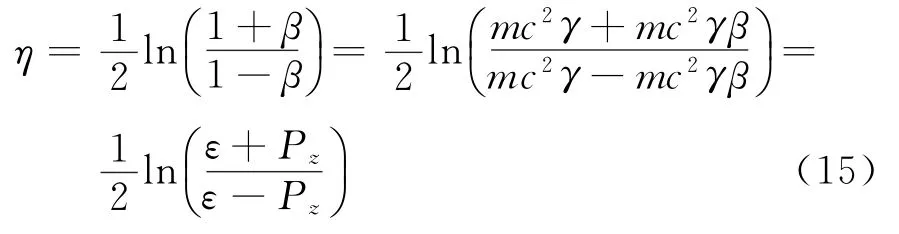
这便是粒子的快度定义[4]:

快度更普遍地用y表示,文中为了避免与坐标y混淆故用η表示.
4 结语
洛伦兹变换在双曲空间中可以被直观表述成坐标系的旋转,本文详细推导了这一过程.这一旋转的角度称为快度,它不仅与速度变换中的β因子有关,而且还蕴含了粒子能量和动量的信息,是粒子物理中常用的物理量.
感谢清华大学物理系阮东教授的讨论和指导.
[1]范岱年,赵中立,许良英.爱因斯坦文集(第2卷)[M].北京:商务印书馆,1977.
[2]https://en.wikipedia.org/wiki/Rapidity.
[3]石亚非,庄鹏飞,刘连寿.高能核-核碰撞的快度分布和多源模型[J].高能物理与核物理,1990(01):56-63.
[4]高能重离子碰撞导论[M].黄卓然,张卫宁,译.哈尔滨:哈尔滨工业大学出版社,2002.
APPLICATION OF RAPIDITY IN SPECIAL RELATIVITY
Liu Na Li Zehao Liu Chuyuan
(The high school affiliated to Ren Min University,Beijing 100080,China)
Hyperbolic function is not only a kind of mathematical expression but also widely used in Partical Physics.Rapidity is an imaginary angle in hyperbolic space,the Lorenz transformation in the special relativity can be seen as a brief hyperbolic rotation,and the rotation angle is rapidity,which is related toβin the Lorenz transformation.In this paper,we derived this substitution process,presented the relationship between rapidity andβ.The physical meaning of rapidity is very rich,it can not only express the special relativity into a simpler and more intuitive form in hyperbolic space,but also have wider and wider application in high energy physics due to the information of energy and momentum it contains.
rapidity;hyperbolic function;Lorenz transformation;partical physics
2016-01-12
刘娜,女,清华大学物理系博士,中学一级教师.liuna@rdfz.cn
刘娜,李泽昊,刘楚源.快度在狭义相对论中的应用[J].物理与工程,2016,26(4):55-57.
