线性规划模型在肠衣原材料分配中的应用
2016-11-14杜向然李春亚李旭娇
杜向然,李春亚,李 成,李旭娇
(天津海运职业学院,天津 300350)
线性规划模型在肠衣原材料分配中的应用
杜向然,李春亚,李成,李旭娇
(天津海运职业学院,天津300350)
天然肠衣被广泛地用于肉制品加工,肠衣企业都把提升肠衣生产效率和材料利用率作为企业发展的核心竞争力。利用冒泡思想来优化解决线性规划模型的算法,成功地解决天然肠衣的原材料分配问题。可以根据不同用户的实际要求,找到合适的原材料分配方案。
冒泡算法;数学建模;线性规划;肠衣加工
一、引言
近几年,国际市场和国内市场对于肠衣的需求在不断地扩大,肠衣企业间的竞争也变得更加激烈。传统的肠衣生产主要靠管理者和工人们的经验完成,这种方法的优点是速度快,缺点是占用过多的人力资源、加工速度慢,原材料的利用率低。肠衣企业为了提升企业自身的竞争力,几乎所有生产厂家都把提高产品生产率和原材料的利用率作为企业发展的核心任务。当肠衣原材料和成品规格是已知的情况下,如何按照公司的要求合理地设计出一套原料搭配方案,使得原材料的利用率最高,节约材料成本,这正是需要解决的问题。
用线性规划方法解决肠衣原材料的分配问题,并通过求解最优的目标函数找出材料的最佳分配方案。为了更加贴近企业提高原材料的利用率的需求,也就是使原材料剩余最少,加工后剩余的原材料需要降级使用,从而达到充分利用原材料的目的。求解线性规划模型时,一个新的求解方法被采用,该方法可以对解空间进行全局搜索,并通过冒泡算法的思想提高了程序的执行效率。本文中涉及的实验是在通过Java语言在Eclipse和JDK环境下实现的,它解决了matlab和Lingo只能在windows系统环境下解决线性规划问题的限制,而且操作简单。实验表明该方法可以在保证搜索准确性的前提下,有效地解决肠衣生产过程中的原材料分配问题。
二、线性规划模型求解
线性规划模型是运筹学的重要分支,它是辅助人们进行科学管理和规划的有效方法之一。线性规划研究的问题是如何在线性约束条件下使线性目标函数达到极值。1947年,乔治·丹齐格首次提出用单纯形方法来解决线性规划模型以来,经过60多年的发展,线性规划理论趋向成熟,它已经成功地应用到社会、经济、文化和工业等领域中。到目前为止,线性规划模型已经成为科学与工程领域广泛应用的数学模型,特别是在计算机能高速处理海量约束条件和设计变量的线性规划问题之后,线性规划就更加受到青睐。
(一)线性规划模型
线性规划问题的核心就是在满足线性约束条件的前提下,使线性目标函数达到最优(最大值或最小值)。线性约束条件可以用一组线性等式或线性不等式表达,目标函数用于衡量方案的优劣。根据线性规划的定义,线性规划问题即求取自变量x=[x1, x2, … xn]T的值,使得线性目标函数在线性约束条件下达到最大,线性规划问题的一般标准型为:
Maxf = c1x1+ c2x2+ … + c3x3
S.T.a11x1+ a12x2+ … +a1nxn<= b1
a21x1+ a22x2+ … +a2nxn<= b2
……
(1)
am1x1+ am2x2+ … +amnxn<= b1
xj>= 0 (j=1,2,…,n)
其中ci、aij、bi(i,j=1,2,…n)为给定的常数。
目标函数的确定是由自变量和达到目的之间的函数关系决定的,在实际应用中,自变量所受到的限制条件就是它本身的约束条件。当我们得到的数学模型的目标函数为线性函数,约束条件为线性等式或不等式时称此数学模型为线性规划模型。
(二)模型求解方法
求解线性规划模型的方法包括:单纯形法、大M法、两段法和图解法等,求解线性规划问题的相关软件包括matlab和lingo等。这些方法只能得到满足目标函数的一个最优解,而不能得到满足目标函数的多个解。为了解决避免这个问题,本文采用java语言中的for循环语句来实现从解空间中找到多个最优解。该方法通过快速地搜索每个变量的取值范围,全局搜索符合目标函数的所有解。图1描述了for循环的流程图。

图1 for循环流程图
如果只用for循环进行全局搜索,整个过程会产生很多重复搜索的地方,造成求解时间较长。为了提高解题的效率,避免不必要的时间浪费和减少程序的时间复杂度,冒泡算法被用于对循环程序进行优化,合理地减少程序的搜索空间。
冒泡算法的特点是每次都从未排序的记录中找出一个最大值(或最小值),使这个值以气泡方式逐渐往上“漂浮”,直至插入到排好序的记录中,已排好序的记录不需要做任何调整。这个特点可以被用于减少for循环的全局搜索范围。例如,在标准模型(1)中,每个变量之间是有约束关系的。例如式子a11x1+a12x2+…+a1nxn=bn,x1的取值范围是[0,bn/a11],当x1取定为某值时,x2的取值范围不是[0,bn/a12],而是[0, (bn/a11-x1)/a12]。相应的,x3,x4,…xn的取值范围也会发生相应的改变。冒泡算法优化循环语句的搜索范围可以避免重复搜索空间,减少求解线性规划模型所花费的时间。代码表示下。
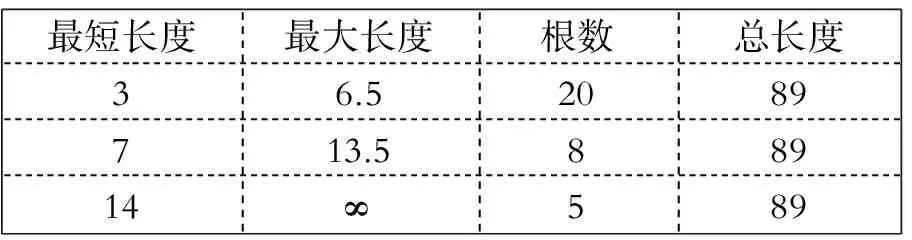
for ( int x1=0; a1x1 for (int x2=0; a2x2 …… for (int xn=0; anxn if (线性条件)// 同时满足的线性约束条件 { Maxvalue = c1x1+ x2x2+ …… + cn } } …… } } 所涉及的所有试验都是在一台笔记本电脑(Intel(R) Core(TM) i3 CPU M370 2.40GHz,3G内存,Windows XP系统)上实现的。具体的实现过程是在eclipse环境下用Java语言编写程序完成。实验中所使用的数据全部都来自于2011高教社杯全国大学生数学建模竞赛D题。已知材料中给出了肠衣的成品规格和原材料描述表,如表1和表2所示。 表1 成品规格表 表2 原料描述表 肠衣原材料需要按照指定根数和总长度组装出成品,也就是我们常说的捆。表1中给出了需要装出成品的几种规格,长度单位为米。符号∞在数学中表示无上限,但实际长度应小于26米。表2显示的肠衣加工原材料,这是由公司丈量好的。肠衣厂家希望设计一个原料搭配方案,使得装出的成品捆数越多越好。这里涉及到求最大值,我们可以根据线性规划模型求解。根据成品规格表描述的数据,成品被分为3种规格(3-6.5、7-13.5、14-26.)。0.5米被认为是每个档次的间隔米数,xi(i=1,2,3,…46)表示三种规格中每个档次实际产生的根数,yi(j=1,2,3)表示每个档次的最大捆数。如果出现成品捆数相同的方案,最短长度最长的方案被认为最好。考虑到实际生产过程中难免会出现误差,每种规格的总长度可以有±0.5米的误差,相应的总根数允许比标准少1根。目标函数是求解最大捆数,用y=y1+y2+y3表示,根据已知原材料,式子(2)、(3)、(4)三种规格的约束条件。 (2) (3) (4) 通过第二部分介绍的方法求解这个数学模型,我们得到了最优解的集合。第一种规格最多装出的成品捆数是11,成品的解空间为8(8种方案都可以装出最大成品捆数)。第二种规格最多装出的成品捆数是22,成品的解空间为3。第三种规格最多装出的成品捆数是42,解空间是31。在同一个规格中,对于成品捆数相同的方案,最短长度最长的方案被认为最好。根据这个原则,我们从方法集中找出{0 5 3 3 2 2 3 1 }作为第一种规格的最优解,因为在最短项里x1=0,而其他的x1都大于0。同道理,{0 1 0 1 0 0 0 0 1 1 1 2 0 1},{0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 0 0 0 0 0}分别是规格二和规格三的最优解。 为了提高材料的利用率,如果三种规格对应的原材料有剩余,相应的材料就可以降级使用。例如,对于长度为15米的原料可以降级到规格二中使用,制造出的成品属于规格二。 表3给出了降级后原料的剩余情况。 表3 降级后原料描述表 根据降级后的原料表和成品规格表,我们再次用上述方法建立并求解数学模型。三种规格的最优解分别是{7 1 1 1 1 0 2 6}、{0 0 0 1 1 1 1 0 0 0 1 1 0 2}、{0 0 1 0 0 1 0 0 0 0 2 0 1 0 0 0 0 0 0 0}。这时需要重复之前的方法,原材料再次被降级使用直到降到不能再降为止。通过总共9次(降级)迭代程序最终产生的最多捆数为:166捆。实验表明利用线性规划模型求解肠衣原材料分配问题是有效的,而且通过冒泡思想优化后的算法在运行时间上被大大缩短了,由之前的2931秒减少到1121秒(小于30分钟)。算法不仅可以满足用户的实际要求,而且有操作性较强、易于理解和实现等优点。 提出了一种肠衣原材料分配方案的数学模型,该数学模型首先从已给定的成品规格表入手,列出满足条件的线性方程,通过求解线性规划模型计算出每种规格中捆数最多的方法集(方法集中的每个方法都可以在相应的规格中组装出成品),然后从每种方法集中,根据用户的要求找出各自最好的方法。如果原料还有剩余的话,可是降级使用,提高产品的利用率。该模型的求解是通过改进后的循环程序对解空间进行全局搜索找出最优目标函数。为了使我们的模型更加贴近人的使用习惯,我们假设每次只取出一种方法作为该规格的最优方法,这样还保证了模型可以在一定的时间内(30分钟)产生最优方案。 [1]吴育华,杜纲.管理科学基础(第三版)[M].天津:天津大学出版社,2009. [2]李明.详解MATLAB在最优化计算中的应用[M].北京:电子工业出版社,2011. [3]李兴华.Java开发实战经典[M].北京:清华大学出版社,2009. [4]严蔚敏,吴伟民.数据结构(C语言版)[M].北京:清华大学出版社,2009. [5]黄雍检,陶冶,钱祖平.最优化方法——MATLAB应用[M].北京:人民邮电出版社,2010. [6]曹卫华,郭正.最优化技术方法及Matlab实现[M].北京:化学工业出版社,2014. [7]张峰,吕震宙,赵新攀.基于序列Shepard插值的结构可靠性分析[J].机械工业学报,2010,(05). Application of Liner Programming Model in Casing Raw Material Distribution DU Xiang-ran, LI Chun-ya, LI Cheng, LI Xu-jiao (Tianjin Maritime Vocational College, Tianjin, 300350) natural casings are widely used in the processing of meat products. The enterprises in the casing industry have promoted the production efficiency and material utilization ratio of the casing as the core competitiveness of the enterprise development. Optimizing the algorithm to solve the linear programming model with bubbling algorithm successfully solved the problem of raw material distribution of natural casings. A suitable raw material distribution program can be found according to the actual requirements of different users. bubbling algorithm; mathematical modeling; linear programming; casing processing 2015-08-15 杜向然(1982-),男,天津人,天津海运职业学院信息工程系助教,硕士研究生,主要从事人工智能与机器博弈,运筹学等专业的教学与研究工作。 O221 A 1673-582X(2016)11-0101-05三、肠衣原材料分配


四、总结
