利用干涉原理探索压强与空气折射率之间的关系

邓博文，梁小冲，于白茹，李 伟，李紫源，郝彦军，朱 俊，饶大庆，邹旭敏，穆万军

（四川大学 物理科学与技术学院，四川 成都 610064）

利用干涉原理探索压强与空气折射率之间的关系

邓博文，梁小冲，于白茹，李 伟，李紫源，郝彦军，朱 俊，饶大庆，邹旭敏，穆万军

（四川大学 物理科学与技术学院，四川 成都 610064）

在原有测量空气折射率与压强关系实验内容基础上，借助其他实验仪器中的光强检测仪测定一定采样比的光强，利用相位差法对条纹的移动数进行一定的修正。利用修正后的条纹移动数，拟合折射率与压强的经验公式。

折射率；压强；干涉条纹；经验公式

迈克尔逊干涉原理在测量微小位移的领域有着广泛的应用，用它可以观察光的各种干涉现象，测定单色光的波长、相干长度以及许多其他的物理量，如温度、压强、电场、磁场以及折射率等。目前在实验室中探索空气折射率与压强关系时，是在光学平台上搭建迈克尔逊干涉光路，在光路中加入压强可变的气室，当改变气室中的压强时，干涉条纹就会移动。通过观察条纹的移动数与压强的改变量就可以描述出压强与空气折射率的关系。实验时，将干涉条纹投影至功率计的光探头上，改变气室中的压强，功率计的数值就会发生变化。明暗相间的干涉条纹即对应着功率计的极大值与极小值。因为气室中的压强是通过一个放气阀或者橡胶压力球来调节，实验时很难控制压强的变化快慢，进而更不易准确地读出功率计的极大值与及小值。所以目前的实验仪器只能定性地进行观察折射率与压强的关系［1］。为了定量地得到折射率与压强之间的关系，引入其他实验仪器中的GSZF-3型光强检测仪，测定一定采样比的光强，并利用相位差法得到准确的条纹移动数。

1 实验原理

迈克尔逊干涉仪是以相干光源的干涉成像为基础的精确测量仪器。如图1所示，从激光光源发出的光（波长为633 nm）通过分束镜一分为二，光束1经过透射至M1反光镜上，再通过分束镜打在光屏上；光束1经过反射至M2反光镜上，再通过分束镜打在光屏上。两束光的光程差可以表示为:

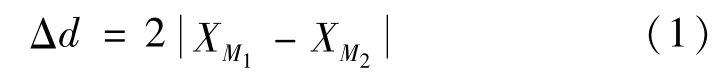
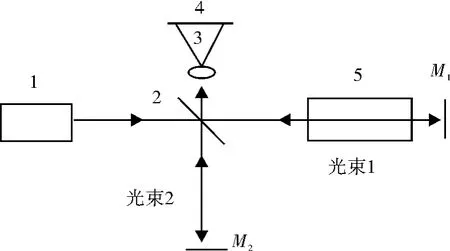
图1 迈克尔逊干涉仪

迈克尔逊干涉的相干条件是Δd小于等于波列长度，因此在实验中应使Δd尽量小，以使干涉现象明显。干涉现象产生后，仅半个波长的距离改变就会使干涉条纹产生肉眼可辨的变化，因为可见光的波长在10-7m数量级，因此迈克尔逊干涉仪的精确度能达到10-7m数量级［2］。

将气室5（长度为100 mm）放在图中分束镜2与反光镜M1之间，改变气室中的压强就会改变两束相干光的光程差，并且由于光路的特殊性，光程差的改变量是气室中压强带来光程差改变量的两倍。当压强不变时，两束干涉条纹存在不变的光程差；当压强改变，不考虑温度的影响时，气体折射率n与压强P有线性关系:

设压强从P0变化到P，折射率从n0变化到n，由式（2）可知:

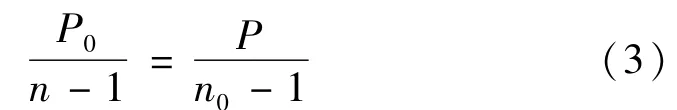
将长度为L的气室放在迈克尔逊干涉仪的一条光路中，压强从p0变化到p引起干涉条纹的变化数为m，则:

由式（3）与式（4）可知大气压强p相对应的空气折射率n的表达式为:

由式（5）可知，只要测出气室内压强由 P0变化到p时的条纹变化数m，即可由式（5）求出相应的空气折射率n0；实验中只要多次测出条纹的变化数Δm以及相应的压强变化Δp，将其取平均代入式（5），同样可计算出相应的空气折射率

2 实验方案与操作

搭好如图1所示的光路后，调整两反射镜的相对位置并向气室内打气加压。先用原实验仪器中的功率计来记录干涉条纹的移动数。

2.1 光功率计记录条纹的移动数

1）将干涉图样投射到一个可变光栏上，将光栏的光圈大小调至最小。

2）将光功率计中的光探头放在光栏后面，将光探头对准透过光栏的光束。光探头可以将光信号转变为电信号，光强的大小与转换成的电信号的电流大小成正比，因此可以通过光强计来观测光强的变化。

3）通过调整两个反射镜的角度和距离使干涉图样尽量变成粗细均匀的平行条纹。

4）将气室进行充气，当气室中的压强达到一个特定的数值时，在缓慢放气。

5）第一次不进行读数，在条纹缓慢变化的过程中读出光强值的最大值和最小值并进行记录。

6）在进行实验时，每到一次最大值便进行一次计数，直到条纹不再进行变化。

2.2 相位差法修正条纹的移动数

在前面实验的基础上，用偏振光实验中的GSZF-3型光强检测仪代替上一个实验中的光功率计，将光强检测仪通过转换器与电脑相连，并设置数据的采样率为50 Hz，这样就可以把采集到的光强信号经过数模转换后实时地传入到电脑，电脑再通过数据做出光强变化曲线图。我们需要得到的是峰值的数目，峰值时光强大小IMax以及光强的初值I1和末值I2。由光学知识知道:

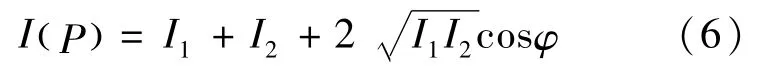
由于入射的两道光线光强近似相等，可得:

可由:

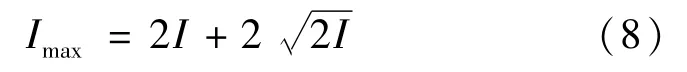
得出 I的值，再利用式（7）可以求出初光强I1对应的相位φ1和末光强I2对应的相位φ2。由于干涉条纹近似平行，因此可以通过算出初末条纹的精确条纹数差，进而提高条纹计数的精确度［6-7］。

3 实验结果与分析

本次实验在大气压强近似等于94.8 kPa的成都进行，实验结果如表1所示。

表1 光强计计数方法实验数据

实验数据处理如下:

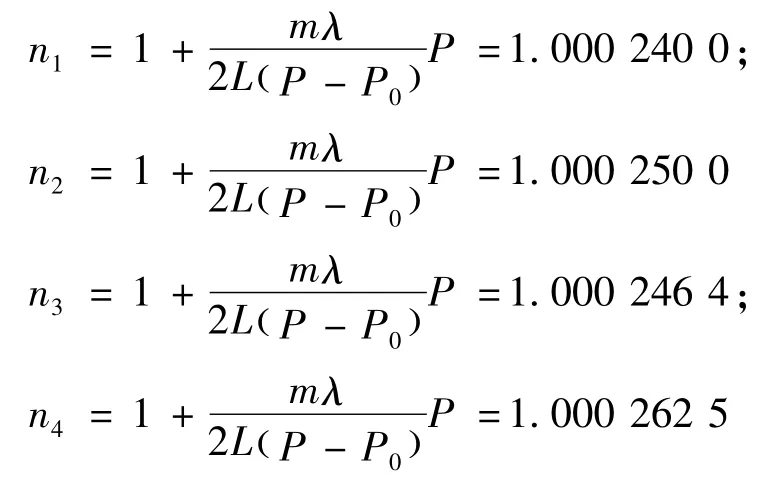
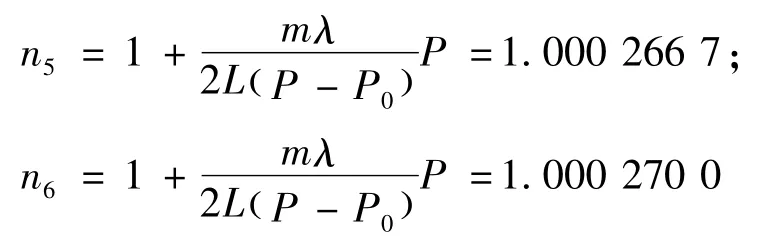
可得到条纹变化与压强之间的关系图像如图2所示，压强与折射率的关系如图3所示。

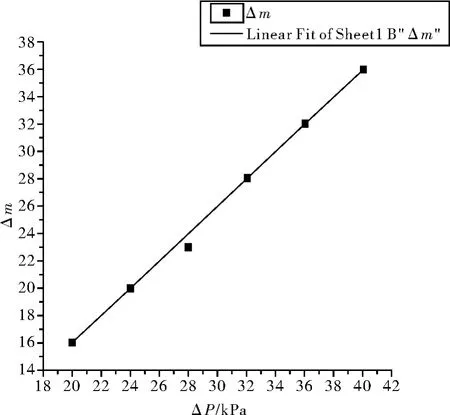
图2 干涉条纹与压强的关系

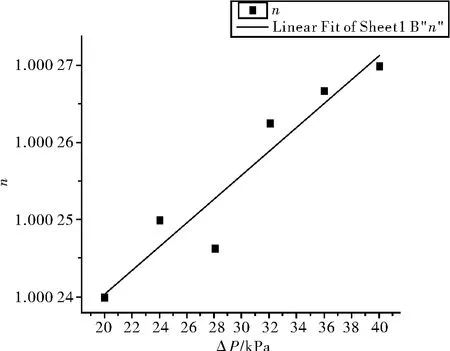
图3 折射率与压强的关系

可以看出除了第三个数据有较大偏差外，其他数据基本呈现正比状态。

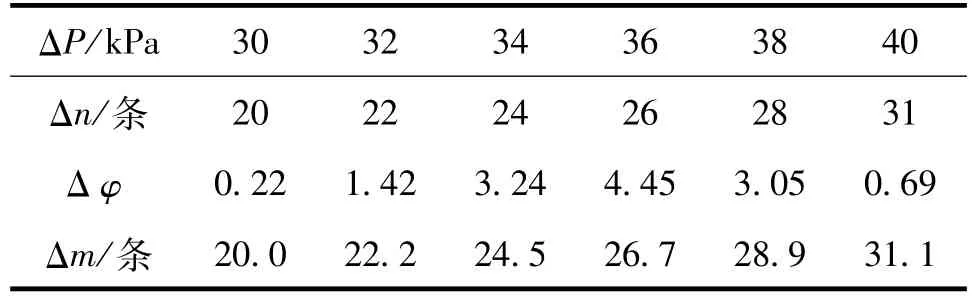
表2 相位差法记录的实验数据

表2中的Δn是光功率计测量得到的条纹数，Δφ是利用GSZF-3型光强检测仪得到的对应于在非峰值区域的相位差，采用式（7）和式（8）换算。最后一个Δm是光功率计测量得到粗略条纹数加上修正之后的最终条纹数。利用GSZF-3型光强检测仪得到的实验数据处理如下:

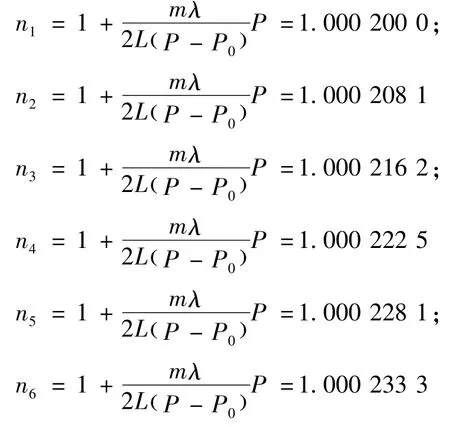
可得到条纹变化数与压强变化量的图像关系如图4所示，压强与折射率的关系如图5所示。

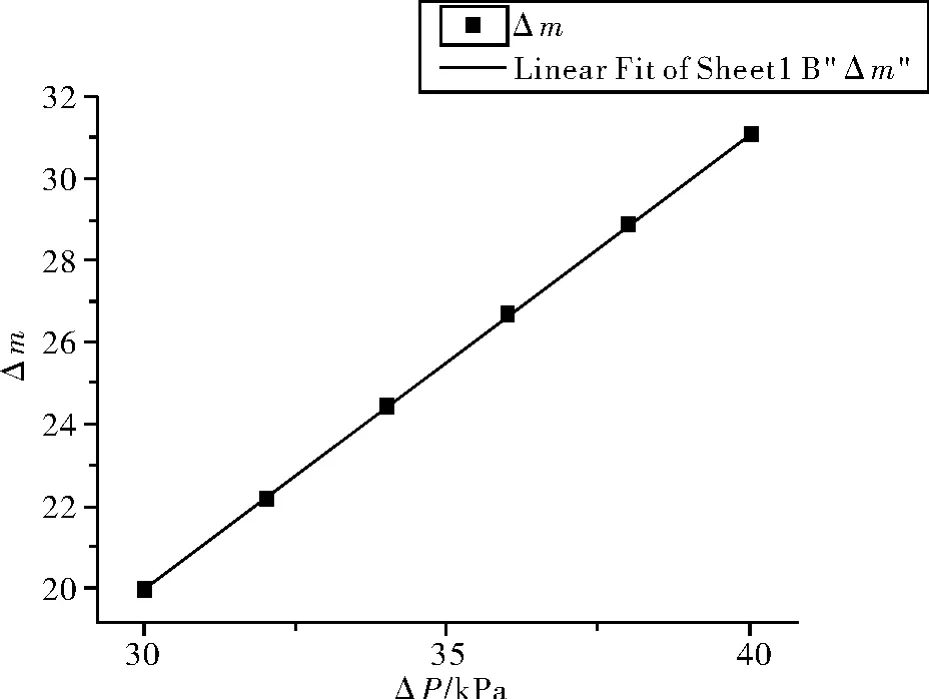
图4 干涉条纹与压强的关系

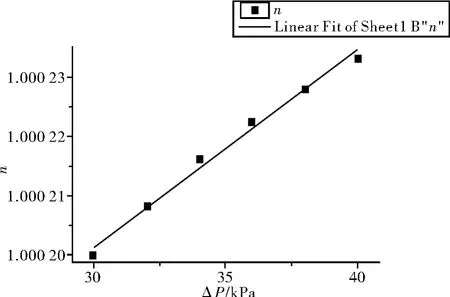
图5 折射率与压强的关系

可以观察出折射率与压强呈现明显的正比关系。由实验数据可以看出:压强值在相同的变化范围之内，利用GSZF-3型光强检测仪测量得到的条纹移动数目较多，这是因为当气室中的气压变化较快时，人眼无法及时地读出光功率计中的光强变化。

用人眼计数带来的误差可达到±0.5个条纹，对结果影响较大。原实验仪器的光功率计采样频率比较低，接收器的光阑选择过大或者过小都会对实验结果有较大的影响，而且很难记录下光强的变化。GSZF-3型光强检测仪采样频率的大小可调节，实验时把取样时间间隔取为0.02 s，根据光强的变化规律可知误差不大于光强变化最快时取样间隔带来的误差，经过计算可得误差范围内的Δφ为±0.01，对条纹变化数产生的误差为±1.59×10-3条。

根据表1和表2的实验数据，可以分别得到折射率随压强变化的经验公式:

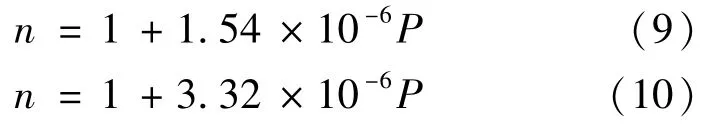
根据参考文献［3］得到的折射率与压强的关系:

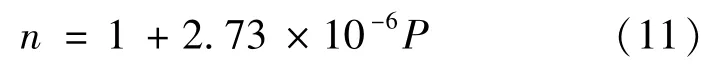
以［3］中的理论数据作为标准，式（9）的系数绝对误差达到了40；式（10）绝对误差为20，式（10）得到的结果更接近于参考文献［3］。两种方法得到的结果与参考文献［3］的差别都比较大，但是鉴于不同地区不同的空气密度、空气湿度、空气组成属于实验不可控因素，因此拟合的经验公式并不是普适公式，存在差异也在情理之中。

4 结束语

介绍了迈克逊干涉法探索空气折射率与压强之间关系的原理，利用自行组建的实验仪器并结合原实验仪器较准确地得到了空气折射率与压强之间的关系。在实验室现有条件下，学生自行组建实验装置，定量地测量出演示实验仪所展示的物理现象，有助于培养学生分析与解决问题的能力，激发学生对物理现象与物理规律探索的积极性。

［1］吕洪方，谭小平.迈克尔逊干涉微小尺度测量系统的研究［J］.江汉大学学报，2012，40（1）:40-43.

［2］王磊，陈钢，聂娅.大学物理学［M］.北京:高等教育出版社，2009，151.

［3］卢丹勇，刘长江，周惠君，周进.用M-Z干涉仪对空气折射率的定量测量与理论探讨［J］.物理实验，2012，26（12）:40-43.

［4］林江豪，马文华，漆建军，等.一种新的迈克尔逊干涉条纹计数方法［J］.微计算机信息，2010，26（1）: 141-142.

［5］敖天勇，向兵.新型迈克尔逊干涉条纹计数计的设计［J］.郑州大学学报，2008，29（1）:52-55.

［6］马科斯·玻恩，埃米尔·沃耳夫.光学原理［M］.北京:电子工业出版社，2005:76-82.

［7］MURPHY J C.AAMODT L C.Photothermal spectros-copy using optical beam probing:mirage effect［J］.J App1 Phys，1980（5l）: 4580-4588.

Relationship between the Refractive Index of Air and the Pressure Using the Principle of Interference

DENG Bowen，LIANG Xiaochong，YU Bairu，LI Wei，LI Ziyuan，HAO Yanjun，ZHU Jun，RAO Daqing，ZOU Xumin，MU Wanjun
（College of Physical Science and Engineering，Sichuan University，Chengdu 610064，China）

We modified the mobile stripes using phase correction based on the experiment content of the relationship between air refractive index and pressure，as well as with the help of other experimental instrument of light intensity detector.Finally，we fitted empirical formula of air refractive index and pressure using the revised stripe mobile number.

index of refraction；air pressure；interference fringe；empirical formula

O4-34

A

10.3969/j.issn.1672-4550.2016.05.014

2015-06-19；修改日期：2015-06-24

四川大学新世纪教改项目六期（SCUY044）。

邓博文（1995-），男，学士，高分子科学与工程专业。