周期个数设定对三线摆测量重力加速度的影响
2016-11-12俞莹
俞 莹
(东北林业大学 物理系,黑龙江 哈尔滨 150040)
周期个数设定对三线摆测量重力加速度的影响
俞 莹
(东北林业大学 物理系,黑龙江 哈尔滨 150040)
通过三线摆法测量三线摆下圆盘转动惯量原理,推导出利用三线摆法测量重力加速度表达式。为了提高三线摆法测量哈尔滨地区重力加速度的准确性,设定转动周期个数分别为5、10、20、30、40和50个。研究设定不同转动周期个数,空气阻力及悬线间摩擦对三线摆法所测重力加速度准确度的影响。发现设置测量周期个数为40个时,所测得的重力加速度最接近哈尔滨地区实际重力加速度值。
三线摆;转动周期;转动惯量;重力加速度
重力加速度是物理学中的一个重要参量。对其数值的准确测量对人们的日常生活、国防建设、科学研究都有着巨大的意义。在大学物理实验中常常利用单摆法、气垫导轨法来测量本地区的重力加速度[1-2]。三线摆法在大学物理实验教学中多数被采用测量刚体转动惯量[3-4]。利用三线摆测量刚体转动惯量的公式中含有参量重力加速度,因此可以设计利用三线摆测量本地区的重力加速度。
本文利用三线摆法通过转动惯量原理推导重力加速度表达式。针对周期测量对重力加速度的准确度产生的影响进行分析。在测量中采用多功能微秒计DHTC-1测量物体绕中心轴转动的周期大小。由于空气阻力及悬线间摩擦对转动时间的影响而导致对周期测量结果产生很大的影响。为了提高三线摆转动周期测量的准确性,下面利用改变周期测量个数的方法,分析周期对重力加速度值的影响。
1 理论推导和分析
1.1 重力加速度公式推导
图1为三线摆的扭转示意图。设上圆盘悬点至圆心O的距离为r,下圆盘悬点到圆心O′的距离为R,上下圆盘静止时的距离为H,悬线长为 L(悬线为不易拉伸的细线),下圆盘的质量为M,下圆盘绕OO′轴的转动惯量为I。下圆盘悬线间距离为b,上圆盘悬线间距离为a。在下盘扭动时,若某时刻其离开平衡位置的角度(角位移)为θ,当下盘离开平衡位置最远时,其中心升高h。

图1 三线摆的扭转示意图
根据简谐振动得到角位移方程:
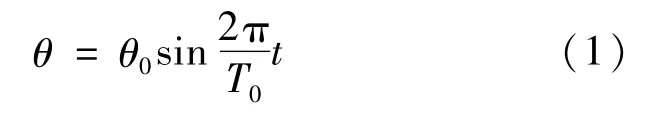
根据机械能守恒定律有:

即:

转动的角速度为:

将式(1)带入式(4)可得:

将式(6)带入式(3)得:

从图中的几何关系可以得到下列关系式:
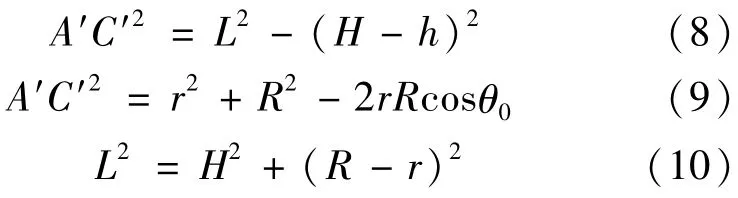
将式(10)带入式(8)得:

联立式(9)和式(11)可得:


下圆盘转动惯量(薄圆盘转轴通过中心与盘面垂直)的理论公式其中R′为下圆盘的半径,其值大于悬线到中心的距离R的值,d代表下圆盘直径。
利用比较法可得:
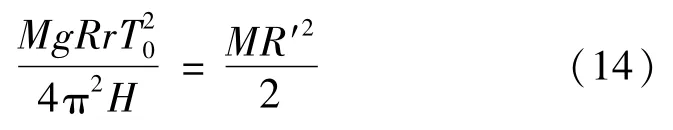
整理式(14)可得重力加速度:

2.2 实验数据及误差分析
如表1所示,为计算重力加速度时所需要的长度测量数据;表2为由图1中的几何关系计算得到的R,r,H,R′值;表3为转动时间的选择同周期大小的关系。

表1 长度测量结果数据表

表2 由图1中的几何关系得到的R,r,H,R′值

表3 周期次数的选择同周期大小的关系
由表1~表3得到不同周期个数下的重力加速度分别为g1=10.23 m/s2,g2=10.30 m/s2,g3= 10.17 m/s2,g4=10.18 m/s2,g5=9.83 m/s2和g6=10.19 m/s2。根据全国各地重力加速度表得到哈尔滨重力加速度为9.806 6 m/s2。在上述重力加速度中最接近哈尔滨实际重力加速度的为g5,其转动时间选择为40个测量周期的时间。
由实验结果发现,当测量少于40个周期时,所测得的重力加速度大于实际值。分析产生这种现象的原因是因为圆盘开始扭转时悬线由静到动,则使得悬线和圆盘小孔之间产生摩擦力,下圆盘的简谐振动不规律,需要经过一段时间才能使悬线自如转动。因此测量的周期数少则会因为很难克服悬线和圆盘小孔之间摩擦力的影响,而使得测量结果误差大;测量的周期数越多,摩擦力产生的影响就越小。然而当测量为50个周期时,所测得的重力加速度也大于实际值重力加速度。这是由于空气阻力对周期产生的影响也使得测量的周期小于实际值。测量的周期个数越多,受空气阻力影响越大,三线摆转动周期越小于实际值。
因此为了克服空气阻力和悬线摩擦力的影响,选择适合的转动周期个数,提高三线摆法测重力加速度的准确性。
2 结束语
设定适当的三线摆转动周期个数,有利于克服空气阻力和悬线与圆盘小孔间的摩擦力对三线摆转动惯量测量时所产生的影响。通过本文的分析,在哈尔滨地区利用三线摆测量下圆盘的转动惯量选择40个测量周期为最佳。
[1]苏润洲,兰城,崔金刚.大学物理实验[M].青岛:哈尔滨工程大学,2012,32-34.
[2]栾照辉,张颖,陆世杰,等.大学物理实验[M].北京:中国电力出版社,2014,48-50.
[3]温千宏,尹安东,孙俊,等.汽车复杂旋转部件转动惯量测试方法的研究[J].安徽工学院学报.1997,16(4):44-46.
[4]张代胜,胡玺良,袁玲.三线摆法测量复杂构件转动惯量的误差分析[J].农业机械学报.2008,39(3): 37-40.
[5]赵敏福.三线摆测量转动惯量的误差分析[J].科技信息,2009(2):408-409.
[6]夏雪琴.“比较测量法”在三线摆实验中的应用[J].大学物理实验.2011,24(5):48-50.
Influence of the Number of Cycles to the Gravity Acceleration Measured by Three Line Pendulum
YU Ying
(Department of Physics,Northeast Forestry University,Haerbin 150040,China)
The three wire pendulum method was used to deduce the rotary inertia of the three wire pendulum.Furthermore,the principle was used to deduce the expression of acceleration of gravity.In order to improve the accuracy of gravity acceleration in Harbin area by three wire pendulum method,the rotation period number is 5,10,20,40,30 and 50,respectively.The impact of the air resistance and friction between suspension lines to acceleration of gravity was analyzed by choosing different the number of rotation period.According to the compare between the Haerbin gravity acceleration of experiment and Haerbin gravity acceleration of reasonable,the optimal numbers of rotation period is 40.
three-line pendulum;rotation period;moment of inertia;gravity acceleration
O4
A
10.3969/j.issn.1672-4550.2016.05.007
2015-07-12;修改日期:2015-08-12
俞 莹(1981-),女,博士,讲师,主要从事光学方面的研究。
