强混响背景下LFM信号回波检测*

舒象兰，孙荣光，马 鑫

强混响背景下LFM信号回波检测*

舒象兰**，孙荣光，马 鑫

（海军潜艇学院，山东青岛266199）

混响是主动声纳检测的主要背景干扰，由于它是一种非平稳的有色噪声，使得工作在白噪声条件下的检测器性能受到极大限制。在混响背景下实现目标回波检测，常采用自回归（AR）模型对宽带回波预白化处理，但在强混响背景条件下，白化后直接进行匹配滤波检测的结果不甚理想。针对此问题，在AR模型预白化基础上，提出一种改进方法，对白化后信号先进行二分奇异值分解（SVD）处理，有效去除大部分混响干扰，然后再作匹配检测。仿真实验分析表明，相比于仅白化后的匹配滤波检测，该方法可提高信混比约3 dB，匹配检测效果得到了明显改善。

主动声纳；线性调频信号；回波检测；强混响；预白化；匹配滤波；信混比

1 引 言

在浅海区域中，对于主动声纳来说，除受到海洋环境噪声、舰船噪声等背景噪声的干扰外，还受到混响信号的干扰。混响是一种具有非平稳非高斯特性的有色信号[1-2]，由于其频谱结构与发射信号具有很强的相似性，所以带通滤波器无法达到滤除混响的目的。匹配滤波器是高斯白噪声背景下的最佳检测器，对混响进行预白化处理，可以实现次最佳的检测，但在强混响背景下，白化后的信混比仍然很低，这种处理的检测结果也不甚理想。

国内外学者对混响背景下的回波检测作了大量的研究工作。文献[3]提出了基于自回归（Auto-Regressive，AR）模型预白化处理的方法，在混响局部平稳的前提下将非高斯有色混响预白化处理，已成为混响背景下信号检测的主要方法[4]。文献[5]在AR模型的基础上，通过仿真和实验数据证明了白化处理后的次最佳检测器比未白化匹配滤波在检测性能上可提高3 dB。文献[6]进一步考虑到混响非高斯的特点，采用混合高斯模型，利用期望最大化（ExPectation Maximuzation，EM）等方法对非高斯混响进行参数估计，构造高斯化滤波器，使混响背景高斯化。文献[7]则利用了混响和回波在高阶统计量上的特征差异，研究了基于高阶累积量AR模型估计的回波检测，但是由于高阶累积量求取数据量大，不利于实时处理。文献[8-11]利用分数阶傅里叶变换进行滤波处理，达到了一定的混响抑制效果，但是这种方法适用性不强，只局限于线性调频（Linear FrequencY Modulation，LFM）信号，对其他宽带信号的检测性能不高。

为了提升强混响背景下的回波检测性能和效率，本文提出一种改进方法，先进行AR模型预白化处理，然后对白化后信号进行二分奇异值分解（Sin_ gular Value DecomPosition，SVD）处理，使得大部分混响干扰得到抑制，从而有利于改善匹配滤波器的检测性能，仿真分析验证了该方法对LFM信号回波检测的有效性。

2 AR模型混响预白化

混响是一种参数随时间变化的时变随机过程，可以将混响时间序列Wn表示为一个高斯白噪声序列Un激励一个线性系统的输出[12]：

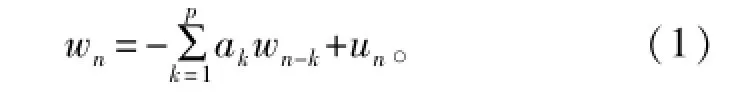
式中：αk是AR模型的系数；p为模型阶数。该模型就是混响的自回归（AR）模型。对于有色混响背景下的信号检测，不能直接使用白噪声条件下的匹配滤波器，最佳策略是先进行白化处理，然后再通过匹配滤波检测。如果已知上述AR模型的系数，便可以构造白化滤波器，其传输函数如下：

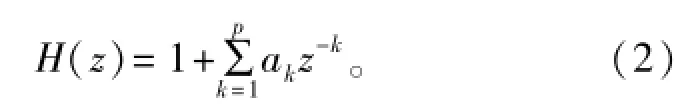
将混响数据Wn通过此白化滤波器，便可以得到预白化后的新数据：

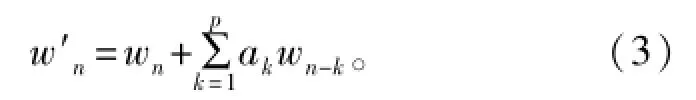
基于AR模型的预白化方法需要估计系数αk和模型阶数p。自相关法是AR模型参数估计的一种简单而又实用的方法[13]，即通过求解下述的Yule-Walker方程来估计模型参数：

其中，

只要估计出Wn的p＋1个自相关函数rWW（0），rWW（1），…，rWW（p），就可以求解方程。由于混响信号的非平稳随机特性，在包含回波信号的情况下，不可能估计出纯混响的功率谱密度来做最佳匹配检测。因此，假设混响具有局部平稳性，实现的是一种次最佳检测[14]。将接收数据分段进行“准平稳化”处理，即用前一段纯混响数据来近似当前时间的混响功率谱密度，并考虑1/2重叠，混响的局部平稳性可用相邻两段混响的功率谱的Itakura距离来衡量[15]，Itakura距离越小，说明信号越平稳，当Itakura距离小于0.3时，可近似认为此时间段内的混响是局部平稳的[16]。若数据x1（t）和x2（t）的功率谱分别为s1（ω）和s2（ω），非对称的Itakura距离为

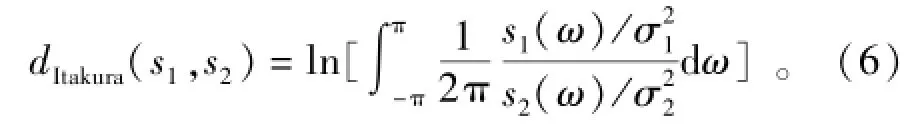
经AR模型预白化后，混响背景便具有类似白噪声的特性，与发射信号的相关性大大降低，从而可以使用匹配滤波器对目标回波进行次最佳检测，但在强混响背景下，预白化处理并不改变信混比条件，这也是造成匹配滤波器性能下降的最主要原因，因此，提升匹配滤波器性能最直接的办法是抑制混响、改善回波信混比条件。

3 二分SVD法抑制混响

2010年，赵学智[17]提出了一种多分辨SVD包理论，基于奇异值分解理论将信号和噪声按奇异值大小逐层分为低频和高频两部分，其分离的本质是基于正常信号和噪声的相关性不同[18]，在信号消噪方面具有比小波分解更多的优越性。关于目标回波与混响相关性的研究已经表明，将目标回波从不相关的混响背景中盲分离是可行的[19]，这也为本文引入多分辨SVD包理论对预白化后的信号进行混响抑制提供了理论依据。

二分SVD是奇异值分解的一种特殊形式。根据SVD分解理论：对于任意矩阵A∈Rm×n，总是存在正交矩阵U＝（U1，U2，…，Um）和V＝（υ1，υ2，…，υn），其中U、V∈Rm×m，使得下式成立：

式中：S＝（diag（σ1，σ2，…，σq），O），S∈Rm×n，q＝min（m，n），σ1≥σ2≥…≥σq≥0，σi称为矩阵A的奇异值。二分SVD方法就是将信号X＝（x1，x2，…，xN）分段重新排列，构造行数为2的如下矩阵：

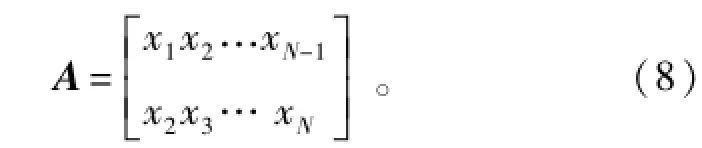
该矩阵经过SVD处理后，只能得到两个奇异值，信号被分解为以低频成分占主导的近似分量和高频成分占主导的细节分量，将各信号分量分别继续分层分解，则可以达到多分辨的目的，类似于多层小波分解。假设对噪声中的信号进行1层二分SVD处理，那么，可以得到两个子信号的矩阵空间：

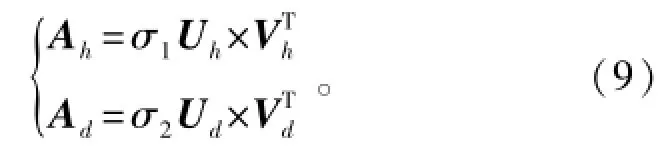
式中：Uh和分别是低频近似分量的左右奇异向量；Ud和VTd分别是高频细节分量的左右奇异向量。在强混响背景条件下，将预白化后信号进行二分SVD分解，混合信号矩阵按能量大小被自动分解为信号分量Ah和混响分量Ad，如式（9）所示，奇异值σ1、σ2体现了各分量的能量相对大小，这样便可以抑制混响背景能量，达到改善回波信混比的目的。

强混响背景下的回波检测问题可描述为

式中：s（t）是接收信号；x（t）是回波信号；r（t）是混响信号；n（t）是少量高斯白噪声；其中混响信号r（t）的能量远大于回波信号x（t）和高斯白噪声n（t）的能量。如果主动声纳接收到某段长为l的信号si，将其经过白化滤波器后得到信号γi，那么，可以将信号γi看成两部分的和，一部分为混响信号，另一部分为回波信号和高斯白噪声之和的线性叠加。将γi构造成式（8）所示的矩阵Ai，经过二分SVD分解后，信号被分解成两个子空间：

图1 信号矩阵中的各矢量Fig.1 Vectors of the signal matrix

为了获得信息完全的信号，对同一个数据的所有元素求平均，根据式（8）所示构造矩阵的方法，可以得到将混响分离后的信号γsi：

强混响背景下的宽带回波检测的整个过程可用图2描述。

图2 强混响背景下的宽带回波检测示意图Fig.2 Schematic diagram of broadband echo detection in strong reverberation background

一般情况下，通过一次二分SVD方法处理，便可以得到去除了大部分混响干扰的回波信号，如有必要，还可以对信号分量继续分解，以得到比较满意的分离信号。

综上所述，二分SVD方法抑制混响的原理清晰、实现简单，分离后得到的信号保持其在原信号中的相位，这是一般的滤波方法很难实现的。除此之外，该方法不需要各种法则估计信号子空间的维数，仅通过原信号中各分量的相对能量大小就实现了自动分离，大大减少了信号处理的复杂度。因此，相比于传统的预白化后直接匹配检测的方法，通过二分SVD方法进一步处理，在一定程度上改善了回波信混比，从而提高了匹配滤波器的检测性能。

4 仿真实验分析

本节通过仿真实验验证本文方法的有效性。设主动声纳发射频率为5～10 kHz的LFM信号，脉宽为10 ms，采样率25 kHz，按文献[20]所述方法产生如图3所示的混响信号，混响长度为2 s。将混响数据按发射信号脉宽等分为20段，求相邻各段的Itakura距离，如图4所示，相邻距离单元的Itakura距离都小于0.3，因此可认为相邻数据段混响满足局部平稳特性。不考虑脉冲展宽，在原混响数据的第30 250～30 300处叠加回波信号，文献[5]在信混比为-10 dB的条件下进行了仿真分析，验证了混响预白化可提高匹配滤波检测性能，为了更清楚地对比说明本文方法在低信混比条件下的检测优势，将信混比设为-15 dB。由于本文实质上探讨的是信混比对匹配检测器的影响，所以仿真中不再考虑多普勒运动对匹配滤波器检测性能的影响。

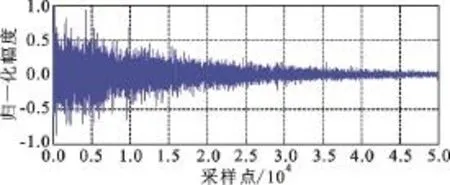
图3 混响仿真信号Fig.3 Simulative reverberation signal

图4 仿真混响的Itakura距离Fig.4 Itakura distance of simulative reverberation

截取包含回波信号的一段数据作处理，回波信号的起始位置在所取信号段的第1 501个采样点处，使用3种不同方法进行宽带回波检测，其中，图5为未白化直接匹配滤波的检测结果，图6是根据文献[5]中白化检测器的处理流程给出的经混响预白化后的匹配滤波结果，图7为使用本文方法先对混响预白化后的信号作一次二分SVD处理，再进行匹配滤波检测的结果。

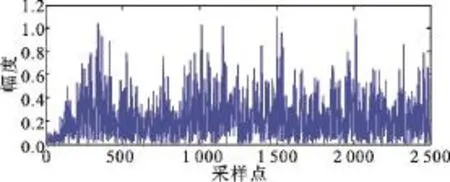
图5 未白化匹配滤波输出Fig.5 OutPut of matched filter Without being Whitened

图6 白化后匹配滤波输出Fig.6 OutPut of Whitened matched filter

图7 本文方法处理结果Fig.7 OutPut of Whitened matched filter using the ProPosed method

由图5～6可知，未白化匹配滤波检测器的峰值几乎淹没于附近的背景噪声干扰中，无法分辨回波检测相关峰，而经白化处理后，在1 251个采样点处有明显可分辨的峰值，但是由于原信号的信混比很低，即使经过了混响预白化处理，但背景噪声的干扰依然很严重，造成回波检测虚警过高，检测性能也不理想。由图7可以发现，经本文方法处理后，背景噪声能量被大幅削弱，信混比得到明显改善，回波检测相关峰清晰可见，取得了较好的信号检测效果。

在以混响为主要干扰时，环境噪声对主动声纳的性能影响相对较小，所以，在同等条件下，上述仿真中未考虑环境噪声并不影响性能对比。鉴于单次检测结果并不能充分说明问题，为了更全面分析本文方法的检测性能，在虚警概率不大于0.1的条件下，使用3种方法分别做1 000次蒙特卡洛仿真试验，得到不同信噪比条件下的检测概率曲线，如图8所示，可以发现，相比于文献[5]所述白化后的匹配滤波检测，本文方法可提高信混比约3 dB。随着信噪比降低，3种方法检测性能均逐渐恶化，在信混比为-15 dB时，白化后匹配滤波检测概率已低于0.6，但本文方法的检测概率仍高于0.7，因此，本文方法在低信混比条件下的检测性能优势相当明显。

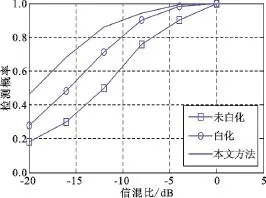
图8 3种方法检测性能对比Fig.8 ComParison of detection Performance among three methods

5 结束语

在强混响背景下，针对白化后匹配滤波器检测结果依然不理想的问题，本文提出一种改进方法，将白化后的信号先进行二分SVD处理，在一定程度上改善了信混比，然后再作匹配滤波检测。数值仿真和分析表明，在低信噪比条件下的检测性能优势明显，可提高匹配检测器的信混比约3 dB。本文方法不需要估计信号子空间维数，仅根据回波信号和混响的相对能量大小实现自动分离，原理清晰、实现简单，可在强混响背景下LFM信号回波检测中得到广泛应用。

本文方法在LFM信号的回波检测中取得了较好的效果，下一步将针对其他宽带信号进行深入研究，验证该方法在宽带信号中的普遍适应性。由于本文方法是在混响预白化的基础上作处理，假设混响是局部平稳的，对于混响在相邻数据段内非平稳的情况是否能拓展应用有待进一步研究。

[1] 曲振宇，陈励军.弹性物体在混响背景下的散射信号检测[J].电气电子教学学报，2007，29（1）：47-49. QU ZhenYu，CHEN Lijun.Scattering signal detection of e_ lastic object in reverberation noise[J].Journal of Electri_ cal＆Electronic Education，2007，29（1）：47-49.（in Chinese）

[2] 林静，王惠刚.混响背景下的距离扩展目标的GLRT检测[J].计算机仿真，2013，30（7）：179-182. LING Jing，WANG Huigang.GLRT detection of rangsPread targets in reverberation[J].ComPute Simulation，2013，30（7）：179-182.（in Chinese）

[3] KAY S，SALISBURG J.ImProved active sonar detection using autoregressive PreWhiteners[J].Journal of the A_ coustical SocietY of America，1990，87（4）：1603-1611.

[4] 李秀坤，夏峙，王向红，等.混响背景下水底目标回波盲分离[J].哈尔滨工程大学学报，2015，36（1）：62-67. LI Xiukun，XIA Zhi，WANG Xianghong，et al.Blind sePa_ ration of underWater target echoes in reverberation back_ ground[J].Journal of Harbin Engineering UniversitY，2015，36（1）：62-67.（in Chinese）

[5] 赵航芳，祝献，宫先仪.混响背景下的信号检测[J].哈尔滨工程大学学报，2004，25（1）：34-37. ZHAO Hangfang，ZHU Xian，GONG XianYi.Detection of signals in reverberation noise[J].Journal of Harbin Engi_ neering UniversitY，2004，25（1）：34-37.（in Chinese）

[6] 王平波，蔡志明.非高斯数据的高斯化滤波[J].声学与电子工程，2006，83（3）：26-30. WANG Pingbo，CAI Zhiming.Gaussianization filtering of non Gauss data[J].Acoustic and Electronic Engineering，2006，83（3）：26-30.（in Chinese）

[7] 宋世军.混响背景下目标回波的检测方法研究[D].哈尔滨：哈尔滨工程大学，2008：21-30. SONG Shijun.StudY the method of target echo detection under reverberation[D].Harbin：Harbin Engineering Uni_ versitY，2008：21-30.（in Chinese）

[8] 陈文剑，孙辉，朱建军，等.基于分数阶傅里叶变换混响抑制的目标回波检测方法[J].声学学报，2009，34（5）：408-415. CHEN Wenjian，SUN Hui，ZHU Jianjun，et al.A method for detecting target echo in reverberation based on frac_ tional Fourier transform[J].Acta Acustica，2004，25（1）：34-37.（in Chinese）

[9] 邓兵，陶然，齐林，等.分数阶Fourier变换与时频滤波[J].系统工程与电子技术，2004，26（10）：1357-1405. DENG Bing，TAO Ran，QI Lin，et al.Fractional Fourier transform and time-frequencY filtering[J].SYstems Engi_ neering and Electronics，2004，26（10）：1357-1405.（in Chinese）

[10] 邓兵，陶然，齐林，等.基于分数阶傅里叶变换的混响抑制方法研究[J].兵工学报，2005，26（6）：761-765. DENG Bing，TAO Ran，QI Lin，et al.A studY on anti-re_ verberation method based on Fractional Fourier transform [J].Acta Armamentarii，2005，26（6）：761-765.（in Chinese）

[11] 张宗堂，杨锡铅，戴卫国.混响背景下回波信号起始位置提取[J].舰船电子工程，2014，34（11）：73-79. ZHANG Zongtang，YANG Xiqian，DAI Weiguo.Pick-uP of echo starting location in reverberation[J].ShiP Elec_ tronic Engineering，2014，34（11）：73-79.（in Chinese）

[12] CARMILLET V，JOURDAIN G.LoW-sPeed targets so_ nar detection using autoregressive models in reverbera_ tion；exPerimental Performances for Wideband signals [C]//Proceedings of 1998 IEEE Oceanic Engineering SocietY Proceedings of the 1998 Oceans Conference.NeW York：IEEE，1998：1285-1289.

[13] 张贤达.现代信号处理[M].北京：清华大学出版社，1995. ZHANG Xianda.Modern signal Processing[M].Bei_ jing：Tsinghua UniversitY Press，1995.（in Chinese）

[14] 余义德，刘欣，李全琼.混响噪声局部平稳条件下次佳检测方法研究[J].微处理机，2013（3）：18-21. YU Yide，LIU Xin，LI Quanqiong.Research on second best detection method of reverberation noise under local stabilization[J].MicroProcessors，2013（3）：18-21.（in Chinese）

[15] 郑羽洁.改进的混响数据分段Itakura距离估计算法[J].科技通报，2014，30（10）：202-204. ZHENG Yujie.ImProved algorithm of PieceWise Itakura distance estimation With reverberation data[J].Bulletin of Science and TechnologY，2014，30（10）：202-204.（in Chinese）

[16] CARMILLET V，AMBLARD P O，JOURDAIN G.Detec_ tion of Phase or frequencY modulated signals in reverber_ ation noise[J].Journal of the Acoustical SocietY of A_ merica，1999，105（6）：3375-3389.

[17] 赵学智，叶邦彦，陈统坚.多分辨奇异值分解理论及其在信号处理和故障诊断中的应用[J].机械工程学报，2010，46（20）：64-75. ZHAO Xuezhi，YE BangYan，CHEN Tongjian.TheorY of multi-resolution singular value decomPosition and its aP_ Plication to signal Processing and fault diagnosis[J]. Journal of Mechanical Engineering，2010，46（20）：64-75.（in Chinese）

[18] 赵学智，叶邦彦.多分辨SVD包理论及其在信号处理中的应用[J].电子学报，2012，40（10）：2039-2046. ZHAO Xuezhi，YE BangYan.Multi-resolution SVD Packet theorY and its aPPlication to signal Processing [J].Acta Electronica Sinica，2012，40（10）：2039-2046.（in Chinese）

[19] 许策，赵相霞，章新华，等.混响背景下主动声纳接收信号的可分离性探讨[J].声学技术，2010，29（3）：327-330. XU Ce，ZHAO Xiangxia，ZHANG Xinhua，et al.The seP_ arabflitY of active sonar signals in the Presence of rever_ beration[J].Technical Acoustics，2010，29（3）：327-330.（in Chinese）

[20] 吴培荣，徐景峰.基于统计模型的混响信号仿真[J].声学技术，2013，32（6）：515-518. WU Peirong，XU Jingfeng.Reverberation simulation based on the statistical model[J].Technical Acoustics，2013，32（6）：515-518.（in Chinese）

舒象兰（1980—），男，湖南辰溪人，博士，讲师，主要研究方向为声纳信号处理和水下目标探测；

SHU Xianglan Was born in Chenxi，Hunan Province，in 1980.He is noW a lecturer With the Ph.D.degree.His research concerns sonar sig_ nal Processing and underWater target detection.

Email：shiftfeng_120@163.com

孙荣光（1975—），男，山东海阳人，副教授，主要研究方向为水声信号处理和声纳作战模拟；

SUN Rongguang Was born in HaiYang，Shandong Province，in 1975.He is noW an associate Professor.His research concerns acoustic signal Processing and sonar combat simulation.

马 鑫（1977—），男，山东微山人，副教授，主要研究方向为声纳信号处理和水声对抗。

MA Xin Was born in Weishan，Shandong Province，in 1977. He is noW an associate Professor.His research concerns sonar signal Processing and underWater acoustic countermeasure.

Echo Detection of LFM Signal under Strong Reverberation Background

SHU Xianglan，SUN Rongguang，MA Xin
（Naval Submarine AcademY，Qingdao 266199，China）

Reverberation is the main background interference in active sonar detection.Because the rever_ beration is a nonstationarY colored noise，Which degrades the Performance of the matched filter in White noise background.For the detection of target echo in reverberation background，the broadband echo is used to be Pre-Whitened With the Auto-Regressive（AR）model，hoWever，the result is not satisfYing under the background of strong reverberation.In order to solve the Problem，this PaPer ProPoses an imProved method on the basis of the AR model for Pre-Whitening Processing.The Whitened signal can be firstlY Processed bY Singular Value DecomPosition（SVD）to eliminate a majoritY of reverberation interference effectivelY，then the remained signal is disPosed With matched filter.Simulation and analYsis indicate the imProved method can enhance signal to reverberation ratio（SRR）about 3 dB comPared With traditional one，so it obviouslY imProves the Performance of matched filter.

active sonar；LFM signal；echo detection；strong reverberation；Pre-Whitening；matched filter；signal to reverberation ratio

The National High-tech R＆D Program of China（863 Program）

TN911

A

1001-893X（2016）01-0082-06

10.3969/j.issn.1001-893x.2016.01.015

舒象兰，孙荣光，马鑫.强混响背景下LFM信号回波检测[J].电讯技术，2016，56（1）：82-87.[SHU Xianglan，SUN Rongguang，MA Xin.Echo detection of LFM signal under strong reverberation background[J].Telecommunication Engineering，2016，56（1）：82-87.]

2015-06-23；

2015-11-25 Received date：2015-06-23；Revised date：2015-11-25

国家高技术研究发展计划（863计划）项目

**通信作者：shiftfeng_120@163.com Corresponding author：shiftfeng_120@163.com