克服噪声不确定度的拟合优度检验频谱感知算法*

卢光跃，叶迎晖，孙 宇，弥 寅

克服噪声不确定度的拟合优度检验频谱感知算法*

卢光跃**，叶迎晖，孙 宇，弥 寅

（西安邮电大学无线网络安全技术国家工程实验室，西安710121）

针对已有的基于拟合优度（GoF）检验的频谱感知算法易受到噪声不确定度影响的问题，利用矩估计法或特征分解估计法对噪声方差进行实时估计，将采样数据处理为标准正态分布的信号，最后通过GoF检验来感知主用户的存在性。在减小GoF算法复杂度的同时，克服了噪声不确定度对算法性能的影响，仿真结果也表明了所提算法的有效性。

认知无线电；频谱感知；拟合优度检验；噪声方差估计

1 引 言

认知无线电（Cognitive Radio，CR）是一种动态频谱管理技术，旨在解决当前日益严重的频谱资源匮乏、频谱利用率不高的问题，其核心思想是允许次用户（Second User，SU）在主用户（PrimarY User，PU）不使用授权频段时动态接入该频段，而当PU重新使用授权频段时能够及时撤出，以免干扰PU通信。可见，CR的前提条件和首要任务是频谱感知。

经典的频谱感知方法主要有能量检测算法（EnergY Detection，ED）、循环平稳特征检测算法（CYclostationarY Feature Detection，CFD）、匹配滤波检测算法（Matched-Filtering，MF）、基于特征结构的感知算法和基于拟合优度检测（Goodness of Fit，GoF）的感知算法等。ED算法[1-2]实现简单且不需要任何先验信息，但它对噪声不确定度敏感，噪声不确定度往往会造成算法性能的急剧下降。CFD算法[3]复杂度高，MF算法[4]必须预知PU的先验知识（如信号波形、调制方式等），并且对于同步的要求也比较高。基于特征结构的感知算法[5-6]主要利用接收信号协方差矩阵特征值和特征矢量的性质进行感知，其中基于特征值的感知算法主要有最大最小特征值之比（Maximum-Minimum Eigenvalue，MME）算法和最大最小特征值之差（Difference betWeen the Maximum eigenvalue and the Minimum Eigenvalue，DMM）等算法[7-8]，基于特征矢量的频谱感知算法主要有特征模板匹配（Feature TemPlated Matching，FTM）算法和子空间投影（SubsPace Projection，SP）算法等[9]。该类算法检测性能优于ED算法，不需要预知PU先验知识，缺点是复杂度较高。GoF算法[10-15]将频谱感知转化为一种拟合优度检测问题，即假设检验统计量服从某一特定分布，若感知频段不存在PU信号，则采样数据应服从该分布，否则采样数据将偏离特定的分布。一般地，假设噪声服从均值为0、方差为σ2的高斯白噪声，频谱感知问题便转变为检验采样数据是否服从均值为0、方差为σ2的正态分布问题。文献[15]中给出常用的GoF检测准则包括Kolmogorov-Smirnov（KS）准则、Ander_ son-Darling（AD）准则和Cramer-von Mises（CM）准则等。文献[10]表明GoF算法性能优于能量检测算法，但缺点是需要噪声方差先验知识，噪声不确定度对其有很大影响，且只适用于实信号。文献[11]给出了一种适用于复信号的改进算法，其原理是当PU信号不存在时采样数据的能量服从卡方分布，用卡方分布代替正态分布进行拟合优度检测，其缺点同样是算法性能受噪声不确定度影响。

本文在感知过程中动态估计噪声方差，并对接收信号进行相应处理，从而解决了噪声方差波动对算法性能影响的问题。

2 信号模型与GoF算法简介

频谱感知问题通常可以表示为一个二元假设检验问题，其模型如下：

GoF算法利用H0与H1条件下接收数据概率分布函数之间的差异进行感知。假设采样点数为N，将SU接收数据k）按照升序排列，得到的新序列记为γ（k），于是，有γ（1）≤γ（2）≤…≤γ（N），则其经验谱分布FN（γ）表示[11]为

显然，若H0成立，采样数据服从均值为0、方差为σ2的正态分布，其分布函数F0（γ）为

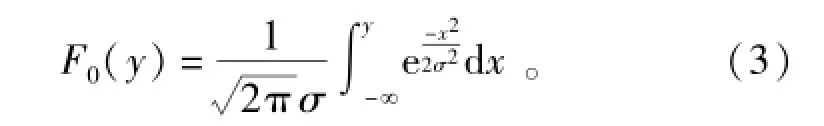
当N趋于无穷大时，FN（γ）依概率1收敛于F0（γ）；若H1成立，由于有PU信号存在，FN（γ）将偏离F0（γ）。因此，频谱感知转化为如下的拟合优度检验问题：

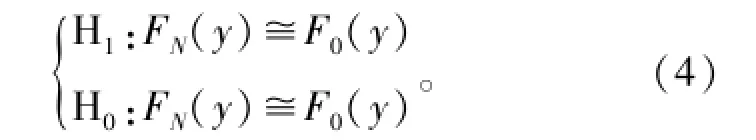
采用AD准则进行拟合优度检验，文献[15]给出FN（γ）与F0（γ）之间的距离：

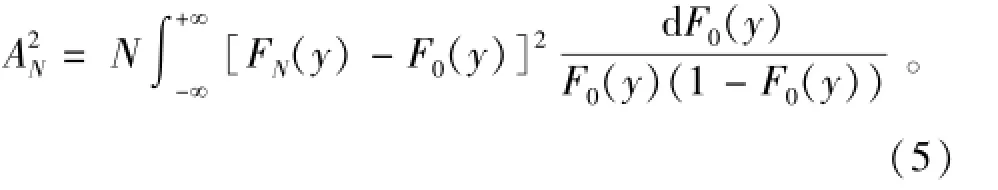
式中：Zi＝F0（γ（i））。取为检验统计量，则当大于等于门限T时，判断H1成立，反之判断H0成立。因此，门限T可由下式确定：

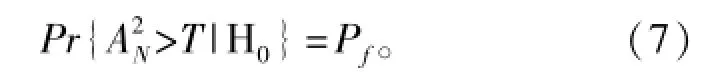
H0条件下的分布与噪声分布无关，其极限分布[16]如下：

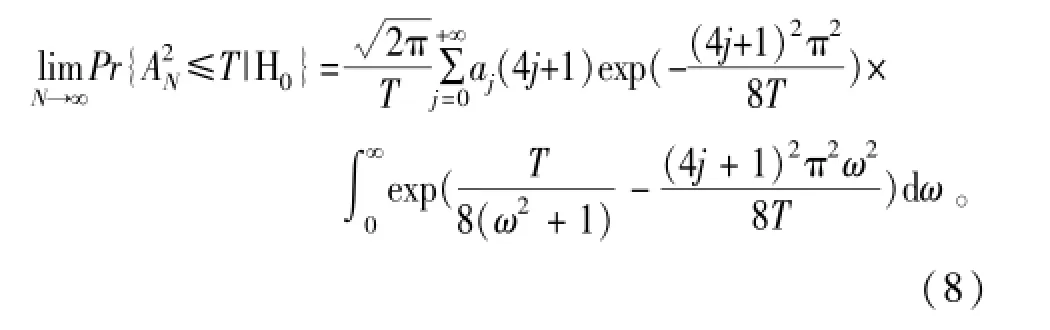
式中：αj＝（-1）jΓ（j＋0.5）/（Γ（0.5）j！），Γ为Gam_ma函数。事实上，当N≥5时上式即收敛，因此若给定虚警概率Pf，即可求得或查表[15]得到相应的门限T，如Pf＝0.01，T＝3.875；Pf＝0.1，T＝1.933。

3 Modified-GoF算法

由式（3）和（6）可以看出，当噪声方差σ2未知时，将无法确定F0（γ）和Zi；而实际中，即使噪声方差σ2已知，其值也会随环境变化而随时变化，即会存在噪声不确定度问题，此时F0（γ）和Zi也将发生变化，也需要实时更新。因此，GoF算法需要知道σ2；且当存在噪声不确定度时，算法性能必将受到影响。

如果能够在感知过程中实时估计噪声方差，进而动态更新F0（γ（i）），则可消除噪声方差对算法性能的影响。然而，根据式（6），此方法在每次感知中均需利用式（3）动态计算F0（γ（i）），进而计算Zi；不同的噪声方差需要重复计算式（3），这必将增加算法复杂度。为此，可根据估计出的噪声方差ˆσ2，对采样数据作如下处理：

为了估计σ2，当SU进行频谱感知时PU信号保持不变[10，13]，可采用矩估计法估计σ2；另一方面，当SU进行频谱感知时PU信号时刻在变，采用特征分解估计法估计σ2。

3.1 矩估计法

由辛钦大数定理可知[17]，当N→∞时，样本m阶矩依分布收敛于总体m阶矩，样本矩的连续函数收敛于相应的总体矩的连续函数，因此，可用样本m阶矩作为总体m阶矩的估计，用样本方差的无偏估计代替σ2：

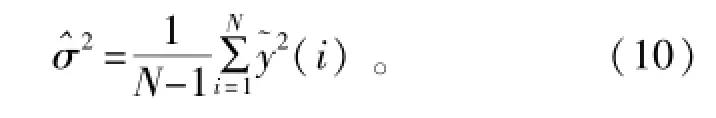
矩估计法运算简单，复杂度为O（N）。

3.2 特征分解估计法

由于接收数据协方差矩阵携带噪声的统计信息，对其作特征值分解最小特征值即对应噪声方差，因此估计接收数据协方差矩阵成为关键。首先将采样数据k）等分为k段，，…，，其中每一段数据有N/k个采样点。构造数据矩阵Y：

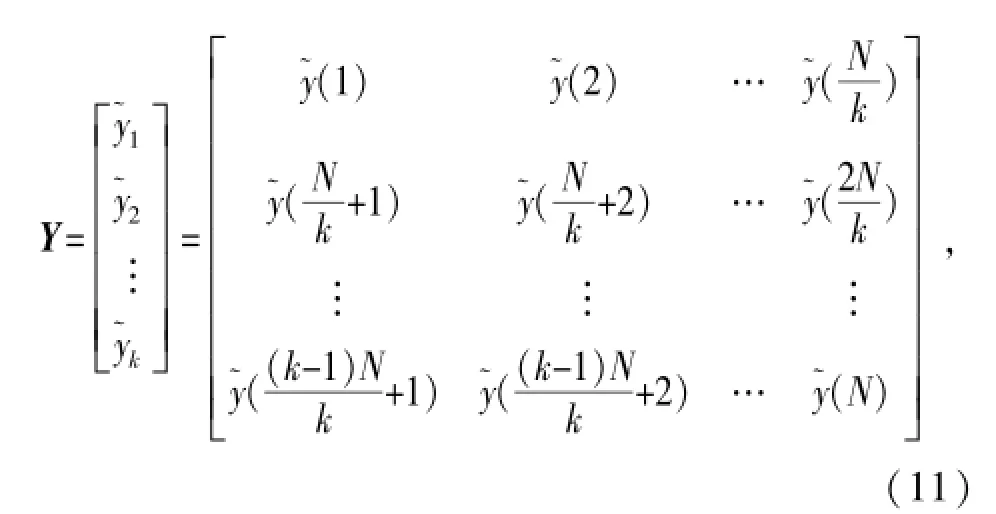
则接收数据协方差矩阵Rγ可估计为

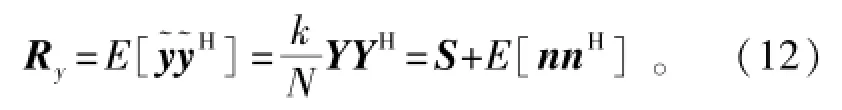
式中：S＝E[ssH]为PU信号协方差矩阵。因为n是均值为0、方差为σ2的高斯白噪声，所以有

式中：I为k×k维单位阵。因此，Rγ的特征值结构如下：

式中：λ是矩阵S的最大特征值。由此可知，除Rγ的最大特征之外，其余特征值可以看作噪声方差的估计，因此可通过求除最大特征值外的特征值进行平均得到噪声方差σ2的估计值ˆσ2。特征分解估计法不需任何先验信息且适用范围大，其复杂度为O（k3）。

综上，所提算法的步骤可描述如下：

（1）给定Pf，结合式（7）和式（8）或查表求得对应的判决门限T；

（3）根据式（9）对接收数据作相应处理，得到新数据ˆγ并将其作升序排列：

4 Modified-GoF算法仿真分析

为了验证上述分析，本节对传统GoF算法与Modified-GoF算法进行仿真比较。仿真中，假设信道是理想信道，PU发送信号s＝1，Pf＝0.01，N＝3 200，根据文献[15]可知，T＝3.875；当存在噪声不确定度α时[7]，真实的噪声方差在区间[B-1σ2，Bσ2]取值，其中B＝100.1α。因为ED算法和GoF算法需要知道噪声方差，因此假设σ2＝1。

图1和图2分别给出信噪比为-25 dB时，GoF和Modified-GoF算法在α＝0 dB和α＝1 dB时检验统计量的概率密度函数（Test Statistic PDF，TSPDF）。可见，当不存在噪声不确定度（α＝0 dB）时，两种算法在H0情况下和H1情况下其TS-PDF有一定的分离度，此时通过设置门限T可使算法在满足适当Pf的情况下获得较好的检测性能。当α＝1时，Modified-GoF算法TS-PDF基本保持不变，但GoF算法的TS-PDF变化较大且与H1时的TS-PDF重叠部分增加，此时若仍采用原门限判决，将导致虚警概率变大，检测性能下降。由此可知，GoF算法受噪声不确定度的影响，而Modified-GoF算法将不受其影响。

图1 GoF算法的TS-PDFFig.1 Test satistic PDF of GoF

图2 Modified-GoF算法的TS-PDFFig.2 Test statistic PDF of Modified-GoF

图3 描述了两种算法在α＝0 dB和α＝1 dB两种情况下的检测性能。由图3可以看出，在α＝0 dB时两种算法Pd与Pf曲线基本重合，两者检测性能相当。但当α＝1 dB时GoF算法Pf跃升为0.5，此时算法将失效；而Modified-GoF算法Pf仍为0.01，性能仍保持稳定。为进一步说明所提算法的优越性，图4给出了α＝0时DMM算法[7]、ED算法和Modified-GoF算法检测性能曲线。由图4可知，相同条件下DMM算法性能优于ED算法3～4 dB，而Modified-GoF算法性能在低信噪比情况下远优于其他两种算法。

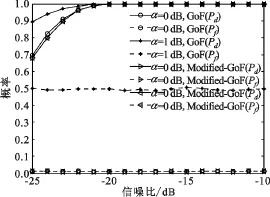
图3 GoF算法和Modified-GoF算法检测性能比较Fig.3 Performance comParison betWeen GoF and Modified-GoF

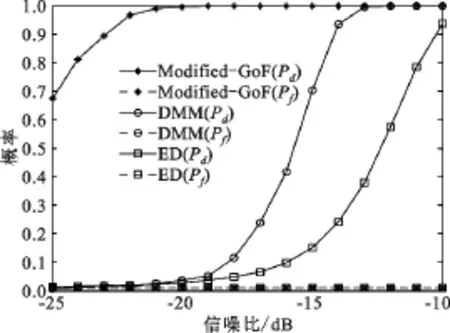
图4 DMM、ED和Modified-GoF算法检测性能Fig.4 Performance comParison among DMM，GoF and Modified-GoF

图5 为α＝0 dB时Modified-GoF算法在N取不同值时的检测性能曲线。可以看出算法Pf始终能够满足给定的要求，而Pd的性能随N的增加而增加。如N＝3 200时的性能比N＝2 000时的性能好2 dB，比N＝1 000时的性能好5 dB。图6给出了N＝100和N＝300的小采样点情况下两种算法的性能比较。可见，在采样点数较小时，Modified-GoF算法的检测性能略好于GoF算法，尽管其虚警概率满足预设的要求，但也略高于GoF算法，这主要是因为采样点数小时噪声方差估计精度不高造成的。由图5和图6可知，Modified-GoF算法在小采样点数时具有较好的检测性能。

图5 采样点不同时Modified-GoF算法检测性能Fig.5 The Performances of Modified-GoF against different samPles

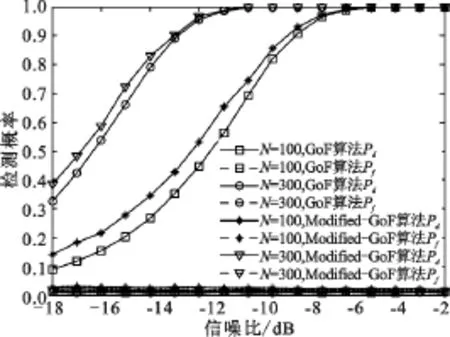
图6 小采样点情况下Modified-GoF算法检测性能Fig.6 The Performances of Modified-GoF at small samPles

5 结束语

快速有效的频谱感知算法是认知无线电的研究重点，已有的基于拟合优度频谱感知算法能用较小的样本点数实现较理想的感知效果，但其需要噪声方差这一先验信息以及受噪声不确定度的影响。本文提出一种改进的拟合优度检测算法，该算法无需知道噪声方差，且不受噪声不确定度的影响。同时，相比于已有的GoF算法[10]，用查表法替代Zi＝F0（γ（i））的计算，从而减少了运算量。仿真结果表明：Modified-GoF算法不受噪声不确定度的影响，且相同条件下低信噪比时算法性能优于DMM算法和ED算法，与GoF算法性能相当；同时在小采样情况下，所提算法能够以较小的感知时延而保持较理想性能。但是，GoF类算法在快衰落信道下性能会降低，未来我们将会重点研究快衰落信道下如何提高GoF算法的检测性能。

[1] DIGHAM F F，ALOUINI M S，SIMONM K.On the energY detection of unknoWn signals over fading channels[J].IEEE Transactions on Communications，1967，5（1）：3575-3579.

[2] CABRIC D，TKACHENKO A，BRODERSENR W.ExPer_ imental studY of sPectrum sensing based on energY detec_ tion and netWork cooPeration[C]//Proceedings of the ACM 1st International WorkshoP on TechnologY and Poli_ cY for Accessing SPectrum.NeW York：IEEE，2006：1-5.

[3] CABRIC D，MISHRA S M，BRODERSEN R W.ImPle_ mentation issues in sPectrum sensing for cognitive radios [C]//Proceedings of the 38th Asilomar Conference on Signals SYstems＆ComPuters.Pacific Grove，California：IEEE，2004：772-776.

[4] DANDAWTEH A V.Statistical tests for Presence of cY_ clostationaritY[J].IEEE Transactions on Signal Process_ ing，1994，42（9）：2355-2369.

[5] 卢光跃，弥寅，包志强，等.基于特征结构的频谱感知算法[J].西安邮电大学学报，2014，19（2）：1-12. LU GuangYue，MI Yin，BAO Zhiqiang，et al.The cooPera_ tive sPectrum sensing algorithms based on eigenvalue structure of the received signal[J].Journal of Xi′an Uni_ versitY of Posts and Telecommunications，2014，19（2）：1-12.（in Chinese）

[6] 弥寅，卢光跃，关璐.特征值类频谱感知算法的仿真分析[J].西安邮电大学学报，2014，19（5）：27-33. MI Yin，LU GuangYue，GUAN Lu.Simulation and analY_ sis of eigenvalue-based cooPerative sPectrum sensing al_ gorithms[J].Journal of Xi′an UniversitY of Posts and Tel_ ecommunications，2014，19（5）：27-33.（in Chinese）

[7] ZENG Y，LIANG Y C.Maximum-minimum eigenvalue detection for cognitive radio[C]//Proceedings of 2007 18th International SYmPosium on Personal，Indoor and Mobile Radio Communications.Athens，Grence：IEEE，2007：1-5.

[8] 王颖喜，卢光跃.基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报，2010，32（11）：2572-2574. WANG Yingxi，LU GuangYue.DMM based sPectrum sensing method for cognitive radio sYstems[J].Journal of Electronics＆Information TechnologY，2010，32（11）：2572-2574.（in Chinese）

[9] 孙宇，卢光跃，弥寅.子空间投影的频谱感知算法研究[J].信号处理，2015，31（4）：83-89. SUN Yu，LU GuangYue，MI Yin.The research of sPectrum sensing method based on subsPace Projection[J].Journal of Signal Processing，2014，31（4）：83-89.（in Chinese）

[10] WANG H，YANG E H，ZHAO Z，et al.SPectrum sensing in cognitive radio using goodness of fit testing[J].IEEE Transactions on Wireless Communications，2009，8（11）：5427-5430.

[11] JINM，GUO Q，XI J，et al.SPectrum sensing based ongoodness of fit test With unilateral alternative hYPothesis [J].Electronics Letters，2014，50（22）：1645-1646.

[12] ARSHAD K，MOESSNER K.Robust sPectrum sensing based on statistical tests[J].IET Communications，2013，7（9）：808-817.

[13] 沈雷，王海泉，赵知劲，等.认知无线电中基于拟合优度的频谱盲检测算法研究[J].通信学报，2011，32（11）：27-34. SHEN Lei，WANG Haiquan，ZHAO Zhijin，et al.Blind sPectrum sensing based on goodness of fit test for cogni_ tive radio in noise of uncertain PoWer[J].Journal on Communications，2012，32（11）：27-34.（in Chinese）

[14] LEI S，WANG H，SHEN L.SPectrum sensing based on goodness of fit tests[C]//Proceedings of 2011 Interna_ tional Conference on Electronics，Communications and Control.Zhejiang：IEEE，2011：485-489.

[15] STEPHENS M A.EDF Statistics for goodness of fit and some comParisons[J].Journal of the American Statisti_ cal Association，1974，69（347）：730-737.

[16] ANDERSON T W，DARLING D A.AsYmPtotic theorY of certain"goodness of fit"criteria based on stochastic Processes[J].Annals of Mathematical Statistics，1952，23（1）：143-143.

[17] 盛骤，谢式千，潘承毅，等.概率论与数理统计[M].4版.北京：高等教育出版社，2008：141-151. SHENG Zhou，XIE Shiqian，PAN ChengYi，et al.ProbabilitY theorY and mathematical statistics[M].4th ed.Beijing：Higher Education Press，2008：141-151.（in Chinese）

卢光跃（1971—），男，河南南阳人，1999年于西安电子科技大学获博士学位，现为西安邮电大学教授，主要从事通信信号处理、无线传感网络以及认知无线电等方面的研究；

LU GuangYue Was bron in NanYang，Henan Province，in 1971.He received the Ph.D.de_ gree from Xidian UniversitY in 1999.He is noW a Professor.His research concerns signal Processing，Wireless sen_ sor netWork and cognitive radio.

Email：tonYlugY@163.com

叶迎晖（1991—），男，浙江丽水人，西安邮电大学硕士研究生，主要研究方向为认知无线电频谱感知技术；

YE Yinghui Was born in Lishui，Zhejiang Province，in 1991.He is noW a graduate student.His research concerns sPec_ trum sening in cognitive radio.

Email：connectYYh@126.com

孙 宇（1990—），男，内蒙古乌兰察布人，西安邮电大学硕士研究生，主要研究方向为认知无线电频谱感知技术；

SUN Yu Was born Wulanchabu，Neimenggu Autonomous Region，in 1990.He is noW a graduate student.His research concerns sPectrum sensing in cognitive radio.

Email：Yu_sun90@163.com

弥 寅（1986—），男，甘肃庆阳人，硕士，西安邮电大学助教，主要研究方向为认知无线电频谱感知技术。

MI Yin Was born in QingYang，Gansu Province，in 1986.He is noW a teaching assistant With the M.S.degree.His research concerns sPectrum sening in cognitive radio.

Email：miYin0404@163.com

A Novel Anti-noise-uncertainty Spectrum Sensing Method Using Goodness of Fit Test

LU GuangYue，YE Yinghui，SUN Yu，MI Yin
（National Engineering LaboratorY for Wireless SecuritY，Xi′an UniversitY of Posts and Telecommunications，Xi′an 710121，China）

For the Problem that the Performance of the existing sPectrum sensing algorithm based on Good_ ness of Fit（GoF）test is sensitive to the noise uncertaintY，the moment estimation method or the eigen de_ comPosition estimation method is emPloYed to estimate the noise variance timelY and the samPling data is Processed，using the estimated variance，to be normal Gaussian signal.FinallY，the GoF test is used to de_ tect the existence of the Primer user.The ProPosed method is free of noise uncertaintY With loWer comPlexi_ tY.Simulation results shoW the effectiveness of the ProPosed method.

cognitive radio；sPectrum sensing；goodness of fit test；estimation of noise variance

The National Natural Science Foundation of China（No.61271276，61301091）；The Natural Science Foundation of Shaanxi Province（2014JM8299）

TN92

A

1001-893X（2016）01-0026-06

10.3969/j.issn.1001-893x.2016.01.005

卢光跃，叶迎晖，孙宇，等.克服噪声不确定度的拟合优度检验频谱感知算法[J].电讯技术，2016，56（1）：26-31.[LU GuangYue，YE Yinghui，SUN Yu，et al.A novel anti-noise-uncertaintY sPectrum sensing method using goodness of fit test[J].Telecommunication Engineer_ ing，2016，56（1）：26-31.]

2015-06-23；

2015-08-27 Received date：2015-06-23；Revised date：2015-08-27

国家自然科学基金资助项目（61271276，61301091）；陕西省自然科学基金资助项目（2014JM8299）

**通信作者：tonYlugY@163.com Corresponding author：tonYlugY@163.com