考虑空箱调运的远洋班轮航线优化

李 建，韩晓龙

(上海海事大学科学研究院， 上海201306)



考虑空箱调运的远洋班轮航线优化

李 建，韩晓龙

(上海海事大学科学研究院， 上海201306)

全球集装箱运输市场持续低迷环境下，各大航运公司不得不采取各种手段来控制成本，提高经营效益。为设计更加合理的运输航线以节省班轮公司运营成本，从班轮公司的角度出发，以新的角度来选择航线，考虑空箱调运对于航线成本的影响，建立以每周运营总成本最小化为目标的班轮航线优化模型，设计了有效的启发式算法来解决空箱调运问题；通过在不同地区设置不同数量的二次挂靠港，计算总成本选出最小的航线结构。并通过美西南航线的案例分析表明，当设置一个位于北美的港口作为二次挂靠港时，可以使得班轮公司周运营成本降低2.52%。说明考虑了空箱调运的远洋班轮航线的优化可为班轮公司节省可观的运营成本。

集装箱；航线；空箱；启发式算法

0 引 言

航线设计问题属于集装箱班轮公司的战略问题，班轮公司的所有运输配置等方案都是基于已有航线进行的。航线的合理性对班轮公司的成本及收益具有至关重要的影响。

因此，近年来关于航线设计相关的研究较多，如：Baird[1]就航线设计问题和班轮班期的设置建立了多目标模型，确定了运输成本以及库存持有成本的函数关系；Bronmo等[2]针对传统的航线网络，采用启发式算法进行求解，建立“中心-分支”结构模型；Hsu等[3]针对轴辐式航线网络，建立了以运营成本和库存成本为最小的的双目标模型，研究直运和转运问题，求解出最佳航线和相应的船型配置、发船频次；Yan等[4]针对集装箱转运方案和短期的船舶调度问题，利用拉格朗日松弛、次梯度方法等求解，采用网络流技术建立了相关模型；Agarwal等[5]针对港口挂靠顺序和船队规模优化问题，采用时间拓扑理论，建立了相关模型；Imai等[6]针对班轮公司，基于环绕式和单摆式混合结构设计航线，虽考虑了空箱运输问题，但并未考虑重箱的运输；Kosmas等[7]利用模拟退火算法对航线运营成本问题进行求解，采用统计学方法对结果进行探讨，并将研究散货和邮轮运输的思想运用到航线设计中来；郭子坚等[8]针对空重箱的混合运输问题，建立了海运网络优化模型，优化了航线结构、空箱调运方案、班轮服务频次及船舶配置等问题；计明军等[9]研究了轴辐式集装箱运输网络，建立了基于混合整数规划的支线集装箱运输模型，同时在模型中考虑了船舶装载量和船舶在枢纽港的停泊时间等限制因素；陈康等[10]针对混合型航线结构，采取遗传算法进行求解，并建立了优化航线和空重箱运输方案的双层规划模型。

由于国际贸易的不平衡，空箱调运成为航运公司不可避免的非生产性经营活动，并在整个运输成本中占有较高的比重。因此，国内外学者针对空箱调运问题进行了大量研究。如：Moon[11]为了减少各港口集装箱不平衡的问题，优化了空箱的分配，研究的目标是极小化以装卸成本、运输成本和持有成本为代表的总成本；Song等[12]研究目的港不确定情况下的空箱流动方向，并采用仿真的技术对空箱调运方案进行评价以论证其有效性；杨洋[13]研究在多式联运下，运输过程中相关的班轮公司将空箱无偿提供给各方使用，前提是保证重箱的运输，从而一方面保证空箱的需求，另一方面也优化了总成本；韩晓龙等[14]研究了航运公司在新开发港口的集装箱空箱的分配问题，并通过分析发现在融资能力允许的情况下，自购箱是航运公司第一首选，但结合现实情况，自购箱和租箱混合才是基本策略。

可以发现，在以往的航线设计相关研究中，班轮航线优化通常从班期设置、船舶配置、枢纽港选择等方面着手；主要考虑枢纽港的选择、港口挂靠顺序、船舶的配置等问题，较少考虑空箱调运因素，但由于空箱调运成本在整个集装箱运输中占据了超过20%的成本，因此考虑了合理的空箱调运策略的航线设计能够为班轮公司节省巨大的成本，具有十分实际的应用价值。本文在优化船舶数量和配置的同时，将空箱调运对航线的影响考虑进来，在不同的空箱调运策略下选择出合适的回程挂靠港。

1 问题描述

一条远洋航线可以被看作包括了两个末端港口，即首端港和尾端港，这就包含了两个方向的港口序列。港口挂靠顺序从首端港至尾端港方向，称之为出境航向，反之则是入境航向。可以假设：若有两个港口在出入境航向中都作为挂靠港，则两者在两次航行的挂靠方向正好相反，且称此类港口为“二次挂靠港”。图1中包含两个二次挂靠港，它们将整个航线分为了3个闭环。

本文研究的问题是从班轮运输公司的角度考虑设计一条远洋运输航线，目标是服务于两个不同洲的多个港口，港口的集合用Ω表示，用|Ω|示集合内的元素个数。从给定的港口集合中，根据最短路径原则及各港口之间的的运输需求，确定合适的空箱调运策略，并设计有效的启发式算法来调配空箱，选出最优二次挂靠港，设计出使得每周的运营总成本最小的航线。

图1 航线运输结构图

2 模型建立

假设班轮运输的成本组成包括：船舶固定成本、燃料成本、港口挂靠费、装卸费、空重箱持有成本。这里需要指出的是，不同的空箱调运策略其影响并非仅仅表现在某一方面，它对整个航线中的各个环节都是有影响的。不同策略使得港口内集装箱装卸成本、在港停靠时间、空重箱运输时间等都会有所不同。在建立模型时，虽然其中并不会明确写有空箱调运成本这一项，但是在计算其中的每一项成本时，都需要建立在既有空箱调运策略的基础上。根据所假设的班轮运输成本组成建立如下班轮公司每周运营总成本函数见式(1)：

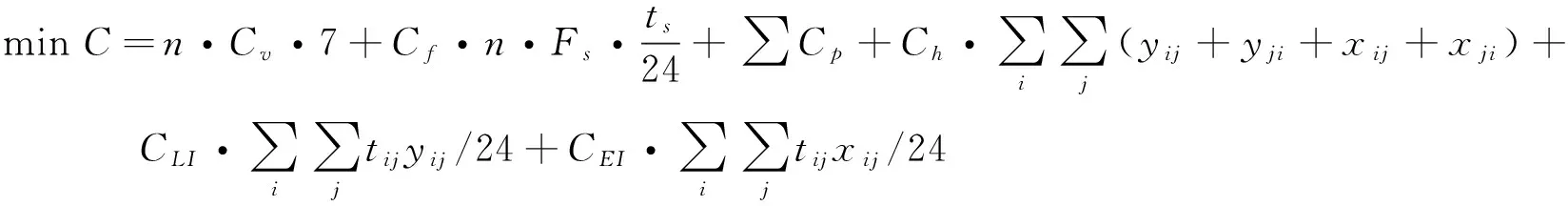
(1)

(2)

(3)

xij≥0,

(4)

其中:n为航线内配置的船舶数量，Cv为每艘船舶的日固定成本，Cf为单位燃料成本，Fs为一艘船舶海上每日燃料消耗量，Cp为港口固定挂靠费用，Ch为每标箱装卸费用，ts为每周海上航行总时间，tp为每周在港总时间，xij为港口间每周空箱运输量，yij为港口间每周重箱运输量，tij为港口间运输时间，CLI/CEI为单位重箱/空箱每日持有成本，p(i)为挂靠序号为i的港口，N为挂靠港口总次数，θv为船舶运力；决策变量为n，xij，θv。

在式(1)的右边，第一项表示船舶每周固定成本，第二项表示每周燃料成本，第三项表示每周港口固定挂靠成本，第四项表示每周集装箱装卸总成本，第五项表示重箱每周平均持有成本，第六项表示空箱每周平均持有成本。约束方程(2)保证了各港口集装箱输入、输出量平衡，约束方程(3)表示任意航段内集装箱装载量不超过船舶运力，约束方程(4)表示任意航段内空箱运输量为非负。

3 模型求解

在所建立的目标函数中，决策变量为n，xij，θv。该模型的求解思路是先根据最短路径原则和应用实际确定可能的航线结构，然后根据各港之间的需求确定相应结构下所选船舶船型θv及空箱调运策略xij，在此基础上，根据航行和在港时间，为保证每周一班的运输频次从而决定航线内应配置的船舶数量n，最后便是计算各航线结构对应的总成本，选择使得每周运营总成本最小的航线结构。

在组成空箱调运的成本当中，占据比例最大的是在港口的集装箱装卸成本，这是因为空箱运输一般都是利用班轮公司自有船舶的过剩运力来实现的。因此，在优化空箱调运成本时，应将减少集装箱装卸次数作为优先优化的因素。

在某个航段中，若船上的重箱装载率是整个航行途中最高的，则将该航段记为δ。若航线为多闭环航线结构，且空箱调运满足每个港口的空重箱流量平衡，则有推论：每个闭环内不同航段的集装箱总装载量相同，不同闭环的航段集装箱装载总量不一定相等；空箱调运策略可以由每个港口的净进口量来确定，且每个航段的集装箱总装载量等于重箱装载量最大航段的重箱装载量。为解决空箱调运问题，设计了有效的启发式算法，为了叙述简便，首先引入如下符号：

LVi(EVi):船舶由i港开往i+1港的过程中船上所装载的重箱(空箱)量;

LUi(EUi):船舶在i港时卸下的重箱(空箱)量;

LLi(ELi):船舶在i港时装运的重箱(空箱)量;

LFi(EFi):船舶由i港开往i+1港的过程中船上的重箱(空箱)装载量;

TFi:船舶由i港开往i+1港的过程中船上集装箱总的装载量。

若p(j)是二次挂靠港，j则是其中的一次挂靠序号，我们将另外的一次挂靠序号表示为j′，那么则有：p(j)′=p(j),j≠j′.用TVj:=LVj+EVj表示船舶在航段j[即p(j)开往p(j+1)]航行过程中的集装箱总量,EVj′表示船舶在航段j时装载空箱数量的最小值；假设首端港在航线的最左端。

步骤1 先确定在未考虑空箱调运时的重箱相关数据：yij,LVj。

步骤2 基于LVj和输入输出量平衡来求出最小空箱流量：

①数据初始化：令EVj′=0；

②平衡任意港口p(j)集装箱输入输出量：

若p(j)不是二次挂靠港，则EVj′=max{EVj′,LVj-1-LVj};

若p(j)是二次挂靠港，则平衡输入和输出p(j)的集装箱量，即：航段j的空箱量[从p(j)运出至p(j+1)]，以及航段j′-1的空箱量[从p(j′-1)运进至p(j′)=p(j)]；

EVj=max{0,LVj′-1-LVj};EVj′-1′=max{EVj′-1′,LVj-LVj′-1}。

步骤3 基于LVj和EVj来求出每个闭环内的TVj(注意：除了两端的闭环内均只有一个二次挂靠港以外，其他闭环内都含有两个二次挂靠港)。

若某闭环内有两个二次挂靠港p(j)和p(k),且j

若p(j)是最左端闭环内的二次挂靠港且j

若p(j)是最右端闭环内的二次挂靠港且j>j′,则：

TVj=max{LVm+EVm′|j≤m

步骤4 调整最小空箱运输量值：对于任意j,EVj′=max{EVj′,TVj-LVj}。

步骤5 计算每个航段的实际空箱运输量，从δ航段开始进行迭代,将所有二次挂靠港都标记为待处理港口：

①对于航段k=δ,设置EVδ=0,令k=k+1;

②令j=kmodn,使得0≤j

③若p(j)是非二次挂靠港，令EVj=LVj-1+EVj-1-LVj;

④若p(j)是待处理的二次挂靠港，则

首先计算出境航行时从p(j)运出的空箱量，即：EVj′=LVj-1+EVj-1-LVj′;

然后，根据其空箱的净进口量或净剩余量来确定EVj的值:

若p(j)是有空箱剩余的二次挂靠港，则:EVj=max{EVj′，EVj-1},这样船就不会在p(j)时又卸下空箱;

若p(j)是空箱量不足的二次挂靠港，则:EVj=max{EVj′,EVj-1+NetImport};

最后，满足船舶装载能力约束：EVj=min{EVj,θv-LVj};

⑤将p(j)标记为已处理港口;

⑥令k=k+1若k<δ+N,执行步骤5-② ;否则，执行步骤6(此步骤确保了船舶运力满足约束条件，在一个并没有空箱需求量的二次挂靠港，依然会有卸下空箱的可能)。

步骤6 计算每个港口空箱的装卸量，对于每个j，令ELj=max{0,EVj-EVj-1}且EUi=max{0,EVj-1-EVj}。

步骤7 求解具体空箱调运数据：

①从航段k=δ开始;

②令j=kmodn,使得0≤j

③令m=j+1;

④若ELj≤0,执行步骤7-⑥；

⑤若EUm>0,xjm=min{ELi,EUm},ELi=ELi-xjm,EUm=EUm-xjm;m=m+1,执行步骤7-④；

⑥k=k+1;若k<δ+N，执行步骤7-②；否则，执行步骤8。

步骤8 输出{yij,xij}；结束。

以上算法的优点表现在两个方面：第一，在最小化空箱装卸次数和空箱流量后即可直接得到最优或接近最优的调运策略；第二，该算法满足约束(3)，运用时不用首先确定船舶数量和航速。

4 算例分析

以某班轮运输公司经营的一条美西南航线为例，航线内共8个港口(其中亚洲5个，北美洲3个)，该航线目前的挂靠顺序是：新加坡—香港—盐田—宁波—上海—西雅图—奥克兰—长滩(—新加坡),无二次挂靠港。港口对间的距离以及需求量分别由表1及表2给出。

表1 港口对间的距离

表2 港口对间的每周需求量 标箱

假定同一地区/洲的港口之间没有需求量,各港口空箱来源均只由系统内部港口提供(也就是保证每个港口的集装箱输入和输出平衡),设定参数：各港口挂靠费相同，为平均2 000美元/次，船速为15 n mile/h，单位燃料费用600美元/吨，海上每日燃料消耗量为300吨，重箱持有成本25美元/d，空箱持有成本10美元/d，进港等待和离港时间均为2 h，装卸效率各港相同，为200个/h，集装箱装卸费100美元/TEU。

当亚洲港口所有重箱均装载完毕并开始运往北美时，航段内重箱运输量达到最大值，为10 800 TEU，因此选定船舶船型θv=11 000 TEU, 设定一艘11 000 TEU型船舶的每日固定成本为25 000美元/d。使用MATLAB编程软件进行计算，表3给出了相关计算结果。

表3中,λ,μ分别表示在北美洲和亚洲设定的二次挂靠港数量，因为亚洲和北美洲港口数量分别为5个和3个，同时首端港和尾端港又不会作为二次挂靠港，因此λ的可能值为0，1，2；μ的可能值为0，1，2，3，4。Q则表示每种结构下的不同挂靠方式的航线数量，表3中其他数据选择的是这些不同挂靠方式中使得每周运营总成本最小的一组。T是一个航次的航行总时间(d)，n则是根据航行总时间和为保证每周一班发船频次而确定的船舶数量。C为计算出来的每周运营总成本(单位：万美元)，最小值为 1 635.55万美元，而原始航线则为1 677.83万美元，优化后的周运营总成本可节省42.28万美元，节省幅度为2.52%。图2和图3分别是原始航线和优化航线的各航段空重箱装载情况。

图2 原始航线空重箱装载量

图3 优化后航线空重箱装载量

从图2和图3中可以看到，在保证每个港口的集装箱输入和输出平衡的约束条件下，原始航线每个航段内集装箱装载总量始终与最大重箱装载量相等，为10 800 TEU；而优化后的航线中，仅有奥克兰被挂靠了两次，根据航线结构设定可知有一个二次挂靠港的航线含有两个闭环，两个闭环内的集装箱装载总量分别为10 800 TEU(即闭环：新加坡—香港—盐田—宁波—上海—西雅图—奥克兰—新加坡)和6 328 TEU(即闭环：奥克兰—长滩—奥克兰)；这也同时证明了“3 模型求解” 部分所述所述的对于港口集装箱输入输出平衡条件下的推论，即：航线内每个闭环内不同航段的装载总量是相等的，而不同闭环的航段并不一定相等。

5 结 论

实验结果表明，本文建立的模型在应用中是简便可行的；优化后的航线含有一个二次挂靠港，为奥克兰，对应的航线挂靠顺序为：新加坡—香港—盐田—宁波—上海—西雅图—奥克兰—长滩—奥克兰—新加坡；设定船型θv=11 000 TEU，优化后的航线运营成本相比初始航线每周运营总成本节省2.52%。本文采用二次回程挂靠港的选择来设计航线结构，大大降低了计算量，为今后以新的角度来设计航线提供参考。下一步研究的目标是将船速、班期设置等问题进行优化也考虑到模型中来，以及考虑沿途挂靠港口涉及3个不同大陆的复杂情况。

[1] BAIRD A.Optimizing the container transshipment hub location[J]. Journal of transport geography, 2006,14：195-214.

[2] BRONMO G，CHRISTIANSEN M，FAGERHOLT K，et al.A multi-start local search heuristic for ship scheduling——a computational study[J]. Computers and Operations Research, 2007,34(3): 900-917.

[3] HSU C, HSIEH Y.Routing ship size and sailing frequency decision-making for a maritime hub-and-spoke container network[J]. Mathematical and Computer Modeling, 2007,45(7/8):899-916.

[4] YAN S, CHEN C, LIN S.Ship scheduling and container shipment planning for liners in short-term operations[J]. Journal of Marine Science and Technology, 2009,14(4):417-435.

[5] AGARWAL R, ERGUN O.Ship scheduling and network design for cargo routing in liner shipping[J]. Transportation Science, 2008,42(2): 175-196.

[6] IMAI A, SHINTANI K, PAPADIMITRIOU S.Multi-port vs.Hub-and-Spoke port calls by containerships[J]. Transportation Research Part E: Logistics and Transportation Review, 2009,45(5):740-757.

[7] KOSMAS O T, VIACHOS D S.Simulated annealing for optimal ship routing[J]. Computers and Operations Research, 2008,35(3):576-581.

[8] 郭子坚,王文渊,唐国磊,等.空重箱混合运输条件下集装箱海运网络优化研究[J]. 武汉理工大学学报(交通科学与工程版)，2013,37(2):343-347.

[9] 计明军，陈哲，王清斌.集装箱船舶支线运输航线优化算法[J]. 交通运输工程学报，2011,11(4)：68-75.

[10]陈康，郭利泉，杨忠振.基于混合航线结构的集装箱航线与空重箱运输综合优化模型[J]. 系统工程理论与实践，2014,34(1):122-128.

[11]MOON I K, NGOC A D D, HUR Y S.Positioning empty containers among multiple ports with leasing and purchasing considerations[J]. OR Spectrum, 2010,32(3): 765-786.

[12]SONG D P, DONG J X.Effectiveness of an empty container repositioning policy with flexible destination ports[J]. Transport Policy, 2011,18(1): 92-101.

[13]杨洋.基于集装箱资源共享的班轮公司空箱调运优化模型[J]. 东华大学学报(自然科学版)，2010,36(5): 581-587.

[14]韩晓龙, 种道坤.船公司在新港口上的空箱分配策略[J]. 广西大学学报(自然科学版)，2016,41(3):738-744.

(责任编辑 梁 健)

The overseas liner route optimization with considering empty container repositioning

LI Jian, HAN Xiao-long

(Scientific Research Institute，Shanghai Maritime University，Shanghai 201306，China)

The global container transportation market has been relatively downturn, many shipping companies have to take different measures to reduce their operation costs in order to maintain the normal operation of the company. In order to design an optimal shipping route and to reduce the operating costs, a new perspective of selecting route, and considering empty container transportation for the cost impact is proposed and a mathematical model from shipping company’s point of view, which aims to minimize the total weekly operating costs, is established. And also, an efficient heuristic algorism to optimize the empty container repositioning is designed. Deploying different number of berthed twice ports in each area, the total costs with corresponding shipping route to find the minimal one are calculated. Case study of Southwest America line shows that when setting one berthed twice port located in North America it can help shipping company to reduce week operating costs by 2.52%. It can be found an optimized overseas liner route by considering empty container repositioning can help shipping companies saving a lot of operating costs.

container; shipping route; empty container; heuristic algorism

2016-06-23；

2016-07-21

国家自然科学基金资助项目(71301101)；上海市科委工程中心能力提升项目(14DZ2280200)

韩晓龙(1980—)，男，上海市人，上海海事大学副教授，博士;E-mail:superhxl@hotmail.com。

李建，韩晓龙.考虑空箱调运的远洋班轮航线优化[J].广西大学学报(自然科学版)，2016，41(5)：1449-1456.

10.13624/j.cnki.issn.1001-7445.2016.1449

U695.22

A

1001-7445(2016)05-1449-08