基于混合代理模型的高速轨道车辆悬挂参数多目标优化

解欢，杨岳，童林军,3，曾威，谢素超

(1.西京学院 机械工程学院, 陕西 西安 710123；2.中南大学 交通运输工程学院, 湖南 长沙 410075；3.江西应用工程职业学院，江西 萍乡 337042)



基于混合代理模型的高速轨道车辆悬挂参数多目标优化

解欢1，杨岳2，童林军2,3，曾威2，谢素超2

(1.西京学院 机械工程学院, 陕西 西安 710123；2.中南大学 交通运输工程学院, 湖南 长沙 410075；3.江西应用工程职业学院，江西 萍乡 337042)

轨道车辆悬挂参数对车辆运行平稳性和稳定性均具有重要影响，对悬挂参数进行多目标优化能够改善车辆的综合动力学性能。选取对车辆运行平稳性与运动稳定性均具有较大影响的悬挂参数为变量参数，构建面向车辆横向Sperling指标、脱轨系数与轮重减载率的Kriging代理模型、二阶RSM(Response Surface Method)模型和RBF(Radial Basis Function)模型。以R2决定系数为拟合精度衡量指标，选择具有最高拟合精度的3类代理模型构成拟合车辆动力学性能指标的混合代理模型。在此基础上，以构建的混合代理模型为目标函数，建立轨道车辆悬挂参数的多目标优化模型。使用NSGA-II算法寻优计算获得悬挂参数的优化值。轨道车辆多体动力学模型仿真计算结果表明：对悬挂参数优化后，车辆的运行平稳性与运动稳定性均得到明显改善。

混合代理模型；Kriging；RBF；RSM；悬挂参数；NSGA-II

轨道车辆的悬挂参数对车辆的运行平稳性、运动稳定性等动力学性能具有重要影响。采用先进的设计方法获得优化的悬挂参数可以提升轨道车辆的动力学性能。为了优化轨道车辆悬挂参数，相关学者通过构建轨道车辆及悬挂系统的动力学理论模型和多目标优化设计模型，采用先进的优化设计方法获得了较优的悬挂参数组合，改善了轨道车辆的动力学性能。周劲松等[1]为了提高轨道车辆的蛇行运动稳定性与曲线通过能力，对车辆的一系横向刚度与一系纵向刚度进行了组合优化，提高了车辆的蛇行稳定性与曲线通过能力。Nejlaoui等[2]考虑一系横向刚度、一系纵向刚度、二系横向刚度、二系纵向刚度、转向架质量、车体质量、等效锥度对车辆运行平稳性与稳定性的影响，通过对悬挂参数进行多目标优化设计，提高了车辆运行平稳性与稳定性。Shieh等[3]采用基于EA(Evolutionary Algorithm)遗传算法的多目标优化算法，对轨道车辆悬挂系统弹簧刚度、阻尼参数进行了优化设计，较大幅度改善了车辆的垂向平稳性。但是，在对车辆悬挂参数进行优化时，构建的车辆动力学模型具有明显的非线性特征，使得悬挂参数多目标优化设计计算复杂，导致悬挂参数优化求解耗时长、优化结果局部最优，不利于快速、准确的获得优化的轨道车辆悬挂参数。代理模型使用由设计参数构建的简单函数替代耗时的理论模型，使得轨道车辆悬挂参数的多目标优化求解效率得到提高。但是，代理模型存在一个重要缺陷，即在拟合不同的问题甚至是同一个问题的不同参数时，不同类型代理模型的精度差别很大，甚至得到错误结果，这限制了代理模型在工程优化中的应用[4]。基于此，Gu 等[5]提出了基于混合代理模型的优化设计方法，通过并行采用多类型代理模型进行计算，搜索获得设计变量对响应值的敏感区域，然后在该区域中重复撒点、缩小搜索区域，直到获得收敛的最优设计值为止。该优化方法能够有效缩小设计变量空间，从而快速获得响应值的最优解。但是，当拟合强非线性问题时，容易导致优化求解结果陷入局部最优。本文基于混合近似模型理论，采用具有不同特性的3类代理模型——Kriging模型、二次多项式响应面模型和径向基函数模型分别建立不同动力学性能指标的3种代理模型，通过拟合精度对比分析，分别选择全局精度最高的代理模型拟合相应的动力学性能指标，构建轨道车辆动力学性能混合代理模型，并以此为目标函数，建立轨道车辆悬挂参数的多目标优化模型，对轨道车辆悬挂参数进行多目标优化设计，获得悬挂参数的全局最优解。

1　3种代理模型基本理论

1.1Kriging模型

Kriging模型是一种估计方差最小的无偏估计模型，能以已知数据样本的动态构造为基础，充分考虑变量在取值范围内的相关特征，通过分析已知数据样本的趋势与动态，较好的拟合响应变量与设计变量之间的非线性问题。Kriging模型包括回归部分和非参数部分[6]：

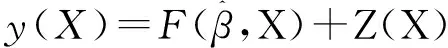
(1)

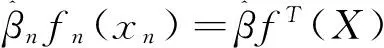
(2)

Z(X)是均值为0，方差为σ2的随机过程，两插值点间的协方差为：

Cov[Z(xi),Z(xj)]=σ2R[R(xi,xj)],

(3)

其中：σ2为随机过程方差；R为n×n阶的对称正定对角矩阵；R(xi,xj)是n个样本点中任意2个采样点xi与xj的空间相关函数，工程应用中通常采用高斯相关函数：

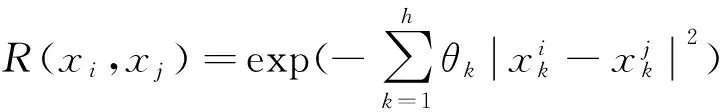
(4)

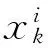
1.2二阶RSM模型

响应面法基于试验设计，使用一个确定的显示函数构建响应参数与变量之间的关系。在一个相对小的区域内，可以使用多项式模型近似反映真实函数关系，从而简化复杂模型。在实际应用过程中，因为3次及其以上的多项式响应面近似模型中存在一个或多个拐点，会干扰预测结果，因此工程应用中多采用二阶多项式响应面模型[7]，其函数表达式为：

(5)

其中，各项系数利用最小二乘法计算得到：

β=(xTx)-1xTy=[β0,β1,…,β20]

(6)

1.3RBF模型

径向基函数代理模型是由一系列使用相同方法构建的函数通过线性加权叠加的方式构建的，其特点是灵活性好、结构简单、计算量较少[8]。径向基函数模型数学表达式为：

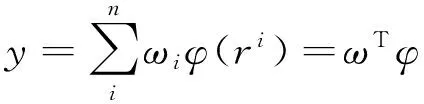
(7)

其中，φ=φ(ri)=φ(‖x-xn‖)T为基函数，不同的基函数获得的预测精度不同；ωi=(ω1,ω1,…,ωn)T为权系数。

2　高速轨道车辆动力学模型

轨道车辆系统中刚体数目较多，在分析过程中为了避免模型振动自由度过多造成的分析困难问题，只考虑车体、前后构架和轮对的点头、摇头、浮沉，侧滚自由度[9]。车辆悬挂系统包括一系悬挂系统和二系悬挂系统，构建得到的轨道车辆多体动力学模型如图1所示。

以某型高速客车车辆为研究对象，确定动力学模型中对应的代号含义以及设计参考值如表1所示。

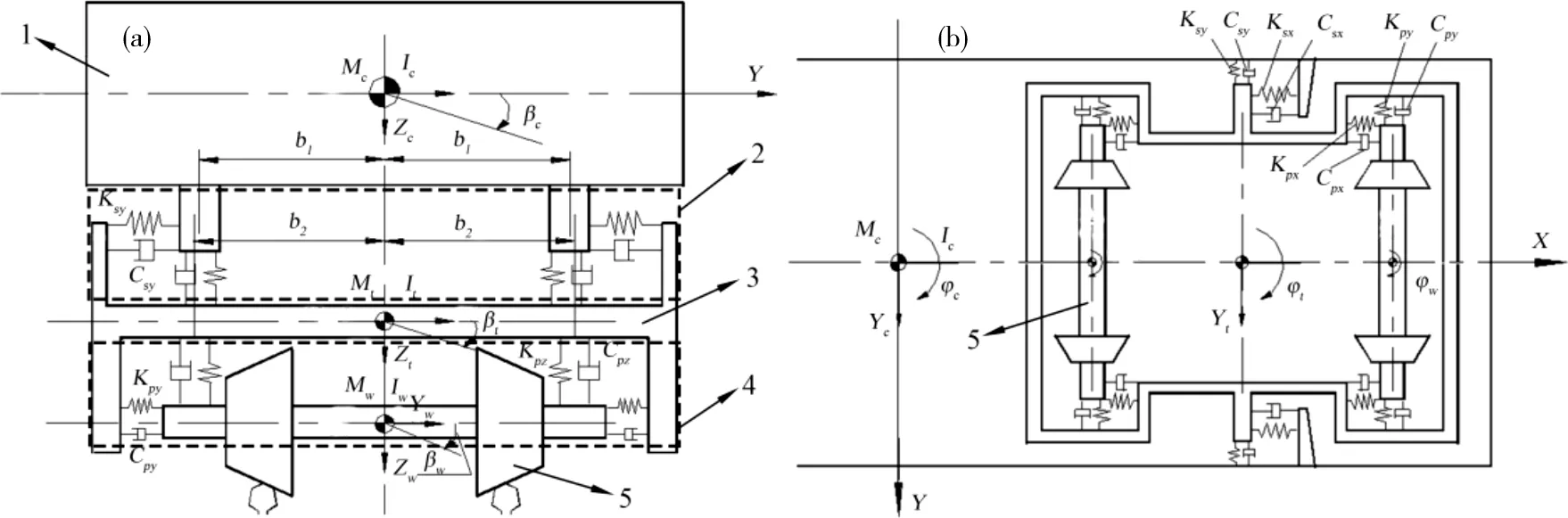
1—车体；2—二系悬挂系统；3—构架；4—一系悬挂系统；5—轮对(a)正视图；(b) 俯视图图1　轨道车辆多体动力学模型Fig.1 Multi-body dynamics model of the rail vehicle

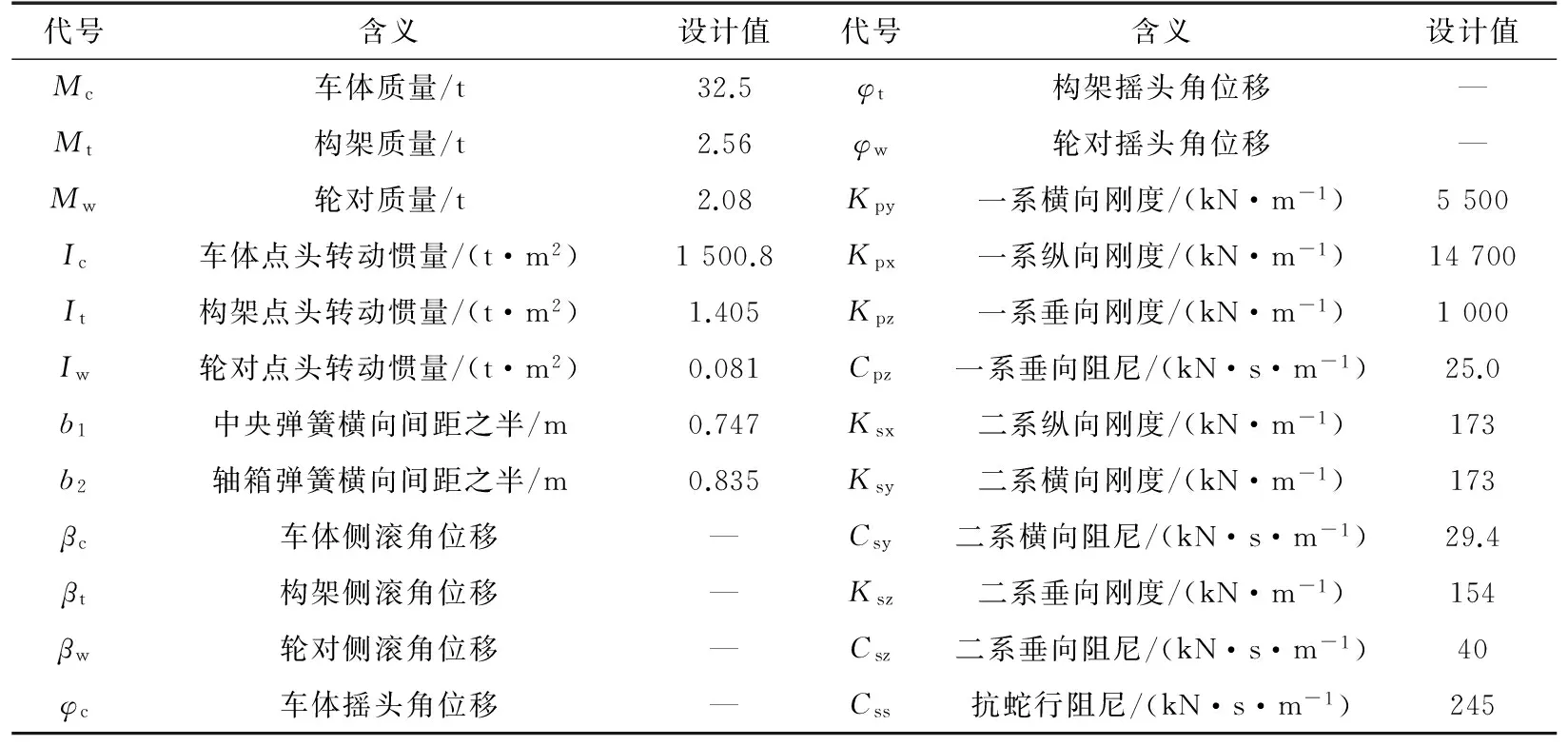
代号含义设计值代号含义设计值Mc车体质量/t32.5φt构架摇头角位移—Mt构架质量/t2.56φw轮对摇头角位移—Mw轮对质量/t2.08Kpy一系横向刚度/(kN·m-1)5500Ic车体点头转动惯量/(t·m2)1500.8Kpx一系纵向刚度/(kN·m-1)14700It构架点头转动惯量/(t·m2)1.405Kpz一系垂向刚度/(kN·m-1)1000Iw轮对点头转动惯量/(t·m2)0.081Cpz一系垂向阻尼/(kN·s·m-1)25.0b1中央弹簧横向间距之半/m0.747Ksx二系纵向刚度/(kN·m-1)173b2轴箱弹簧横向间距之半/m0.835Ksy二系横向刚度/(kN·m-1)173βc车体侧滚角位移—Csy二系横向阻尼/(kN·s·m-1)29.4βt构架侧滚角位移—Ksz二系垂向刚度/(kN·m-1)154βw轮对侧滚角位移—Csz二系垂向阻尼/(kN·s·m-1)40φc车体摇头角位移—Css抗蛇行阻尼/(kN·s·m-1)245

3　高速轨道车辆动力学性能代理模型构建及精度分析

3.1代理模型设计变量的选择

高速轨道车辆的动力学性能主要应用运行平稳性与稳定性指标对之进行衡量。为了构建面向运行平稳性与运动稳定性的代理模型，需首先确定代理模型的设计变量。综合文献[2]，[10]和[11]的研究结果，影响车辆垂向平稳性的悬挂参数主要是二系垂向刚度、二系垂向阻尼、一系垂向刚度、一系垂向阻尼；影响车辆运行横向平稳性的悬挂参数主要是二系横向刚度、二系横向阻尼、一系横向刚度、二系纵向刚度；影响车辆运动稳定性的悬挂参数主要是一系纵向刚度、一系横向刚度、抗蛇行阻尼。其中，一系横向刚度对车辆横向平稳性和运动稳定性两者均具有较为显著的影响。由于对车辆运行平稳性与运动稳定性不存在耦合影响的车辆悬架参数(如二系垂向刚度、二系垂向阻尼、一系垂向刚度、一系垂向阻尼)可单独进行优化，本文的研究重点是通过构建轨道车辆代理模型，对车辆运行平稳性与运动稳定性具有重要影响且存在相互耦合作用的悬架参数进行优化，故在构建车辆代理模型的过程中，选择一系纵向刚度Kpx，一系横向刚度Kpy，二系纵向刚度Ksx，二系横向刚度Ksy，二系横向阻尼Csy和抗蛇行阻尼Css作为代理模型的设计变量。根据设计要求，将各变量参数以初始值为中心，上、下浮动50%作为变量参数的上、下极限，确定变量参数的取值区间如表2所示。

表2　代理模型变量参数取值区间Table 2 Value ranges of the design parameters for surrogate models

根据GB/T 5599—1985[12]，采用Sperling指标对车辆的横向平稳性进行评价，采用脱轨系数和轮重减载率对车辆运动稳定性进行评价。因此，分别以车辆横向Sperling指标HS，脱轨系数QP和轮重减载率JZ作为代理模型的响应参数，构建轨道车辆动力学性能代理模型。

3.2轨道车辆动力学性能Kriging代理模型

为了构建车辆动力学性能Kriging代理模型，需要选择数量至少为3k的训练样本计算高斯相关函数的内部参数θ。其中，k=(n+1)(n+2)/2，n为Kriging模型的变量参数数目[6, 14]。因为本文变量参数数目为6，因此需要的训练样本规模至少为84。为了保证样本的数量，本文将样本规模设置为100。为了确保训练样本抽样的均匀性，使用拉丁超立方试验设计(Latin Hyper-cubic Design, LHD)[13]在表2所示的参数区间中进行抽样。采用如图1所示的轨道车辆动力学模型，计算抽样得到的100组悬挂参数对应的车辆动力学性能指标HS，QP和JZ，构建得到Kriging代理模型的训练样本，如表3所示。

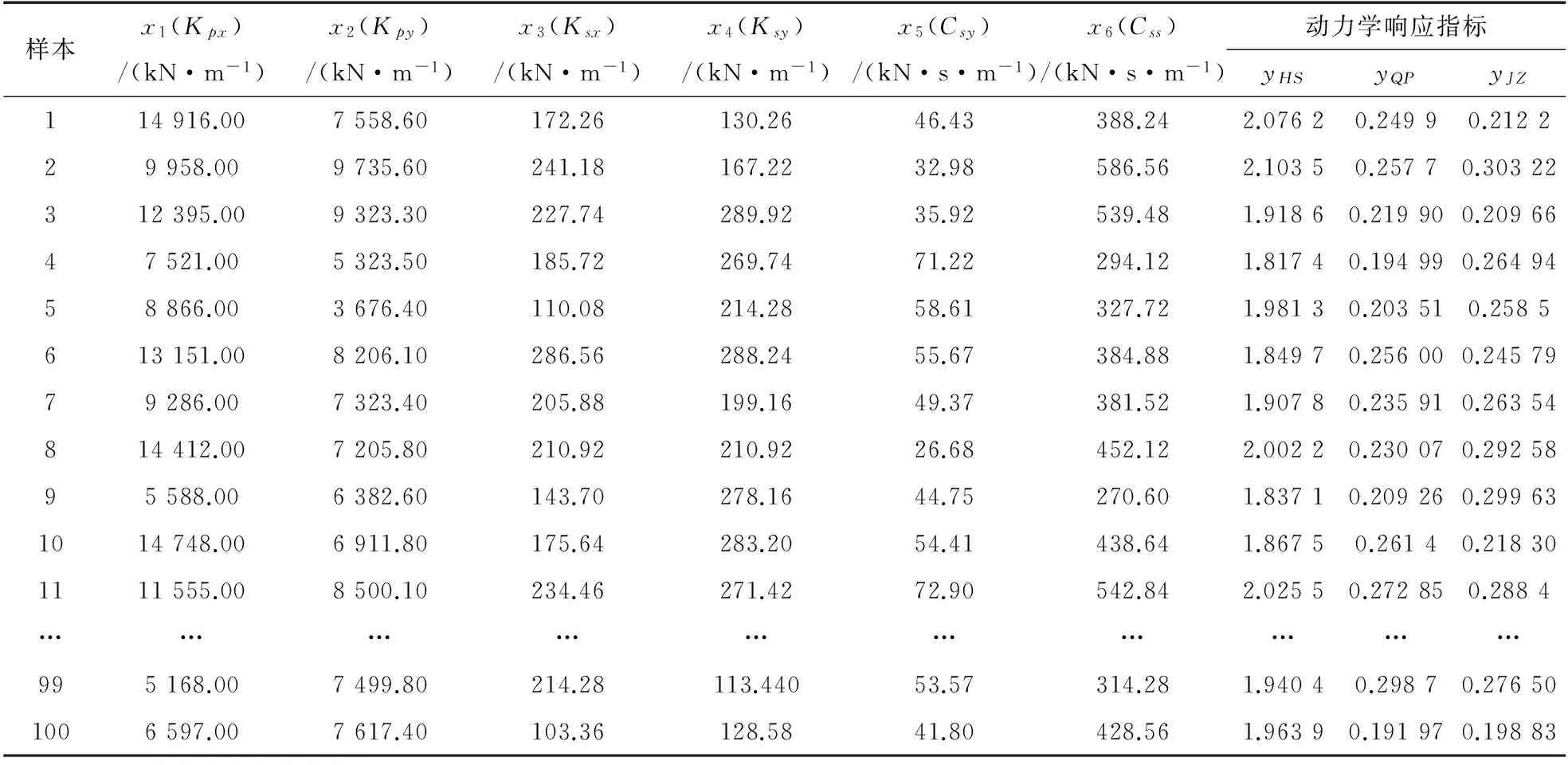
表3　代理模型训练样本Table 3 Training sample of the surrogate models

采用最大似然估计方法[14]，分别计算得到横向Sperling指标Kriging代理模型的相关参数[θk]HS，脱轨系数Kriging代理模型的相关参数[θk]QP和轮重减载率Kriging代理模型的相关参数[θk]JZ为：

[θk]HS=[0.365 90.454 70.066 7

0.137 50.167 21.183 2],

(8)

[θk]QP=[1.204 20.701 00.117 5

0.099 80.075 10.605 9],

(9)

[θk]JZ=[1.425 40.558 20.151 8

0.064 00.348 20.359 8].

(10)

得到相关参数θk后，根据式(4)计算得到未知点x与已知样本数据之间的相关向量，利用式(1)即可构建得到不同动力学性能指标的Kriging代理模型。

3.3轨道车辆动力学性能二次RSM模型

为了构建车辆动力学性能二次RSM代理模型，采以表3所示训练样本，应用最小二乘法确定二次RSM模型的各项系数，最终构建得到的轨道车辆横向Sperling指标HS的RSM代理模型为：

(11)

脱轨系数QP的RSM代理模型为：

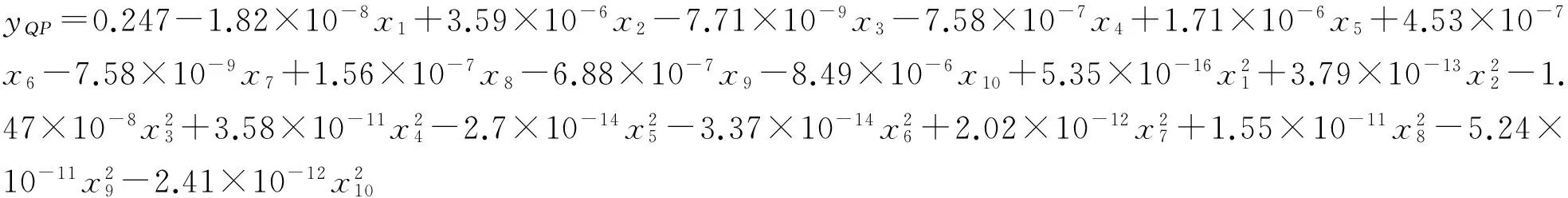
(12)

轮重减载率JZ的RSM代理模型为：

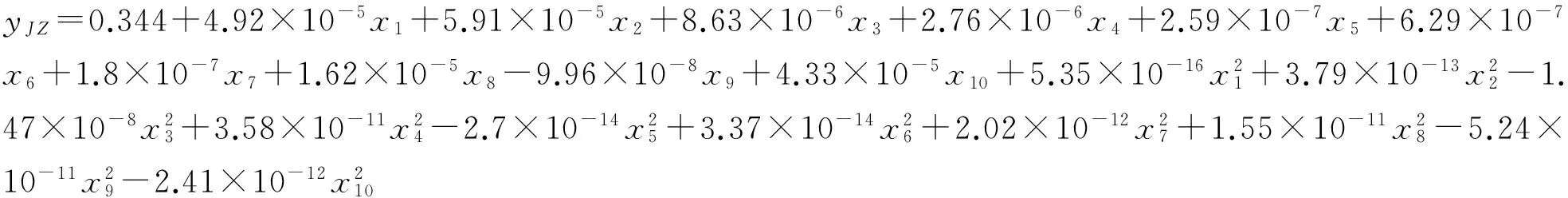
(13)

3.4轨道车辆动力学性能RBF模型

3.53种代理模型精度分析

为了对3种代理模型的预测精度进行分析，采用R2决定系数对各代理模型的预测精度进行对比。R2决定系数的计算方法[7]如式(14)所示：

(14)

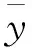
为了检验3种代理模型的预测精度，从表3所示使用动力学模型仿真计算获得的训练样本中随机抽取10组样本点作为标准样本，使用R2决定系数对代理模型的预测精度进行检验，其对比如表4所示。

表43种代理模型的拟合精度对比

Table 4 Comparison of the fitting accuracy for the three kinds of surrogate models

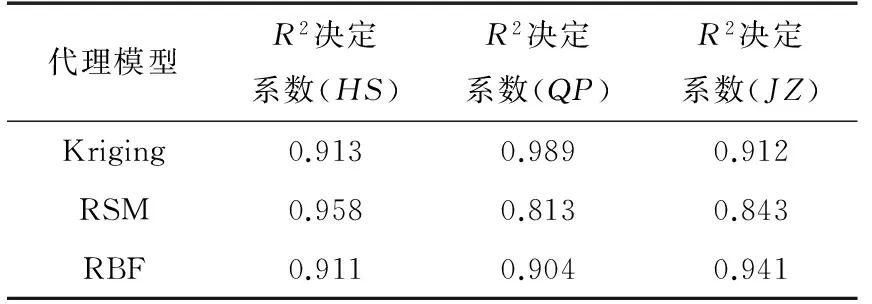
代理模型R2决定系数(HS)R2决定系数(QP)R2决定系数(JZ)Kriging0.9130.9890.912RSM0.9580.8130.843RBF0.9110.9040.941

由表4分析结果可知，在拟合横向Sperling指标HS时，RSM模型的R2决定系数最高，为0.958；在拟合脱轨系数QP时，Kriging模型的R2决定系数最高，为0.989；在拟合轮重减载率JZ时，RBF模型的R2决定系数最高，为0.941。

4　基于混合代理模型的轨道车辆悬挂参数多目标优化

4.1多目标优化模型

由3.5节代理模型的拟合精度对比分析结果可知，RSM模型拟合横向Sperling指标HS的精度最高；Kriging模型拟合脱轨系数QP的精度最高；RBF模型拟合轮重减载率JZ的精度最高。因此，在构建悬挂参数的多目标优化模型时，分别选择RSM模型、Kriging模型和RBF模型构成混合代理模型，并以此作为优化模型的目标函数，以一系纵向刚度Kpx(x1)，一系横向刚度Kpy(x2)，二系纵向刚度Ksx(x3)，二系横向刚度Ksy(x4)，二系横向阻尼Csy(x5)和抗蛇行阻尼Css(x6)为设计变量，构建悬挂参数的多目标优化模型，如式(15)所示。

Find: Kpx,Kpy,Ksx,Ksy,Csy,Css

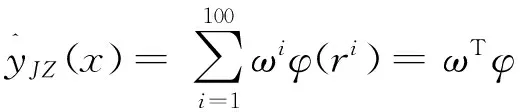
S.t.:yHS≤2.75

yQP≤0.8

yJZ≤0.6

Vcr≥300 km/h

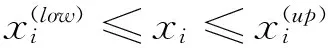
4.2基于NSGA-Ⅱ算法的优化计算

采用第2代非支配排序遗传算法(The second generation of non-dominated sorting genetic algorithm, NSGA-II)[15-16]在变量参数的全局范围内寻优计算，种群规模均为12，进化代数为50，交叉概率为0.9。通过600代进化，其寻优过程如图2所示，获得的Pareto解集如图3所示。

根据多目标寻优计算，获得悬挂参数的最优Pareto解，具体结果为：Kpx=9 663 kN/m，Kpy=5 914 kN/m，Ksx=224.5 kN/m，Ksy=128.6 kN/m，Csy=28.75 kN·s /m，Css=445.80 kN·s /m。

为了进一步验证本文构建的混合代理模型的有效性，使用文献[5]提出的混合代理模型优化方法对本文轨道车辆悬挂参数进行优化，获得对应的悬挂参数优化结果为：Kpx=12 211 kN/m，Kpy=4 925 kN/m，Ksx=153 kN/m，Ksy=218.8 kN/m，Csy=31.55 kN·s/m，Css=345.70 kN·s /m。

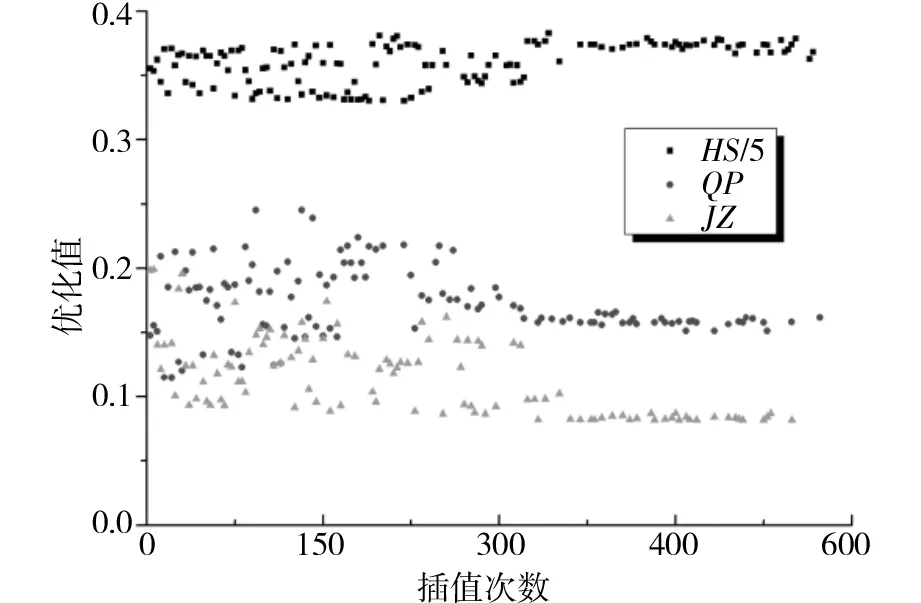
图2　悬挂参数寻优过程Fig.2 Searching process of the optimal suspension parameters

图3　Pareto解集曲面Fig.3 Pareto solution surface

最后，将悬挂参数初始值与使用不同方法获得的优化结果列于表5中。

4.3悬挂参数优化前后的车辆动力学性能对比

为了分析优化前后，以及不同优化方法的优劣，需要计算不同悬挂参数对应的车辆动力学性能指标。因此，将悬挂参数初始值与使用不同方法获得的优化悬挂参数值输入车辆参数化虚拟样机中进行仿真计算，得到如图4(a)所示的优化前后车辆的横向加速度时域图，图4(b)所示的优化前后脱轨系数时域图，图4(c)所示的优化前后轮重减载率时域图。

表5　悬挂参数初始值与优化结果Table 5 Initial and optimized values for suspension parameters

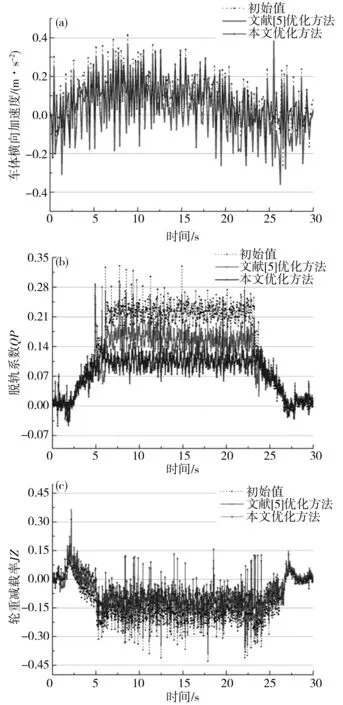
(a)车体横向加速度；(b)脱轨系数(c)轮重减载率图4　悬挂参数优化前、不同优化方法对应车辆动力学性能指标对比Fig.4 Comparison of the dynamics indexes for the rail vehicle in different optimization method

从图4可知，不论采用何种优化方法，优化后车辆的横向加速度变化幅度下降，车辆横向平稳性得到改善，但是本文优化方法获得的悬挂参数对应的动力学性能指标较佳；同时，优化后车辆的脱轨系数与轮重减载率的波动以及最大幅值都降低，车辆的运动稳定性得到提高，且使用本文优化方法优化后车辆的运动稳定性得到明显改善。优化前后车辆动力学性能指标均值对比如表6所示。

表6优化前后车辆动力学性能指标对比

Table 6 Comparison of the dynamics index before and after optimization

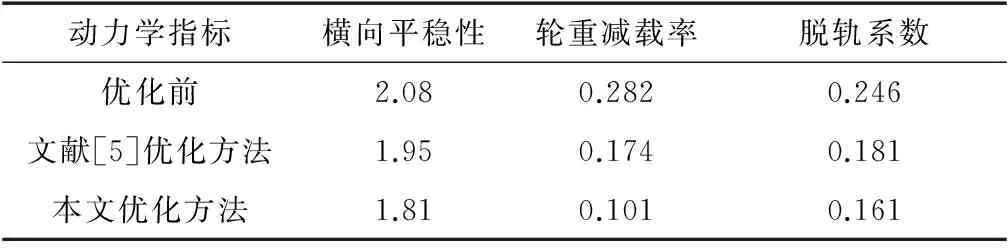
动力学指标横向平稳性轮重减载率脱轨系数优化前2.080.2820.246文献[5]优化方法1.950.1740.181本文优化方法1.810.1010.161

5　结论

1)在构建面向运动稳定性的代理模型过程中，选择一系纵向刚度Kpx，一系横向刚度Kpy，二系横向刚度Ksy，二系纵向刚度Ksx，二系横向阻尼Csy和抗蛇行阻尼Css作为设计变量，分别构建轨道车辆横向Sperling指标HS，脱轨系数QP和轮重减载率JZ为响应参数的Kriging代理模型、二阶RSM模型和RBF模型，为悬挂参数的多目标优化提供了可供选择的高效率目标函数。

2)以R2决定系数作为代理模型拟合精度的衡量指标，对比分析轨道车辆动力学性能指标的各类型代理模型拟合精度，结果表明：二阶RSM模型拟合横向Sperling指标HS的精度最高；Kriging模型拟合脱轨系数QP的精度最高；RBF模型拟合轮重减载率JZ的精度最高。

3)以由横向Sperling指标HS的二阶RSM模型、脱轨系数QP的Kriging模型和轮重减载率JZ的RBF模型构成的混合代理模型为目标函数，构建轨道车辆悬挂参数的多目标优化模型。使用NSGA- II算法寻优计算获得了轨道车辆悬挂参数的最优组合为：Kpx=9 668 kN/m，Kpy=5 914 kN/m，Ksx=224.5 kN/m，Ksy=128.6 kN/m，Csy=28.75 kN·s/m，Css=445.80 kN·s/m。

4)应用轨道车辆多体动力学模型对悬挂参数优化前、不同优化方法优化后对应的车辆的动力学性能指标进行仿真计算，结果表明：优化后车辆的横向加速度、脱轨系数和轮重减载率均明显下降，车辆动力学性能得到优化；与其他优化方法相比，本文方法优化效果更佳，验证了本文方法的有效性。

[1] 周劲松，赵洪伦, 王福天. 铁道车辆稳定性与曲线通过性能折衷最优化研究[J]. 铁道学报, 1998, 20(3): 39-45.

ZHOU Jinsong, ZHAO Honglun, WANG Futian. Study on compromise optimization of stability and curving performance for railway vehicles[J]. Journal of the China Raiway Society, 1998, 20(3): 39-45.

[2] Nejlaoui M, Affi Z, Houidi A, et al. Analytical modeling of rail vehicle safety and comfort in short radius curved tracks[J]. Comptes Rendus Mécanique， 2009, 337(5): 303-311.

[3] Shieh N, Lin C, Lin Y, et al. Optimal design for passive suspension of a light rail vehicle using constrained multiobjective evolutionary search[J]. Journal of Sound and Vibration, 2005, 285(1-2): 407-424.

[4] 王国春，成艾国，顾纪超，等. 基于混合近似模型的汽车正面碰撞耐撞性优化设计[J]. 中国机械工程, 2011(17): 2136-2141.

WANG Guochun, CHEN Aiguo, GU Jichao, et al.Design optimization on crashworthiness of vehicle front impact based on hybrid approximate model[J]. Chinese Journal of Mechanical Engineering, 2011(17): 2136-2141.

[5] Gu J G Y L, Dong Z. Hybrid and adaptive metamodel based global optimization[C]//Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers & Information in Engineering Conference, San Diego, California, USA: 2009.

[6] Zeng Wei, Yang Yue, Xie Huan, et al. CF-Kriging surrogate model based on the combination forecasting method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2015， DOI： 10.1177/0954406215610149.

[7] 隋允康，宇慧平. 响应面方法的改进及其对工程优化的应用[M]. 北京: 科学出版社, 2011: 68.

SUI Yunkang, YU Huiping. The improvement of the response surface method and application in the engineering optimization[M]. Beijing: Science Press, 2011: 68.

[8] Safdari-Vaighani A, Mahzarnia A. The evaluation of compound options based on RBF approximation methods[J]. Engineering Analysis with Boundary Elements, 2015, 58: 112-118.

[9] 廖耘，杨岳，王婷. 铁路客运列车悬架参数稳健性设计[J]. 铁道科学与工程学报, 2011,8(5): 90-95.

LIAO Yun, YANG Yue, WANG Ting. Robust design of suspension parameters for railway passenger train[J]. Journal of Railway Science and Engineering, 2011， 8(5): 90-95.

[10] 杨岳，张晓峰，张兆丰，等. 面向运行平稳性的铁道车辆悬挂参数灵敏度分析[J]. 铁道科学与工程学报, 2014, 11(2): 116-120.

YANG Yue, ZHANG Xiaofeng, ZHANG Zhaofeng, et al. Sensitivity analysis of railway vehicle suspension parameters on riding stability[J]. Journal of Railway Science and Engineering, 2014, 11(2): 116-120.

[11] 王福天. 车辆系统动力学[M]. 1版. 北京: 中国铁道出版社, 1994: 123.

WANG Futian. Vehicle system dynamics[M].1st ed. Beijing: China Railway Publishing House, 1994: 123.

[12] GB/T 5599—1985, 铁道车辆动力学性能评定和试验鉴定规范[S].

GB/T 5599—1985, Railway vehicles-specification for evaluation of the dynamic performance and accreditation test of people’s republic of China[S].

[13] Roshanian J, Ebrahimi M. Latin hypercube sampling applied to reliability-based multidisciplinary design optimization of a launch vehicle[J]. Aerospace Science and Technology, 2013, 28(1): 297-304.

[14] Yang Yue, Zeng Wei, Qiu Wen-sheng, et al. Optimization of the suspension parameters of a rail vehicle based on a virtual prototype Kriging surrogate model[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail and Rapid Transit, 2015， DOI： 10.1177/0954409715617213.

[15] 余廷芳，王林，彭春华. 改进NSGA-Ⅱ算法在锅炉燃烧多目标优化中的应用[J]. 计算机应用研究, 2013(1): 179-182.YU Tingfang, WANG Lin, PENG Chunhua.Improved non-dominated sorting genetic algorithm applied in multi-objective optimization of coal-fired boiler combustion[J]. Application Research of Computers, 2013(1): 179-182.

[16] Bandyopadhyay S, Bhattacharya R. Solving multi-objective parallel machine scheduling problem by a modified NSGA-II [J]. Applied Mathematical Modelling, 2013,37:6718-6729.

Multi-objective optimization of the suspension parameters for high speed rail vehicle based ona hybrid surrogate model

XIE Huan1, YANG Yue2, TONG Linjun2,3, ZENG Wei2，XIE Suchao2

(1. School of Mechanic Engineering, Xijing University, Xi’an 710123, China;2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China;3.Jiangxi Application Engineering Vocational College, Pingxiang 337042, China)

Both the riding quality and traveling stability of the rail vehicle are affected by the suspension parameters, and the comprehensive dynamics performance of the rail vehicle can be improved by the multi-objective optimization of the suspension parameters. The Kriging, second order response surface and RBF surrogate models of the lateral Sperling index, derailment coefficient and reduction ratio of wheel load are constructed. In these models, design variables are regarded as suspension parameters that affect both the riding quality and traveling stability. Three kinds of surrogate models with the highest fitting accuracy on the corresponding dynamics index are selected to establish the hybrid surrogate model based on the coefficients of determination (R2). On this basis, the multi-objective optimization model of suspension parameters is established based on the objective function constructing with hybrid surrogate model. Then, the optimal values of suspension parameters are obtained by using the NSGA-II algorithm. The multi-body dynamics simulation results indicate that both of the riding quality and traveling stability will improve significantly after the optimization of the suspension parameters.

hybrid surrogate model; Kriging; RBF; RSM; suspension parameters; NSGA-II

2015-12-26

西京学院科研基金资助项目(XJ130238)；国家自然科学基金资助项目(51405516)

杨岳(1962-)，男，湖南桃源人，教授，博士，从事轨道交通设备数字化设计与制造研究；E-mail: yangyue@csu.edu.cn

U270.2

A

1672-7029(2016)10-2056-08