任务导向的共同配送合作博弈收益分配策略

彭欣,成耀荣

(中南大学 交通运输工程学院，湖南 长沙 410075)



任务导向的共同配送合作博弈收益分配策略

彭欣,成耀荣

(中南大学 交通运输工程学院，湖南 长沙 410075)

为了解决以任务为导向的共同配送联盟收益分配问题，提出基于纳什讨价还价法的2阶段收益分配策略。首先，联盟在任务开始前对共同配送收益进行第1次分配，引入企业谈判能力系数建立不对称纳什谈判模型；其次，联盟在任务完成后考虑作业绩效水平对收益分配模型进行修正，得到改进的不对称纳什谈判解；然后，采用模糊综合评价法确定模型中的参数；最后，给出算例验证所用方法的有效性和合理性。算例结果表明：基于纳什讨价还价法的2阶段收益分配策略能有效解决任务导向的共同配送收益分配问题，且能提高企业参与联盟的积极性和企业的作业水平。

共同配送；纳什谈判模型；谈判能力系数；作业绩效水平

以配送任务为导向的共同配送联盟是动态发展的，为了确保配送任务的顺利完成，共同配送联盟生命周期中存在一个自愿签订但又有约束力的合作博弈协议。合作博弈协议除了约束了配送企业的行为外，还约定了各个企业最终分配的收益，如果收益分配对某一个成员企业来说存在不公平、不合理，合作关系即面临破裂的风险，因此，合作收益分配成为共同配送合作博弈的关键问题。基于这种背景，本文对共同配送收益分配问题进行研究，寻求一个相对公平合理的收益分配方案。收益分配的合作博弈解有很多，Maschler等[1]提出N个参与者合作的收益分配公式即Shapley解，从定量方面对收益分配问题进行了研究；Sakawa等[2]研究了模糊环境下基于核仁解的利润与成本分配问题；Kimms等[3]用nucleolus解作为几家航空公司的合作博弈收益分配方案，并证明了该博弈的核为非空；李思杰等[4-5]提出用纳什均衡的合作博弈方法来解决供应链的收益分配问题；Lozano等[6]通过实例对比分析多种收益分配方法，包括夏普利值法，核仁解，核心解，t值法，最小最大核法；王旭等[7-8]应用Raiffa解法构建合作收益分配模型，并分别考虑时间风险因子和服务水平对模型进行修正。杨玉红等[9-13]均利用改进的Shapley值法对合作收益进行分配，并考虑了投入、奉献和贡献等因素对收益分配的影响；任小洋等[14-16]分别采用Nash谈判解进行合作收益分配及成本分摊。在收益分配方法中Shapley值法和Nash谈判法在收益分配中用得较多，Shapley值公正、合理且实用性强，但是对于存在n个企业的共同配送联盟来说，应用Shapley值法必须计算的合作联盟情况数目为2n-1个，任务导向的共同配送联盟很难实现；同时，共同配送收益分配比例的确定实际上是各参与者考虑自身和他人收益的基础上讨价还价的过程，Nash 谈判法更为适用；考虑到共同配送联盟以任务为导向，在分配合作收益时应该考虑到任务开始前任务价值和任务完成后绩效水平的影响。基于以上分析，本文建立基于Nash 谈判法的2阶段共同配送收益分配模型。

1　多人协商对策下的Nash讨价还价谈判模型

设共同配送任务由n个企业组成，N={1,2,…,n}为全体集合，联盟总收益为V(N)，ui为企业i的效用函数。谈判破裂点x0={x01,x02,…,x0n}即为保留收益值，如果分配的收益低于此值，企业则会退出联盟单独行动或者加入到其他联盟。设x={x1,x2,…,xn}为收益分配向量，可行分配集表示为：F={(x1,x2,…,xn)|x1≥x01,x2≥x02,…,xn≥x0n}，共同配送收益分配问题则可看成是多人协商对策问题。

纳什认为2人讨价还价解应该满足5条公理：个体理性、联合理性、对称性、无关选择性及线性不变性，上述公理也适用于多人协商的情形。同时，纳什证明了满足上述公理的谈判解有且仅有1个，该解为如下规划的最优解：

(1)

(2)

xi≥x0i,i=1,2,…,n

(3)

以上模型即为多人协商对策下的纳什谈判模型，模型中效用函数ui的构造应该满足：

1)效用函数是关于收益的增函数；2)满足边际效用递减规律；3)谈判起点效用为0。

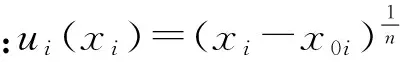
(4)

(5)

xi≥x0i,i=1,2,…,n

(6)

以上非线性规划模型可用matlab编程求解。

2　合作博弈下共同配送收益分配模型

合作开始前，个人理性使得共同配送联盟企业对自身的收益分配值有一定的预期，至少不能低于单独行动获得的收益，集体理性要求所有企业的收益分配值的和不能大于联盟总收益，因此共同配送联盟的收益分配可采取讨价还价问题的纳什解法；任务完成后，每个企业完成的工作有好有坏，联盟对每个企业完成的任务进行绩效评估，根据绩效值高低对初始收益分配值进行改进；因此，本文分2个阶段对共同配送合作收益进行分配。

2.1共同配送收益分配不对称Nash谈判模型

多人协商讨价还价问题的纳什解法是一种简单平均主义解，但在共同配送联盟的实际运作中，由于各成员企业执行的是配送任务中不同的作业环节，在联盟中的地位和运作中所起的作用不同，在共同配送联盟收益分配中的权重也应有所不同。为此，对每个成员企业引入一个谈判能力系数构建不对称Nash谈判模型。

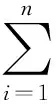
基于以上假设可建立如下考虑谈判系数的共同配送收益分配Nash谈判模型：

(7)

(8)

x0i≤xi≤V(N),i=1,2,…,n

(9)

2.2考虑作业绩效的共同配送收益分配不对称Nash谈判改进模型

共同配送收益分配不对称纳什谈判模型能促进成员企业的合作积极性，但没有考虑任务完成后所有企业完成作业的好坏程度，而任务导向型的共同配送联盟不仅要求配送任务能按客户要求完成，而且还要求较高的客户满意度，从而赢得市场竞争。客户满意度从一定程度上由任务的绩效水平反映，因此，联盟应该对作业绩效水平高的企业给予一定的收益奖励，相反，作业绩效水平低的企业给以相应的收益惩罚。通过作业绩效调节的收益分配值更公平、更合理，在保证了联盟的稳定性的同时为成员企业指明了改进服务的方向。

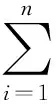
(10)

企业i的作业绩效修正收益为Δxi=V(N)·Δbi，则考虑作业绩效的企业i的收益分配值为：

(11)

3　模型参数分析

3.1各企业愿意接受的收益分配最低值x0i

共同配送联盟中某个成员企业愿意接受的收益分配最低值由企业在执行共同配送任务的过程中所耗费资源的成本及其机会成本共同决定。假设cr表示资源成本，ξ表示行业的平均收益率，收益分配最低值为：

x0i=cr·(1+ξ)

(12)

3.2谈判能力系数ai和绩效水平系数bi

确定谈判能力系数和绩效水平系数的关键在于2个方面：一是建立全面、合理的评价指标体系；二是如何准确地根据评价指标体系计算出谈判能力系数和绩效水平系数。

3.2.1评价指标体系构建

一般来说，成员企业在联盟中的谈判能力通常由企业的综合能力、贡献量、投入量、工作成效等方面反映。以任务为导向的共同配送联盟成员企业的谈判能力系数指企业所完成的配送作业对于整个配送任务的价值，主要包括投入资源价值、配送作业复杂度、配送作业风险性3个指标，因此本文综合上述3个因素建立配送企业谈判能力指标体系，如图1所示。

作业绩效水平包括作业时间指标、作业成本指标、作业质量指标和运作过程指标，可建立如图2所示的配送企业绩效水平指标体系。

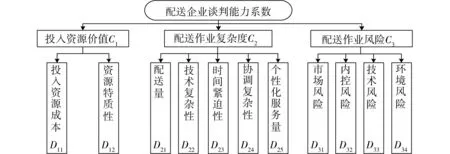
图1　配送企业谈判能力评价指标体系Fig.1 Bargaining ability evaluation index system of distribution enterprise

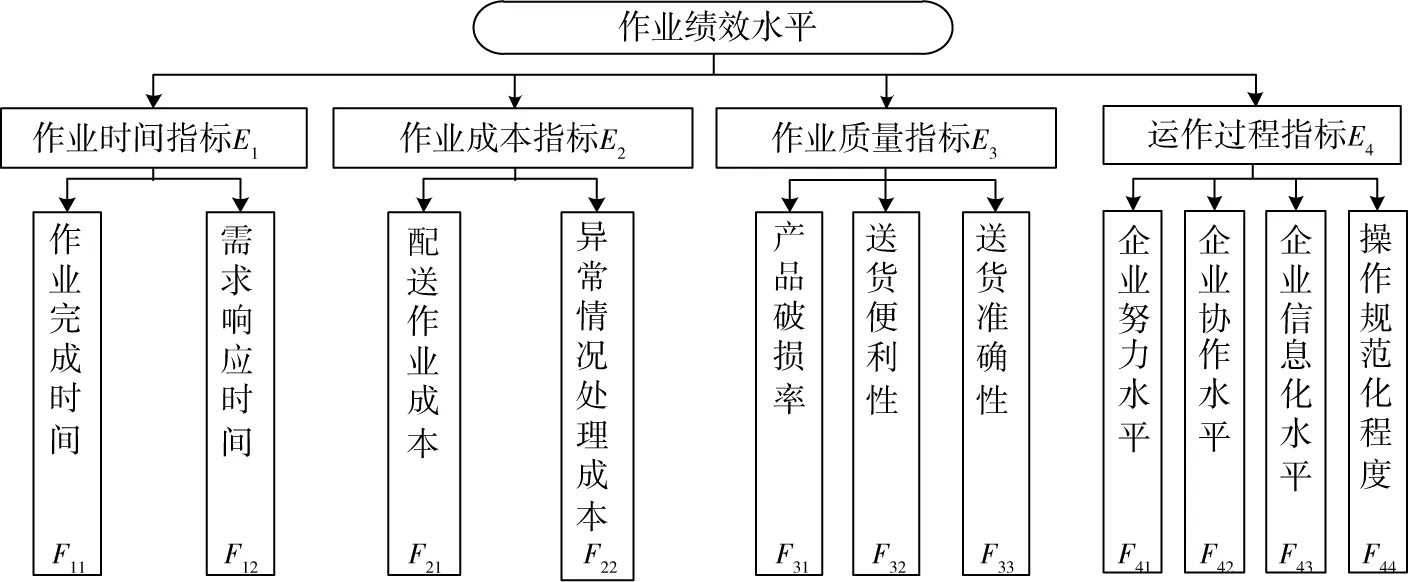
图2　配送企业作业绩效水平评价指标体系Fig.2 Job performance evaluation index system of distribution enterprise

3.2.2基于模糊综合评价法的谈判能力和绩效水平评价模型

谈判能力系数和绩效水平系数的评价主要在于各级指标的权重因子的确定和各级指标的评判值。计算指标权重的方法主要有主观判断法、客观分析法与组合赋权法[17]，为了更科学有效地评价共同配送联盟成员企业的谈判能力系数，避免传统评价方法“主观臆断性”的缺陷，提出三角模糊数与模糊综合评价相结合的评价方法。首先选定如图1～2所示的评价指标体系，其次用三角模糊数原理确定指标权重，最后用模糊综合评价法计算各级指标评价值，具体步骤为：

(13)

其中: l，m和u分别表示模糊数P的下界、中值和上界，u-l越大则模糊程度越高，可信度越低；

2)确定评语集。由专家对同一级指标进行两两比较判断重要性构三角模糊数造判断矩阵：A=

(∂ij)n×n，其中∂ij为指标i和j的相互重要性的三角模糊数。当由多个专家进行判断时，∂ij为多个专家的综合三角模糊数。如果有Y个专家，则综合三角模糊数为：

(14)

表1　判断矩阵标度及其含义Table 1 Judgment matrix scale and its meaning

根据以上评语集综合各个专家的判断值可以得到各个指标的重要性三角模糊数判断矩阵：

(15)

(16)

(17)

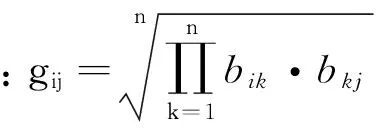
(18)

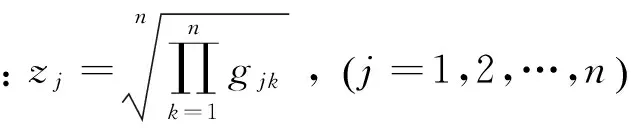
7)模糊综合评价：设配送企业谈判能力和绩效水平的评语集为U=(优、良、中、劣、差)，对应的评判值为L=(1.4,1.2,1.0,0.8,0.6)，则各个因素的模糊评判矩阵为：

(19)

单因素评价矩阵为：Rk=Dk·Fk

(20)

得到准则层模糊关系矩阵为R=(R1,R2,R3)T

(21)

V=C·R=(v1,v2,v3,v4,v5)

(22)

最后计算各个配送企业的谈判能力系数和绩效水平的综合评价值：

ai=V·LTbi=V·LT

(23)

4　算例

某配送联盟承接一个配送订单，由于该配送任务规模较大且任务过程复杂，联盟将配送任务拆分成8个作业分别由8个物流企业执行。已知该联盟的总收益为100 000元，且每个作业的执行企业以及成本如表2所示。

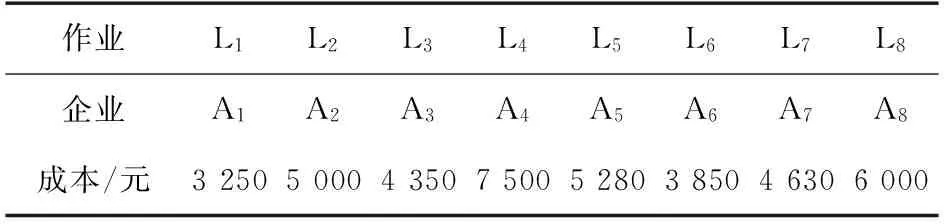
表2　共同配送任务各作业成本Table 2 Job cost of joint distribution task

4.1参数值计算

4.1.1保留收益值x0i计算

假设行业的平均收益率为10%，则每个企业的保留收益分别为：

x0i=(3 575，5 500，4 785，8 250，

5 808，4 235，5 093，6 600)

4.1.2谈判能力系数ai计算

先计算执行第1项作业的企业的谈判能力系数a1，

1)谈判能力评价指标的权重计算

首先计算1级指标层相对于目标层的权重：

由专家团根据表1判断3个指标的相互重要性给出一级指标层的模糊判断矩阵：

A=(∂ij)3×3=

根据式(16)～(18)计算指标权重可得w1=0.317，w2=0.317，w3=0.366。

按照相同的方法计算2级指标相对于1级指标的权重表3所示。

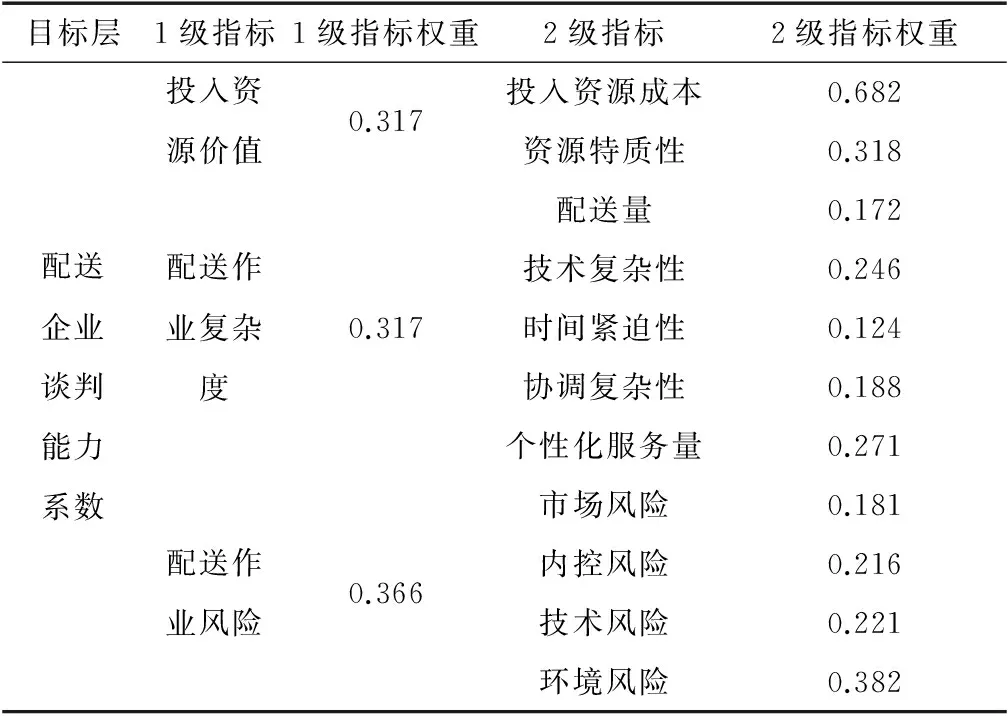
表3　企业谈判能力评价指标权重Table 3 Weight of bargaining ability evaluation index

2)谈判能力综合评价

根据专家团对于配送企业谈判能力单因素指标的等级打分可得每个因素的模糊评判矩阵：

根据式(21)～(24)可计算配送企业的谈判能力系数为：

a1=V·LT=1.071 3

同样算出其他7个企业的谈判能力系数，各个企业的谈判能力系数为：

(1.071 3,1.34,1.732,2.49,1.232,2.875,1.455,1.574)，

规范化得： ai=(0.078,0.097,0.126,0.181,0.089,0.209,0.106,0.114)

4.1.3作业绩效水平bi计算

按照相同的方法根据配送企业作业绩效水平指标体系评价作业绩效水平值，考虑到论文篇幅，不再列出计算步骤，计算得出各个企业的作业绩效水平为：

bi=(0.09,0.17,0.12,0.11,0.15,0.07,0.13,0.14)

4.2确定收益分配值

用matlab软件编程并将上述求得的保留收益、谈判能力系数和作业绩效水平系数代入收益分配模型中可得任务完成前的多人不对称纳什谈判值和任务完成后考虑绩效水平的纳什谈判值，如表4所示。

表4中结果显示：共同配送收益分配的一般纳什谈判解只考虑了企业投入的资源成本，企业4投入的成本额最大因而分配的收益也最多，企业1投入的成本额最小因而分配的收益最少；考虑企业谈判能力系数的纳什解根据谈判能力系数对一般纳什解进行修正，执行的作业价值越高，分配的收益越高，企业4和企业6由于谈判能力系数较大而得到了收益分配值的增加，企业1,2,5和7因为谈判能力系数较小导致收益分配值的减少；任务完成后考虑作业绩效水平的收益分配值则更加公平，企业4作业绩效水平较低导致企业的收益分配值减少，而企业5由于作业绩效水平较高而得到了更高的收益分配值。因此，基于纳什谈判解的2阶段收益分配策略全面考虑了企业执行作业的价值和企业作业绩效水平，使得收益分配更为公平、合理。

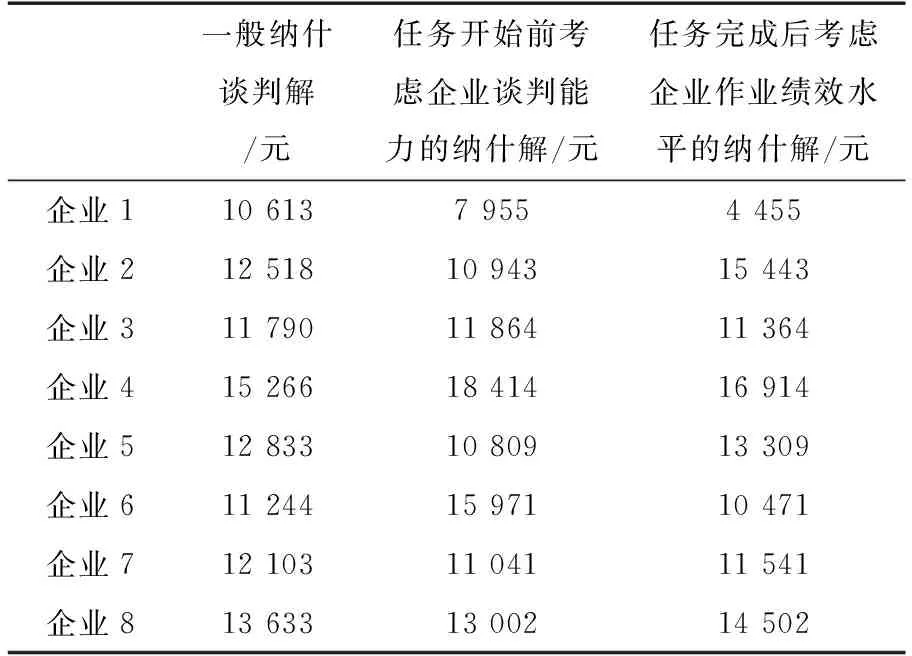
表4　共同配送收益分配纳什谈判值Table 4 Nash value of joint distribution profit allocation

5　结论

1)从合作博弈的角度提出基于纳什谈判模型的2阶段收益分配策略，第1个阶段在不对称纳什谈判模型中引入企业谈判能力系数，考虑了企业所承担配送作业在总体配送任务中的价值；第2个阶段考虑企业的作业绩效水平对第1阶段的收益分配值进行了修正。

2)给出了综合评价企业谈判能力系数和作业绩效水平的评价指标体系，并采用模糊综合评价法确定指标值，避免了传统评价方法“主观臆断性”的缺陷，使得评价更具科学性。

3)通过对模型的求解，可得出基于纳什谈判解的2阶段收益分配策略，全面考虑了企业执行作业的价值和企业作业绩效水平，使得收益分配更为公平、合理，有利于提高企业参与联盟的积极性,同时督促企业不断提高自身的作业水平，为共同配送的稳定发展提供保障。

[1] Maschler M, Peleg B, Shapley L S. Geometric properties of the kernel, nucleolus, and related solution concepts[J]. Mathematics of Operations Research, 1979, 4(4): 303-338.

[2] Sakawa M, Nishizaki I, Uemura Y. Fuzzy programming and profit and cost allocation for a production and transportation problem[J]. European Journal of Operational Research, 2001, 131(1): 1-15.

[3] Kimms A, Çetiner D. Approximate nucleolus-based revenue sharing in airline alliances[J]. European Journal of Operational Research, 2012, 220(2): 510-521.

[4] LI S, ZHU Z, HUANG L. Supply chain coordination and decision making under consignment contract with revenue sharing[J]. International Journal of Production Economics, 2009, 120(1): 88-99.

[5] 陈则辉, 刘诚, 吕品. 随机产出条件下三级供应链收益分配研究[J]. 铁道科学与工程学报, 2015, 12(1):214-220.

CHEN Zehui, LIU Cheng, LÜ Pin. Research on profit distribution of three-level supply chain with stochastic yield[J].Journal of Railway Science and Engineering , 2015, 12(1) :214-220.

[6] Lozano S, Moreno P, Adenso-Díaz B, et al. Cooperative game theory approach to allocating benefits of horizontal cooperation[J]. European Journal of Operational Research, 2013, 229(2): 444-452.

[7] 王旭, 贺美亮, 林云. 应用 Raiffa 解的共同配送成本分摊模型研究[J]. 现代制造工程, 2008 (5): 19-21.

WANG Xu, HE Meiliang, LIN Yun. A cost allocation model of joint distribution based on the Raiffa solution[J]. Modern Manufacturing Engineering,2008(5):19-21.

[8] 刘洪玉, 金玉然. “家电下乡” 中物流网络联盟的利益分配研究[J]. 统计与决策, 2012 (18): 43-46.

LIU Hongyu, JIN Yuran. Profit allocation of logistics network alliance of “Home Appliances to the Countryside”[J]. Statistics and Decision, 2012 (18): 43-46.

[9] 杨玉红. 基于合作博弈的联合采购利益分配方法研究 [D]. 天津: 天津大学, 2010.

YANG YUHong. Benefit allocation method of joint procurement based on cooperative game[D]. Tianjin: Tianjin University,2010.

[10] 胡丽, 张卫国, 叶晓甦. 基于 Shapely修正的 PPP 项目利益分配模型研究[J]. 管理工程学报, 2011, 25(2): 149-154.

HU Li, ZHANG Weiguo,YE Xiaosu. The PPP project profit distribution model based on Shapley correction [J]. Journal of Industrial Engineering and Engineering Management, 2011, 25(2): 149-154.

[11] 陈伟, 张永超, 马一博, 等. 基于 AHP-GEM-Shapley 值法的低碳技术创新联盟利益分配研究[J]. 运筹与管理, 2012, 21(4): 220-226.

CHEN Wei, ZHANG Yongchao, MA Yibo, et al. Benefit allocation of low carbon technology innovation alliance based on AHP-GEM-Shapley [J]. Operations Research and Management Science, 2012, 21 (4) : 220-226.

[12] 雷勋平. 基于改进 Shapley 值的四级供应链利润分配研究[J]. 计算机应用研究, 2012, 29(6): 2141-2144.

LEI Xunping.Profit allocation of four-level supply chain based on the improved shapley value[J]. Application Research of Computers, 2012, 29 (6) : 2141-2144.

[13] 赵晓丽, 乞建勋. 供应链不同合作模式下合作利益分配机制研究[J]. 中国管理科学, 2007, 15(4): 70-76.

ZHAO Xiaoli,QI Jianxun.Cooperation profit distribution mechanism of supply chain under different cooperation modes[J]. Chinese Journal of Management Science, 2007, 15 (4) : 70-76.

[14] 任小洋. 果蔬农产品配送联盟的组建与利益分配研究[D]. 兰州:兰州理工大学, 2014.

REN Xiaoyang. The formation and profit allocation of fruit and vegetables products alliance [D].Lanzhou: Lanzhou University of Technology, 2014.

[15] 肖玉明. 供应链成本分摊的合作博弈分析[J]. 商场现代化, 2007 (8): 143-144.

XIAO Yuming. Cost allocation of the supply chain based on cooperative game[J].Market Modernization, 2007 (8) : 143-144.

[16] 叶飞. 虚拟企业利益分配新方法研究[J]. 工业工程与管理, 2004, 8(6): 44-46.

YE Fei. New method for profit distribution of virtual enterprise[J]. Industrial Engineering and Management, 2004, 8 (6) : 44-46.

[17] 周文梁, 秦进, 邓连波, 等. 城市轨道网络列车运行计划实施效果综合评价[J]. 铁道科学与工程学报, 2014, 11(1): 118-125.

ZHOU Wenliang, QIN Jin, DENG Lianbo, et al. Comprehensive evaluation for the operation performance of train plan on urban rail network[J]. Journal of Railway Science and Engineering , 2014, 11(1): 118-125.

Profit allocation strategy of task-oriented joint distribution based on cooperative game

PENG Xin, CHENG Yaorong

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

In order to solve profit allocation problem of the task oriented joint distribution alliance, a two-stage income allocation strategy based on the Nash bargaining method has been proposed. Firstly, the alliance allocates the income for the first time before the distribution task starts. Since bargaining ability factor of each enterprise is imported, the asymmetric Nash negotiation model is established. Secondly, the profit allocation model is revised considering job performance level of each corporation after the completion of the task, thus the improved asymmetric Nash bargaining model is set up. Then, the Fuzzy Comprehensive Evaluation method is used to determine the parameters in the model. Finally, an example is given to demonstrate the validity and rationality of the method. It is indicated that the two-stage profit allocation strategy based on Nash bargaining method can solve the profit allocation problem of task oriented joint distribution effectively. This strategy can also improve the enthusiasm of enterprises to participate in the league and the operation level of the enterprises.

joint distribution; Nash bargaining method; bargaining ability factor; job performance

2015-12-24

湖南省自然科学基金资助项目(11JJ5051)

成耀荣(1968-)，男，湖南湘潭人,教授，博士，从事大型物流系统诊断优化与共同配送的研究；E-mail: yaorong@csu.edu.cn

F252

A

1672-7029(2016)10-2070-07