典型装备备件消耗规律研究

古平，辛光，刘慎洋，李思，李震

（1.军械工程学院 装备指挥与管理系，石家庄 050003 2.空军勤务学院 航空四站系，江苏 徐州 221000）

装备通用质量特性及寿命评估

典型装备备件消耗规律研究

古平1，辛光1，刘慎洋2，李思1，李震1

（1.军械工程学院 装备指挥与管理系，石家庄 050003 2.空军勤务学院 航空四站系，江苏 徐州 221000）

目的 制订合理的备件保障计划，提高备件保障工作的科学性。方法 通过对某典型装备中正态寿命件和伽马寿命件修理方法的分析，依据更新过程理论以及概率论和数理统计方法，建立典型装备正态寿命件和伽马寿命件的消耗规律数学模型，并举例说明。结果 通过示例，证明了建立的备件消耗规律数学模型具有较好的适用性。结论 依据备件的消耗规律，可以为建制单位实现备件的精确化保障提供理论依据。

典型装备；正态分布；伽马分布；备件消耗

备件消耗是指在一定时间内、一定条件下，使一定数量装备保持规定状态所使用的备件的品种和数量[1]。实践证明，备件消耗对备件的筹措、储存、供应和管理等各个环节都将产生重要的影响[2—6]。在备件消耗预测实际工作中，由于各种不同原因，往往缺乏充足的历史数据，只能获取备件消耗小样本数据。针对小样本数据，一般统计方法难以取得较好的预测效果。国内外学者在备件消耗预测方面进行了深入的研究，并取得了许多成果。目前备件消耗预测常使用的方法主要有指数平滑法、灰色预计法、回归分析法和人工神经网络等[7—10]。运用更新过程理论，从概率的角度研究备件消耗规律的论文并不多见。

某建制单位的装备由不同的寿命分布单元组成，通过对不同的单元进行分析发现，有的单元使用寿命服从正态分布、有的寿命服从伽马分布等[11]。装备中弱耗损型单元、由随机高应力导致故障的单元以及在耗损故障前正常使用的复杂单元，如齿轮箱、汇流环、减速器等机械件，在工作时使用寿命服从正态分布。单位对装备中的正态寿命件主要采取的维修方式为故障后换件修理，定期维修时不更换。使用寿命服从伽马分布的零部件主要采取的维修方式为故障后换件修理，定期维修时必换。为满足装备对正态寿命件和伽马寿命件的换件修理需求，单位需要事先储备一定数量的备件。当正态寿命件和伽马寿命件存储数量过少时，不能够保证装备顺利完成任务；当正态寿命件和伽马寿命件存储数量过多时，会造成部分正态寿命件和伽马寿命件的积压，且存储时间长的正态寿命件可能会减少工作寿命，甚至在存储期间就可能出现损坏的情况。如何掌握正态寿命件和伽马寿命件的消耗规律，预测一定时期内正态寿命件和伽马寿命件的消耗数量，确定合理的正态寿命件和伽马寿命件储备量是文中要解决的关键问题。通过对正态寿命件和伽马寿命件的分析以及问题的抽象，下面给出此类问题的解决方法。

1　正态寿命件消耗模型

设第i个正态寿命件的工作时间为Ti（i=1，2，3…）。第一个正态寿命件从 0时刻开始工作到 T1时刻发生故障后，第二个正态寿命件接替第一个正态寿命件继续工作，产生了第一次更新，同时因第一个正态寿命件的换件修理产生了第一次消耗；第二个正态寿命件故障后，第三个正态寿命件接替第二个正态寿命件继续工作，产生了第二次更新，同时因第二个正态寿命件的换件修理产生了第二次消耗……显然各正态寿命件的工作寿命是独立的，那么到t时刻为止所更换的正态寿命件数量就构成一个更新过程，（0，t]时间内正态寿命件的消耗数量等于正态寿命件的更新次数。依据更新过程理论，（0，t]时间内正态寿命件消耗数量y≥n（n≥1）的概率[12—13]：

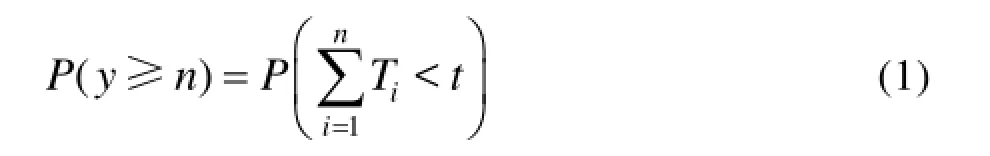
因此，（0，t]时间内正态寿命件消耗量y=（n≥1）的概率为：

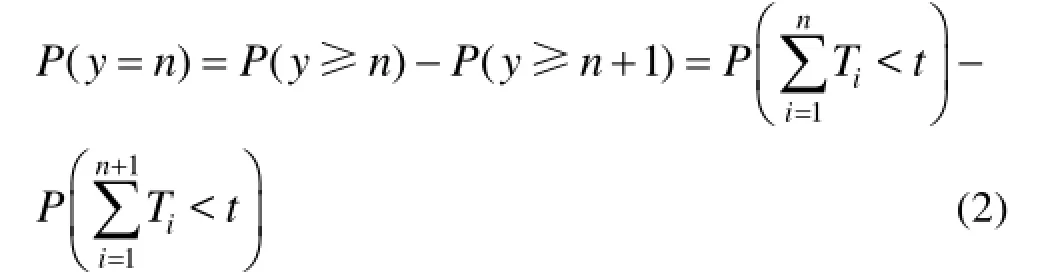
（0，t]时间内正态寿命件消耗量y=0的概率为：

设正态寿命件工作时平均寿命为u，寿命方差为 σ2。则（0，t]时间内正态寿命件的消耗模型的推导过程为：

若 Ti～N（u，σ2）（i=1，2，3，…，n），且它们相互独立，则仍然服从正态分布，且有

依据式（1）—（3），得到（0，t]时间内正态寿命件消耗量y≥n的概率为：

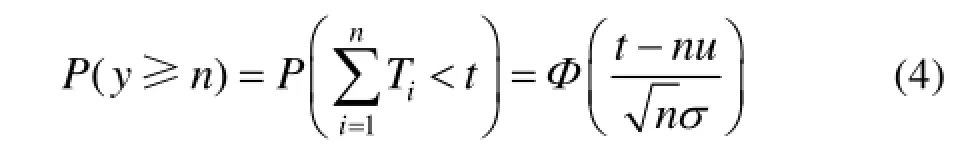
（0，t]时间内正态寿命件消耗量y≥n+1的概率为：

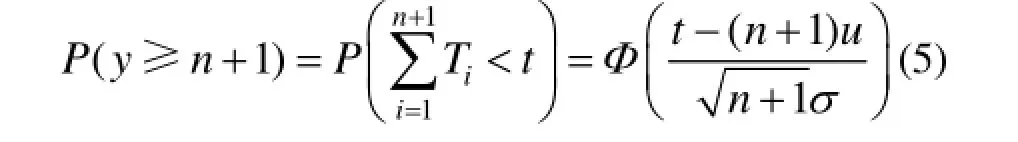
（0，t]时间内正态寿命件消耗量y=0的概率为：

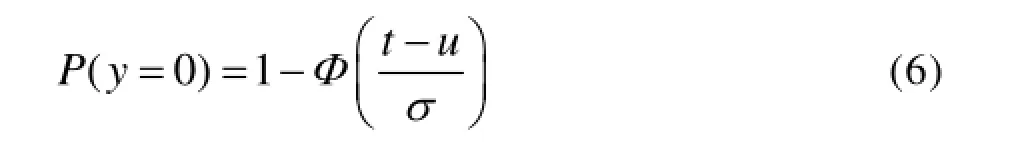
（0，t]时间内正态寿命件消耗量y= n（n≥1）的概率为：

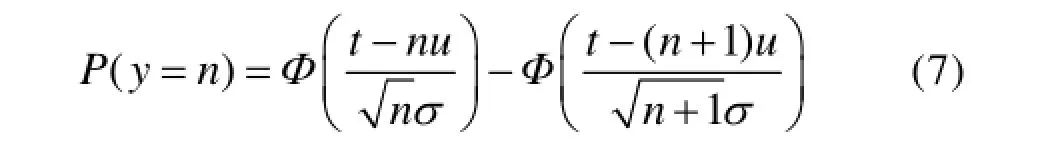
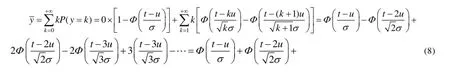
2　伽马寿命件消耗模型

设T为某型号装备的定期维修间隔期，若在装备进行定期小修时，伽马寿命件必须要更换，则T取装备的小修间隔期；若在装备进行定期小修时，伽马寿命件不更换，而在装备进行定期中修时必须要更换，则T取装备的中修间隔期；若在装备进行定期小修和定期中修时，伽马寿命件均不更换，而在装备进行定期大修时必须要更换，则T取装备的大修间隔期。从而得到定期维修时必换的伽马寿命件在[0，T]时间内的消耗量y1=0的概率为：

定期维修时必换的伽马寿命件在[0，T]时间内的消耗量y1=1的概率为：

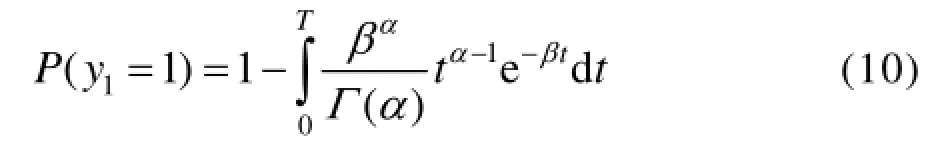
定期维修时必换的伽马寿命件在[0，T]时间内的消耗量y1=k（k =2，3，4…）的概率为[12—13]：

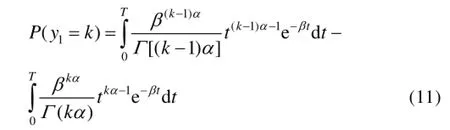
定期维修时必换的伽马寿命件在[0,T]时间内的消耗量平均值为：

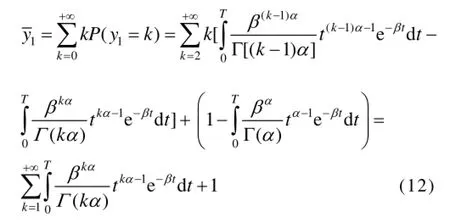
3　应用示例

建制单位使用人员通过对第一种典型装备进行故障数据统计分析和调查，判断出装备在正常工作过程中某部件使用寿命服从正态分布，寿命期u=2×103h，寿命方差σ2=3002h2。当该正态寿命件发生故障后，由本单位的维修人员对该正态寿命件立即实施换件修理，这样能够保证装备始终处于正常的工作状态，定期维修时不对正态寿命件进行更换。试分析该正态寿命件的消耗规律，并预测未来20 000 h内的消耗量。

建制单位使用人员对第二种典型装备进行故障数据统计与分析之后，判断出装备在正常工作过程中某部件使用寿命服从伽马分布，形状参数为α1=6，尺度参数为β1=0.01 /h。该装备从0时刻开始，工作到定期小修的时间间隔为T =3 000 h。装备定期小修时，伽马寿命件采取必换的修理方法。若在装备定期小修之前，伽马寿命件发生故障，为了能够保证装备继续正常工作，立即实施换件修理。试分析伽马寿命件在[0，3000 h]内的消耗规律。

1) 正态分布件消耗规律

依据式（6），得到（0，20 000 h]时间内该正态寿命件的消耗量y=0的概率为：

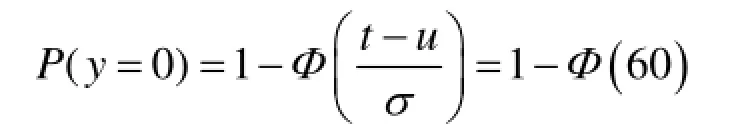
依据式（7），得到（0，20 000 h]时间内该正态寿命件的消耗量y=n（n≥1）的概率为：

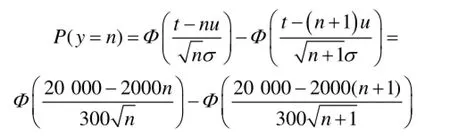
依据式（8），预计未来20 000 h内该正态寿命件的消耗量平均值为：

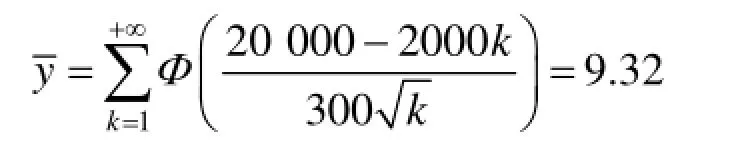
即为满足未来20 000 h内第一种典型装备的保障任务需求，建制单位需要为第一种典型装备平均储备9.32个正态寿命件。

2) 伽马寿命件消耗规律

依据式（9），得到[0，3 000 h]内伽马寿命件的消耗量y1=0的概率为：

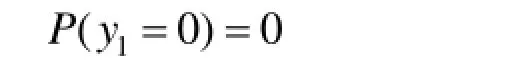
依据式（10），得到[0，3 000 h]内伽马寿命件的消耗量y1=1的概率为：

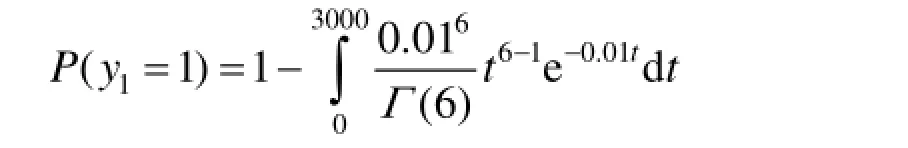
伽马寿命件为必换件，依据式（11），得到[0，

3 000 h]内伽马寿命件的消耗量y1=k（k =2，3，4…）的概率为：

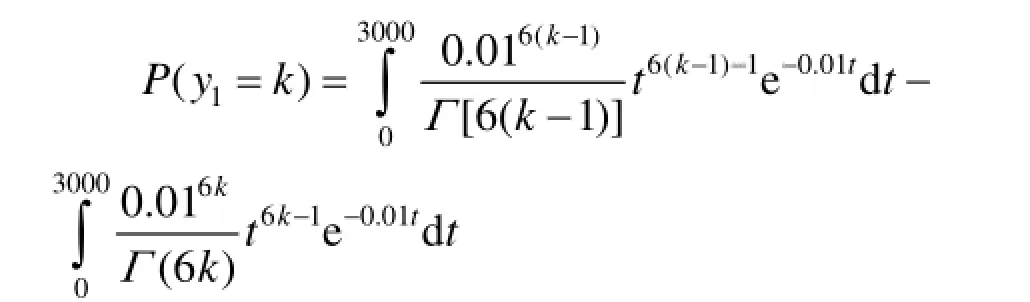
依据式（12），得到伽马寿命件在[0，3 000 h]内的消耗量平均值为：

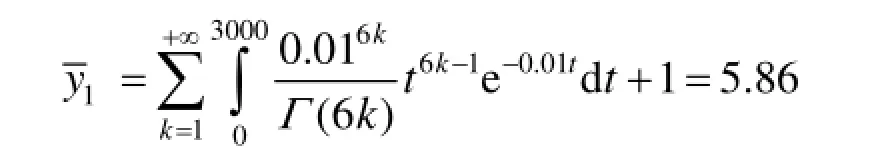
即为满足未来3 000 h内第二种典型装备的保障任务需求，建制单位需要为第二种典型装备平均存储5.86个伽马寿命件。

4　结语

通过对某建制单位装备中正态寿命件和伽马寿命件的分析以及问题的简化，应用随机过程理论、概率论和数理统计方法，推导了正态寿命件和伽马寿命件的消耗规律数学模型，并举例验证了模型的实用性。文中给出的方法对于掌握正态寿命件和伽马寿命件的消耗规律，准确预测未来一定时期内正态寿命件和伽马寿命件的消耗量，确定合理的正态寿命件和伽马寿命件储备量具有十分重要的意义，借鉴此方法仍然可以研究指数寿命件、威布尔寿命件等其他类型寿命件的消耗模型，为科学地实施备件保障奠定理论基础。在没有备件消耗数据的情况下，可以依据单元寿命分布，使用文中建立的消耗规律数学模型预测备件消耗量；在已获取备件消耗数据的情况下，应将单元寿命分布和备件消耗数据结合起来预测备件消耗量，这样能够提高预测精度。

[1] 高崎. 军械维修器材管理学[M]. 北京: 国防工业出版社, 2011. GAO Qi. Management of Qrdnance Maintenance Material[M]. Beijing: National Defence Industry Press, 2011.刘小群, 马士华. 两层次、多品种货物随机存贮模型研究[J]. 华中科技大学学报, 2005, 33(2): 112—115.

[2] LIU Xiao-qun, MA Shi-hua. The Two-hierarchy Stochastic Inventory Model with Multi-varieties[J]. Journal of Huazhong University of Science and Technology, 2005, 33(2): 112—115.

[3] 王亮, 孙绍荣, 吴晓层. 最小化运输与库存费用的两级分销策略分析[J]. 系统工程理论与实践, 2005, 25(10): 33—38. WANG Liang, SUN Shao-rong, WU Xiao-ceng. The Two-hierarchy Stochastic Inventory Model with Multi-varieties[J]. Journal of Huazhong University of Science and Technology, 2005, 25(10): 33—38.

[4] 李玉峰, 许路铁, 陈永康, 等. 某炮弹地面制导装备可修复维修器材保障研究[J]. 装备环境工程, 2014, 11(5): 132—136. LI Yu-feng, XU Lu-tie, CHEN Yong-kang, et al. Research on Repairable Maintenance Equipment Support of Ground Guidance Kits for a Certain Ammunition[J]. Equipment Environmental Engineering, 2014, 11(5): 132—136.

[5] 李玉峰, 许路铁, 陈永康, 等. 某炮弹地面制导装备维修器材平战一体化保障研究[J].装备环境工程, 2014, 11(6): 159—162. LI Yu-feng, XU Lu-tie, CHEN Yong-kang, et al. Research on Peace-War Combined Support of Maintenance Equipment of Ground Guidance Kits for a Certain Ammunition[J]. Equipment Environmental Engineering, 2014, 11(6): 159—162.

[6] 王铁宁, 王洪炜, 曹钰, 等. 器材供应链联合库存管理策略研究[J]. 中国物流与采购, 2009(13): 56—57. WANG Tie-ning, WANG Hong-wei, CAO Yu. Research on Joint Managed Inventory Strategies of Material Supply Chain [J]. China Logistics & Purchasing, 2009(13): 56—57.

[7] DEKKER R, KLEIJN M J, ROOIJ de P J. A Spare Parts Stocking Policy Based on Equipment Criticality[J]. Production Economic, 2014, 56: 69—77.

[8] CHEN Xiao-hui, SHENG Tian-wen, YI Shu-ping. The Ordering Strategy of Spare Parts of Multi-unit System Based on Periodic Preventive Maintenance[J]. Journal of South China University of Technology, 2012, 37: 95—99.

[9] ZHANG M H, XU Q S, MASSART D L. Averaged and Weighted Averaged Partial Least Squares[J]. Analytica Chimica Acta, 2004, 504: 279—289.

[10] RAMADAN Z, HOPKE P K. Application of PLS and Back Propagation Neural Networks for the Estimation of Soil Propert Ies[J]. Chemometrics and Intelligent Laboratory, 2005, 75: 23—30.

[11] 甘茂治, 康建设, 高崎. 军用装备维修工程学[M]. 北京:国防工业出版社, 2005. GAN Mao-zhi, KANG Jian-she, GAO Qi. Military Equipment Maintenance Engineering[M]. Beijing: National Defence Industry Press, 2005.

[12] 张波, 商豪. 应用随机过程[M]. 北京: 中国人民大学出版社, 2009. ZHANG Bo, SHANG Hao. Applied Stochastic Processes [M]. Beijing: Renmin University of China Press, 2009.

[13] KLEBANER F C. 随机分析及应用[M]. 北京: 人民邮电出版社, 2008. KLEBANER F C. Stochastic Analysis and Applications [M]. Beijing: People's Post Press, 2008.

[14] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京:高等教育出版社, 2008. SHENG Zhou, XIE Shi-qian, PAN Cheng-yi. Probability Theory and Mathematical Statistics[M]. Beijing: Higher Education, 2008.

[15] 张德丰. MATLAB概率论与数理统计分析[M]. 北京: 机械工业出版社, 2010. ZHANG Deng-feng. MATLAB Probability Theory and Mathematical Statistics Analysis[M]. Beijing: Engineering Industry, 2010.

Consumption Rules of Spare Parts in Typical Equipment

GU Ping1, XIN Guang1, LIU Shen-yang2, LI Si1, LI Zhen1
（1.Department of Equipment Command and Management, Mechanical Engineering College, Shijiazhuang 050003, China; 2.Department of Aerial Four Stations, Air Force Logistics College, Xuzhou 221000, China）

Objective To formulate a reasonable support plan for spare parts and improve the scientificity of support for spare parts. Methods Through analyzing the maintenance method of spare parts whose life was subject to normal distribution and gamma distribution in some typical equipment, consumption models of spare parts were established according to stochastic processes and probability theory and mathematical statistics. Examples were given. Results Applicability of the models was proven by examples. Conclusion The models provide a theoretical basis for calculating reserves of spare parts scientifically according to consumption pattern.

typical equipment; normal distribution; gamma distribution; spare parts consumption

2016-05-26；Revised：2016-06-28

10.7643/ issn.1672-9242.2016.05.029

TJ089；TB114

A

1672-9242(2016)05-0166-04

2016-05-26；

2016-06-28

国家自然科学基金资助项目（71401173）

Fund：Supported by the National Natural Science Foundation of China（71401173）

古平（1967—），男，博士，副教授，主要研究方向为装备保障理论与应用。

Biography：GU Ping（1967—），Male，Ph. D.，Associate professor，Research focus：equipment support theory and application.