基于状态空间法的大型气候环境实验室热负荷仿真模型

马建军，刘海燕，成竹

（中国飞机强度研究所，西安 710065）

基于状态空间法的大型气候环境实验室热负荷仿真模型

马建军，刘海燕，成竹

（中国飞机强度研究所，西安 710065）

目的 建立可用于大型气候环境实验室初期设计热负荷计算的方法和模型，对实验室的热负荷进行计算，为制冷系统选型提供依据。方法 通过分析实验室的组成结构和热负荷来源，基于状态空间法建立各部分的热负荷计算方法，在Simulink中搭建以制冷量为输入参数的实验室热负荷计算仿真模型，对实验室空载降温过程进行仿真。结果 该仿真模型可以快速对实验室热负荷进行计算，并且可以方便地增减热负荷模块，实验室在降温过程中热负荷达3500 kW以上，地板结构的热负荷占到了总热负荷50%以上。结论 热负荷计算结果可应用于空调系统和制冷系统的设计和选型，以及控制策略的优化。

大型气候环境实验室；热负荷；状态空间法；Simulink

大型气候环境实验室是以飞机和其他大型装备为试验对象，在实验室内模拟飞机或其他装备在地面遭受的诸如高温、低温、湿热、日照、降雨、降雾、冻雨、大风、降雪等自然气候环境[1]，考核飞机及地面保障设备对这些气候环境的适应性，为飞机等大型装备的环境适应性设计提供参考。大型气候实验室热负荷计算是制冷/加热系统、空气处理系统设计的出发点，决定了实验室温度指标能否实现、系统设计、投资和运行成本，因此准确地计算热负荷非常重要[2—3]。大型气候环境实验室空间巨大、结构复杂、热负荷源项多，若以稳态或假设空气温度线性变化作为边界条件进行热负荷计算，将带来很大误差，因此需进行合理的瞬态热负荷计算。现有的计算方法如有限差分法[4—5]，编程复杂、适应性较差；CFD流固耦合计算[6—8]则耗时过长。状态空间法[9]简化了许多不必要考虑的环节，计算简便，可在 Simulink中快速搭建模型，得到较准确的总的制冷量需求，并可验证控制策略等。对于大型气候环境实验室，可建立基于状态空间法，并联合CFD仿真的热负荷计算方法。利用CFD仿真计算稳态时，不同气流组织下围护结构及试件表面的对流换热系数[10]，将对流换热系数作为状态空间的输入参数进行动态仿真，确定不同工况下的总热负荷，以此设计制冷系统。

1　大型气候环境实验室组成结构

大型气候实验室为“房中房”结构，外层为钢结构建筑，内层为环境室，如图1所示。其有效容积超过105m3。环境室侧墙及天花板均由200 mm厚的聚胺脂保温板拼接而成，地面结构由上到下分为三层：300 mm加强混凝土、300 mm泡沫玻璃、300 mm加强混凝土。

图1 大型气候实验室Fig.1 Large climatic environmental test laboratory

实验室采用的是间接制冷的方式[11]，制冷系统产生的冷量通过载冷剂系统输送到空气处理系统对空气进行冷却。空气处理系统包括新风系统和循环风系统[12]，如图2所示。其中新风系统将室外新风最低处理至-25 ℃，然后送入循环风系统与室内回风混合并进一步降温，实验室内所有的热负荷将通过循环风系统的空气换热器除去。因此，实验室空气处理系统、载冷剂系统、制冷系统应将该热负荷作为设计输入参数。

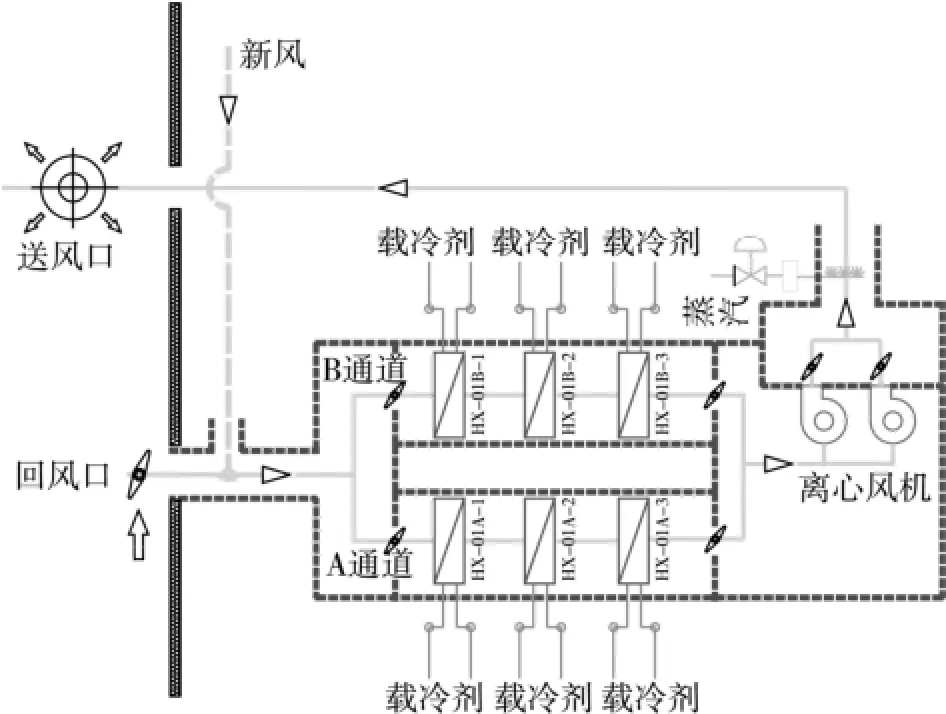
图2 空气处理系统Fig.2 Air handling system

2　建立热负荷仿真模型

大型气候环境实验室的热负荷主要来源为室内空气、保温围护结构、混凝土地面结构、新风、内部钢结构、照明灯、循环风机、试验件等。由于试验件多种多样，难以建立通用的计算模型，暂不考虑，下面建立各个部分的热负荷计算模型。

2.1 室内空气降温放热

室内空气温度的变化是引起保温围护结构、地面结构等温度变化的直接原因，同时结构温度变化产生热负荷反过来影响室内空气温度的变化。同时新风系统持续不断地补充新风以保持实验室压力，在每个时刻室内的空气质量均不同，空气的温度变化按式（1）计算。

式中：Ta为空气温度，K；Q为制冷量，W；q为围护结构、地面结构等的热负荷，W；Va为实验室内部净体积，m3。

2.2 保温围护结构对流传热

保温围护结构主要为聚胺脂夹心板，将保温板分成n层，如图3所示。

图3 保温板分层Fig.3 Layering of insulation panel

取n+1个点温度作为变量，建立n+1维状态变量，空气温度当作输入变量，根据固体传热方程建立常微分方程组[13]。

式中：ci为单位比热容，ci=δiρicpi；δi为节点i与节点i+1之间的厚度，m；ρi为密度，kg/m3；cpi为定压比热，J/(kg·K)；Ri为热阻，Ri=λiδi；λi为导热系数，W/(m·K)；Ta，ha分别为室内温度及表面对流换热系数，K，W/(m2·K)；Tb，hb分别为室外温度及表面对流换热系数，K，W/(m2·K)。

将式（2）改写成：

其中A1是(n+1)×(n+1)维的矩阵。

B1是(n+1)×2的矩阵：

u1是2×1维的输入列向量：

保温板向空气传递的热负荷为：

式中：a1为保温板的面积。

将式（7）写成如下形式：

式中：Y=[q1]，C1=[a1ha0…0]，D1= [-a1ha0]。

式（3）和式（8）共同组成了保温板的状态空间[14]。表面对流换热系数可通过查相关设计手册、实测或CFD分析获得。

2.3 地面结构对流传热

同聚胺脂保温板一样，将地面结构分层，如图4所示。上层混凝土分成w层，中层泡沫玻璃分成k层，底层混凝土分成n层。取（w+k+n+1)个点温度作为状态变量，根据固体导热微分方程建立地面结构的状态方程。

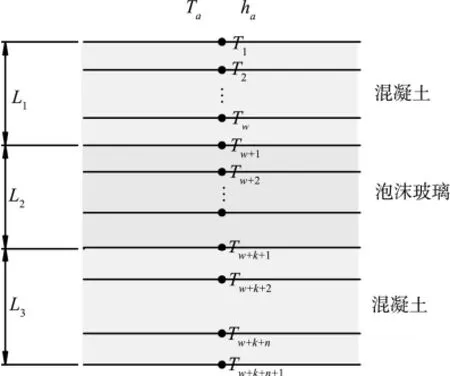
图4 地面结构分层Fig.4 Layering of floor structure

与保温板不同的是，底层混凝土下面是土壤结构，内部有通风管，可以认为其温度是不变的，节点（w+k+n+1)温度微分方程为：

地面向空气传递的热负荷为：

式中：a2为地面结构的表面积。

构建地面结构的传热状态空间为：

其中T为(w+k+n+1)维列向量：

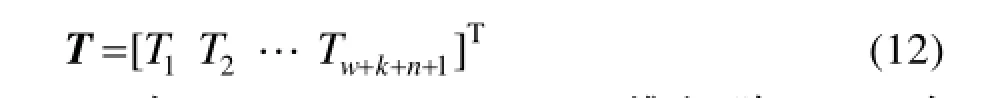
A2为(w+k+n+1)×(w+k+n+1)维矩阵，B2为(w+k+n+1)×1维矩阵，C2为(w+k+n+1)×1维矩阵，D2为(w+k+n+1)×1维矩阵，Y=q3。

2.4 新风降温放热

降温过程中，空气密度变小将导致室内形成负压，造成室外气体渗入，损坏保温结构。因此需持续不断地为实验室补充新风，维持室内保持正压。这是利用一套新风系统实现的，新风系统以质量流量fm˙补充温度最低至-25 ℃的新风进入循环风风道，然后在循环风处理机组内进一步降温。新风的热负荷由式（13）计算。

式中：ta为实验室内空气温度，℃；tf为新风温度，℃。

2.5 循环风机做功产热

循环风机对空气的做功为：

式中：P为风机全压，Pa；V˙为空气流量，m3/s。

在不同的温度下，空气的密度不同，风机的全压按式（15）修正。

式中：P0为标准工况时风机全压，Pa；B为当地大气压力，Pa；t0为设计工作温度，℃；t为工作空气温度，℃。

2.6 照明灯产热

实验室内的照明灯功率恒为q5。

2.7 内部钢结构降温放热

内部钢结构为实验室顶部的承力钢架，其完全处理空气对流当中，相对表面积较大，因此可假设其温度变化率与空气一致，钢结构的质量为msteel，其向室内空气传热量为：

2.8 仿真模型搭建

在MATLAB中编写并计算保温板和地面结构状态空间系数矩阵，在 Simulink[15]中，依据图 5所示的系统原理，搭建各个部件的仿真模块，最终完成输入参数为制冷量的实验室热负荷计算仿真模型，此处记为模型一。

图5 模型一 输入参数为制冷量的热负荷仿真模型Fig.5 Model 1: Thermal load calculation model with cooling capacity as input

3　应用及结果分析

实验室要求24 h内从常温降至-55 ℃，降温速度不大于 3 ℃/min。初步确定新风流量为 24.6 kg/s，循环空气流量为300 m3/s，风机标准环境下总压为1800 Pa，经CFD气流组织仿真得到地面对流换热系数为 15 W/(m2·K)，保温结构表面为 10 W/(m2·K)。照明功率为40 kW，内部钢结构质量为140 t。

假设制冷量随室内空气温度变化呈线性变化，初始温度+35 ℃时制冷量为4000 kW，-55 ℃时制冷量减少至3000 kW。降温过程中各个部分的热负荷见图6，地面结构和空气温度见图7，保温板结构温度见图8。

从图 6—8中可以看出，24 h空气温度降至-55 ℃。空气降温速率先快后慢，4 h左右后温度降至-25 ℃，对应的热负荷迅速降低。地面结构热负荷先升后降，最高达2200 kW，降温结束时仍达1500 kW，占总热负荷的接近 1/2。地面结构的上层混凝土被冻透，中层泡沫玻璃保温性能良好，其底面温度几乎未发生改变。保温板表层是0.8 mm的不锈钢，传热性能良好，因此其表层温度与空气温度几乎保持一致，且保温板保温性能良好，最外层温度仅有略微下降。

图6 模型一 各模块热负荷曲线Fig.6 Model 1: Thermal load of different module

图7　模型一 地面结构不同深度温度曲线Fig.7 Model 1: Temperature of floor structure in different depth

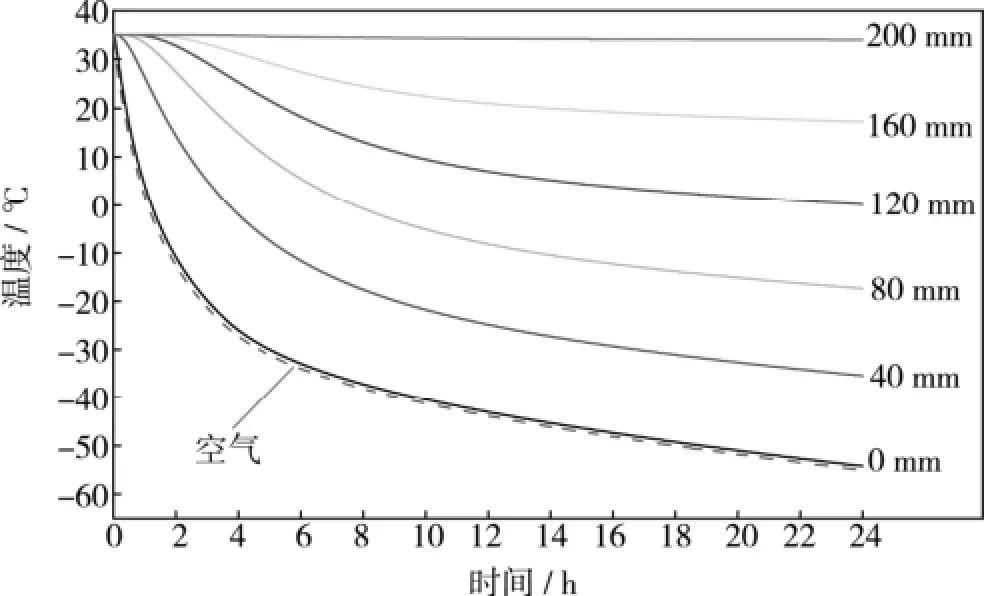
图8 模型一 保温板不同深度温度曲线Fig.8 Model 1: Temperature of insulation panel in different depth

将图5所示的原理将模型稍做调整，就可变为常用的以室内空气温度曲线为输入参数的热负荷计算模型，记为模型二。

图9 模型二 输入参数为室内空气温度曲线的热负荷仿真模型Fig.9 Model 2: Thermal load calculation model with air temperature in door as input

通常假设降温过程中空气温度线性变化：空气初始温度为+35 ℃，经24 h线性降至-55 ℃。降温过程中各模块的热负荷见图 10，地面结构温度见图11，保温板温度曲线见图12。

图10 模型二 各模块热负荷曲线Fig.10 Model 2: Thermal load of different module

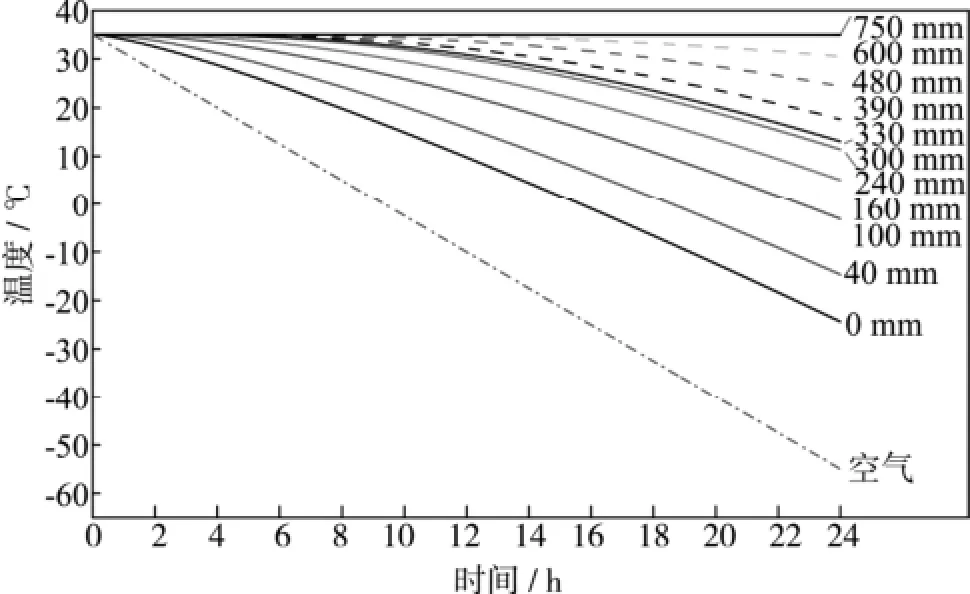
图11 模型二 地面结构不同深度温度曲线Fig.11 Model 2: Temperature of floor structure in different depth

图12 模型二 保温板不同深度温度曲线Fig.12 Model 2: Temperature of insulation panel in different depth

从图10—12中可以看出，总热负荷和各分项热负荷均是逐渐递增的。总热负荷从750 kW逐渐递增至3800 kW，地板结构热负荷从初始的0 kW增至2000 kW，超过总热负荷1/2。两种计算模型的结果对比见表1。

表1 两种模型计算结果对比Table 1 Results of the two thermal load calculation models

制冷系统温度越低，其COP值越低，若以模型二的计算结果作为制冷系统的设计输入参数，将造成机组选型偏大，增大初投资和运行成本。同时降温结束后，模型一得到的地表温度为-33 ℃，比模型二的-24 ℃低，这将更有利于试验区的空气温度均匀性。

4　结语

文中采用状态空间法建立的，以制冷量为输入参数的大型气候环境实验室热负荷仿真模型可以快速、准确地计算瞬态热负荷，模块化的设计使模型容易搭建和修改，且可以很容易调整为以空气温度曲线为输入参数的热负荷仿真模型。降温过程若假设空气温度线性变化，计算得到的热负荷在低温段偏大，以此为设计参数将导致制冷系统选型偏大，同时地表温度降低缓慢，不利于试验区的空气温度均匀性。

实验室建造中，将在地板结构、保温板结构等中预埋温度传感器，根据实测结果对仿真模型进行修正，使仿真结果更精确。可根据具体试验工况编写相应的热负荷模型，如降雪、吹风、太阳辐照等，实时预测热负荷，为制冷系统运行和控制系统控制策略优化提供参数。

[1] 唐虎, 李喜明. 飞机气候试验[J]. 装备环境工程, 2012, 9(1): 60—65. TANG Hu, LI Xi-ming. Climatic Test of Aircraft[J]. Equipment Environment Engineering, 2012, 9(1): 60—65.

[2] 王浚, 黄本诚, 万才大, 等. 环境模拟技术[M]. 北京:国防工业出版社, 1996. WANG Jun, HUANG Ben-cheng, WAND Cai-da, et al. Environment Simulation Technology[M]. Beijing: National Defense Industry Press, 1996.

[3] 李兆坚. 大型综合气候环境室空调制冷设计[J]. 暖通空调, 1999, 29(5): 57—59. LI Zhao-jian. Air Conditioning and Refrigeration Design of a Large Multi-purpose Environmental Test Chamber[J]. HV&AC, 1999, 29(5): 57—59.

[4] 李兆坚. 环境实验室围护结构不稳定传热特性分析[J].环境技术,1992(2): 22—44. LI Zhao-jian. Transit Heat Transfer Analysis of Climatic Test Chamber Insulation Layer[J]. Environmental Techonlogy, 1992(2): 22—24.

[5] 吴志勇. 环境试验箱围护结构传热研究[J]. 装备环境工程, 2007, 4(5): 51—56. WU Zhi-yong. Study on Heat Transfer of Exterior Pretected Construction of Environmental Test Chamber[J]. Equipment Environmental Engineering, 2007, 4(5): 51—56.

[6] 王怡, 刘国华, 陈靖. 建筑室内环境数值模拟中的耦合方法[J]. 建筑科学与工程学报, 2006, 23(4): 79—83. WANG Yi, LIU Guo-hua, CHEN Jing. Coupling Method by Numerical Simulation of Building Indoor Environment [J]. Journal of Architecture and Civil Engineering, 2006, 23(4): 79—83.

[7] ZHAI Zhi-qiang, CHEN Qing-yan, et al. On Approaches to Couple Energy Simulation and Computational Fluid Dynamics Programs[J]. Building and Environment, 2002 (37): 857—864.

[8] 刘海燕, 马建军. 环境实验室气流组织与围护结构耦合传热研究[J]. 装备环境工程, 2016, 13(2): 44—51. LIU Han-yan, MA Jian-jun. Coupled Heat Transfer Analysis of Airflow and Enclosure Structures of Environment Test Chamber[J]. Equipment Environmental Engineering, 2016, 13(2): 44—51.

[9] 翟唤春, 尚娜, 王浚. 环境试验设备的状态空间法仿真设计[J]. 北京航空航天大学学报, 2004, 30(2): 109—113.ZHAI Huan-chun, SHANG Na, WANG Jun. Simulation Desing Based on State-space for Environment Test Equipment[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(2): 109—113.

[10] ZHAI Zhi-qiang, CHEN Qing-yan. Numerical Determination and Treatment of Convective Heat Transfer Coefficient in the Coupled Building Energy and CFD Simulation[J]. Building and Environment, 2004 (39): 1001—1009.

[11] 张惠, 刘海燕, 李喜明, 等. 大型气候环境实验室冷媒的分析选择[J]. 装备环境工程, 2015, 12(2): 104—109. ZHANG Hui, LIU Hai-yan, LI Xi-ming, et al. Analysis and Selection of Refrigerants Used In the Large Climatic Environment Test Facility[J]. Equipment Environmental Engineering, 2015, 12(2): 104—109.

[12] 刘海燕, 马建军, 张惠. 大型气候环境实验室空气处理系统方案讨论[J]. 装备环境工程, 2014, 11(5): 107—113. LIU Hai-yan, MA jian-jun, ZHANG Hui. Discussionon Design of the Air Handing System in Large Climatic Environ-mentalTestLaboratory[J]. Equipment Environment Engineering, 2014, 11(5): 107—113.

[13] 陶文铨. 数值传热学[M]. 第二版. 西安: 西安交通大学出版社, 2001. TAO Wen-quan. Numerical Heat Transfer[M]. 2nd Edition. Xi’an: Xi’an Jiaotong University Press, 2001.

[14] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2013: 419—511. HU Shou-song. Principle of automatic control[M]. Beijing: Science Press, 2013: 419—511.

[15] 王正林, 郭阳宽. MATLAB/SIMULINK与过程控制系统仿真[M]. 北京: 电子工业出版社, 2012. WANG Zheng-lin, GUO Yang-kuan. MATLAB/ SIMULINK and Simulation of Process Control System [M]. Beijing: Electronic Industry Press, 2012.

A Climatic Test Laboratory Cooling Capacity Calculation Model Based on Space State Method

MA Jian-jun, LIU Hai-yan, CHENG Zhu
(Aircraft Strength Research Institute of China, Xi’an 710065, China)

Objective To establish a thermal-load calculation model applied in large climatic test laboratory, the calculation result will help the design of cooling system. Methods First, every potential thermal source was analyzed. Then thermal calculation method and simulation module for thermal source was founded in Simulink. At last a thermal-load simulation models of cooling capacity dominant was set up and applied in the thermal calculation of chamber cooling process. Results The thermal load calculation models is time efficiency for thermal calculation of large climatic test laboratory and convenient in modules update. Thermal load of large climatic test laboratory during cooling down is larger than 3500 kW, thermal load of the floor is more than 50% of the total thermal load. Conclusion The calculation result will help the design of air-condition system and cooling system, and the optimization of control strategy.

large climatic test laboratory; thermal load; state-space; Simulink

2016-09-28；Revised：2016-09-29

10.7643/ issn.1672-9242.2016.05.019

TJ01

A

1672-9242(2016)05-0115-07

2016-09-28；

2016-09-29

中国航空工业集团公司技术创新基金（2013F62302）

Fund：Technology Innovation Fund of Aviation Industry Corporation of China（2013F62302）

马建军（1989—），男，安徽阜阳人，硕士，工程师，主要研究方向为飞机气候环境试验技术。

Biography：MA Jian-jun（1989—）， Male， from Fuyang， Anhui， Master， Engineer， Research focus: aircraft climatic environmental test technology.