分子流态下翅片管式热沉传输几率计算分析

李春杨，杜春林，孙玉玮，柳晓宁，王晶，许忠旭，向树红

（北京卫星环境工程研究所，北京 100094）

分子流态下翅片管式热沉传输几率计算分析

李春杨，杜春林，孙玉玮，柳晓宁，王晶，许忠旭，向树红

（北京卫星环境工程研究所，北京 100094）

目的 研究空间环境模拟器翅片管式热沉传输特性，为进一步开展真空等效性分析等研究工作奠定基础。方法 根据热沉结构特点建立镜面反射气体输运通道模型，采用蒙特卡罗方法，对该模型的传输几率进行分析计算，并建立验证模型，对计算结果进行验证。结果 对于所选择的翅片管式热沉，其平面阵列的传输几率为0.030 116 4，柱面阵列的传输几率为0.017 988 6。结论 蒙特卡罗方法可以用于计算一定结构的翅片管式热沉的传输几率。通过传输几率的计算，可以将热沉等效为具有相应传输几率的可透射平面，从而在保证模拟精度的同时大大简化模拟计算强度，提高计算效率。

空间环境模拟器；热沉；分子流；传输几率

空间环境模拟器的主要功用之一是用来为航天器提供轨道条件下的真空和低温模拟环境，真空环境由真空获得系统维持，低温条件则由通有低温介质的热沉来提供[1—2]。通常，对地球轨道的真空环境模拟主要依托外装式低温泵实现，低温泵开口面积仅占总热沉面积的一小部分，模拟器内的绝大多数气体分子由发射表面到达低温泵的吸附表面的过程可能经历与热沉的碰撞、吸附、解吸附过程。为了对空间环境模拟器内部的真空度空间分布进行模拟分析，进而开展真空等效性分析等进一步的分析工作，首先应就热沉对于气体分子的传输特性对进行准确的研究分析。文中主要针对目前最常用的液氮管+翅片结构热沉进行研究，最终应用基于蒙特卡罗方法的MolFlow+软件计算了热沉的传输几率。

1　翅片管式热沉结构模型及传输特性

空间环境模拟器热沉形式有多种，包括平板形、斜板形、人字形、凹槽形、以及异形管加翅片形[3—6]，近年又出现了蜂窝流道热沉[7]。文中主要针对目前最常用的液氮管+翅片结构热沉进行研究，假设构成各区域热沉的结构单元尺寸参数一致，“平面热沉结构”和“柱面热沉结构”由热沉单元按线性阵列和圆周阵列构成。热沉单元及其构成的热沉结构如图1所示。

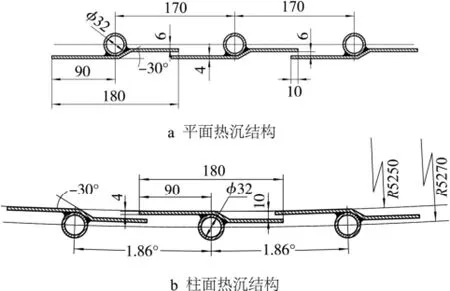
图1 空间环境模拟器翅片管式热沉结构模型Fig.1 The structure model of the finned tube heat sink

空间环境模拟试验所需真空压力通常低于6.5×10-3Pa，环境模拟设备的极限真空可达4.5×10-6Pa，在这样的压力条件下气体流态大多处于分子流状态。此时气体分子与固体壁面碰撞之后再发射时遵循“余弦定律”，并在发射前被固体壁面暂时吸附，使得气体分子与固体壁面之间可以进行充分的动量和能量交换[8]。

为了更好地研究分子流态下气体分子的传输特性，1932年，克劳辛（P. Clausing）提出了传输几率（又称流导几率、克劳辛因子，Clausing factor）的概念。传输几率的物理意义是：在分子流条件下，落入管道入口的气体分子能从管道出口逸出的概率[8—9]。假定有一真空元件，内壁既不吸附、也不脱附气体，或者内壁的吸附-脱附处于平衡状态，落入元件入口共 N个气体分子，其中由出口逸出N·Pr个分子，N·(1-Pr)个返回出口，则Pr称为此真空元件的传输几率。

翅片管式热沉单元结构之间的缝隙形成了空间环境模拟器内分子从试验空间向外部空间（热沉与容器壁间夹层等）的传输通道，同时也造成了热沉区域特殊的传输特性。通过计算热沉区域的通过几率，可以准确刻画热沉区域的分子传输特性，进而为空间环境模拟器内部的真空度空间分布分析计算及真空等效性分析等进一步的分析工作奠定基础。

传输几率的计算方法主要有解析法，即求解克劳辛积分方程和蒙特卡罗方法。考虑到热沉元件结构的复杂性，而且克劳辛积分方程在求解复杂管路传输几率时难以获得解析解甚至数值解，因此，文中将使用基于试验粒子蒙特卡罗算法（TPMC）的MolFlow+进行数值计算。

2　蒙特卡罗方法与其在真空技术中应用

蒙特卡罗（Monte Carlo）方法，是指一类以概率和统计理论为基础、依赖重复随机抽样过程而获得问题数值解的计算算法。其基本思想是：首先建立一个概率模型或随机过程，使它的参数等于问题的解；然后通过对模型或过程的观察，或抽样试验来计算所求参数的统计特征，最后给出所求解的近似值；而解的精度可用估计值的标准误差来表示[10]。在真空技术领域中，特别是分子流状态，微观粒子在真空空间以及在真空与固体交界面上的运动是随机现象（如真空中气体分子的空间碰撞）。因此，蒙特卡罗方法在求解真空技术领域内某些问题时，发挥着巨大的作用[11]。

1960年，Davis首先将蒙特卡罗方法应用到了真空科技领域，用于复杂管路流导的计算，从而有效规避了求解克劳辛方程所带来的复杂数学问题[12]。Bird[13]给出了用试验粒子蒙特卡罗（Test Particle MC，TPMC）方法研究通过静止圆管的自由分子流的方法。张波等[14]利用MC法对矩形、圆形和椭圆形截面管道的传输几率进行计算。目前，蒙特卡罗方法在真空技术领域迅速发展，其应用已遍及真空镀膜、真空泵结构设计与优化、真空系统设计，甚至拓展到真空学科与表面物理、气体放电、化学物理等交叉学科，而且正不断地触及新的研究领域。

3　MolFlow+软件及其计算正确性的验证

MolFlow+是一款可在超高真空条件下计算复杂形状容器内部稳态压力的 Windows程序，其算法的核心即蒙特卡罗方法。

MolFlow+是基于试验粒子蒙特卡罗（Test Particle Monte Carlo，TPMC）方法的超高真空（UHV）模拟程序。通过将真空元件描述为具有特定属性的、二维多边形构成的封闭空间，模拟分子流态下的气体分子在空间内的运动规律，并追踪虚拟试验粒子在气源与抽气口之间的运动轨迹，从而计算真空元件的传输几率（流导），并通过计算粒子与平面之间的碰撞（穿越）次数，表征真空元件内部的压力分布[15]。

MolFlow+软件的特点是可以在分子流条件下计算任意复杂三维几何形状容器内气体的稳态压力，其内核是蒙特卡罗方法（也可以选择角系数法）。对于MolFlow+计算正确性，MolFlow+的开发者已经公开发表了相关论文，并依据 MolFlow+所计算获得的直圆管道的传输几率（克劳辛系数）与其他研究获得的传输几率结果对比，间接验证了程序的正确性[16]。本研究也对MolFlow+软件计算管道传输几率的精确性进行了验证[8,17]，见表1。

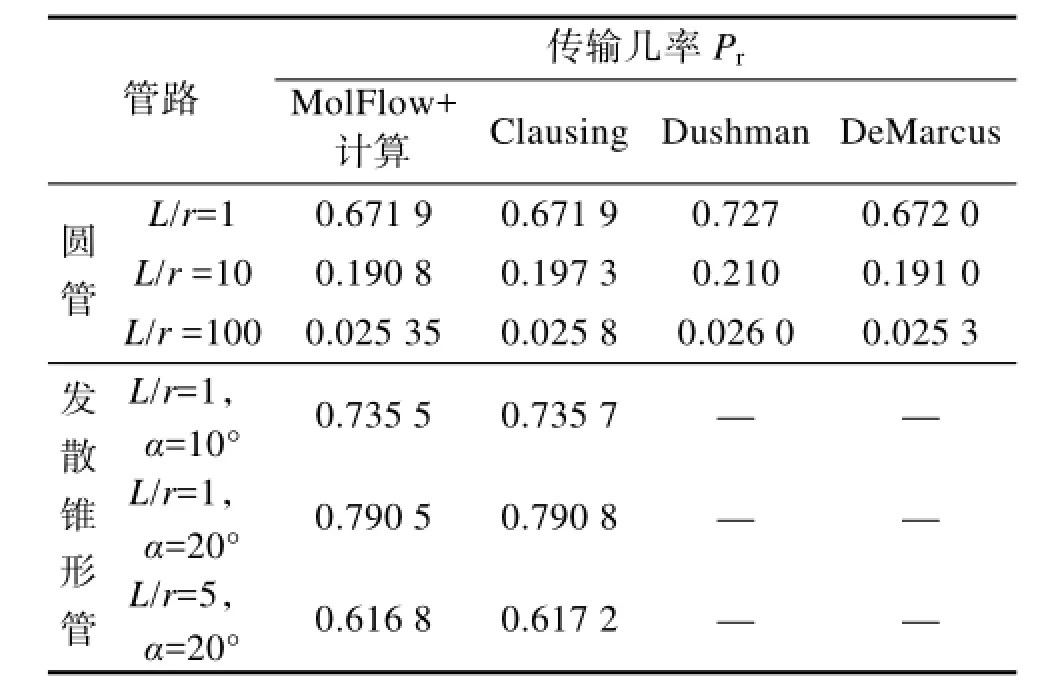
表1 利用MolFlow+计算管道传输几率与其他研究传输几率结果对比Table 1 The comparison of pipeline transmission probability with MolFlow+ and other research

从传输几率计算的角度，由以上验证结果可见，MolFlow+软件具有较高的计算精度，计算结果与相关研究结果基本一致，说明MolFlow+具有较高的可靠性和计算准确性。

4　分子流态下平面热沉传输几率计算

4.1 计算模型

沿着气体分子传输的方向（即垂直于热沉平面的方向），建立一段气体传输管路的计算模型，如图2所示。

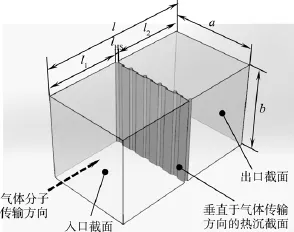
图2 平面热沉传输几率计算模型Fig.2 Transmission probability calculation model of plane heat sink

管路总长度为 l，由“热沉前管路”长度 l1、热沉厚度 lHS和“热沉后管路”长度 l2组成，即l=l1+lHS+l2（由图1可知，lHS=36 mm），管路横截面尺寸为a×b。为保证模型的的对称性，尽量消除模型尺寸对传输几率计算精度的影响。管路截面长度 a的取值为相邻热沉单元液氮管路轴线距离的整数倍，并使所建立的气体传输管路侧面与液氮管路轴线重合（如图2所示）。

通常情况下，模拟计算传输几率的条件是：入射分子的方向分布遵循余弦定律，且管路内壁均为漫反射边界，即气体分子与管路内壁碰撞之后再发射时也遵循余弦定律[16]。

如果按照上述条件设置计算模型的边界条件，则计算出的传输几率为整个管路的传输几率（即管路前段、热沉、管路后段，三段结构综合作用之后的传输几率），而并不是热沉结构的传输几率。这是因为部分落入管路入口的气体分子，与管路内壁发生碰撞时遵循漫反射规律，所以部分分子有可能在尚未碰撞到热沉之前，就已经折返回管路入口，如图3实线所示。同样，部分通过热沉结构的气体分子，由于与管路后段内壁发生碰撞之后，也可能重新返回到入口截面，如图3虚线所示。

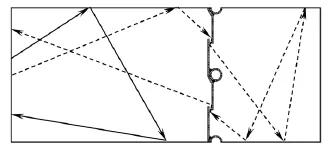
图3 计算模型内壁为漫反射边界时部分折返粒子轨迹Fig.3 Trajectories of the turn-back particles in the calculation model with diffuse boundary walls

综合以上分析，为保证落入管路入口的气体分子全部碰撞到热沉，同时保证通过热沉的分子全部逸出管路出口，则将管路的内壁设置为“镜面反射边界”条件，即管路的上、下、前、后内壁，对入射分子均为镜面反射。这样，虽然落入管路入口的气体分子遵循余弦定律，入射方向并不相同，但所有分子均“冲向”热沉，因此，在尚未接触到热沉之前，将不会有分子返回入口截面。同理，已经通过热沉的分子也不会返回管路入口截面。热沉传输几率计算边界条件见表2。

表2 分子流态下平面热沉传输几率计算边界条件设置Table 2 Boundary conditions of transmission probability calculation with plane heat sink under molecular flow

4.2 计算结果

为验证模型的正确性，通过改变模型的截面形状和尺寸，利用 MolFlow+软件，采用试验粒子蒙特卡罗（TPMC）方法进行多次模拟计算，所得结果见表3。计算结果显示，采用该模型情况下热沉的传输几率介于0.030 112 4～0.030 121 6之间。

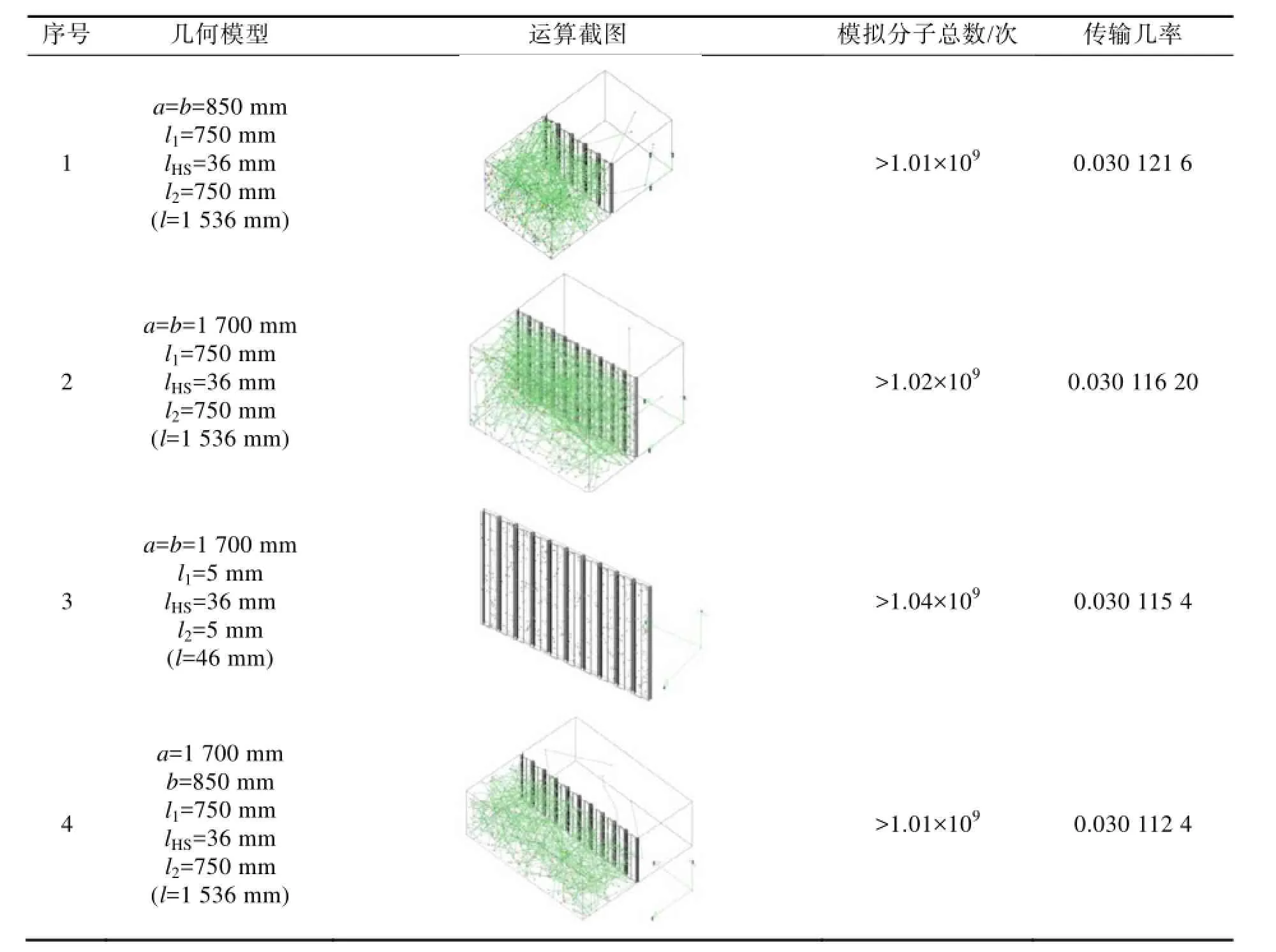
表3 分子流态下平面热沉传输几率计算结果Table 3 Results of transmission probability calculation with plane heat sink under molecular flow

4.3 计算结果验证

所建立的几何模型中，前、后段管路的长度都可能对热沉传输几率的计算结果产生某种程度影响。因此，如果最大限度地缩短前、后段管路的长度，并直接计算整个管路的传输几率，则计算值将越趋于热沉结构的传输几率。

按照表4设置边界条件，使用MolFlow+软件对不截面形状、尺寸的几何模型进行计算，所得热沉传输几率的计算结果见表5。

表4 验证计算边界条件设置Table 4 Boundary conditions of transmission probability calculation for verification

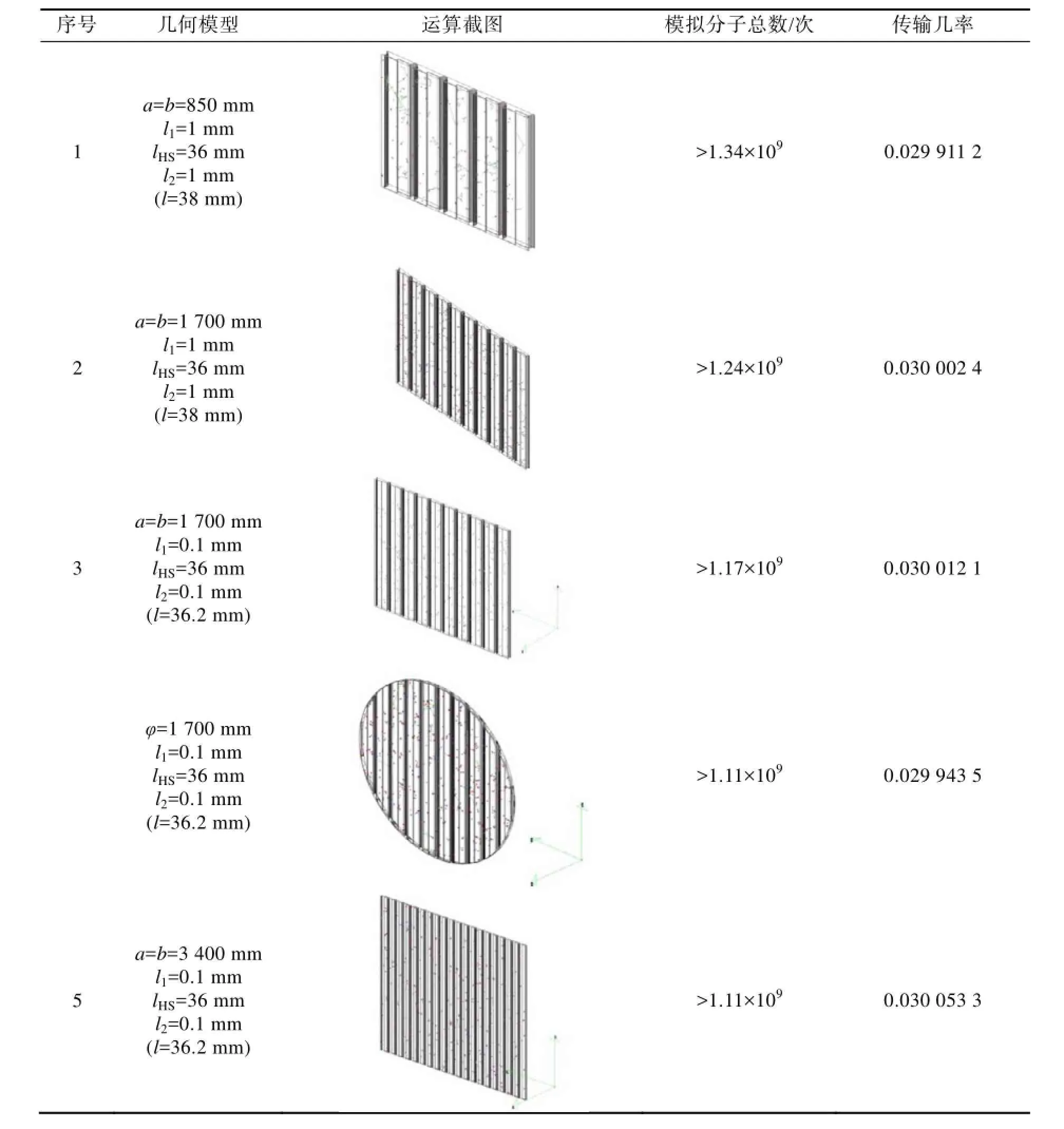
表5 验证结果Table 5 Results of the verification calculation

经验证，前后段管路压缩后所获得的热沉传输几率介于0.029 911 2～0.030 053 3之间。两种方法所计算的热沉传输几率的数值相差很小，说明了计算方法的合理性。

最初建立的计算模型管路侧面均设置为镜面反射，以保证模拟运算中所产生的所有气体分子均有机会“冲向”热沉，并且保证“穿过”热沉的分子均能够逸出管路出口；验证计算中尽管将管路模型的长度尽可能的缩小，但仍不能保证与管路侧面碰撞的气体分子在碰撞热沉之前不返回入口，但显然不能完全避免偏差的存在。因此，热沉传输几率取值为4.1节镜面反射模型计算结果的平均值：0.030 116 4。

5　KM6柱面热沉传输几率计算

采用与平面热沉计算相同的方法计算柱面热沉的传输几率，计算模型如图4所示。

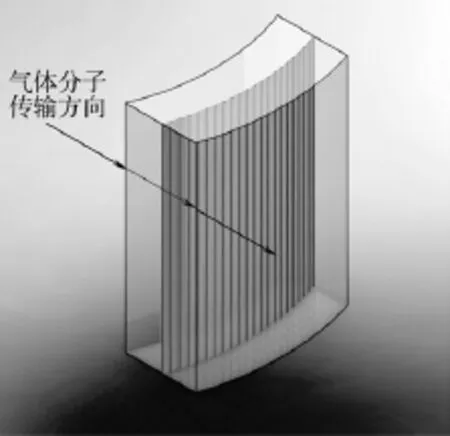
图4 柱面热沉传输几率计算模型Fig.4 Transmission probability calculation model of cylindrical surface heat sink

边界条件设置见表6。

表6 分子流态下柱面热沉传输几率计算边界条件设置Table 6 Transmission probability calculation boundary conditions of cylindrical heat sink under molecular flow

使用 MolFlow+软件计算热沉的传输几率，运算过程中截图如图5所示。计算过程中，模拟的粒子数>1.11×109次。通过计算，柱面热沉的传输几率为0.017 988 6。

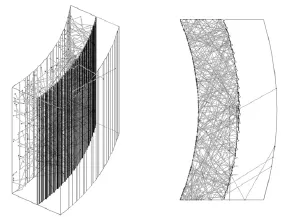
图5 柱面热沉传输几率计算截图Fig.5 Screenshot of the cylindrical heat sink transmission probability calculation

6　结语

蒙特卡罗方法可以用于计算一定结构的翅片管式热沉的传输几率。通过传输几率的计算，可以将热沉等效为具有相应传输几率的可透射平面，从而在保证模拟精度的同时大大简化模拟计算强度，提高计算效率。该方法也可以为其他类似真空结构的分析计算提供参考。

[1] 黄本诚, 马有礼. 航天器空间环境试验技术[M]. 北京:国防工业出版社, 2002. HUANG Ben-cheng, MA You-li. Space Environment Test Technology of Sapcecraft[M]. Beijing: National Defense Industry Press, 2002.

[2] 黄本诚. 载人航天器空间环境试验设备的研制[J]. 航天器环境工程, 2002, 19(2): 11—18. HUANG Ben-cheng. The Development of Space Environment Test Facility for Manned Spacecraft[J]. Spacecraft Environment Engineering, 2002, 19(2): 11—18.

[3] 黄本诚. KM6载人航天器空间环境试验设备[J]. 中国空间科学技术, 2002, 22(3): 1—5. HUANG Ben-cheng. Space Environment Test Facility for Manned Spacecraft[J]. Chinese Space Science and Technology, 2002, 22(3): 1—5.

[4] 黄本诚, 童靖宇. 空间环境工程学[M]. 北京: 中国科学技术出版社, 2010. HUANG Ben-cheng, TONG Jin-yu. Space Environment Engineering[M]. Beijing: China Science and Technology Press, 2010.

[5] 黄本诚. 神舟飞船特大型空间环境模拟器[J]. 航空制造技术, 2005(11): 34—37. HUANG Ben-cheng. Ultra-large Scale Space Environment for Shenzhou Spaceship[J]. Aeronautical Manufacturing Technology, 2005(11): 34—37.

[6] 邹定忠, 刘敏, 刘国青. 热沉设计技术[J]. 中国空间科学技术, 2002, 22(3): 20—26. ZOU Ding-zhong, LIU Min, LIU Guo-qing. Design of a Thermal Shroud Attached to KM6 Space Simulator[J]. Chinese Space Science and Technology, 2002, 22(3): 20—26.

[7] 张磊, 刘然, 刘敏. 蜂窝流道热沉强化传热数值模拟[J].装备环境工程, 2013, 10(4): 121—125. ZHANG Lei, LIU Ran, LIU Min. Numerical Simulation of Heat Transfer Enhancement in Honeycomb Shroud [J]. Equipment Environment Engineering, 2013, 10(4): 121—125.

[8] 徐钟济. 蒙特卡罗方法[M]. 上海: 上海科学技术出版社, 1985: 5—7. XU Zhong-ji. Monte Carlo Method[M]. Shanghai: Shanghai Scientific & Technical Publishers, 1985: 5—7.

[9] 王继常. 蒙特卡罗方法及其在真空技术中的应用[M].沈阳: 东北大学真空技术与设备教研室, 1997. WANG Ji-chang. Monte Carlo Method and Its Application in Vacuum Technology[M]. Shenyang: Teaching and Research Group of Vacuum Technology and Equipment, Northeast University, 1997.

[10] NIEWINSKI M, SZWEMIN P. Moly Flower—The Computer Program for Calculation of Vacuum System Conductance[J]. Vacuum, 2002, 67(3): 327—332.

[11] BIRD G A. Molecular Gas Dynamics[M]. London: Clarendon Press (Oxford University Press), 1976.

[12] 张波, 王洁, 尉伟, 等. 蒙特卡罗法计算分子流状态下真空管道的传输几率[J]. 真空科学与技术学报, 2014, 34(66): 571—574. ZHANG Bo, WANG Hao, YU Wei, et al. Monte Carlo Simulation of Transmission Probability of Molecular Gas Flow Through Vacuum Pipes[J]. Chinese Joural of Vacuum Science and Technology, 2014, 34(66): 571—574.

[13] ADY M, KERSEVAN R. Introduction to the Latest Version of the Test-Particle Monte Carlo Code Molflow+[R]. Geneva, Switzerland: CERN, 2014.

[14] KERSEVAN R, PONS J L. Introduction to Molflow+: New Graphical Processing Unit-Based Monte Carlo Code for Simulating Molecular Flows and for Calculating Angular Coefficients in the Compute Unified Device Architecture Environment[J]. Journal of Vacuum Science & Technology A, 2009, 27(4): 1017—1023.

[15] 达道安. 真空设计手册[M]. 第3版. 北京: 国防工业出版社, 2006. DA Dao-an. Vacuum Design Maneul[M]. The 3rdEdition. Beijing: National Defense Industry Press, 2006.

[16] 王晓冬, 巴德纯, 张世伟, 等. 真空技术[M]. 北京: 冶金工业出版社, 2006. WANG Xiao-dong, BA De-chun, ZHANG Shi-wei, et al. Vacuum Technology[M]. Beijng: Metallurgical Indrustry Press, 2006.

[17] 王继常. 真空系统设计[M]. 沈阳: 东北大学出版社, 2002. WANG Ji-chang. Vacuum System Design[M]. Shenyang: Northeast University Press, 2002.

Calculation of Transmission Probability of the Finned Tube Heat Sink in Molecular Flow

LI Chun-yang, DU Chun-lin, SUN Yu-wei, LIU Xiao-ning, WANG Jing, XU Zhong-xu, XIANG Shu-hong
(Beijing Institute of Satellite Environment Engineering, Beijigng 100094, China)

Objective To study the transmission probability of the finned tube heat sink and set up the foundation of the future research such as the analysis of the vacuum equivalence of the space environment simulator. Methods Based on the structure of the heat sink, model of the transmission passage with total reflection passage walls was set up. Then the transmission probability was calculated by Monte Carlo method. A verification model was established to verify the calculation results. Results The transmission probability of the plane heat sink panel with the specific structure was 0.030 116 4, while that of the cylindrical one was 0.017 988 6. Conclusion Monte Carlo method can be used to calculate the finned tube heat sink. Through the calculation, the heat sink can be equalized as a penetrable surface which will greatly simplify the calculation of the whole vacuum simulator in further numeric analysis.

space environment simulator; heat sink; molecular flow; transmission probability

2016-08-22；Revised：2016-08-30

10.7643/ issn.1672-9242.2016.05.013

TJ04；TG172.4

A

1672-9242(2016)05-0081-07

2016-08-22；

2016-08-30

国防科工局技术基础“十二五”科研项目（JSJC2013203B002）

Fund：State Administration of Science， Technology and Industry for National Defense（JSJC2013203B002）

李春杨（1972—），男，硕士，高级工程师，主要研究方向为空间环境模拟与试验技术。

Biography：LI Chun-yang （1972—）， Male， Master， Senior engineer， Research focus: space environment simulation and test.