基于最大谱的非平稳随机振动数据分析处理方法研究
2016-11-12徐俊傅耘张建军孙建勇王星皓
徐俊,傅耘,张建军,孙建勇,王星皓
(中国航空综合技术研究所,北京 100028)
基于最大谱的非平稳随机振动数据分析处理方法研究
徐俊,傅耘,张建军,孙建勇,王星皓
(中国航空综合技术研究所,北京 100028)
目的 解决非平稳随机振动环境实测数据无法采用功率谱密度分析方法的问题。方法 基于最小均方误差准则,归纳总结FFT和数字滤波两种最大谱分析方法。通过对比两种方法在不同分辨率带宽时计算的优缺点,并分析其误差。对优选出来的最大谱分析方法进行举例验证。结果 理论分析和仿真结果均表明基于比例分辨率带宽的FFT最大谱分析方法的误差最小。将FFT最大谱分析方法应用于某型炸弹9个架次自由飞振动数据的处理和环境条件确定中,结果合理有效。结论 可用比例分辨率带宽的FFT法分析非平稳随机振动环境实测数据,为基于最大谱制定型号振动环境试验条件提供指导。
非平稳随机信号;最大谱; FFT;数字滤波
近年来,随着装备作战需求的提高,各个航空航天型号所面临的环境愈加复杂多样,其环境适应性要求也越来越高,而GJB 150A/899A是基于美国装备的特点制订的标准,不完全适用于国内装备产品,因而基于实测数据确定环境条件也显得愈加重要。对于运载器、火箭、炸弹等装备在飞行过程中,经历热、振和噪声等综合环境尤其复杂,并且采集到的振动样本少、飞行时间短、状态变化大,主要表现为非平稳随机振动数据。因此,有必要选择合理的数据分析方法对非平稳随机振动数据进行处理,为振动环境条件确定提供基础[1—3]。
目前,功率谱密度分析方法是处理平稳随机振动数据的重要工具,但不适用于非平稳随机振动环境实测数据的处理。对于非平稳随机信号,大多通过时频分析识别不同时刻的不同频率成分。装备环境适应性的验证,主要是利用特定量值的等效平稳振动代替难以复现的非平稳随机振动进行环境验证试验。因此需要对现有的时频分析算法进行改进,根据相关设计规范和试验标准的应用指南,推荐采用基于短时傅里叶变换(STFT)的最大谱作为非平稳随机振动数据的主要分析处理方法。国内外关于最大谱的工程应用研究较少,难以指导设计和试验人员合理分析非平稳随机信号,并得出正确的环境条件。
文中首先结合GJB/Z 222—2005《动力学环境数据采集和分析指南》附录B[4]中的非平稳随机振动相关资料,归纳出两种最大谱分析方法。其次详细介绍了这两种方法的分析流程,给出了最大谱分析方法的工程应用建议。最后针对某型号炸弹实测的非平稳随机振动数据,选择合理的分析方法计算最大谱,并确定其环境条件。
1 最大谱分析方法
1.1 分析流程
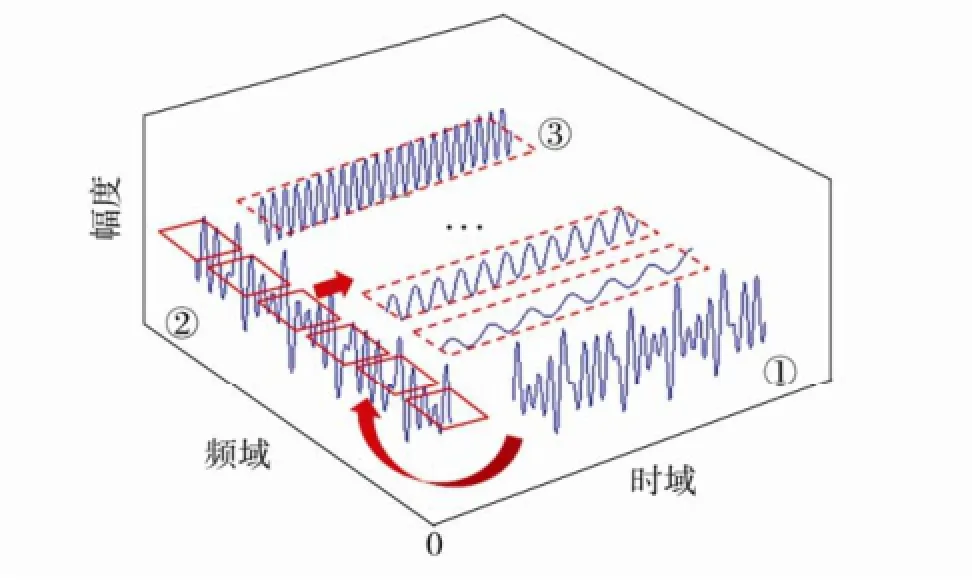
非平稳振动的最大谱通常可解释为设计和试验所需要的等效平稳载荷自谱,为非平稳事件中每个频率分辨率带宽下最大的谱值,因此采用最大谱的均方根值应该大于原始信号的均方根值。主要分析流程如图1所示,首先剔除非平稳随机信号中的瞬态事件;然后确定在最大谱分析过程中的参数,即平均时间T和分析带宽B;最后根据选用的最大谱计算方法计算自谱,并且通过平均处理提高统计精度得到最大谱结果。
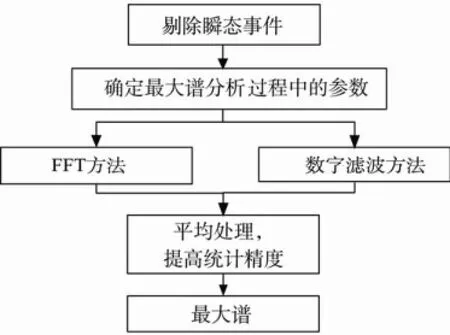
图1 非平稳随机信号最大谱分析流程Fig.1 The analysis process of maximum spectral fornonstationary random data
对于随机信号x(t)的功率谱密度G(f)是x(t)通过中心频率为f、分析带宽为B的窄带滤波器,当B趋于0和平均时间趋于无限时的均方值[5],数学上可表示为:

式中:T为平均时间;B为分析带宽;x2(f,t,B)为经窄带滤波器后信号的瞬时平方值。
在Bendat和Piersol[6]的论文中已经表明,公式(1)在T→∞并且B→0,BT→∞的极限条件下得到了随机振动的真实功率谱密度。在现实中这些极限条件无法实现,即对于一个实际的PSD估计,BT必须是有限的,并且带宽B为非0,因此实际的PSD估计存在随机(统计抽样)误差、时间分辨偏置误差和频率分辨偏置(频域平滑)误差[7—9]。为了将功率谱密度估计的总误差最小化,需要确定最大谱分析的最佳参数(平均时间 T和分析带宽B)。
1.2 参数确定
在计算最大谱的过程中,选取合理的参数能够减小功率谱密度估计的总误差,主要包括平均时间和频率分辨率带宽的确定。
1.2.1 平均时间的确定
在整个非平稳事件上,在所要求的频率分析范围内每一个分析带宽上,通过滑动平均计算时变自谱[10]。对所测的非平稳随机振动信号,推荐用下列方法选择谱分析用的固定平均时间[11]:在用解析法或试凑法计算振动信号总均方根值时,对分段线性平均,近似取最佳平均时间T0;当计算整个频带的谱时,平均时间取2T0。
1.2.2 频率分辨率带宽的确定
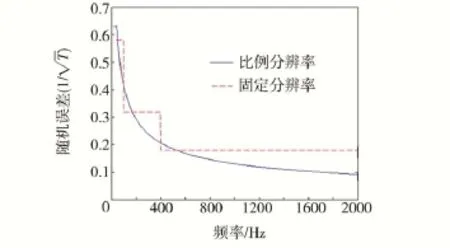
1) 比例分辨率带宽。为了使典型运载器发射时振动数据谱分析的均方误差接近最小,相应的比例带宽是1/12倍频程带宽(B0=0.058f),而当小于43 Hz时,修正为常带宽(B0=2.5 Hz)[12]。
2) 固定分辨率带宽。这种方法实质为常分辨率带宽,在频率范围从20~2000 Hz的谱分析,要达到可接受的均方误差,可用表1中三种常带宽来实现[13]。

中心频率/Hz 分析带宽/Hz 20≤f<100 3 100≤f<400 10 400≤f≤2000 30
表1 固定分辨率带宽
Table 1 Fixed resolution bandwidth

式中:i=0,1,2,…,(n-1);n为总段数;M为段长(每段之间的数据值数目)。
以上两种分辨率带宽能够在一定程度上减小由于分析带宽无法趋近于 0而带来的频率分辨偏置误差。对于统计随机误差,则采样分段线性平均的方法,对离散时间序列测量数据x(nΔt),n=1,2,…,滑动平均的等效值可在N个数据点上(T=N·Δt)用分段的无加权(线性的)平均来计算[14—15]:
1.3 最大谱计算方法
基于最小均方误差准则,通过功率谱密度的两种表示形式,归纳出两种最大谱分析方法,分别是FFT法和数字滤波法。
1.3.1 FFT最大谱分析法
非平稳随机振动信号的时变自谱可以用 FFT法来估计:
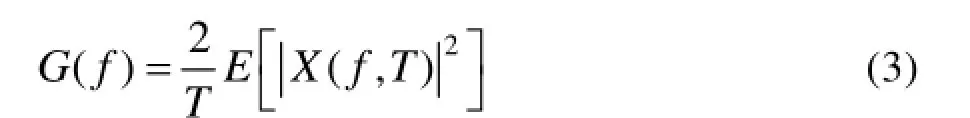
式中:E[|X(f,T)|2]为傅里叶变换后平方值的期望。式(5)的计算框图如图2所示。
1.3.1.1 集合平均FFT法

图2 时变自谱密度函数估计程序(FFT法)Fig.2 Procedure for estimating time-varying autospectral density function (FFT)
计算振动数据的自谱最常用的方法是FFT法。其主要思路是将时域信号分段,然后分别求各个子样本的自谱,最后进行平均处理提高精度,如图 3所示。计算步骤为:把感兴趣的时间段分隔成 nd个不相连的数据段,每段长为T;计算每段的原始自谱;对原始谱进行集合平均,得到时间为T0=ndT的平均自谱。当采用滑动平均时,步长为 0.2ndTs或小于0.2ndN。

图3 集合平均FFT法Fig.3 The drawing of conventional FFT computation
1.3.1.2 单次FFT法
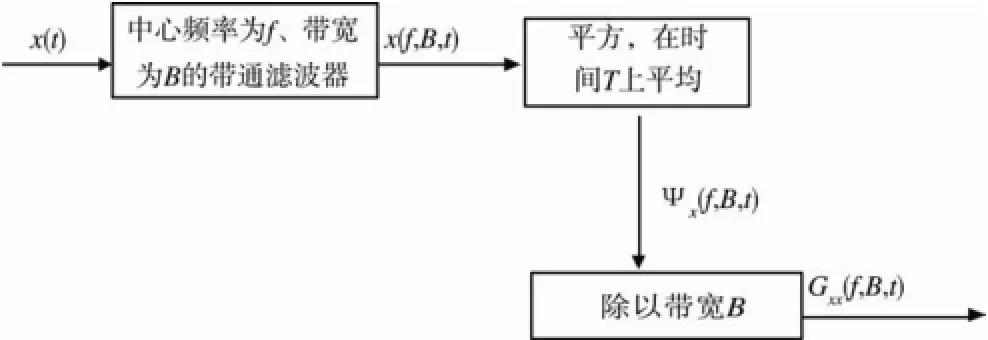
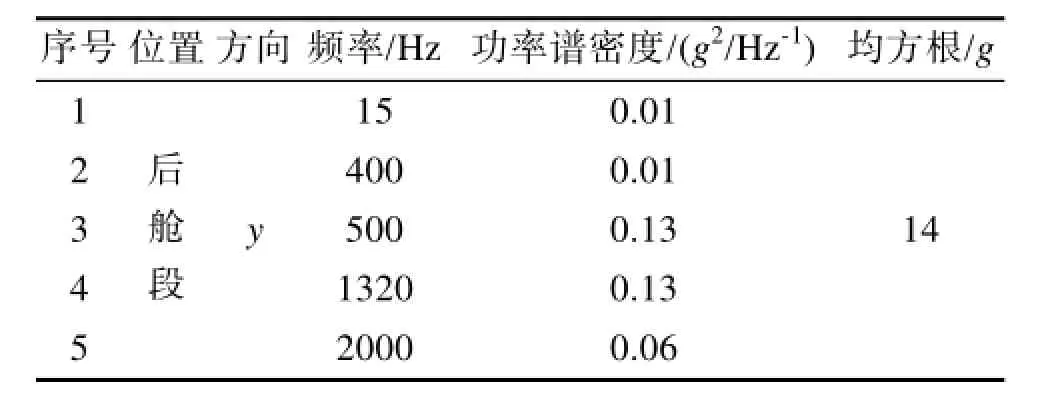
单次FFT法进行谱分析如图4所示,其主要思路是将整体样本进行单次FFT,然后在频域上滑动平均求自谱。计算步骤为:将原始信号进行单次FFT变换;在平均时间为T上,采用比例分辨率带宽计算原始自谱,得到一系列频率间隔为 Δf=1/T的离散谱分量(该计算应用矩形窗来完成,不应加为抑制旁瓣泄漏的加窗处理);按要求把相邻的谱分量一起平均,以得到频率分辨率带宽下谱分量的集合平均,它近似于 1/12倍频程;最后从两个或更多个的搭接段来计算频率平均自谱,每段长为N·Δt=T 1.3.2 数字滤波最大谱分析法 非平稳随机振动信号的时变自谱可以用滤波法来估计: 式中:x2(t,B,f)表示经过中心频率为f、带宽为B的窄带滤波器后的信号瞬时平方值。 图4 单次FFT法Fig.4 The drawing of single FFT computation 式(4)的计算框图如图5所示。 图5 时变自谱密度函数估计程序(数字滤波法)Fig.5 Procedure for estimating time-varying autospectral density function (digital filter) 1.3.2.1 时域滤波法 使用数字滤波法进行最大谱分析,当采用时域滤波时,原始信号通过窄带滤波器后,求其瞬时平方值,在时间T上平均,如图6所示。计算步骤为:x(t) 通过中心频率为f、带宽为B的时域带通滤波器,得到x(f, B, t);对时域滤波后(采用1/12倍频程滤波器)的信号进行平方,在时间T上平均,得到自谱φx(f, B, t);将自谱除以带宽B得到Gxx(f,t)。 1.3.2.2 频域滤波法 图6 时域滤波法Fig.6 The drawing of time-domain filter 使用频域数字滤波法时,与时域滤波不同的是,首先将原始信号进行快速傅里叶变换,然后采取频域滤波,得到各个中心频率上的时域信号,如图7所示。计算步骤为:将原始信号进行单次FFT变换,在频域上进行滤波,采用固定分辨率带宽;然后利用傅立叶逆变换得到时域信号,在平均时长T0上平均;除以带宽。 图7 频域滤波法Fig.7 The drawing of frequency-domain filter 与 FFT最大谱分析法相比,数字滤波方法由于滤波器的频率响应函数不可能是理想的矩形,在分析的过程中会额外引入静态误差,而 FFT法则不存在滤波误差。因此在平均时间和分析带宽等参数相同的条件下,选用 FFT最大谱分析法的误差会相对较小。另外,集合平均 FFT法对总样本的时间进行分段,计算每个频率分辨率带宽下最大的谱值。单次 FFT法则在计算过程中丢失了很多时域上的信息,只是对分析带宽内的多个谱值进行平均,因此单次 FFT法计算的最大谱值偏小,而集合平均FFT法的最大谱值更为准确。 1.4 最大谱分析误差 在非平稳随机振动数据谱分析中,分辨率带宽是可选的。在分析中,存在时间分辨率偏置误差和随机误差,这些误差可用下列归一化形式来估算。 时间分辨率偏置误差: 随机误差: 式中:b[Ĝxx(f,t)]为 Ĝxx(f,t)估计的偏置误差,b[Ĝxx(f,t)]=E[Ĝxx(f,t)]-Gxx(f,t);σ[Ĝxx(f,t)]为 Ĝxx(f,t)估计的标准差; B为谱估计的频率分辨率带宽;T为谱估计的时间分辨率(平均时间)。 为了评估最大谱分析过程中的时间分辨偏置误差,选择式(7)中的 d2[Gxx(f,t)]/dt2的值是非常必要的,而二次求导的值与实际样本分析的自谱值密切相关。在分析样本相同、平均时间相同的情况下,各方法计算的时间分辨偏置误差在理论上基本相同。 分析式(6)可知,最大谱分析过程中的随机误差与平均时间和分析带宽相关,通常各分析方法选取的平均时间是相同的,因此无论是 FFT还是数字滤波最大谱分析方法,随机误差主要与分析带宽有关。对比上述几种最大谱分析方法的随机误差,其关系见表2。以中心频率为横坐标,随机误差为纵坐标,绘制比例分辨率带宽和固定分辨率带宽下的随机误差如图所示。 表2 FFT和数字滤波最大谱分析方法的随机误差对比Table 2 The comparison of random error for FFT and digital filter maximum spectral 图8 不同分析带宽下的随机误差Fig.8 The random error of different bandwidths 通过对比分析,当各分析方法的平均时间相同时,在大部分频率范围内,比例分辨率带宽最大谱分析的随机误差较小。 综上所述,从理论分析的角度判断可知,选用比例分辨率带宽的 FFT最大谱分析方法时,分析过程中产生的随机误差较小,且其误差随中心频率的增大而不断减小。 根据某型号炸弹在自由飞过程中采集的振动数据,结合其物理飞行过程,包括点火、舵机启控等瞬态事件,设计如下非平稳随机仿真数据,其振动曲线如图所示。由于其中包括瞬态事件,因此截取30~49 s之间的数据进行最大谱分析。 图9 某型炸弹实测非平稳随机信号Fig.9 Non-stationary random data of a certain missile 经过计算,采用上述的最大谱分析方法进行处理,得到各最大谱分析方法计算结果见图和表3。 图10 各方法计算得到的最大谱图Fig.10 The maximum spectrals 表3 各最大谱分析方法计算结果Table 3 The results of maximum spectrals computation 在非平稳事件期间,每个频率上谱密度值达到最大值时,它的偏置误差一般将是最大的,因此在最大谱的每个频率上计算得到的误差代表着最大误差。各种方法的时间偏置误差和随机误差如图和图12所示。 图11 时间偏置误差Fig.11 Time resolution bias error 图12 随机误差Fig.12 Random error 对比分析结果可知: 1) 集合平均FFT法、单次FFT法和数字滤波法(比例分辨率带宽)进行最大谱分析得到的均方根值较为接近,且随机误差均随着中心频率的增大而减小。在100~2000 Hz范围内时间偏置误差小于5%;在中心频率较小时,时间偏置误差和随机误差均较大。 2) 在所有的方法中,单次FFT法的计算结果与原始信号的均方根值最接近,因为单次 FFT法进行了频率平均,并不是每个频率带宽下的最大的谱值,因此均方根值与原始信号最接近。 3) 数字滤波法中的频域滤波计算的结果偏差最大,这是由于原始信号进行滤波时引入了静态误差。 4) 无论是FFT法还是数字滤波法,选用固定分辨率带宽计算出的最大谱均方根偏大,因为在平均时间相同时,固定分辨率带宽引入了更大的随机误差。 5) 通过对比时间偏置误差和随机误差的大小,随机误差普遍较大,是仿真实例最大谱计算总误差的主要组成部分。 综上所述,通过仿真分析,各种最大谱分析方法的误差与理论分析一致,推荐在工程应用中选用FFT比例分辨率带宽的最大谱分析方法。 针对某型炸弹自由飞过程,共实测9个架次的数据,选用基于 FFT比例分辨率带宽的最大谱分析方法进行计算,并确定其环境试验条件。选取该型炸弹所有实测架次的后舱段y向实测数据,分别计算其最大谱并取包络,得到最终的试验规范谱如图所示。 图13 后舱段y向规范谱Fig.13 Normalized spectral of rear section in y 考虑到外场实测与实验室模拟试验的差别,以及实测型号的样本数量有限,分别在实测规范谱谱型上乘以载荷分散系数1.2,安全系数1.2,得到后舱段y向试验条件见表4。 表4 后舱段y向试验条件Table 4 The value of normalized spectral of rear section in y 通过对比 FFT和数字滤波两种最大谱分析方法的优缺点并分析其误差,可得以下结论。 1) 与数字滤波最大谱分析方法相比,选用 FFT(比例分辨率带宽)最大谱分析方法的误差最小。 2) 对比两种方法在不同分辨率带宽时计算的误差,理论分析和仿真结果一致,验证了最大谱分析方法的有效性。 3) 将 FFT最大谱分析方法应用于某型炸弹 9个架次自由飞振动数据的处理和环境条件确定中,获得的自由飞振动试验条件合理有效。 [1] 郭迅, 郭强岭. 空空导弹振动试验条件分析[J]. 装备环境工程, 2012, 9(3): 99—103. GUO Xun, GUO Qiang-ling. Analysis of Vibration Test Condition of Air-to-Air Missile[J]. Equipment Environmental Engineering, 2012, 9(3): 99—103. [2] 郭强岭, 李立民. 空空导弹挂飞振动试验条件探讨[J].航空兵器, 2003(6): 21—23. GUO Qiang-ling, LI Li-min. Discussion of Vibration Test Condition for Air-to-Air Missile[J]. Aero Weaponry, 2003(6): 21—23. [3] 郭强岭. 空空导弹振动试验条件确定方法[J]. 航空标准化与质量, 2006(3): 34—37. GUO Qiang-ling. Determination of Vibration Test Condition for Air-to-Air Missile[J]. Aeronautic Standardization & Quality, 2006(3): 34—37. [4] GJB/Z 222—2005, 动力学环境数据采集和分析指南[S]. GJB/Z 222—2005, Guidelines for Dynamic Environmental Data Acquisition and Analysis[S]. [5] 施荣明. 飞机结构振动设计与试验[M]. 北京: 航空工业出版社, 2014: 110—111. SHI Rong-ming. Aircraft Structure Design and Vibration Test[M]. Beijing: Aviation Industry Press, 2014: 110—111. [6] BENDAT J S, PIERSOL A G. Random Data: Analysis and Measurement Procedures[M]. 2nd Ed. New York: Wiley, 1986. [7] BENDAT J S, PIERSOL A G. Engineering Applications of Correlation and Spectral Analysis[M]. 2nd Ed. New York: Wiley, 1993. [8] FORLIFER W R. The Effects of Filter Bandwidth in the Spectrum Analysis of Random Vibration[R]. Washington D C: Department of Defense,1964. [9] SCHMIDT R. Resolution Bias Errors in Spectral Density, Frequency Response and Coherence Function Measurements, III: Application to Second-order Systems[J]. Journal of Sound and Vibration, 1985, 101: 377—404. [10] 苏成, 徐瑞. 非平稳激励下结构随机振动时域分析法[J].工程力学, 2010, 27(12): 77—83. SU Cheng, XU Rui. Random Vibration Analysis of Structures Subjected to Non-stationary Excitations by Time Domain Method[J]. Engineering Mechanics, 2010, 27(12): 77—83. [11] 张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998. ZHANG Xian-da, BAO Zheng. Analysis Procedures for Non-stationary Signal[M]. Beijing: National Defence Industry Press, 1998. [12] 张海勇, 李勘. 非平稳随机信号的参数模型分析方法[J].系统工程与电子技术, 2003, 25(3): 386—390. ZHANG Hai-yong, LI Kan. Analytical Methods for the Non-Stationary Random Signals Based on Parametric Models[J]. Systems Engineering and Electronics, 2003, 25(3): 386—390. [13] ALLAN G P. Optimum Data Analysis Procedures for Titan IV and Space Shuttle Payload[M]. California: Jet Propulsion Laboratory, California Institute of Technology, 1991. [14] HARRY H, ALLAN G P, JAMES H W, et al. Handbook of Dynamic Data Acquisition and Analysis[M]. USA: Institute of Environmental Sciences, 1994. [15] 张海勇. 基于局域波法的非平稳随机信号分析中的若干问题的研究[D]. 大连: 大连理工大学, 2001. ZHANG Hai-yong. Research on the Problems of NonStationary Random Signal Analysis and Processing Based on Local Wave Method[D]. Dalian: Dalian University of Technology, 2001. The Research of Processing Method Based on Maximum Spectral for Non-stationary Random Vibration Data XU Jun, FU Yun, ZHANG Jian-jun, SUN Jian-yong, WANG Xing-hao Objective To solve the problem that the environmental measurement of non-stationary random vibration data can’t deal with power spectral density. Methods Two methods of maximum spectral analysis were summed up, namely FFT and digital filter which were based on minimum mean-square error criterion. The advantages, disadvantages and error of two methods with different bandwidth were discussed, and then examples were given to testify the better method. Results The theoretic analysis and simulation results showed that: the error was minimum with conventional FFT computations (proportional resolution bandwidth). The conventional FFT computations were applied to 9 sorties of non-stationary vibration data processing and environmental condition determination for a certain missile, and the result was reasonable and effective. Conclusion The conventional FFT is the best method to deal with non-stationary random vibration data, which provides guidance for formulating environmental condition based on maximum spectral. non-stationary random vibration data; maximum spectral; FFT; digital filter 2016-08-16; Revised:2016-08-16 10.7643/ issn.1672-9242.2016.05.009 TJ86 A 1672-9242(2016)05-0054-07 2016-08-16; 2016-08-16 徐俊(1990—),男,湖北武汉人,硕士研究生,主要研究方向为装备环境工程。 Biography:XU Jun(1990—), Male, from Wuhan, Hubei, Maser graduate student, Research focus: equipment environmental engineering.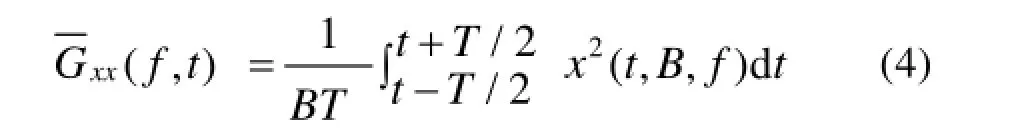



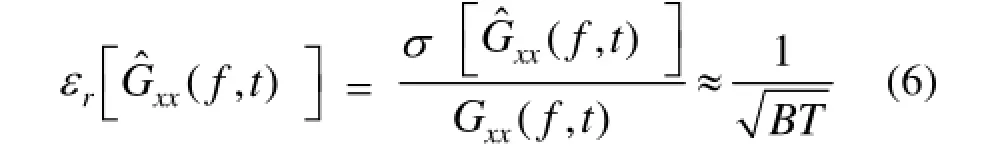

2 仿真实例





3 应用举例

4 结论
(China Aero-Polytechnology Establishment, Beijing 100028, China)
