地图着色问题的DNA计算
2016-11-11马莹,方欢
马 莹,方 欢
安徽理工大学理学院,安徽淮南,232001
地图着色问题的DNA计算
马莹,方欢
安徽理工大学理学院,安徽淮南,232001
提出了将地图着色问题转化为顶点着色问题,然后把顶点着色问题转化为求最大独立集问题。最大独立集问题的解法采用改进的粘贴DNA计算,即全信息化的DNA粘贴计算。DNA粘贴计算设计了主链和存储链,而且在生物计算中采用并行处理。最后给出了一个实例,详细说明了地图着色问题的解法,得出了最终的解。
DNA计算;粘贴计算;地图着色问题;顶点着色;最大独立集
1994年,Adleman首次用DNA计算解决有向图的哈密顿问题[1],此后许多研究者对DNA计算进行研究。粘贴模型是由Roweis等人于1996年提出的一种DNA计算模型[2],给出了图的最大团与最大独立集粘贴DNA计算模型[3],特别是许进教授的文献[4-5]对DNA粘贴计算的研究有很大的意义。文献[6]把地图着色问题转化成可满足性问题,并采用多级分离装置来实现,文献[7]采用分子信标表面技术实现地图着色问题的DNA计算,文献[8]给出了图的最小顶点覆盖问题的DNA计算,文献[9] 给出了最大匹配问题的粘贴DNA算法。文献[10] 用微流控DNA计算解决图着色问题的DNA算法。本文提出了全信息化的DNA粘贴计算模型。
1 基于DNA计算的粘贴模型
1.1粘贴模型
粘贴模型的DNA分子的编码是一种单链和双链混合的序列,存储混合物由两种类型的单链组成:一种是存储链,另一种是粘贴链。一个存储链含有K个不重叠区域的单链DNA分子,其中不重叠区域有M个碱基;粘贴链也是单链DNA分子,可以设计M个碱基的粘贴链与存储链中的DNA单链分子恰好构成互补。存储混合物由粘贴链和存储链混合构成,如果每个粘贴链的M个碱基恰与上述存储区中的一个互补,设其对应位为“1”;如果没有粘贴链与匹配位互补,则设其存储复合物表示二进制数的对应位为“0”。假设存储复合物的DNA分子编码如下:
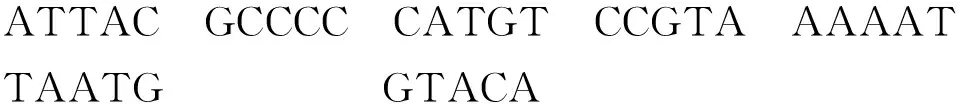
这个存储混合共有5位,每位含5个碱基。DNA单链ATTAC GCCCC CATGT CCGTA AAAAT是存储链,较短的DNA单链TAATG和单链GTACA是粘贴链,则这个存储物由单链和双链混合而成。如果用二进制数来表示位点,则双链表示数字“1”,单链表示数字“0”,这个存储复合物可以用二进制数表示为10100。
1.2生物操作
对于DNA计算,首先要对研究对象编码,其次进行一系列生物操作生成解,最后检测解。在粘贴计算中,一般把初始试管记为输入试管,常用四种基本生物操作。
合并把两个试管的溶液倒入一个试管中。两个输入试管T1和T2中的存储复合物被合并成一个新的输出试管T0。
分离一般通过设计探针来实现。对于输入试管T0和整数i,1≤i≤K,如果执行分离生物操作的话,将会产生两个新的试管+(T0,i)和-(T0,i)。其中.tif,+(T0,i)表示试管T0中第i位为“1”的所有存储复合物试管,即第i位为双链的存储复合物;-(T0,i)含有试管T0中第i位为“0”的所有存储复合物,即第i位为单链的存储复合物。分离操作破坏了原始的输入试管。
设置通过杂交将原来位点为单链的所有存储复合物设置成双链。对于原来试管T0和整数i,1≤i≤K,设置操作产生一个新试管,即无论原来第i位为“1”还是“0”,它将原来试管中所有存储复合物的第i位都置为“1”,得到的新试管第i位都为“1”。
清除通过加热将将存储复合物中位点“1”的双链变为单链。对于试管T0和整数i,1≤i≤K,清除操作产生新试管clear(T0,i),试管T0中所有存储复合物的第i位上的粘贴链都被去掉。
1.3改进粘贴模型——全信息化粘贴DNA计算模型
根据全信息化的DNA粘贴计算内容,将存储区分为3个基本链区:主链区、辅链区和决策链区,其中主链功能是待解问题的数据库,称为输入试管;辅链是根据已知条件建立的“存储库”;而决策链是检测问题的解,如图1所示。主链和辅链是必有,辅链根据具体问题设计,可为多个辅链,决策链根据问题,可有也可能没有,在本文中,决策链则无。

图1 全信息粘贴DNA计算模型的存储链
2 基于地图着色问题改进DNA粘贴算法
2.1地图着色问题
地图中最著名的问题之一,就是四色猜想问题。画一张彩色地图,在相邻的两个不同区域,应当涂上不同颜色。这里的相邻,指的是两个区域有公共边,而不是只有一二个公共点。大量实践证明,一幅地图 最多有4种颜色就够了。
定义1地图着色是指给地图的每个面指定一种颜色,使任意两个有公共边的面颜色不同。若着色时使用了k种颜色,这个着色称为k-着色。
定义2使地图有一个k-着色的最小的k称为地图的色数。
定理1地图问题着色可以转化为图顶点着色问题。
证明将一幅地图转化为为一个无向图,将地图中每一个面记为图中一个顶点。将所有相邻两个面用一条无向边相连,这样可以得到含有顶点和边的平面图G。在这里,假设平面图G有n个顶点,分别记为x1,x2,…,xn,即一个顶点对应一个面。用xi-xj≠0表示顶点xi和另一个顶点xj不能着相同颜色,即表示两个面相邻。在平面图G中,xi和xj有边连接。
显然,地图着色问题可以转化为图顶点着色问题。
2.2地图着色算法
将地图转化为平面图,即求顶点着色问题。先求图的一个最大独立集V1,然后求G-V1的最大独立集V2,再求G-(V1∪V2)的最大独立集V3,如此继续,直到最后求出一个最大独立集Vk,则所需色数ψv(G)=k,即求G的独立数I(G)。由地图四色理论可知,这里k≤4。生物算法如下:
步骤1主链的设计。主链由平面图G的n个顶点x1,x2,…,xn组成。初始时为单链,没有粘贴链。
步骤2辅链的设计。在辅链上直接将图的顶点相邻关系粘贴上去。若图中顶点xi和xj相邻,则在辅链上对应的位段设置为单链,否则设为双链。
步骤3寻找图G的一个最大独立集V1。
步骤4求G-V1的最大独立集V2,依次类推,可以得到剩余顶点集中的最大独立集。得到的独立集个数即是地图的着色数。
3 实 例
以下通过一个实例来详细说明上述算法。
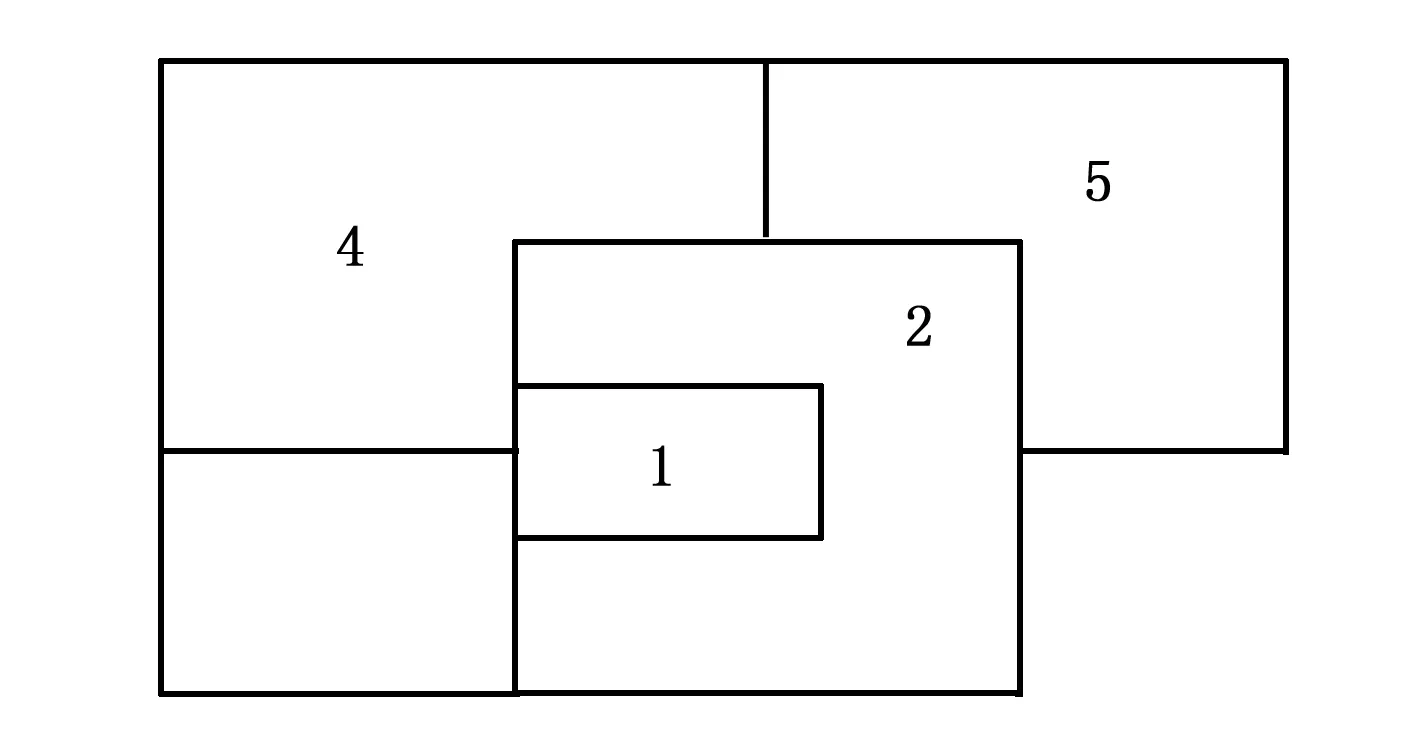
图2 一幅地图
如图2所示,将1,2,3,4,5各个不同的地区分别标记为x1,x2,x3,x4,x5,则可以得到以下的约束条件(1):
x1-x2≠0,x1-x3≠0,x1-x4≠0,x2-x3≠0,x2-x4≠0,x2-x5≠0,x3-x4≠0,x4-x5≠0。
这个地图k-着色问题可以转化为如图3的一个无向图的k-着色问题,即找出满足(1)式条件的解。由定理可知,图2可以转化为平面3的平面图。

图3 图2的平面图表示
图3中的顶点代表图2中的区域。问题转化为求图顶点着色。解决此问题的关键是粘贴模型的建立,步骤如下:
步骤1主链的设计。主链由图的顶点序列x1,x2,x3,x4,x5构成;辅链由顶点xixj的相邻关系组成,这些相邻关系确定了图的全部信息。
步骤2粘贴链的设计。和以往粘贴计算不同的是,在辅链上直接将图顶点相邻关系粘贴上去。若图中顶点xi和xj相邻,则在辅链上对应的位段设置为单链;否则设为双链,如图4所示。
把这个含有主链、辅链和粘贴链的试管称为初始试管,记为T0。复制一个与T0相同的试管,记为T0′。T0′称为备用试管,在步骤4使用。
步骤3寻找图G的一个最大独立集V1。具体步骤如下:
(1)从图G的顶点集V={x1,x2,x3,x4,x5}中随机选取l≥2个顶点子集。为了具有一般性,假设为xi1,xi2,…,xil;复制一个与T0相同的试管,并从中删除辅链中位段xixj,其中xixj或j∉{i1,i2,…,il}或i,j∉{i1,i2,…,il},并将操作后的试管仍记为T0。如在图4中,设l=3,假设所取的顶点为x1,x2,x5,则应从辅链中删除位段为x1x3,x1x4,x2x3,x2x4,x3x4,x3x5,x4x5。若l=2,假设选取的顶点为x1,x5,则应从辅链中删除位段除x1,x5的所有位段。
(2)在主链上并行对l个顶点所对应的主链并行实施设置操作:Set(T0,xi1,xi2,…,xil)。于是,假设对顶点子集{x1,x2,x5}和顶点子集{x1,x5}实施设置操作,操作后所得的试管仍记为T0。
对顶点子集{x1,x2,x5}所实施步骤(1)(2)操作后得存储合成物如图5(a)所示,操作后所得的试管仍记为T0。图5(a)中得到的试管混合物{x1,x2,x5}用二进制数可以表示为11001,而试管混合物图5(b)中得到的试管混合物{x1,x5}可以表示为10001。

图5 辅链和主链实施设置操作后的示意图
(3)检测所得到的解是否是所求问题的解。对试管T0中的存储链并行实施分离操作,通过设计探针来实现。即对于试管T0和顶点xi1,xi2,…,xil实施+(T0,xixj)和-(T0,xixj),其中i,j∈{i1,i2,…,il}且i≠j,若试管T0中的辅链全为双链,则{xi1,xi2,…,xil}是图G的一个独立集,否则不是图G的一个独立集。

图6 删除最大独立集后试管中初始链
(4)对l(2≤l≤n)从大到小逐一进行操作,当第一个非空的子集出现时,这个非空集合{xi1,xi2,…,xil}就是图G的一个最大独立集。本例子中解出一个最大独立集为{x1,x5}。
步骤4求G-V1的最大独立集V2。T0′试管中删除步骤3中最大独立集包含的位段,即在主链和辅链中删除含有x1,x5的位点,试管仍记为T0。T0中初始链的设计如图6所示。
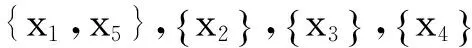
4 结束语
粘贴模型的优点是运算过程中一般不需要DNA链的延伸,不需要酶的参与,而且材科重复使用。本文是采用改进的全信息化的粘贴DNA计算模型,生物操作并行处理,理论上可以实现。
[1]AdlemanLM.MolecularComputationofSolutionstoCombinatorialproblems[J].Science,1994,266(11):1021-1023
[2]Roweis S,Winfree E,Burgoyne R,et al.A sticker-based model for DNA computation[J]. Journal of Computational Biology,1998,5(4):615-629
[3]范月科,强小利,许进.图的最大团与最大独立集粘贴DNA计算模型[J].计算机学报,2010,33(2):305-310
[4]许进,董亚非,魏小鹏,等.粘贴DNA计算机模型(I):理论[J].科学通报,2004,49(3):205-212
[5]许进,董亚非,魏小鹏.粘贴DNA计算和模型(II):应用[J].科学通报,2004,49(3):299-307
[6]王丽娜,仲国强.基于生物芯片技术的地图四着色问题的DNA算法[J].湖北师范学院学报:自然科学版, 2008, 28(2):26-30
[7]马季兰,杨玉星.基于粘贴模型的图顶点着色问题的DNA算法[J].计算机应用,2006,26(12):2998-3000
[8]聂晓艳,耿俊,汤建钢. 图的最小顶点覆盖的粘贴DNA计算模型[J].首都师范大学学报:自然科学版,2013,34(1):8-12
[9]吴雪,宋晨阳,张阳,等.最大匹配问题的粘贴DNA算法[J].计算机科学,2013,40(12):127-140
[10]张勋才,牛莹,郗方.基于微流控技术图顶点着色问题的DNA计算模型[J].吉林大学学报学:工学版,2013,43(1):206-211
(责任编辑:汪材印)
10.3969/j.issn.1673-2006.2016.10.028
2016-07-11
安徽省自然科学基金项目(1608085QF149)。
马莹(1981-),女,安徽灵璧人,硕士,讲师,主要研究方向:图论、DNA计算。
TP301
A
1673-2006(2016)10-0110-04
