线状李超代数Ln,m上的Yang-Baxter方程
2016-11-11杨勇刘文德
杨勇,刘文德
(哈尔滨师范大学数学科学学院,黑龙江 哈尔滨 150025)
线状李超代数Ln,m上的Yang-Baxter方程
杨勇,刘文德
(哈尔滨师范大学数学科学学院,黑龙江 哈尔滨150025)
在特征零的代数闭域上,首先做出Ln,m的一个空间的直和分解,从而将Ln,m上的Yang-Baxter方程的解分为若干情形.然后分别在每种情形下对Yang-Baxter方程进行求解,进而得到了Ln,m上的所有的Yang-Baxter方程的解的矩阵形式.
Yang-Baxter方程;幂零李超代数;线状李超代数
1 引言
1960年,Baxter在研究波动理论的积分方程时,提出了Rota-Baxter代数的概念[1].这一理论在数学与物理的许多领域得到了广泛的应用.在李代数与李超代数上,权0的Rota-Baxter算子即为经典的Yang-Baxter方程的解,权1的Rota-Baxter算子即为变形的Yang-Baxter方程的解.近年来,许多学者刻画了低维代数上的Rota-Baxter算子.例如,文献[2]证明了有限维实可除代数上的Rota-Baxter算子都是平凡的,文献[3]计算了线状李超代数L1,2上的Yang-Baxter方程的解,文献[4]刻画了有限维Hamilton代数上的Rota-Baxter算子.由于其丰富的应用价值,Yang-Baxter方程的研究成为了一个重要的研究课题.
1970年,Vergne在研究幂零李代数簇的可约性时,提出了线状李代数的概念并且指出任何一个线状李代数都可由线状李代数Ln的形变得到[5].类似于李代数的情形,任何一个线状李超代数都可由线状李超代数Ln,m的形变得到.线状李超代数作为一类特殊的幂零李代数,其研究成为了许多学者关注的重要课题.例如,文献[6]对低维的线状李超代数进行了分类,文献[7]计算了线状李超代数Ln,m的导子及保积Hom-结构,文献[8]刻画了线状李超代数Ln,m的极小忠实表示,文献[9]给出了线状李超代数Ln,m的无穷小形变.本文在特征零的代数闭域上,首先做出Ln,m的一个空间的直和分解,从而将Ln,m上的Yang-Baxter方程的解分为若干情形.然后分别在每种情形下对Yang-Baxter方程进行求解,进而得到了Ln,m上的所有的Yang-Baxter方程的解的矩阵形式.
2 基本概念和引理
定义2.1[9]设G是一个幂零李超代数,若存在正整数p,q,使得
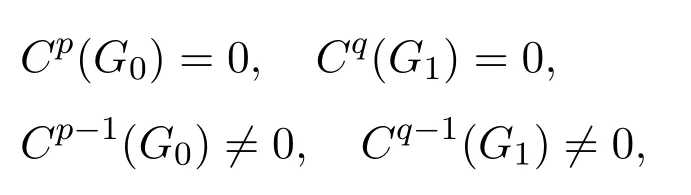
其中

则称(p,q)为李超代数G的超幂零指数.
定义2.2[9]设是一个幂零李超代数,其中dim G0=n,dim G1=m,如果G的超幂零指数为(n-1,m),则称G为线状李超代数.
定义2.3设R是李超代数G上的一个齐次的线性算子,如果对任意的x,y∈G,有
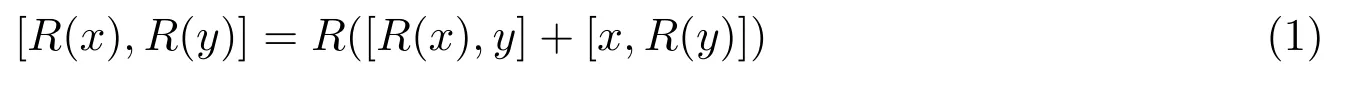
则称R是李超代数G上的Yang-Baxter方程的解.
3 主要结果及证明
本文约定F为特征零的代数闭域,设{X0,X1,···,Xn|Xn+1,···,Xn+m}是线状李超代数F=Ln,m的标准基,其非零乘法为:[X0,Xi]=Xi+1,i∈{1,···,n-1,n+1,···,n+m-1}.
设F上的Yang-Baxter方程的解R在该组基下的矩阵是(aij),则有
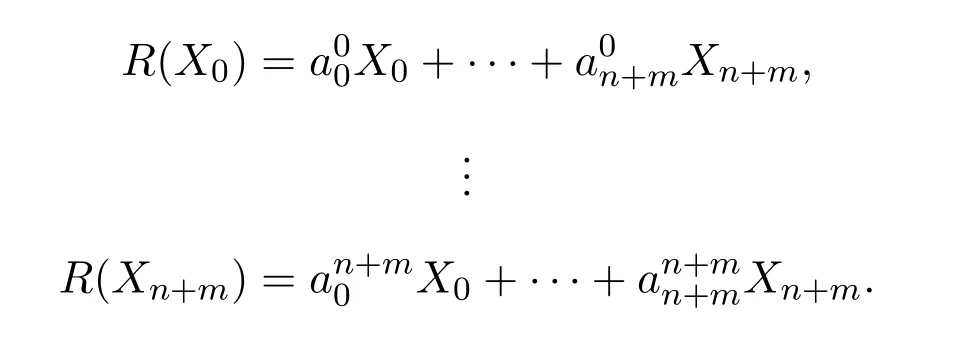
令V0=span{X1,···,Xn},V1=span{Xn+1,···,Xn+m}.
引理3.1设R是F上的线性算子,则对于任意的x,y∈F,有


引理3.2设R是F上的齐次的线性算子,则有以下两个结论成立:
(1)若R是F上的偶的Yang-Baxter方程的解,则R(X2),···,R(Xn)∈V0.
(2)若R是F上的奇的Yang-Baxter方程的解,则R(Xn+2),···,R(Xn+m)∈V0.

引理3.3设R是F上的偶的线性算子,则有以下两个结论成立:


引理3.4设R是F上的奇的线性算子,则有以下两个结论成立:

证明此定理的证明,可仿照引理3.3的证明得到.
以下表达式中的x,y,αi,βj表示F上的任意元素,α表示F上的任意非零元素,∗表示F上的任意元素或相应阶数的任意矩阵.
定理3.1设R是F上的偶的线性算子,则R是Yang-Baxter方程的解当且仅当R在标准基下的矩阵为以下两类矩阵之一:
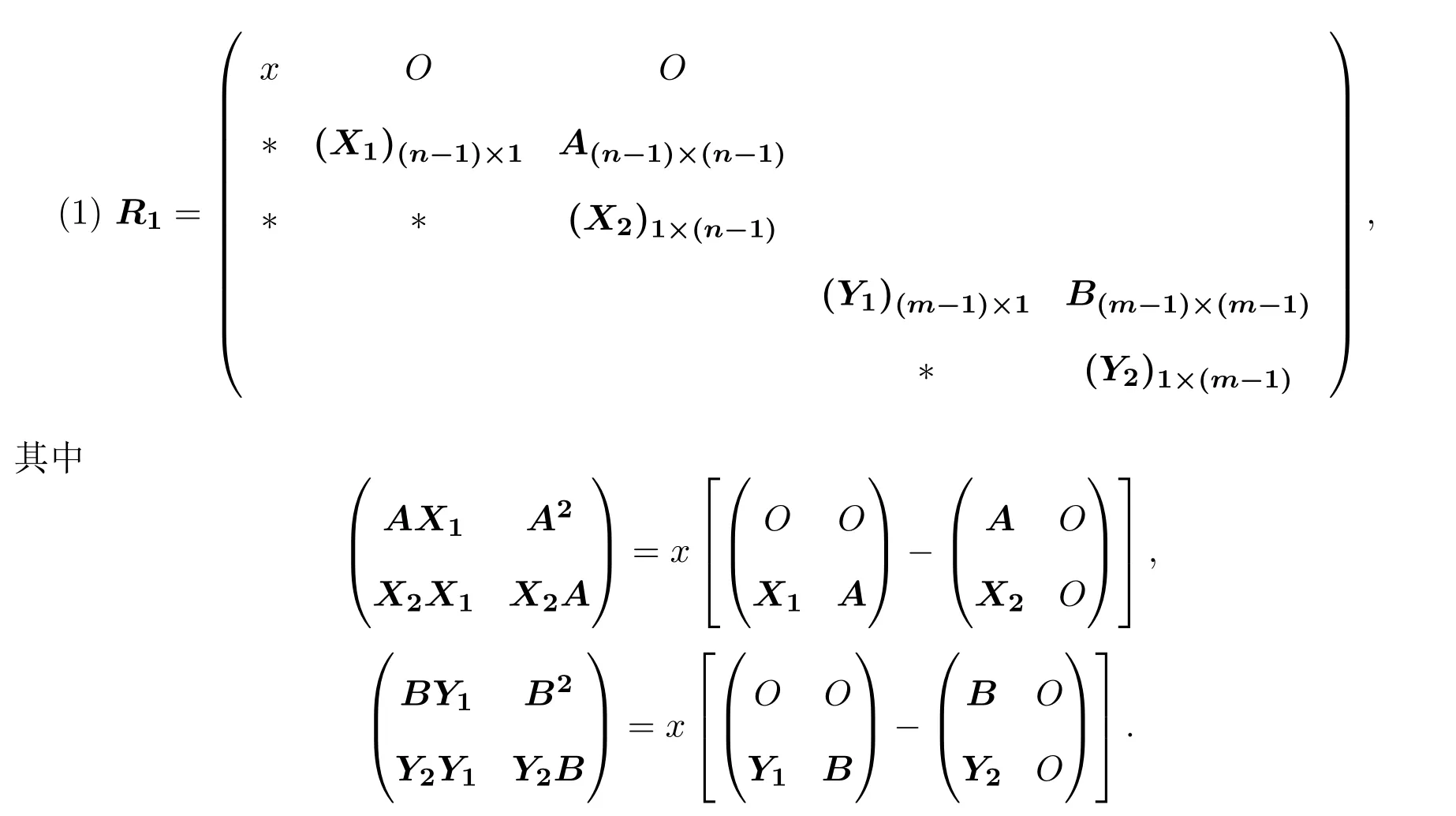
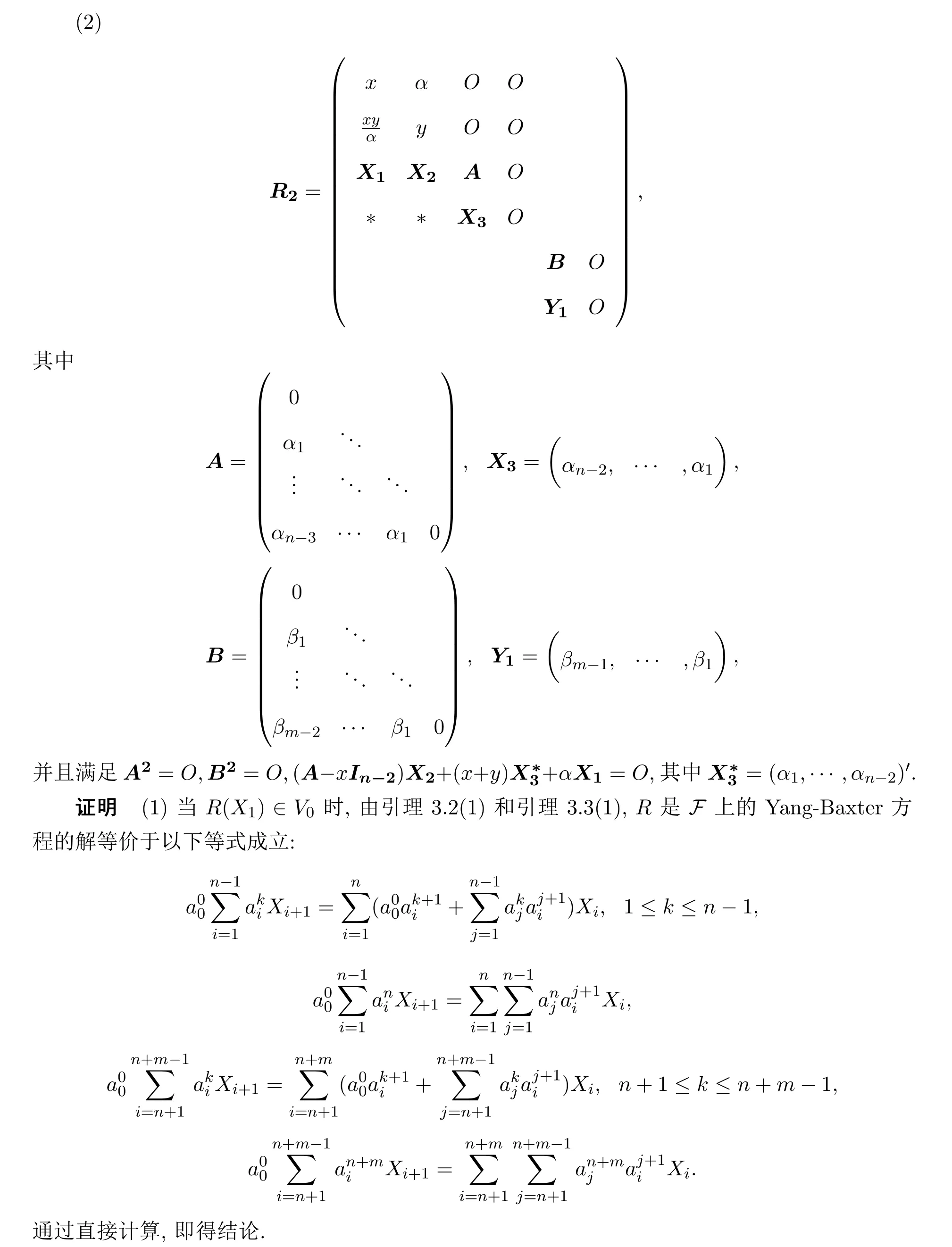

定理3.2设R是F上的奇的线性算子,若R(Xn+1)∈V0,则R是F上的Yang-Baxter方程的解当且仅当R在标准基下的矩阵为以下矩阵:

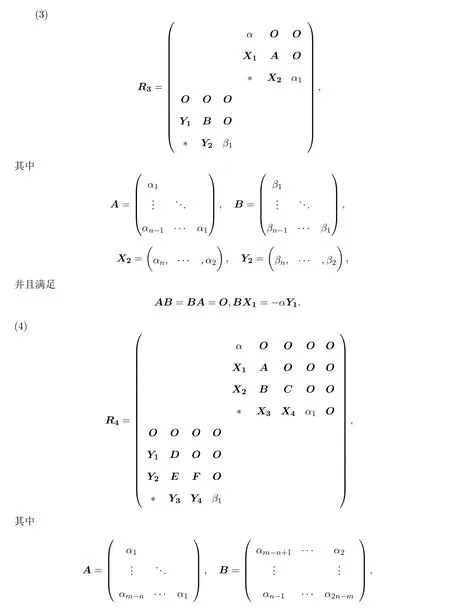
定理3.3设R是F上的奇的线性算子,若R(Xn+1)/∈V0,则R是F上的Yang-Baxter方程的解当且仅当R在标准基下的矩阵为以下五类矩阵之一:




[1]Baxter G.An analytic problem whose solution follows from a simple algebraic identity[J].Pacific J.Math.,1960(10):731-742.
[2]陈美微,刘文德.有限维实可除代数的Rota-Baxter算子[J].数学的实践与认识,2013,43(16):243-247.
[3]焦阳,刘文德.Filiform李超代数L1,2上的Yang-Baxter方程[J].数学的实践与认识,2014,44(17):283-287.
[4]温雅慧,刘文德.有限维Hamilton代数上的Rota-Baxter算子[J].数学的实践与认识,2013,43(23):262-267.
[5]Vergne M.Cohomologie des algèbres de Lie nilpotentes.Apllicationà l'étude de la variété des algèbres de Lie nilpotentes[J].(French)Bull.Soc.Math.France 1970(98):81-116.
[6]Gilg M.Low-dimensional filiform Lie superalgebras[J].Rev.Mat.Complut.,2001(14):463-478.
[7]焦阳,刘文德.Filiform李超代数Ln,m的导子和保积Hom-结构[J].纯粹数学与应用数学,2014,30(5):534-543.
[8]Wang Q.Chen H,Liu W.On representations of the Filiform Lie superalgebras Ln,m[J].J.Geom.Phys.,2015(97):93-104.
[9]Khakimdjanov Y,Navarro R M.A complete description of all the infinitesimal deformations of the Lie superalgebras Ln,m[J].J.Geom.Phys.,2010(60):131-141.
2010 MSC:16T25
The Yang-Baxter equation of the filiform Lie superalgebras Ln,m
Yang Yong,Liu Wende
(School of Mathematical Sciences,Harbin Normal University,Harbin150025)
At first,we make a space direct sum decomposition of Ln,mover an algebraically closed field of characteristic zero,so the solutions of the Yang-Baxter equation of the filiform Lie superalgebras Ln,mwere divided into several situations.We solve the Yang-Baxter equation in each case,then we obtain all the solutions of the Yang-Baxter equation of the filiform Lie superalgebras Ln,min terms of the matrix form.
Yang-Baxter equation,nilpotent Lie superalgebra,filiform Lie superalgebra
O152.5
A
1008-5513(2016)05-0536-10
10.3969/j.issn.1008-5513.2016.05.010
2016-04-05.
国家自然科学基金(11471090,11501151);省自然科学基金(A2015003).
杨勇(1992-),硕士生,研究方向:李代数与李超代数.
刘文德(1965-),博士,教授,研究方向:李代数与李超代数.
