台湾凤梨释迦果实生长发育的数学模型研究

蔡小林，潘介春，周煜棉，刘红红，黄桂香

(广西大学农学院，广西南宁 530004)



台湾凤梨释迦果实生长发育的数学模型研究

蔡小林，潘介春*，周煜棉，刘红红，黄桂香

(广西大学农学院，广西南宁 530004)

[目的]确定凤梨释迦合理的栽培管理时期，建立该品种果实生长发育的数学模型。[方法]通过测定凤梨释迦果实生长发育期间果实纵径、横径、果柄长度和果柄粗度，建立凤梨释迦果实生长发育模型。[结果]授粉28 d后，凤梨释迦果实的纵径、横径存在一个迅速生长期，期间果实纵径发育速度明显快于横径，而果柄在此期间加粗生长和伸长生长也呈快速增长趋势；授粉56 d后果实发育和果柄生长均进入缓慢生长期。果实与果柄发育存在同步性，且各指标相关系数达0.980 00以上，各指标与授粉后天数之间回归方程相关系数达0.970 00以上。[结论]台湾凤梨释迦果实横径、纵径、果柄长和果柄粗与授粉后发育天数之间存在明显的多项式回归关系，且其生长进程数学模型同为三次方程。该数学模型拟合良好，能够较好地反映果实和果柄的生长发育动态变化。

凤梨释迦；果实；生长发育；数学模型

凤梨释迦(Atemoya)为冷子番荔枝(Annonacherimolia)与 普通番荔枝(A.squamosa)的杂交种，又称阿莫蒂耶番荔枝，为番荔枝科(Annonaceae)番荔枝属(Annona)多年生半落叶性灌木或小乔木，与芒果、荔枝、菠萝、山竹子同列为世界五大热带名果，是番荔枝属中品质最佳的一种果品[1-2]。目前，凤梨释迦在漳州、浙北地区、广西崇左等地进行了引种栽培，并对其生物学特性、引种栽培表现及栽培技术进行了研究[3-8]。但关于凤梨释迦果实生长发育动态变化鲜见报道。笔者通过测定凤梨释迦果实横纵径、果柄长和粗度建立其果实生长发育的数学模型，以期为凤梨释迦科学管理、合理施肥提供理论依据。

1　材料与方法

1.1试验地概况试验于2015年10月～2016年3月在广西大学农学院果树标本园进行。该果园土壤为黏性红壤土，土壤肥力中等，管理水平一般。

1.2试验材料供试品种为10年生凤梨释迦番荔枝，株行距4.0 m×5.0 m，南北行向，冠幅3.5 m×4.5 m，株高(3.0±0.1)m，干径(10.0±0.5)cm。

1.3试验方法选择4株生长健壮、树势一致的凤梨释迦番荔枝，于10月10日统一人工授粉，授粉后第7天在每株树随机选取10个生长正常的幼果进行挂牌标记，共40个果实，每隔7 d用数显游标卡尺测定果实纵横径及果柄粗度，用直尺测定果柄长，直至果实成熟或各项指标不再变化。

1.4数据处理运用 WPS Excel进行数据分析。

2　结果与分析

2.1果实纵横径生长动态变化由图1、2可知，凤梨释迦果实整个发育过程中，纵径生长量始终大于横径，表现为纵向生长。授粉前28 d，果实纵横径生长较为缓慢，净生长量相差较小；授粉后28～56 d，果实纵横径快速生长，净生长量明显增加，且在授粉后49 d达净生长量高峰，平均日净增长量0.149 cm；授粉后56 d至果实成熟，果实生长趋于缓和，纵横径净生长量基本一致。由此可知，凤梨释迦果实整个生长期可分为3个阶段：缓慢生长(幼果期)、快速生长(膨大期)、缓慢生长(成熟期)。

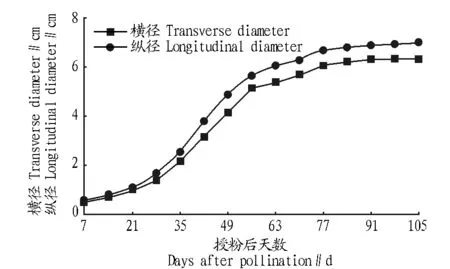
图1　果实纵横径变化Fig.1　Change of longitudinal and transverse diameters of fruit

图2　果实净生长量变化Fig.2　Changes of net growth of fruit stalk

2.2果实果形指数变化由图3可知，果形指数在整个果实发育过程中先上升后下降。前期由于果实纵径生长速度快于横径，表现果形指数随发育天数增加而不断增加，授粉35 d后，果实横径生长速度略有增加，果形指数下降，成熟期果形指数为1.11，呈长圆形。

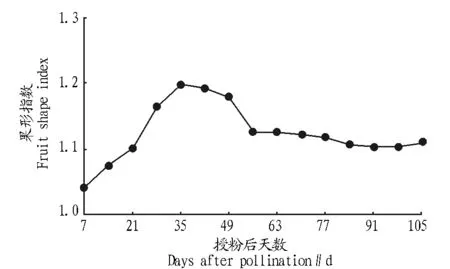
图3　果形指数变化Fig.3　Changes of fruit shape index

图4　果柄生长发育指标变化Fig.4　Change of fruit stem growth and development index

2.3果柄生长发育动态分析由图4、5可知，在整个果实发育过程中，相对果实纵横径生长而言，果柄生长变化较为缓和，果柄长和果柄粗在授粉35～42 d均表现为快速生长趋势，在42 d净生长量出现峰值，果柄长、果柄粗日净生长量分别为0.84、0.91 mm，这与果实生长发育表现出同步性。凤梨释迦果实成熟期果柄长达2.91 cm，果柄粗达0.61 cm。

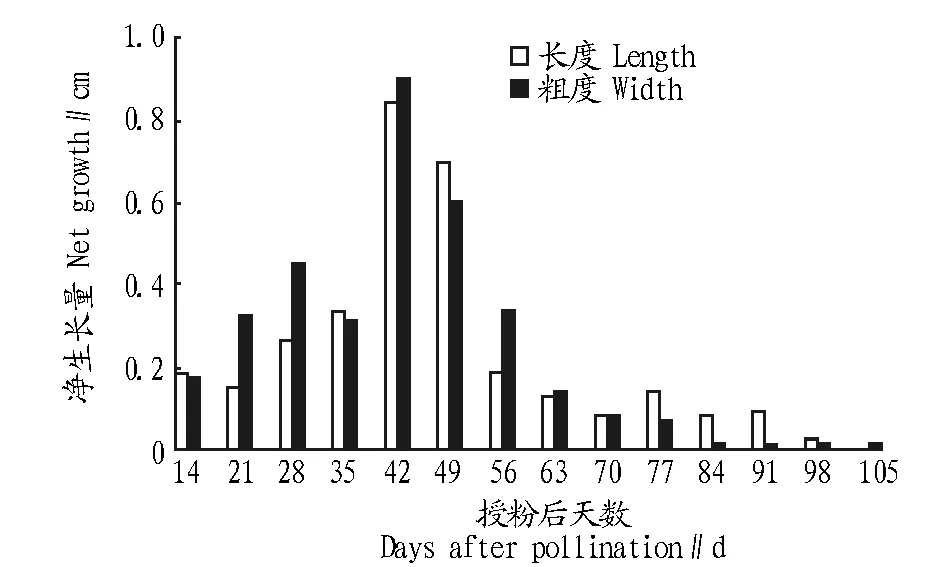
图5　果柄净生长量变化Fig.5　Change of fruit stem net growth

2.4果实与果柄生长发育相关性分析由表1可知，果实的横径、纵径、果柄长、果柄粗两两之间均呈正相关，且相关系数均达极显著水平(P<0.01)，说明凤梨释迦果实各项生长指标间相关程度较高。

表1　果实与果柄各指标相关性

注：**表示极显著相关(P<0.01)。

Note:** indicated extremely significant correlation (P<0.01).

2.5果实生长发育模型的建立根据表2建立了凤梨释迦果实授粉后天数(X)与果实横径、纵径、果柄长和果柄粗4个指标(Y)的关系方程。果实纵径、横径和果柄长、果柄粗发育均为三次多项式方程，其中，果实纵径、横径发育方程决定系数分别为0.986 66、0.983 98，果柄长、果柄粗发育方程决定系数分别为0.971 82、0.974 00，均表现出较高的拟合精度。

表2果实授粉后天数与果实生长发育指标的关系

Table 2Correlation between the fruit development and growth index and the pollination days

指标Index回归方程式Regressionequation相关系数Correlationcoefficient横径TransversediameterY=-0.00002X3+0.00205X2+0.01246X+0.088730.98666纵径LongitudinaldiameterY=-0.00002X3+0.00186X2+0.03822X-0.161690.98398果柄长FruitstemlengthY=-0.0000006X3+0.00006X2+0.0034X+2.54930.97182果柄粗FruitstemwidthY=-0.0000007X3+0.00007X2+0.00349X+0.240760.97400

3　结论与讨论

研究结果表明，凤梨释迦果实的生长发育进程具有明显的规律性，果实纵横径生长动态曲线近似“S”形。果实生长高峰期主要是28～56 d，即果实膨大期，此期是凤梨释迦果实产量和品质形成的关键时期。因此，为充分满足凤梨释迦果实生长发育的需要，生产上应根据果实生长发育规律采取相应的栽培技术措施，如水肥管理和喷施植物生长调节剂等。

果柄生长发育与果实发育存在密切关系。张大鹏[9]研究发现，荔枝落果果柄各组织、细胞的数量和分化速度均不及坐果果柄。陈小明[10]研究发现，梨果形偏斜度与果柄长度呈正相关，与果柄粗度呈负相关，即果柄越长，斜果、畸形果发生比率越大；果柄越粗，斜果、畸形果发生比率越小。该试验仅调查了凤梨释迦果实果柄的生长发育动态，结果发现，果柄的生长与果实纵横径的生长表现出同步性，呈近“S”型曲线，在授粉56 d后生长非常缓慢。果柄的粗壮为果实水分和营养的输送提供了基础，这也是番荔枝果实几乎不出现落果现象的原因之一。相关性分析表明，果实横径、纵径与果柄长、果柄粗相关性均在0.980 00以上，达极显著水平，因此，生产上可依据果柄的生长发育变化间接获取果实发育动态，避免果实调查过程中造成果面划痕而导致锈斑，影响其商品品质，也可在果实套袋栽培过程中通过测定果柄生长而快速了解果实发育动态，减少解封果袋的次数。

果实生长发育数学模型的建立有助于科学地预测和掌握果实在不同时期的发育水平，为科学管理提供理论依据[11]。该研究结果表明，凤梨释迦果实纵横径、果柄长及果柄粗与授粉后发育天数为三次方程，相关系数R2在0.970 00以上，该数学模型拟合良好，能够较好地反映果实和果柄的生长发育动态变化。但该模型仅对果实纵横径、果柄长及果柄粗与授粉后发育天数之间的关系进行了研究，而未将果实鲜重、干重等及果实内在品质联系起来，有待进一步探索。

[1] 潘悦.台湾释迦的离体培养与植株再生[J].福建热作科技，2009(1)：5-6.

[2] 李良.最甜的水果：台湾释迦[J].生态文化，2011(1)：38.

[3] 李丽容，郑陈婷，祝秋萍，等.凤梨释迦生物学特性及其在漳州的种植区划[J].福建热作科技，2012(1)：45-48.

[4] 方仁，尧金燕，白先进，等.凤梨释迦在广西崇左的引种表现及其栽培技术[J].中国南方果树，2015(4)：119-121.

[5] 韩明丽，邱坤财，张乐，等.凤梨释迦在浙北地区引种表现及栽培技术[J].浙江农业科学，2013(3)：287-289.

[6] 陈桂平，曾少敏，廖玉章，等.台湾凤梨‘释迦’引种表现及主要栽培技术[J].中国园艺文摘，2011(9)：176-178.

[7] 李甘来.凤梨释迦生物学特性及高产栽培技术[J].福建农业，2011(10)：12-13.

[8] 曾少敏.台湾凤梨释迦栽培技术[J].科学种养，2008(5)：20-21.

[9] 张大鹏.荔枝果柄结构发育与落果的关系[J].园艺学报，1997(2)：2-7.

[10] 陈小明.梨果形偏斜因子研究[D].北京：中国农业科学院，2010.

[11] 李慧峰，李林光，张琮，等.苹果果实生长发育数学模型研究[J].江西农业学报，2008(4)：40-42.

Mathematic Model of Fruit Growth and Development of Atemoya cv. Tai Wan(AnnonasquamosaL.)

CAI Xiao-lin, PAN Jie-chun*, ZHOU Yu-mian et al

(College of Agronomy, Guangxi University, Nanning, Guangxi 530004)

[Objective] To determine the reasonable cultivation period for atemoya, and to establish the mathematical model of the growth of fruits of this variety. [Method] We detected the fruit longitudinal diameter, transverse diameter, fruit stalk length and width during the fruit growth and development of atemoya, and to establish the fruit growth model of atemoya. [Result] Atemoya fruit transverse diameter and longitudinal diameter had a growth peak on 28 days after pollination. Fruit diameter growth rate was significantly faster than the transverse diameter during the period of rapid growth. Fruit stalk width growth and elongation growth during this period also showed a rapid growth trend. Fruit size and Fruit stalk growth were both at a slow growth period on 56 d after pollination. Synchronization growth was observed for fruit and fruit stalk development. The correlation coefficient of each index was greater than 0.980 00. The regression equation of the correlation coefficient between day number after pollination and each index was greater than 0.970 00. [Conclusion] There are obvious polynomial regression relations among atemoya fruit transverse and longitudinal diameters, stalk length, stalk width and growth days after pollination, and the mathematical model of the growth process is also a cubic equation. This mathematic model has good fitting, and can better reflect the dynamic changes of fruit and stalk development.

Atemoya; Fruit; Growth and development; Mathematical model

广西自然科学基金项目“东盟热带亚热带特色果树品种资源引进选育研究”(桂科14123001-1-3)。

蔡小林(1991- )，男，湖南攸市人，硕士研究生，研究方向：果树栽培与生理。*通讯作者，副教授，硕士，硕士生导师，从事果树栽培生理及育种工作。

2016-07-13

S 667.9

A

0517-6611(2016)27-0044-02