在课堂中探索交流，促进知识生成生长——“勾股定理”教学有感

王　新

（北京市通州区玉桥中学）

在课堂中探索交流，促进知识生成生长——“勾股定理”教学有感

王新

（北京市通州区玉桥中学）

新课程倡导：“数学学习的过程应该是一个探索与交流的过程——在探索的过程中形成自己对数学的理解，并在与他人的交流过程中逐步完善自己的想法。”教师不应是知识的独裁者，而应是学生探究学习的合作伙伴，教学中要为学生搭建探究、交流的平台，使知识自然生成、自然生长。笔者以“勾股定理”教学为例，谈一下自己在教学中的做法与思考。

一、让知识在课堂中动态生成

建构主义强调，学习者并不是空着脑袋进入学习情境中的。在日常生活和以往各种形式的学习中，他们已经形成了有关的知识经验，他们对任何事情都有自己的看法。即使是有些问题他们从来没有接触过，没有现成的经验可以借鉴，但是当问题呈现在他们面前时，他们还是会基于以往的经验，依靠他们的认知能力，形成对问题的解释，提出他们的假设。

教学的核心理念是一切为了每一个学生的发展。这个发展是一个动态的生成过程，就教学知识本身而言只是一个结论，而每个数学知识的发生与发展都是一个动态生成的过程，课堂教学中教师应该精心设计，将这个动态过程展现在学生面前，让他们亲身经历，经历知识的发生、发展与形成过程，让他们真实感受知识的内涵与外延。

如，在“勾股定理”新授课教学中，我并没有直接将知识结论生硬地搬上课堂，而是首先以学生小时候常做的折纸游戏入手（如图1），引导学生思考：折叠起的四个等腰直角三角形的边长与原正方形边长之间的关系，并不断变化外部正方形的边长，使学生在不断变化的数据中去探究不变的本质特点。与此同时，请同学们动手用圆规和刻度尺画出直角三角形，使它们的直角边分别为以下数据（学生分组完成）

图1

（1）3厘米，4厘米；（2）6厘米，8厘米；（3）5厘米，12厘米

再次引导学生思考：所做直角三角形的三边间的数量关系？并通过几何画板做演示，使学生在折纸、画图、测量、计算的过程中感受知识的合情合理，进而从情感上接受知识。

二、让课堂成为学生展示的舞台

教学不是知识的传递，而是知识的处理和转换。教师不单是知识的呈现者，也不应该是知识权威的象征，而应该重视学生自己对各种现象的理解，倾听他们时下的看法，引导学生丰富或调整自己的解释。

如，在对勾股定理进行论证的教学环节中，我事先让学生自学、查询有关定理的由来与证明方法，做好预习准备工作，并告诫他们上课时我会让准备充分的学生上台展示。说实在的，当时只是想让他们简单预习一下，没想到第二天他们在课堂上的表现令我惊讶不已，他们准备之充分、积极性之高是我未曾遇见过的，他们有的做好了教学PPT，有的将证明过程用彩笔写在了大的挂历纸上。课堂上，他们各小组讨论热烈；回答问题，积极主动；讲台展示，争先恐后，表现力极强，其中有些方法既简单又易理解。

展示如下：

∴a2+2ab+b2=c2+2ab

∴a2+b2=c2

图2　

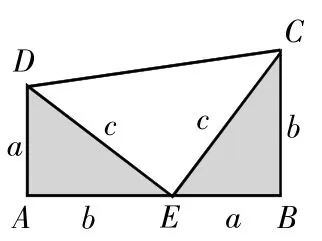
图3

方法二：以a、b为直角边，以c为斜边作了两个全等的直角三角形，就可以得到每个直角三角形的面积都是把这两个直角三角形拼成图中的形状，使A、E、B三点在一条直线上。利用梯形ABCD的面积等于得到

方法四：如图5，边长为c的正方形，由四个全等的直角三角形和一个小正方形组成其面积为c2亦可加以证明。

图4　

图5

……

课堂上他们的证法得到认可时的欣喜、自豪的神态至今给我留下了深刻的印象。

我们不可否认，每个学生都是具有丰富思想的个体，他们对知识的接受与理解的途径和程度也不相同，课堂教学中应尽量让学生将他们所知、所做、所感、所悟尽情地表达出来，不要用教师的思维代替学生的思维，不要用书本中的语言代替学生的语言，更不能独占课堂领地。

三、让课堂成为师生成长的圣地

从古到今，“教学相长”一直是我们所追求的教育境界。所谓“教学相长”，是指“教与学两方面互相影响和促进，教与学相互依存、相互推动，相辅相成、相得益彰”。这种观点实质上就是说“课堂应是师生共同成长、提高的场所”。自然界中每一个生命都离不开成长的空间和精心的呵护，教学亦是如此。好的课堂、精彩的课堂应该是活跃的、动态的，是知识与思维之间相互碰撞的，是师生之间、生生之间相互交流、共同探索的过程，是一种生命感染生命、激情点燃激情的过程。

在勾股定理探究学习的过程中，得到提高的不仅是学生，还有我这个具有多年教学经验的教师，学生的课堂表现进一步冲击着我的教学观，他们用实际行动在告诉我“我们才是课堂的主人”“要相信我们能行”。他们的表现督促我要不断提升自身专业素养，教师的站位决定学生的高度，教师的素养决定学生的素养，正如加德纳指出的那样“每个人都是一个自我完善的过程”，教师也一样，需要自我完善、自我建构、自我反思、自我提高。教师在学生的成长中发展，学生在教师的发展中成长，我认为这才是真正意义上的教学相长。

因此，教学过程中教师应遵循教育教学规律，认真挖掘教材知识本身的特点，并将其与学生已有的生活经验相结合，将枯燥的数学知识转变为探究性问题，让学生在动手、动脑的探究活动中感受知识的发生与发展，感受作为数学家的成就感、自豪感，感受到数学知识本身独到的美与魅力，从而变“要我学为我要学”，并在不断探索、掌握知识的过程中，获得和提高解决问题的能力。

李道甜.浅谈勾股定理的教学与应用［J］.中学教学参考，2010.

·编辑张珍珍